Use new possibilities of MetaTrader 5
Elastic net regression using coordinate descent in MQL5
MetaTrader 5
—
Examples
| 12 September 2023, 11:02
1 449
0
Introduction
Elastic net regression combines the best qualities of the ridge and lasso techniques to build general linear models. Applying it makes it possible to minimize one of the main disadvantages of regression, overfitting. This is especially relevant to trading strategy development, as it is known, that the most common reason for poor performance or strategy failure.Comes as a result of mistaking noise for patterns during training. In this article we will present the implementation of elastic net regression, that uses the coordinate descent method of optimization in pure MQL5. Towards the end of the article we will demonstrate a practical application of this technique through the development of a simple moving average based predictive strategy.
Regularization
When building predictive models the goal is to create an exemplar that can discern some unique pattern that can be exploited for real world use. To do so effectively we have to ensure that the model is "learning" relevant patterns from the training data. This is obviously easier said than done. What usually happens is that the model ends up picking up on irrelevant information (noise) which ultimately hurts its performance when put to use. Regularization is a process used to minimize the effects of overfitting.
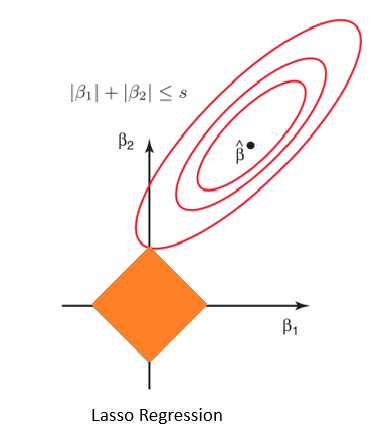
The lasso technique helps reduce training bias by repressing redundant predictors when the model is defined by too many optimizable variables. Thereby simplifying the model.
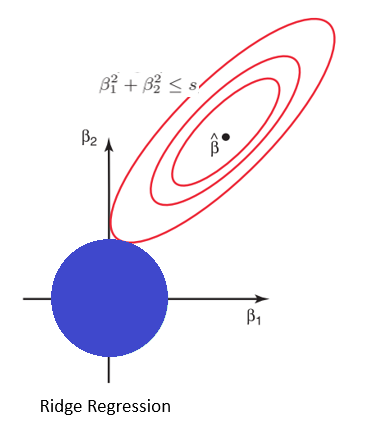
In ridge regression, coefficients of the regression equation are minimized so as to move them away from their optimum. This helps to generalize the model whilst still keeping all the predictors.
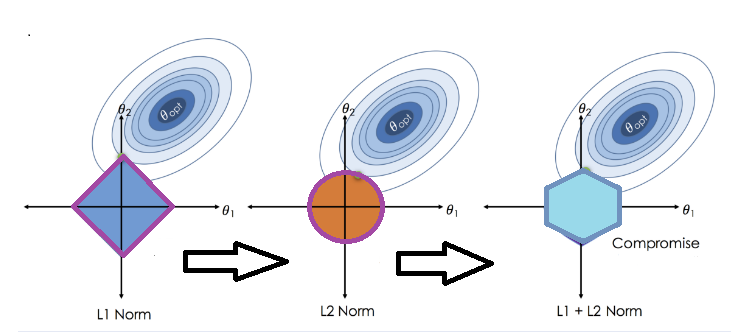
Both the lasso and the ridge are distinguished by the nature of the penalty term applied. The elastic net regression penalty term is a combination of the absolute value and square of the coefficents, weighted by two hyperparameters, alpha and lambda.
This way, alpha controls the type of regularization. When alpha is zero the penalty term reduces to the l2-norm, alternatively, when alpha is 1 the penalty function becomes the l1-norm. Specification of alpha that is between 0 and 1 makes it possible to build linear models that combine the qualities of both ridge and lasso regression to a certain degree as governed by the lambda hyperparameter which controls the degree of regularization.
Such models can be a boon when applied to trading strategy development where we often find ourselves blindly applying numerous predictors in the hope of finding some combination that produces profit. Using elastic net regression we can minimize overfitting whilst also being able to separate useless indicators from those that have significant predictive potential. And we can do this without worrying about how the indicators are related to each other. It almost seems too good to be true.
Coordinate Descent
Coordinate descent is a method of optimization well suited to multivariable optimization. A complex multidimensional optimization problem is reduced into a collection of one dimensional problems. Achieved by iteratively minimizing each of the individual dimensions of a function , whilst keeping the values of the function in other dimensions static. There are numerous resources on the internet that can provide more detailed explanations for those interested. Here, we are interested in its application to strategy development.
For our purposes, the coordinate descent method will be used in two ways in the implementation of elastic net regression. First it will be used to determine the optimal lambda based on a fixed alpha, specified by the user. Once this is done, the optimization method is called again to work on the beta coefficients of the regression equation. Lets dive into some code to see how this is accomplished.
The CCoordinateDescent class
//+------------------------------------------------------------------+ //| Coordinate Descent optimization class | //+------------------------------------------------------------------+ class CCoordinateDescent { private: bool m_initialized; // Was everything legal and allocs successful? double m_beta[]; // Beta coefs (m_nvars of them) double m_explained; // Fraction of variance m_explained by model; computed by Train() double m_xmeans[]; // Mean of each X predictor double m_xscales[]; // And standard deviation double m_ymean; // Intercept (mean of Y) double m_yscale; // Standard deviation of Y int m_nvars ; // Number of variables int m_observs ; // Number of cases bool m_covarupdates ; // Does user want (often faster) covariance update method? int m_nlambda ; // Reserve space for this many m_beta sets for saving by TrainLambda() (may be zero) double m_lambdabeta_matrix[]; // Saved m_beta coefs (m_nlambda sets of m_nvars of them) double m_lambdas[]; // Lambdas tested by TrainLambda() double m_x_matrix[]; // Normalized (mean=0, std=1) X; m_observs by m_nvars double m_y[]; // Normalized (mean=0, std=1) Y double m_resid[]; // Residual double m_xinner_matrix[]; // Nvars square inner product matrix if m_covarupdates double m_yinner[]; // Nvars XY inner product vector if m_covarupdates public: //constructor CCoordinateDescent(const int num_predictors, const int num_observations, const bool use_covariance_updates, const int num_lambdas_to_trial) ; //desctructor ~CCoordinateDescent(void) ; //Accessor methods for private properties double GetYmean(void) { return m_ymean; } double GetYscale(void) { return m_yscale;} double GetExplainedVariance(void) { return m_explained;} double GetXmeansAt(const int index) { if(index>=0 && index<ArraySize(m_xmeans)) return m_xmeans[index]; else return 0;} double GetXscalesAt(const int index) { if(index>=0 && index<ArraySize(m_xscales)) return m_xscales[index]; else return 0;} double GetBetaAt(const int index) { if(index>=0 && index<ArraySize(m_beta)) return m_beta[index]; else return 0;} double GetLambdaAt(const int index) { if(index>=0 && index<ArraySize(m_lambdas)) return m_lambdas[index]; else return 0;} double GetLambdaBetaAt(const int index) { if(index>=0 && index<ArraySize(m_lambdabeta_matrix)) return m_lambdabeta_matrix[index]; else return 0;} double GetLambdaThreshold(const double alpha) ; //Set model parameters and raw input data bool SetData(const int begin, const int num_observations, double &xx_matrix[], double &yy[]) ; //Training routines void Train(const double alpha, const double lambda, const int maxits, const double convergence_criterion, const bool fast_test, const bool warm_start) ; void TrainLambda(const double alpha, const int maxits, const double convergence_criterion, const bool fast_test, const double maxlambda, const bool print_steps) ; } ;
The CCoordinateDescent class is defined in the CoordinateDescent.mqh file. Its constructor is parametric and is used to specify important features of a model, but before we get into this, there are some pertinent issues about a specific data construct to be used.
The library we will specify will not use any unique data types, such as the new matrix and vector types of MQL5. This is to ensure compatibility with mql4. Since there is no way to dynamically define multidimensional arrays, matrices will be represented as regular flat arrays. An example is the best way to illustrate the construct.
Supose we want to define a matrix with 4 rows and 3 columns. We would create an array of size 4 multiplied by 3 , ie 12. The members of this array will be arranged as they would appear if using the built in matrix data type. That is to say, using our example, the first row members are specified first, then the second row members, and so on. The code snippet below illustrates the creation of a 4 by 3 matrix , where the each value in a column is the same.
int rows=4, columns=3; double our_matrix[]; ArrayResize(our_matrix,rows*columns); /* Creating matrix with columns of 1s,2s,3s */ for(int i = 0; i<rows; i++) for(int j=0; j<columns; j++) our_matrix[i*columns+j]=j+1; ArrayPrint(our_matrix);
Output from ArrayPrint.
KP 0 13:01:32.445 Construct(GBPUSD,D1) 1.00000 2.00000 3.00000 1.00000 2.00000 3.00000 1.00000 2.00000 3.00000 1.00000 2.00000 3.00000
When traversing the array in matrix fashion, we have the row index * the number of columns + the column index. Instances where such array constructs are required are all denoted by the _matrix suffix to either a class variable name or a function parameter name.
Using this construct means that when matices are passed to functions, a few function parameters have to be reserved for the specification of the dimensions of a particular matrix. I am sure it will become a lot more intuitive once we get to the application of the class towards the end of the article. Users are free to fork the library if not interested in cross platform portability. Back to the description of the class.
//+------------------------------------------------------------------+ //|Constructor | //+------------------------------------------------------------------+ CCoordinateDescent::CCoordinateDescent( const int num_predictors, // Number of predictor variables const int num_observations, // Number of cases we will be training const bool use_covariance_updates, // Use fast covariance updates rather than slow naive method const int num_lambdas_to_trial // Number of m_lambdas we will be using in training )
The parametric constructor requires 4 parameters:
- num_predictors sets the number of variables, this is the number of predictors or indicators, each set of indicators will occupy a column in the internal data matrix.
- num_observations specifies the amount of data the object should expect, this would be the number of rows or the exact number elements available in each set of variables/predictors/indicators.
- use_covariance_updates is a boolean option that should ideally be used when there are more more num_observations than num_predictors.Setting it to true provides significant improvements in excecution time relative to the alternative. This option should be considered only when num_observations > num_predictors.
- num_lambdas_to_trial sets the maximum number of lambda variations that will be tested during the training process.
The constructor simply prepares the internal data structures to receive all the required data.
{
m_nvars = num_predictors ;
m_observs = num_observations ;
m_covarupdates = use_covariance_updates ;
m_nlambda = num_lambdas_to_trial ;
m_initialized=true;
m_ymean=m_yscale=m_explained=0;
if(m_nvars<0 || m_observs<0 || m_nlambda<0)
{
m_initialized=false;
Print("Invalid parameter value, neither num_predictors ,num_observations, nor num_lambdas_to_trial can be negative");
return;
}
if(ArrayResize(m_x_matrix,m_observs*m_nvars)<m_observs*m_nvars ||
ArrayResize(m_y,m_observs)<m_observs ||
ArrayResize(m_xmeans,m_nvars)<m_nvars ||
ArrayResize(m_xscales,m_nvars)<m_nvars ||
ArrayResize(m_beta,m_nvars)<m_nvars ||
ArrayResize(m_resid,m_observs)<m_observs)
m_initialized=false;
//---conditional allocation
if(m_covarupdates)
{
if(ArrayResize(m_xinner_matrix,m_nvars*m_nvars)<m_nvars*m_nvars||
ArrayResize(m_yinner,m_nvars)<m_nvars)
m_initialized=false;
}
//---
if(m_nlambda>0)
{
if(ArrayResize(m_lambdabeta_matrix,m_nlambda*m_nvars)<m_nlambda*m_nvars ||
ArrayResize(m_lambdas,m_nlambda)<m_nlambda)
m_initialized=false;
}
//---return immediately if any error
if(!m_initialized)
Print("Memory allocation error ", GetLastError());
}
Once an instance of CCoordinateDescent is created, we then have to collect all the predictors and target values for preprocessing. This is done by the SetData method. Its first parameter is a starting index showing where in the arrays, to be supplied to this method, to begin collecting data. Doing it this way helps when conducting cross validation later on.
//+------------------------------------------------------------------+ //|Get and standardize the data | //| Also compute inner products if covar_update | //+------------------------------------------------------------------+ bool CCoordinateDescent::SetData( const int begin, // Starting index in full database for getting m_observs of training set const int num_observations,// Number of cases in full database (we wrap back to the start if needed) double &xx_matrix[], // Full database (num_observations rows, m_nvars columns) double &yy[] // Predicted variable vector, num_observations long )
num_observations is parameter name already encountered in the constructor, here it is used a little differently. If a lesser value is set here than the one used at object instantiation, then it enables the ability to revert back to the first value in the array once this index position is reached. If such functionality is not required then set this to the same value used in the constructor call. Just donot set it to zero or below. As this will induce an error.
The next required parameter xx_matrix is an array with the special matrix arrangement discussed. This where we input the raw indicators. It should be of the size specified in the constructor call, ie num_observations * num_predictors.
The last parameter yy is an array of corresponding target values.
The method standardizes both input arrays before copying these to the internal object buffers.
{
if(!m_initialized)
return false;
// parameter checks
if(begin<0 || num_observations<0)
{
Print("Invalid parameter value: neither begin nor num_observations can be negative");
return false;
}
//--- invalid a
if(ArraySize(xx_matrix)<(m_observs*m_nvars) || ArraySize(yy)<m_observs)
{
Print("Insufficient data supplied relative to object specification");
return false;
}
//---
int icase, ivar, jvar, k,xptr;
double sum, xm, xs, diff;
/*
Standardize X
*/
for(ivar=0 ; ivar<m_nvars ; ivar++)
{
xm = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
xm += xx_matrix[k*m_nvars+ivar] ;
}
xm /= m_observs ;
m_xmeans[ivar] = xm ;
xs = 1.e-60 ; // Prevent division by zero later
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
diff = xx_matrix[k*m_nvars+ivar] - xm ;
xs += diff * diff ;
}
xs = sqrt(xs / m_observs) ;
m_xscales[ivar] = xs ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
m_x_matrix[icase*m_nvars+ivar] = (xx_matrix[k*m_nvars+ivar] - xm) / xs ;
}
}
/*
Standardize Y
*/
m_ymean = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
m_ymean += yy[k] ;
}
m_ymean /= m_observs ;
m_yscale = 1.e-60 ; // Prevent division by zero later
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
diff = yy[k] - m_ymean ;
m_yscale += diff * diff ;
}
m_yscale = sqrt(m_yscale / m_observs) ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
m_y[icase] = (yy[k] - m_ymean) / m_yscale ;
}
/*
If user requests covariance updates, compute required inner products
We store the full m_xinner_matrix matrix for faster addressing later,
even though it is symmetric.
We handle both unweighted and weighted cases here.
*/
if(m_covarupdates)
{
for(ivar=0 ; ivar<m_nvars ; ivar++)
{
xptr = ivar ;
// Do XiY
sum = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
sum += m_x_matrix[xptr+icase*m_nvars] * m_y[icase] ;
m_yinner[ivar] = sum / m_observs ;
// Do XiXj
for(jvar=0 ; jvar<m_nvars ; jvar++)
{
if(jvar == ivar)
m_xinner_matrix[ivar*m_nvars+jvar] = 1.0 ; // Recall that X is standardized
else
if(jvar < ivar) // Matrix is symmetric, so just copy
m_xinner_matrix[ivar*m_nvars+jvar] = m_xinner_matrix[jvar*m_nvars+ivar] ;
else
{
sum = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
sum += m_x_matrix[xptr+icase*m_nvars] * m_x_matrix[icase*m_nvars+jvar] ;
m_xinner_matrix[ivar*m_nvars+jvar] = sum / m_observs ;
}
}
} // For ivar
}
//---
return true;
} If SetData completes successfully by returning true, a user is free to call either Train() or TrainLambda() depending on what they want to do.
//+------------------------------------------------------------------+ //|Core training routine | //+------------------------------------------------------------------+ void CCoordinateDescent::Train( const double alpha, // User-specified alpha, (0,1) (0 problematic for descending lambda) const double lambda, // Can be user-specified, but usually from TrainLambda() const int maxits, // Maximum iterations, for safety only const double convergence_criterion, // Convergence criterion, typically 1.e-5 or so const bool fast_test, // Base convergence on max m_beta change vs m_explained variance? const bool warm_start // Start from existing m_beta, rather than zero? )
The Train() method is where core optimization is done. Its here where the type of regularization (alpha) and the degree of regularization (lambda) are specified. Along with the type ofconvergence test to be conducted (fast_test) and the required accuracy for convergence to be attained (convergence_criterion).
- The maxits parameter is a fail safe that prevents the routine from taking an unresonable amount of time to complete, it should be set to a reasonably large value, like 1000 or more.
- warm_start indicates whether to begin training with beta weights initialized to zero or otherwise.
{
if(!m_initialized)
return;
if(alpha<0 || alpha>1)
{
Print("Invalid parameter value: Legal values for alpha are between 0 and 1 inclusive");
return;
}
if(lambda<0)
{
Print("Invalid parameter value: lambda accepts only positive values");
return;
}
if(maxits<=0)
{
Print("Invalid parameter value: maxist accepts only non zero positive values");
return;
}
int i, iter, icase, ivar, kvar, do_active_only, active_set_changed, converged,xptr ;
double residual_sum, S_threshold, argument, new_beta, correction, update_factor ;
double sum, explained_variance, crit, prior_crit, penalty, max_change, Xss, YmeanSquare ;
/*
Initialize
*/
S_threshold = alpha * lambda ; // Threshold for the soft-thresholding operator S()
do_active_only = 0 ; // Begin with a complete pass
prior_crit = 1.0e60 ; // For convergence test
if(warm_start) // Pick up with current betas?
{
if(! m_covarupdates) // If not using covariance updates, must recompute residuals
{
for(icase=0 ; icase<m_observs ; icase++)
{
xptr = icase * m_nvars ;
sum = 0.0 ;
for(ivar=0 ; ivar<m_nvars ; ivar++)
sum += m_beta[ivar] * m_x_matrix[xptr+ivar] ;
m_resid[icase] = m_y[icase] - sum ;
}
}
}
else // Not warm start, so initial betas are all zero
{
for(i=0 ; i<m_nvars ; i++)
m_beta[i] = 0.0 ;
for(i=0 ; i<m_observs ; i++) // Initial residuals are just the Y variable
m_resid[i] = m_y[i] ;
}
// YmeanSquare will remain fixed throughout training.
// Its only use is for computing m_explained variance for the user's edification.
YmeanSquare = 1.0 ;
/*
Outmost loop iterates until converged or user's maxits limit hit
*/
for(iter=0 ; iter<maxits ; iter++)
{
/*
Pass through variables
*/
active_set_changed = 0 ; // Did any betas go to/from 0.0?
max_change = 0.0 ; // For fast convergence test
for(ivar=0 ; ivar<m_nvars ; ivar++) // Descend on this m_beta
{
if(do_active_only && m_beta[ivar] == 0.0)
continue ;
Xss = 1 ; // X was standardized
update_factor = Xss + lambda * (1.0 - alpha) ;
if(m_covarupdates) // Any sensible user will specify this unless m_observs < m_nvars
{
sum = 0.0 ;
for(kvar=0 ; kvar<m_nvars ; kvar++)
sum += m_xinner_matrix[ivar*m_nvars+kvar] * m_beta[kvar] ;
residual_sum = m_yinner[ivar] - sum ;
argument = residual_sum + Xss * m_beta[ivar] ; // Argument to S() [MY FORMULA]
}
else
// Use slow definitional formula (okay if m_observs < m_nvars)
{
residual_sum = 0.0 ;
xptr = ivar ; // Point to column of this variable
for(icase=0 ; icase<m_observs ; icase++)
residual_sum += m_x_matrix[xptr+icase*m_nvars] * m_resid[icase] ; // X_ij * RESID_i
residual_sum /= m_observs ;
argument = residual_sum + m_beta[ivar] ; // Argument to S() ; (Eq 8)
}
// Apply the soft-thresholding operator S()
if(argument > 0.0 && S_threshold < argument)
new_beta = (argument - S_threshold) / update_factor ;
else
if(argument < 0.0 && S_threshold < -argument)
new_beta = (argument + S_threshold) / update_factor ;
else
new_beta = 0.0 ;
// Apply the update, if changed, and adjust the residual if using naive or weighted updates
// This is also used to update the fast convergence criterion
correction = new_beta - m_beta[ivar] ; // Will use this to adjust residual if using naive updates
if(fabs(correction) > max_change)
max_change = fabs(correction) ; // Used for fast convergence criterion
if(correction != 0.0) // Did this m_beta change?
{
if(! m_covarupdates) // Must we update the residual vector (needed for naive methods)?
{
xptr = ivar ; // Point to column of this variable
for(icase=0 ; icase<m_observs ; icase++) // Update residual for this new m_beta
m_resid[icase] -= correction * m_x_matrix[xptr+icase*m_nvars] ;
}
if((m_beta[ivar] == 0.0 && new_beta != 0.0) || (m_beta[ivar] != 0.0 && new_beta == 0.0))
active_set_changed = 1 ;
m_beta[ivar] = new_beta ;
}
} // For all variables; a complete pass
/*
A pass (complete or active only) through variables has been done.
If we are using the fast convergence test, it is simple. But if using the slow method...
Compute m_explained variance and criterion; compare to prior for convergence test
If the user requested the covariance update method, we must compute residuals for these.
*/
if(fast_test) // Quick and simple test
{
if(max_change < convergence_criterion)
converged = 1 ;
else
converged = 0 ;
}
else // Slow test (change in m_explained variance) which requires residual
{
if(m_covarupdates) // We have until now avoided computing residuals
{
for(icase=0 ; icase<m_observs ; icase++)
{
xptr = icase * m_nvars ;
sum = 0.0 ;
for(ivar=0 ; ivar<m_nvars ; ivar++)
sum += m_beta[ivar] * m_x_matrix[xptr+ivar] ; // Cumulate predicted value
m_resid[icase] = m_y[icase] - sum ; // Residual = true - predicted
}
}
sum = 0.0 ; // Will cumulate squared error for convergence test
for(i=0 ; i<m_observs ; i++)
sum += m_resid[i] * m_resid[i] ;
crit = sum / m_observs ; // MSE component of optimization criterion
explained_variance = (YmeanSquare - crit) / YmeanSquare ; // Fraction of Y m_explained
penalty = 0.0 ;
for(i=0 ; i<m_nvars ; i++)
penalty += 0.5 * (1.0 - alpha) * m_beta[i] * m_beta[i] + alpha * fabs(m_beta[i]) ;
penalty *= 2.0 * lambda ; // Regularization component of optimization criterion
crit += penalty ; // This is what we are minimizing
if(prior_crit - crit < convergence_criterion)
converged = 1 ;
else
converged = 0 ;
prior_crit = crit ;
}
/*
After doing a complete (all variables) pass, we iterate on only
the active set (m_beta != 0) until convergence. Then we do a complete pass.
If the active set does not change, we are done:
If a m_beta goes from zero to nonzero, by definition the active set changed.
If a m_beta goes from nonzero to another nonzero, then this is a theoretical flaw
in this process. However, if we just iterated the active set to convergence,
it is highly unlikely that we would get anything other than a tiny move.
*/
if(do_active_only) // Are we iterating on the active set only?
{
if(converged) // If we converged
do_active_only = 0 ; // We now do a complete pass
}
else // We just did a complete pass (all variables)
{
if(converged && ! active_set_changed)
break ;
do_active_only = 1 ; // We now do an active-only pass
}
} // Outer loop iterations
/*
We are done. Compute and save the m_explained variance.
If we did the fast convergence test and covariance updates,
we must compute the residual in order to get the m_explained variance.
Those two options do not require regular residual computation,
so we don't currently have the residual.
*/
if(fast_test && m_covarupdates) // Residuals have not been maintained?
{
for(icase=0 ; icase<m_observs ; icase++)
{
xptr = icase * m_nvars ;
sum = 0.0 ;
for(ivar=0 ; ivar<m_nvars ; ivar++)
sum += m_beta[ivar] * m_x_matrix[xptr+ivar] ;
m_resid[icase] = m_y[icase] - sum ;
}
}
sum = 0.0 ;
for(i=0 ; i<m_observs ; i++)
sum += m_resid[i] * m_resid[i] ;
crit = sum / m_observs ; // MSE component of optimization criterion
m_explained = (YmeanSquare - crit) / YmeanSquare ; // This variable is a member of the class
} As we iterate through observations we also calculate the fraction of explained target variance. When the slow convergence test is used (fast_test set to false), convergence is attained when the change from one iteration to the next is less than the specified convergence criterion value.
Other wise if the fast method is used convergence is achieved when the maximum change in beta adjustment amongst all betas is less than the convergence criterion.
//+------------------------------------------------------------------+ //|Compute minimum lambda such that all betas remain at zero | //+------------------------------------------------------------------+ double CCoordinateDescent::GetLambdaThreshold(const double alpha) { if(!m_initialized) return 0; if(alpha>1 || alpha<0) { Print("Invalid parameter for Alpha, legal values are between 0 and 1 inclusive"); return 0; } int ivar, icase,xptr ; double thresh, sum; thresh = 0.0 ; for(ivar=0 ; ivar<m_nvars ; ivar++) { xptr = ivar ; sum = 0.0 ; for(icase=0 ; icase<m_observs ; icase++) sum += m_x_matrix[xptr+icase*m_nvars] * m_y[icase] ; sum /= m_observs ; sum = fabs(sum) ; if(sum > thresh) thresh = sum ; } return thresh / (alpha + 1.e-60) ; }
GetLambdaThreshold() requires a single input parameter specifying the type of regularization. This method returns the calculated value of lambda for which all corresponding betas are zero. The idea is that, such a value would be a good place to begin searching for the optimal lambda hyperparameter for a given alpha.
The actual optimization of lambda is done by TrainLambda(). It has similar function parameters to Train(). A user can specify the starting lambda value through maxlambda. Setting it to 0 or less automatically engages GetlambdaThreshold() to set the true starting value. The main loop repeatedly calls Train() and saves the betas for each lambda, for a maximum of m_nlambda iterations specified in the constructor call.
//+----------------------------------------------------------------------------------------+ //| Multiple-lambda training routine calls Train() repeatedly, saving each m_beta vector | | //+----------------------------------------------------------------------------------------+ void CCoordinateDescent::TrainLambda( const double alpha, // User-specified alpha, (0,1) (0 problematic for descending lambda) const int maxits, // Maximum iterations, for safety only const double convergence_criterion, // Convergence criterion, typically 1.e-5 or so const bool fast_test, // Base convergence on max m_beta change vs m_explained variance? const double maxlambda, // Starting lambda, or negative for automatic computation const bool print_steps // Print lambda/m_explained table? ) { if(!m_initialized) return; int ivar, ilambda, n_active ; double lambda, min_lambda, lambda_factor,max_lambda=maxlambda; string fprint ; if(m_nlambda <= 1) return ; /* Compute the minimum lambda for which all m_beta weights remain at zero This (slightly decreased) will be the lambda from which we start our descent. */ if(max_lambda <= 0.0) max_lambda = 0.999 * GetLambdaThreshold(alpha) ; min_lambda = 0.001 * max_lambda ; lambda_factor = exp(log(min_lambda / max_lambda) / (m_nlambda-1)) ; /* Repeatedly train with decreasing m_lambdas */ if(print_steps) { fprint+="\nDescending lambda path..."; } lambda = max_lambda ; for(ilambda=0 ; ilambda<m_nlambda ; ilambda++) { m_lambdas[ilambda] = lambda ; // Save in case we want to use later Train(alpha, lambda, maxits, convergence_criterion, fast_test,(bool)ilambda) ; for(ivar=0 ; ivar<m_nvars ; ivar++) m_lambdabeta_matrix[ilambda*m_nvars+ivar] = m_beta[ivar] ; if(print_steps) { n_active = 0 ; for(ivar=0 ; ivar<m_nvars ; ivar++) { if(fabs(m_beta[ivar]) > 0.0) ++n_active ; } fprint+=StringFormat("\n %8.4lf %4d %12.4lf", lambda, n_active, m_explained) ; } lambda *= lambda_factor ; } if(print_steps) Print(fprint); }
Our coordinate descent class is complete. What we require next is a tool to conduct cross validation with, in order to tune the lambda hyperparameter.
OptimizeLambda function
//+------------------------------------------------------------------------------------------+ //| Cross-validation training routine calls TrainLambda() repeatedly to optimize lambda | //+------------------------------------------------------------------------------------------+ double OptimizeLambda( int n_observations, // Number of cases in full database int n_predictors, // Number of variables (columns in database) int n_folds, // Number of folds bool covar_updates, // Does user want (usually faster) covariance update method? int n_lambda, // This many out_lambdas tested by lambda_train() (must be at least 2) double alpha, // User-specified alpha, (0,1) (0 problematic for descending lambda) int maxits, // Maximum iterations, for safety only double convergence_criterion, // Convergence criterion, typically 1.e-5 or so bool fast_test, // Base convergence on max beta change vs explained variance? double &in_matrix[], // Full database (n_observations rows, n_predictors columns) double &in_targets[], // Predicted variable vector, n_observations long double &out_lambdas[], // Returns out_lambdas tested by lambda_train() double &out_lambda_OOS[], // Returns OOS explained for each of above out_lambdas bool print_output = false // show full output )
Its main purpose is to implement cross validation training to automatically select the lambda hyperparameter. Most of its input parameters have familiar names, because the routine uses coordinate descent optimization.
This function can be optionaly used when a user is not sure what value of lambda to use. Cross validation is the go to technique for tuning hyperparameters. To use it we would obviously pass the same training data, that will eventually be used to build the complete regression model.
in_matrix is the input for the matrix of predictors, in_targets is for the corresponding targets. In addition to these input arrays we also have to supply two more arrays. out_lambdas and out_lambda_OOS are arrays that will hold the finer details of the cross validation process.
The last parameter indicates whether to print the results of the process to the terminal.
{
int i_IS, n_IS, i_OOS, n_OOS, n_done, ifold ;
int icase, ivar, ilambda, ibest, k,coefs ;
double pred, sum, diff, max_lambda, Ynormalized, YsumSquares, best,work[] ;
CCoordinateDescent *cd ;
if(n_lambda < 2)
return 0.0 ;
/*
Use the entire dataset to find the max lambda that will be used for all descents.
Also, copy the normalized case weights if there are any.
*/
cd = new CCoordinateDescent(n_predictors, n_observations, covar_updates, n_lambda) ;
cd.SetData(0, n_observations, in_matrix, in_targets) ; // Fetch the training set for this fold
max_lambda = cd.GetLambdaThreshold(alpha) ;
delete cd ;
if(print_output)
PrintFormat("%s starting for %d folds with max lambda=%.9lf",__FUNCTION__, n_folds, max_lambda) ;
i_IS = 0 ; // Training data starts at this index in complete database
n_done = 0 ; // Number of cases treated as OOS so far
for(ilambda=0 ; ilambda<n_lambda ; ilambda++)
out_lambda_OOS[ilambda] = 0.0 ; // Will cumulate across folds here
YsumSquares = 0.0 ; // Will cumulate to compute explained fraction
/*
Process the folds
*/
for(ifold=0 ; ifold<n_folds ; ifold++)
{
n_OOS = (n_observations - n_done) / (n_folds - ifold) ; // Number OOS (test set)
n_IS = n_observations - n_OOS ; // Number IS (training set)
i_OOS = (i_IS + n_IS) % n_observations ; // OOS starts at this index
// Train the model with this IS set
cd = new CCoordinateDescent(n_predictors, n_IS, covar_updates, n_lambda) ;
cd.SetData(i_IS, n_observations, in_matrix, in_targets) ; // Fetch the training set for this fold
cd.TrainLambda(alpha, maxits, convergence_criterion, fast_test, max_lambda,print_output) ; // Compute the complete set of betas (all out_lambdas)
// Compute OOS performance for each lambda and sum across folds.
// Normalization of X and Y is repeated, when it could be done once and saved.
// But the relative cost is minimal, and it is simpler doing it this way.
for(ilambda=0 ; ilambda<n_lambda ; ilambda++)
{
out_lambdas[ilambda] = cd.GetLambdaAt(ilambda) ; // This will be the same for all folds
coefs = ilambda * n_predictors ;
sum = 0.0 ;
for(icase=0 ; icase<n_OOS ; icase++)
{
k = (icase + i_OOS) % n_observations ;
pred = 0.0 ;
for(ivar=0 ; ivar<n_predictors ; ivar++)
pred += cd.GetLambdaBetaAt(coefs+ivar) * (in_matrix[k*n_predictors+ivar] - cd.GetXmeansAt(ivar)) / cd.GetXscalesAt(ivar) ;
Ynormalized = (in_targets[k] - cd.GetYmean()) / cd.GetYscale() ;
diff = Ynormalized - pred ;
if(ilambda == 0)
YsumSquares += Ynormalized * Ynormalized ;
sum += diff * diff ;
}
out_lambda_OOS[ilambda] += sum ; // Cumulate for this fold
} // For ilambda
delete cd ;
n_done += n_OOS ; // Cumulate OOS cases just processed
i_IS = (i_IS + n_OOS) % n_observations ; // Next IS starts at this index
} // For ifold
/*
Compute OOS explained variance for each lambda, and keep track of the best
*/
best = -1.e60 ;
for(ilambda=0 ; ilambda<n_lambda ; ilambda++)
{
out_lambda_OOS[ilambda] = (YsumSquares - out_lambda_OOS[ilambda]) / YsumSquares ;
if(out_lambda_OOS[ilambda] > best)
{
best = out_lambda_OOS[ilambda] ;
ibest = ilambda ;
}
}
if(print_output)
PrintFormat("\n%s ending with best lambda=%9.9lf explained=%9.9lf",__FUNCTION__, out_lambdas[ibest], best) ;
return out_lambdas[ibest] ;
}
//+------------------------------------------------------------------+
The function uses a local instance of CCoordinateDescent to test a set of lambdas. The number of tested lambdas is set by the n_lambda parameter of the function. Tested lambdas begin from the maximum calculated by calling GetLambdaThreshold(). After each testing iteration the previous lambda value is decreased slightly.Each lambda test generates new beta coefficients that are used to calculate the fraction of explained variance. All this is done for each fold. The results from all folds are examined and the best is selected. The lambda that gave the best result is returned as the optimal lambda.
With all the code utilities described, its time to put them to work.
An Example
To demonstrate the practical application of this method, we will use it to build a model that predicts the price change to the next bar based on a bunch of long and short moving averages. We want to find the set of moving averages that are most useful for predicting the next bar's price change.
To implement this we supply the model with indicators calculated based on log transformed raw prices, with the targets being the log differences. We need an indicator that log tranforms raw prices, so that other indicators (in this case being the moving average) can reference it. The log prices indicator is shown below.
//+------------------------------------------------------------------+ //| LogPrices.mq5 | //| Copyright 2023, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 //--- plot Log #property indicator_label1 "Log" #property indicator_type1 DRAW_LINE #property indicator_color1 clrTurquoise #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- indicator buffers double LogBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,LogBuffer,INDICATOR_DATA); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- for(int i=(prev_calculated>0)?prev_calculated-1:0; i<rates_total; i++) LogBuffer[i]=(price[i]>0)?log(price[i]):0; //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
The training program will be implemented as a script. We begin by specifying the essential include files and the script's inputs. The inputs allow a user to adjust various aspects of the program to suit their needs. This includes the ability to set the dates for the training and testing time spans.
//+------------------------------------------------------------------+ //| ElasticNetRegressionModel_MA.mq5 | //| Copyright 2023, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\LogPrices.ex5" #include<CoordinateDescent.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //--- input parameters input uint MA_period_inc=2; //MA lookback increment input uint Num_MA_periods=30; //Num of lookbacks input double Alpha=0.5; input int AppliedPrice=PRICE_CLOSE; input ENUM_MA_METHOD MaMethod=MODE_EMA; input ENUM_TIMEFRAMES tf=PERIOD_D1; //time frame input uint BarsLookAhead=1; input uint Num_Folds = 10; //Num of Folds for cross validation input uint MaximumIterations=1000; input datetime TrainingSampleStartDate=D'2019.12.31'; input datetime TrainingSampleStopDate=D'2022.12.31'; input datetime TestingSampleStartDate=D'2023.01.02'; input datetime TestingSampleStopDate=D'2023.06.30'; input string SetSymbol=""; input bool UseCovarUpdates=true; input bool UseFastTest=true; input bool UseWarmStart=false; input int NumLambdasToTest=50; input bool ShowFullOutPut=false; //print full output to terminal
Important user input options are the MA_period_inc input which sets the period increments. Num_Ma_periods defines the number of moving averages that will be supplied to the algorithm. The indicator values to be used as predictors will be the difference between a long and short moving average. The short moving average is calculated as being half of the period of the resulting long moving average. The long moving average is determined by incrementing by MA_period_inc , Num_MA_period times.
Num_Folds stipulates the number of folds to be used by the Optimizelambda function during cross validation.
Other inputs are self explanatory.
The script begins by enumerating the training and testing data sets. Local buffers are resized based on the chosen user inputs.
//+------------------------------------------------------------------+ //|global integer variables | //+------------------------------------------------------------------+ int size_insample, //training set size size_outsample, //testing set size size_observations, //size of of both training and testing sets combined size_lambdas, //number of lambdas to be tested size_predictors, //number of predictors maxperiod, //maximum lookback price_handle=INVALID_HANDLE, //log prices indicator handle long_ma_handle=INVALID_HANDLE, //long moving average indicator handle short_ma_handle=INVALID_HANDLE;//short moving average indicator handle //+------------------------------------------------------------------+ //|double global variables | //+------------------------------------------------------------------+ double prices[], //array for log transformed prices targets[], //differenced prices kept here predictors_matrix[], //flat array arranged as matrix of all predictors_matrix ie size_observations by size_predictors longma[], //long ma indicator values Lambdas[], //calculated lambdas kept here Lambdas_OOS[], //calculated out of sample lambdas are here shortma[], //short ma indicator values Lambda; //initial optimal lambda value //+------------------------------------------------------------------+ //| Coordinate descent pointer | //+------------------------------------------------------------------+ CCoordinateDescent *cdmodel; //coordinate descent pointer //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //get relative shift of is and oos sets int teststart,teststop,trainstart,trainstop; teststart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestingSampleStartDate); teststop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestingSampleStopDate); trainstart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStartDate); trainstop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStopDate); //check for errors from ibarshift calls if(teststart<0 || teststop<0 || trainstart<0 || trainstop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(trainstart - teststop) + 1 ; size_outsample=(teststart - teststop) + 1; size_insample=(trainstart - trainstop) + 1; maxperiod=int(Num_MA_periods*MA_period_inc); size_insample-=maxperiod; size_lambdas=NumLambdasToTest; size_predictors=int(Num_MA_periods); //---check for input errors if(size_lambdas<=0 || size_insample<=0 || size_outsample<=0 || size_predictors<=0 || maxperiod<=0 || BarsLookAhead<=0) { Print("Invalid inputs "); return; } //--- Comment("resizing buffers...");
Arrays that will passed to the CCoordinateDescent instance are prepared and filled, this being the targets array and the matrix of predictors.
//---allocate memory if(ArrayResize(targets,size_observations)<(int)size_observations || ArrayResize(predictors_matrix,size_observations*size_predictors)<int(size_observations*size_predictors) || ArrayResize(Lambdas,size_lambdas)<(int)size_lambdas || ArrayResize(Lambdas_OOS,size_lambdas)<(int)size_lambdas || ArrayResize(shortma,size_observations)<(int)size_observations || ArrayResize(longma,size_observations)<(int)size_observations || ArrayResize(prices,size_observations+BarsLookAhead)<int(size_observations+BarsLookAhead)) { Print("ArrayResize error ",ErrorDescription(GetLastError())); return; } //--- Comment("getting price predictors_matrix..."); //---set prices handle price_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,tf,"::Indicators\\LogPrices.ex5",AppliedPrice); if(price_handle==INVALID_HANDLE) { Print("invalid logprices handle ",ErrorDescription(GetLastError())); return; } //--- Comment("getting indicators..."); //----calculate the full collection of predictors_matrix int longmaperiod,shortmaperiod,prevshort,prevlong; int k=0; //--- prevlong=prevshort=0; //--- for(uint iperiod=0; iperiod<Num_MA_periods; iperiod++) { longmaperiod=(int)(iperiod+1)*int(MA_period_inc); shortmaperiod = (longmaperiod>=2)?int(longmaperiod/2):longmaperiod; ResetLastError(); int try=10; while(try) { long_ma_handle=iMA(SetSymbol!=""?SetSymbol:NULL,tf,longmaperiod,0,MaMethod,price_handle); short_ma_handle=iMA(SetSymbol!=""?SetSymbol:NULL,tf,shortmaperiod,0,MaMethod,price_handle); if(long_ma_handle==INVALID_HANDLE || short_ma_handle==INVALID_HANDLE) try--; else break; } Comment("copying buffers for short ",shortmaperiod," long ",longmaperiod); if(CopyBuffer(long_ma_handle,0,teststop,size_observations,longma)<=0 || CopyBuffer(short_ma_handle,0,teststop,size_observations,shortma)<=0) { Print("error copying to ma buffers ",GetLastError()); return; } for(int i=0 ; i<int(size_observations) ; i++) predictors_matrix[i*size_predictors+k] = shortma[i]-longma[i]; ++k ; if(long_ma_handle!=INVALID_HANDLE && short_ma_handle!=INVALID_HANDLE && IndicatorRelease(long_ma_handle) && IndicatorRelease(short_ma_handle)) { long_ma_handle=short_ma_handle=INVALID_HANDLE; prevlong=longmaperiod; prevshort=shortmaperiod; } } //--- Comment("filling target buffer..."); //--- ResetLastError(); if(CopyBuffer(price_handle,0,teststop,size_observations+BarsLookAhead,prices)<int(size_observations+BarsLookAhead)) { Print("error copying to price buffer , ",ErrorDescription(GetLastError())); return; } //--- for(int i=0 ; i<int(size_observations); i++) targets[i] = prices[i+BarsLookAhead]-prices[i]; //---
Lambda tuning is done depending on the value of Alpha. When alpha is less than or equal to zero, no optimal lambda is calculated. The result will be a model that resembles standard linear regression without any regularization.
//--- Comment("optional lambda tuning..."); //--- if(Alpha<=0) Lambda=0; else //train Lambda=OptimizeLambda(size_insample,size_predictors,(int)Num_Folds,UseCovarUpdates,size_lambdas,Alpha,(int)MaximumIterations,1.e-9,UseFastTest,predictors_matrix,targets,Lambdas,Lambdas_OOS,ShowFullOutPut); //---
Once training is completed by the CCoordinateDescent object the results can be optionally output to the terminal.
Comment("coordinate descent engagement..."); //---initialize CD object cdmodel=new CCoordinateDescent(size_predictors,size_insample,UseCovarUpdates,0); //--- if(cdmodel==NULL) { Print("error creating Coordinate Descent object "); return; } //---set the parameters and data cdmodel.SetData(0,size_insample,predictors_matrix,targets); //--- Print("optimal lambda ",DoubleToString(Lambda)); //---train the model cdmodel.Train(Alpha,Lambda,(int)MaximumIterations,1.e-7,UseFastTest,UseWarmStart); //--- Print("explained variance ",cdmodel.GetExplainedVariance()); //---optionally output results of training here if(ShowFullOutPut) { k=0; string output; for(uint iperiod=0; iperiod<Num_MA_periods; iperiod++) { longmaperiod=(int)(iperiod+1)*int(MA_period_inc); output+=StringFormat("\n%5d ", longmaperiod) ; shortmaperiod = (longmaperiod>=2)?int(longmaperiod/2):longmaperiod; output+=StringFormat(",%5d ,%9.9lf ", shortmaperiod,cdmodel.GetBetaAt(k)); ++k; } Print(output); } //---
Program output will be displayed in columns, the first column shows the long moving average period, the second displays the corresponding short moving average and finally the beta value for that particular predictor is given. If zero is displayed, it means that this predictor was discarded.
double sum=0.0; //cumulated predictions double pred; //a prediction int xptr; k=size_observations - (size_insample+maxperiod) - 1; //--- Comment("test the model..."); //---do the out of sample test for(int i=k ; i<size_observations ; i++) { xptr = i*size_predictors ; pred = 0.0 ; for(int ivar=0 ; ivar<int(size_predictors) ; ivar++) pred += cdmodel.GetBetaAt(ivar) * (predictors_matrix[xptr+ivar] - cdmodel.GetXmeansAt(ivar)) / cdmodel.GetXscalesAt(ivar) ; pred = pred * cdmodel.GetYscale() + cdmodel.GetYmean() ; // Unscale prediction to get it back in original Y domain if(pred > 0.0) sum += targets[i] ; else if(pred < 0.0) sum -= targets[i] ; } //--- PrintFormat("OOS total return = %.5lf (%.3lf percent)",sum, 100.0 * (exp(sum) - 1.0)) ; //--- delete cdmodel; //--- Comment("");
The program ends after examining performance over the selected testing period. Users should note that the perfomance value displayed at program end is not an indication of true performance as there is a lot not taken into consideration. These figures should be used relative to other results obtained from different program parameter sets.
The output below shows the results when Alpha is 0. As stated earlier, when alpha is 0, there is no regularization, the model is built using all the supplied predictors, none are left out.
DH 0 19:58:47.521 ELN_MA (GBPUSD,D1) optimal lambda 0.00000000 HP 0 19:58:47.552 ELN_MA (GBPUSD,D1) explained variance 0.9914167039554915 ID 0 19:58:47.552 ELN_MA (GBPUSD,D1) FF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 2 , 1 ,1.85143599128379721108e+00 JJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 4 , 2 ,-2.44139247803866465958e+00 MR 0 19:58:47.552 ELN_MA (GBPUSD,D1) 6 , 3 ,2.32230838054034549600e+00 HF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 8 , 4 ,-2.35763762038486313077e-01 FJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 10 , 5 ,-5.12822602346063693979e-01 MP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 12 , 6 ,-2.63526268082343251287e-01 CF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 14 , 7 ,-4.66454472659737495732e-02 FN 0 19:58:47.552 ELN_MA (GBPUSD,D1) 16 , 8 ,6.22551516067148258404e-02 KP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 18 , 9 ,9.45364603399752728707e-02 JK 0 19:58:47.552 ELN_MA (GBPUSD,D1) 20 , 10 ,8.71627177974267641769e-02 JM 0 19:58:47.552 ELN_MA (GBPUSD,D1) 22 , 11 ,6.43970377784374714558e-02 CG 0 19:58:47.552 ELN_MA (GBPUSD,D1) 24 , 12 ,3.92137206481772693234e-02 FI 0 19:58:47.552 ELN_MA (GBPUSD,D1) 26 , 13 ,1.74528224486318189745e-02 HS 0 19:58:47.552 ELN_MA (GBPUSD,D1) 28 , 14 ,1.04642691815316421500e-03 PG 0 19:58:47.552 ELN_MA (GBPUSD,D1) 30 , 15 ,-9.98741520244338966406e-03 RM 0 19:58:47.552 ELN_MA (GBPUSD,D1) 32 , 16 ,-1.64348263919291276425e-02 CS 0 19:58:47.552 ELN_MA (GBPUSD,D1) 34 , 17 ,-1.93143258653755492404e-02 QI 0 19:58:47.552 ELN_MA (GBPUSD,D1) 36 , 18 ,-1.96075858211104264717e-02 FO 0 19:58:47.552 ELN_MA (GBPUSD,D1) 38 , 19 ,-1.81510403514190954422e-02 RD 0 19:58:47.552 ELN_MA (GBPUSD,D1) 40 , 20 ,-1.56082180218151990447e-02 PJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 42 , 21 ,-1.24793265043600110076e-02 HP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 44 , 22 ,-9.12541199880392318866e-03 MF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 46 , 23 ,-5.79584482050124645547e-03 DL 0 19:58:47.552 ELN_MA (GBPUSD,D1) 48 , 24 ,-2.65399377323665905393e-03 PP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 50 , 25 ,2.00883928121427593472e-04 RJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 52 , 26 ,2.71594753051577000869e-03 IL 0 19:58:47.552 ELN_MA (GBPUSD,D1) 54 , 27 ,4.87097208116808733092e-03 IF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 56 , 28 ,6.66787159270224374930e-03 MH 0 19:58:47.552 ELN_MA (GBPUSD,D1) 58 , 29 ,8.12292277995673578372e-03 NR 0 19:58:47.552 ELN_MA (GBPUSD,D1) 60 , 30 ,9.26111235731779183777e-03 JG 0 19:58:47.568 ELN_MA (GBPUSD,D1) OOS total return = 3.42660 (2977.187 percent)
Below is output when Alpha is 0.1. Of interest are beta values in comparison to the previous run. Zero beta values show that the corresponding predictor was discarded.
NP 0 19:53:32.412 ELN_MA (GBPUSD,D1) optimal lambda 0.00943815 HH 0 19:53:32.458 ELN_MA (GBPUSD,D1) explained variance 0.9748473636648924 GL 0 19:53:32.458 ELN_MA (GBPUSD,D1) GN 0 19:53:32.458 ELN_MA (GBPUSD,D1) 2 , 1 ,1.41004781317849103850e+00 MR 0 19:53:32.458 ELN_MA (GBPUSD,D1) 4 , 2 ,-6.98106822708694618740e-01 DJ 0 19:53:32.458 ELN_MA (GBPUSD,D1) 6 , 3 ,0.00000000000000000000e+00 NL 0 19:53:32.458 ELN_MA (GBPUSD,D1) 8 , 4 ,1.30221271072762545540e-01 MG 0 19:53:32.458 ELN_MA (GBPUSD,D1) 10 , 5 ,1.13824982442231326107e-01 DI 0 19:53:32.458 ELN_MA (GBPUSD,D1) 12 , 6 ,0.00000000000000000000e+00 IS 0 19:53:32.458 ELN_MA (GBPUSD,D1) 14 , 7 ,0.00000000000000000000e+00 NE 0 19:53:32.458 ELN_MA (GBPUSD,D1) 16 , 8 ,0.00000000000000000000e+00 GO 0 19:53:32.458 ELN_MA (GBPUSD,D1) 18 , 9 ,0.00000000000000000000e+00 JP 0 19:53:32.458 ELN_MA (GBPUSD,D1) 20 , 10 ,0.00000000000000000000e+00 DH 0 19:53:32.458 ELN_MA (GBPUSD,D1) 22 , 11 ,-3.69006880128594713653e-02 OM 0 19:53:32.458 ELN_MA (GBPUSD,D1) 24 , 12 ,-2.43715386443472993572e-02 LS 0 19:53:32.458 ELN_MA (GBPUSD,D1) 26 , 13 ,-3.50967791710741789518e-03 DK 0 19:53:32.458 ELN_MA (GBPUSD,D1) 28 , 14 ,0.00000000000000000000e+00 LM 0 19:53:32.458 ELN_MA (GBPUSD,D1) 30 , 15 ,0.00000000000000000000e+00 KG 0 19:53:32.458 ELN_MA (GBPUSD,D1) 32 , 16 ,0.00000000000000000000e+00 RI 0 19:53:32.458 ELN_MA (GBPUSD,D1) 34 , 17 ,0.00000000000000000000e+00 ES 0 19:53:32.458 ELN_MA (GBPUSD,D1) 36 , 18 ,0.00000000000000000000e+00 PE 0 19:53:32.458 ELN_MA (GBPUSD,D1) 38 , 19 ,0.00000000000000000000e+00 KO 0 19:53:32.458 ELN_MA (GBPUSD,D1) 40 , 20 ,0.00000000000000000000e+00 NQ 0 19:53:32.458 ELN_MA (GBPUSD,D1) 42 , 21 ,0.00000000000000000000e+00 QK 0 19:53:32.458 ELN_MA (GBPUSD,D1) 44 , 22 ,0.00000000000000000000e+00 PM 0 19:53:32.458 ELN_MA (GBPUSD,D1) 46 , 23 ,0.00000000000000000000e+00 GG 0 19:53:32.458 ELN_MA (GBPUSD,D1) 48 , 24 ,0.00000000000000000000e+00 OI 0 19:53:32.458 ELN_MA (GBPUSD,D1) 50 , 25 ,0.00000000000000000000e+00 PS 0 19:53:32.458 ELN_MA (GBPUSD,D1) 52 , 26 ,0.00000000000000000000e+00 RE 0 19:53:32.458 ELN_MA (GBPUSD,D1) 54 , 27 ,1.14149417738317331301e-03 FO 0 19:53:32.458 ELN_MA (GBPUSD,D1) 56 , 28 ,3.18638349345921325848e-03 IQ 0 19:53:32.458 ELN_MA (GBPUSD,D1) 58 , 29 ,3.87574752936066481077e-03 KK 0 19:53:32.458 ELN_MA (GBPUSD,D1) 60 , 30 ,3.16472282935538083357e-03 QN 0 19:53:32.474 ELN_MA (GBPUSD,D1) OOS total return = 3.40954 (2925.133 percent)
Next we view the output when Alpha is 0.9, this time we highlight the ouput from LambdaOptimize. The first column is the lambda value tested , the second column shows the number of predictors included in the model, and the last column shows the fraction of explained variance from the test, for a particular fold. In the script we specified 10 folds, so there are ten tables of this data.
ME 0 19:57:21.630 ELN_MA (GBPUSD,D1) OptimizeLambda starting for 10 folds with max lambda=1.048683301 JE 0 19:57:21.833 ELN_MA (GBPUSD,D1) RO 0 19:57:21.833 ELN_MA (GBPUSD,D1) Descending lambda path... RE 0 19:57:21.833 ELN_MA (GBPUSD,D1) 1.0487 0 0.0000 NM 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.9108 1 0.2009 ND 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.7910 1 0.3586 RL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.6870 1 0.4813 LD 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.5967 1 0.5764 OL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.5182 1 0.6499 KG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.4501 1 0.7065 LO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.3909 1 0.7500 JG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.3395 1 0.7833 QO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.2949 1 0.8088 OF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.2561 1 0.8282 CN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.2224 1 0.8431 CF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1932 1 0.8544 HN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1678 1 0.8630 LI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1457 1 0.8695 GQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1266 1 0.8744 LI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1099 2 0.8788 QQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0955 2 0.8914 PH 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0829 2 0.9019 IP 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0720 2 0.9098 EH 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0625 2 0.9159 RP 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0543 2 0.9205 EK 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0472 3 0.9325 HS 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0410 2 0.9424 NK 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0356 2 0.9467 HS 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0309 2 0.9500 KJ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0268 2 0.9525 JR 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0233 3 0.9556 GJ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0202 3 0.9586 NR 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0176 4 0.9610 CM 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0153 3 0.9635 CE 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0133 4 0.9656 OM 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0115 3 0.9677 PE 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0100 3 0.9689 QL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0087 5 0.9707 CD 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0075 4 0.9732 RL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0066 5 0.9745 ND 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0057 5 0.9756 NO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0049 4 0.9767 HG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0043 4 0.9776 IO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0037 5 0.9784 EG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0032 6 0.9793 KN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0028 6 0.9808 DF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0024 8 0.9825 HN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0021 6 0.9840 PF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0018 7 0.9847 OQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0016 7 0.9855 OI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0014 5 0.9862 DQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0012 7 0.9867 MI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0010 8 0.9874 KS 0 19:57:22.068 ELN_MA (GBPUSD,D1) OF 0 19:57:22.068 ELN_MA (GBPUSD,D1) Descending lambda path... OL 0 19:57:22.068 ELN_MA (GBPUSD,D1) 1.0487 0 0.0000 RG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.9108 1 0.2006 PO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.7910 1 0.3583 JG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.6870 1 0.4810 RO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.5967 1 0.5761 NF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.5182 1 0.6495 RN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.4501 1 0.7061 OF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.3909 1 0.7496 RN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.3395 1 0.7829 LI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.2949 1 0.8084 NQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.2561 1 0.8279 OI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.2224 1 0.8427 JQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1932 1 0.8540 LH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1678 1 0.8626 QP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1457 1 0.8691 MH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1266 1 0.8741 IP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1099 3 0.8794 NK 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0955 2 0.8929 PS 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0829 2 0.9029 NK 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0720 2 0.9106 RS 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0625 2 0.9164 JJ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0543 3 0.9225 MR 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0472 3 0.9348 KJ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0410 2 0.9433 MR 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0356 2 0.9474 KM 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0309 2 0.9506 JE 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0268 2 0.9529 FM 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0233 3 0.9559 KE 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0202 3 0.9589 DL 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0176 3 0.9616 CD 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0153 3 0.9636 ML 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0133 3 0.9663 CD 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0115 3 0.9678 KO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0100 4 0.9691 EG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0087 5 0.9719 RO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 KG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0066 4 0.9751 IN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0057 5 0.9763 MF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0049 4 0.9774 FN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0043 4 0.9784 EF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0037 5 0.9792 QQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0032 6 0.9802 NI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0028 7 0.9818 HQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0024 7 0.9834 EI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0021 5 0.9847 HP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0018 6 0.9854 KH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0016 7 0.9861 FP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0014 5 0.9866 GH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0012 6 0.9871 PS 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0010 7 0.9877 MH 0 19:57:22.318 ELN_MA (GBPUSD,D1) EL 0 19:57:22.318 ELN_MA (GBPUSD,D1) Descending lambda path... CF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 1.0487 1 0.0003 HN 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.9108 1 0.2020 IF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.7910 1 0.3597 QQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.6870 1 0.4824 GI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.5967 1 0.5775 LQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.5182 1 0.6510 JI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.4501 1 0.7076 OP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.3909 1 0.7511 NH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.3395 1 0.7845 MP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.2949 1 0.8100 IH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.2561 1 0.8294 CS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.2224 1 0.8443 QK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1932 1 0.8556 IS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1678 1 0.8641 QK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1457 1 0.8707 ER 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1266 1 0.8756 QJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1099 2 0.8805 GR 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0955 2 0.8928 LJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0829 2 0.9032 FE 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0720 2 0.9111 HM 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0625 2 0.9171 LE 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0543 2 0.9217 OM 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0472 3 0.9315 GD 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0410 3 0.9421 EL 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 HD 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 DL 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 OG 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 JO 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 OG 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 CO 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0153 3 0.9638 MF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0133 4 0.9659 LN 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 FF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0100 4 0.9694 PN 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0087 5 0.9709 RI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0075 4 0.9738 JQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0066 5 0.9751 KI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0057 5 0.9763 GQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0049 4 0.9774 MH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0043 4 0.9783 QP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0037 4 0.9791 DH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 QP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0028 6 0.9812 LK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 GS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0021 8 0.9842 OK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0018 6 0.9853 IS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0016 7 0.9861 DJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0014 6 0.9869 RR 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0012 6 0.9874 PJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0010 7 0.9879 DQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) PK 0 19:57:22.568 ELN_MA (GBPUSD,D1) Descending lambda path... KQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 1.0487 1 0.0004 FI 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.9108 1 0.2021 IP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.7910 1 0.3598 KH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.6870 1 0.4825 LP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.5967 1 0.5777 RH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.5182 1 0.6511 IS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.4501 1 0.7078 KK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.3909 1 0.7512 JS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.3395 1 0.7846 OK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.2949 1 0.8101 KR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.2561 1 0.8295 CJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.2224 1 0.8444 CR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1932 1 0.8557 FJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1678 1 0.8643 QE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1457 1 0.8708 GM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1266 1 0.8757 OE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1099 2 0.8808 NM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0955 2 0.8931 CD 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0829 2 0.9034 IL 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0720 2 0.9113 KD 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0625 2 0.9173 DL 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0543 2 0.9218 RG 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0472 3 0.9319 IO 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0410 3 0.9424 NG 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0356 2 0.9474 CO 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0309 2 0.9507 OF 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0268 2 0.9532 CN 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0233 3 0.9560 DF 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0202 3 0.9590 PN 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0176 3 0.9613 QI 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0153 3 0.9639 PQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0133 4 0.9659 JI 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0115 3 0.9681 GQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0100 4 0.9694 LH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0087 6 0.9710 LP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0075 5 0.9738 LH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0066 4 0.9751 QP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0057 4 0.9763 MK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0049 5 0.9774 OS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0043 5 0.9783 CK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0037 5 0.9791 JS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0032 5 0.9801 DJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0028 7 0.9813 DR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0024 7 0.9828 HJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0021 7 0.9843 NR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0018 6 0.9853 KM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0016 7 0.9860 NE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 IM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 GE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0010 8 0.9878 JO 0 19:57:22.740 ELN_MA (GBPUSD,D1) RQ 0 19:57:22.740 ELN_MA (GBPUSD,D1) Descending lambda path... PK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 1.0487 1 0.0003 DS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.9108 1 0.2021 GK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.7910 1 0.3598 MS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.6870 1 0.4825 MJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.5967 1 0.5776 PR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.5182 1 0.6511 NJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.4501 1 0.7077 MR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.3909 1 0.7512 IM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.3395 1 0.7845 RE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.2949 1 0.8100 MM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.2561 1 0.8295 HE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.2224 1 0.8443 FL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1932 1 0.8556 CD 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1678 1 0.8642 OL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1457 1 0.8708 ID 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1266 1 0.8757 DO 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1099 2 0.8807 DG 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0955 2 0.8928 GO 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0829 2 0.9032 HG 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0720 2 0.9112 NN 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0625 2 0.9172 FF 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0543 2 0.9218 JN 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0472 3 0.9313 MF 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0410 3 0.9419 RQ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 CI 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 PQ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0268 2 0.9531 LI 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 PP 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0202 4 0.9588 QH 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0176 3 0.9612 PP 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0153 3 0.9638 DH 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0133 4 0.9657 GS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 IK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0100 4 0.9694 DS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0087 5 0.9708 GK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 MR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 PJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 RR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 RJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 FE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 GM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 FE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0028 6 0.9812 OM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 ID 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0021 7 0.9842 KL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0018 6 0.9852 ND 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0016 6 0.9860 LL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 GG 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 IO 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0010 7 0.9877 KD 0 19:57:23.052 ELN_MA (GBPUSD,D1) OH 0 19:57:23.052 ELN_MA (GBPUSD,D1) Descending lambda path... RR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 1.0487 1 0.0002 DJ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.9108 1 0.2019 LR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.7910 1 0.3596 JM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.6870 1 0.4823 ME 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.5967 1 0.5775 RM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.5182 1 0.6509 LE 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.4501 1 0.7076 FL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.3909 1 0.7510 GD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.3395 1 0.7844 HL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.2949 1 0.8099 RD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.2561 1 0.8293 RO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.2224 1 0.8442 FG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1932 1 0.8555 KO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1678 1 0.8641 DG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1457 1 0.8706 RN 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1266 1 0.8755 DF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 HN 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0955 2 0.8927 GF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 OQ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0720 2 0.9110 MI 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0625 2 0.9170 IQ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0543 2 0.9216 DI 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0472 3 0.9316 LP 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0410 3 0.9422 OH 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 NP 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 RH 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 ES 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 LK 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 ES 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 DK 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0153 3 0.9637 HR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 JJ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 MR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 CJ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0087 6 0.9709 RE 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 LM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 IE 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 OM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 GD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 CL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 CD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0032 5 0.9799 DL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 JG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 HO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0021 6 0.9843 CG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0018 5 0.9852 LO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0016 7 0.9860 EF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 JN 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 EF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0010 8 0.9877 KM 0 19:57:23.302 ELN_MA (GBPUSD,D1) CG 0 19:57:23.302 ELN_MA (GBPUSD,D1) Descending lambda path... EM 0 19:57:23.302 ELN_MA (GBPUSD,D1) 1.0487 1 0.0003 ID 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.9108 1 0.2021 NL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.7910 1 0.3598 PD 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.6870 1 0.4825 HL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.5967 1 0.5776 MG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.5182 1 0.6511 GO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.4501 1 0.7077 PG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.3909 1 0.7512 MO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.3395 1 0.7846 KF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.2949 1 0.8100 HN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.2561 1 0.8295 HF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.2224 1 0.8444 PN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1932 1 0.8557 JI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1678 1 0.8642 FQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1457 1 0.8708 DI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1266 1 0.8757 PQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 LH 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0955 2 0.8927 KP 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 DH 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0720 2 0.9111 JP 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0625 2 0.9171 NK 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0543 2 0.9217 PS 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0472 3 0.9316 HK 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0410 3 0.9422 CS 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 JJ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 ER 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0268 2 0.9531 RJ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0233 3 0.9559 GR 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0202 3 0.9589 LM 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0176 3 0.9612 EE 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0153 3 0.9638 LM 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 NE 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 IL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 OD 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0087 6 0.9709 EL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0075 4 0.9737 GD 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0066 4 0.9751 NO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0057 4 0.9763 CG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 KO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 PG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0037 4 0.9790 FN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 PF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 NN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 LF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0021 7 0.9842 RQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0018 6 0.9852 HI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0016 7 0.9860 PQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0014 6 0.9867 NI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 QP 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0010 8 0.9877 EK 0 19:57:23.537 ELN_MA (GBPUSD,D1) QM 0 19:57:23.537 ELN_MA (GBPUSD,D1) Descending lambda path... PG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 1.0487 1 0.0002 NO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.9108 1 0.2019 NG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.7910 1 0.3596 PO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.6870 1 0.4823 KF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.5967 1 0.5775 HN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.5182 1 0.6509 KF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.4501 1 0.7075 LN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.3909 1 0.7510 II 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.3395 1 0.7844 RQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.2949 1 0.8099 PI 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.2561 1 0.8293 HQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.2224 1 0.8442 DH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1932 1 0.8555 FP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1678 1 0.8640 FH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1457 1 0.8706 HP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1266 1 0.8755 FK 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 RS 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0955 2 0.8927 IK 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 IS 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0720 2 0.9110 KJ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0625 2 0.9170 OR 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0543 2 0.9216 FJ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0472 3 0.9316 CR 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0410 3 0.9421 QM 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 DE 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 PM 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 KE 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 NL 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 KD 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 FL 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0153 3 0.9637 RD 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 HO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 CG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 EO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0087 6 0.9709 HG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 NN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 OF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 QN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 QF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 EQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 HI 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 FQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 PI 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 JP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0021 6 0.9843 MH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0018 5 0.9852 MP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0016 6 0.9860 KH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 HS 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 KK 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0010 8 0.9877 PP 0 19:57:23.880 ELN_MA (GBPUSD,D1) HD 0 19:57:23.880 ELN_MA (GBPUSD,D1) Descending lambda path... GN 0 19:57:23.880 ELN_MA (GBPUSD,D1) 1.0487 1 0.0000 DF 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.9108 1 0.2018 FQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.7910 1 0.3595 JI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.6870 1 0.4822 HQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.5967 1 0.5773 RI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.5182 1 0.6508 EP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.4501 1 0.7074 MH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.3909 1 0.7509 NP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.3395 1 0.7842 MH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.2949 1 0.8097 JS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.2561 1 0.8292 OK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.2224 1 0.8440 OS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1932 1 0.8553 IK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1678 1 0.8639 MR 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1457 1 0.8704 RJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1266 1 0.8754 KR 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 NJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0955 2 0.8928 PE 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 PM 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0720 2 0.9110 FE 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0625 2 0.9170 GM 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0543 2 0.9215 ID 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0472 3 0.9318 LL 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0410 3 0.9423 HD 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 ML 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 IG 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 FO 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 CG 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 FO 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 KF 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0153 3 0.9637 HN 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0133 4 0.9659 KF 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0115 3 0.9679 NN 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 DI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0087 6 0.9710 QQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 CI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 JQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 HH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 HP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 LH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 DP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0032 5 0.9799 KK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 LS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0024 7 0.9828 OK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0021 6 0.9843 DS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0018 5 0.9852 DJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0016 6 0.9860 ER 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0014 5 0.9866 RJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0012 7 0.9872 OR 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0010 7 0.9877 EN 0 19:57:24.130 ELN_MA (GBPUSD,D1) IS 0 19:57:24.130 ELN_MA (GBPUSD,D1) Descending lambda path... EI 0 19:57:24.130 ELN_MA (GBPUSD,D1) 1.0487 1 0.0005 EP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.9108 1 0.2023 RH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.7910 1 0.3600 LP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.6870 1 0.4827 PH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.5967 1 0.5778 QS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.5182 1 0.6513 OK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.4501 1 0.7079 PS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.3909 1 0.7514 PK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.3395 1 0.7847 OR 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.2949 1 0.8102 DJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.2561 1 0.8297 ER 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.2224 1 0.8445 GJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1932 1 0.8558 JE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1678 1 0.8644 GM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1457 1 0.8709 LE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1266 1 0.8759 JM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1099 2 0.8808 DD 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0955 2 0.8929 OL 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0829 2 0.9033 HD 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0720 2 0.9113 FL 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0625 2 0.9173 FG 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0543 2 0.9219 RO 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0472 3 0.9312 MG 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0410 3 0.9418 JO 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0356 2 0.9473 EF 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0309 2 0.9506 GN 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0268 2 0.9531 QF 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0233 4 0.9559 HN 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0202 4 0.9589 QI 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0176 3 0.9613 HQ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0153 3 0.9639 RI 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 OQ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0115 3 0.9681 JH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0100 5 0.9695 KP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0087 4 0.9709 NH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0075 4 0.9738 CP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0066 5 0.9752 NK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0057 5 0.9764 CS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0049 4 0.9774 RK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0043 5 0.9783 LS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0037 4 0.9792 GJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0032 5 0.9801 NR 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 PJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 RR 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0021 7 0.9842 KM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0018 6 0.9853 EE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0016 7 0.9861 NM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0014 6 0.9867 OE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0012 6 0.9873 KL 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0010 7 0.9878 HG 0 19:57:24.146 ELN_MA (GBPUSD,D1) PG 0 19:57:24.146 ELN_MA (GBPUSD,D1) OptimizeLambda ending with best lambda=0.001048683 explained=0.987563916
Notice that when lambda is at its maximum, the number of active predictors is zero, and this value increases as lambda is decreased at each iteration. The number of selected predictors increases or decreases as the algorithm decides which lambda value is best. The resulting model ends up discarding a few more indicator values it deems unnecessary.
PE 0 19:57:24.177 ELN_MA (GBPUSD,D1) optimal lambda 0.00104868 GM 0 19:57:24.287 ELN_MA (GBPUSD,D1) explained variance 0.9871030095923066 DK 0 19:57:24.287 ELN_MA (GBPUSD,D1) NS 0 19:57:24.287 ELN_MA (GBPUSD,D1) 2 , 1 ,1.70372722883263016946e+00 RG 0 19:57:24.287 ELN_MA (GBPUSD,D1) 4 , 2 ,-1.67483731989555195696e+00 QO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 6 , 3 ,1.07905337481491181428e+00 PQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 8 , 4 ,0.00000000000000000000e+00 HJ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 10 , 5 ,0.00000000000000000000e+00 LN 0 19:57:24.287 ELN_MA (GBPUSD,D1) 12 , 6 ,-1.81038986082938974098e-01 DF 0 19:57:24.287 ELN_MA (GBPUSD,D1) 14 , 7 ,0.00000000000000000000e+00 OH 0 19:57:24.287 ELN_MA (GBPUSD,D1) 16 , 8 ,0.00000000000000000000e+00 FR 0 19:57:24.287 ELN_MA (GBPUSD,D1) 18 , 9 ,0.00000000000000000000e+00 CE 0 19:57:24.287 ELN_MA (GBPUSD,D1) 20 , 10 ,0.00000000000000000000e+00 FO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 22 , 11 ,0.00000000000000000000e+00 IQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 24 , 12 ,0.00000000000000000000e+00 HK 0 19:57:24.287 ELN_MA (GBPUSD,D1) 26 , 13 ,0.00000000000000000000e+00 OM 0 19:57:24.287 ELN_MA (GBPUSD,D1) 28 , 14 ,0.00000000000000000000e+00 GG 0 19:57:24.287 ELN_MA (GBPUSD,D1) 30 , 15 ,0.00000000000000000000e+00 HI 0 19:57:24.287 ELN_MA (GBPUSD,D1) 32 , 16 ,0.00000000000000000000e+00 ES 0 19:57:24.287 ELN_MA (GBPUSD,D1) 34 , 17 ,0.00000000000000000000e+00 RE 0 19:57:24.287 ELN_MA (GBPUSD,D1) 36 , 18 ,0.00000000000000000000e+00 CO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 38 , 19 ,0.00000000000000000000e+00 HQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 40 , 20 ,0.00000000000000000000e+00 IK 0 19:57:24.287 ELN_MA (GBPUSD,D1) 42 , 21 ,0.00000000000000000000e+00 FM 0 19:57:24.287 ELN_MA (GBPUSD,D1) 44 , 22 ,0.00000000000000000000e+00 CG 0 19:57:24.287 ELN_MA (GBPUSD,D1) 46 , 23 ,0.00000000000000000000e+00 LI 0 19:57:24.287 ELN_MA (GBPUSD,D1) 48 , 24 ,0.00000000000000000000e+00 DS 0 19:57:24.287 ELN_MA (GBPUSD,D1) 50 , 25 ,0.00000000000000000000e+00 CE 0 19:57:24.287 ELN_MA (GBPUSD,D1) 52 , 26 ,0.00000000000000000000e+00 JO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 54 , 27 ,0.00000000000000000000e+00 MQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 56 , 28 ,0.00000000000000000000e+00 HK 0 19:57:24.287 ELN_MA (GBPUSD,D1) 58 , 29 ,0.00000000000000000000e+00 IM 0 19:57:24.287 ELN_MA (GBPUSD,D1) 60 , 30 ,0.00000000000000000000e+00 PD 0 19:57:24.287 ELN_MA (GBPUSD,D1) OOS total return = 3.42215 (2963.528 percent)
Conclusion
Elastic net regression is quite remarkable in terms of its capabilities. But its no magic bullet, as there are a number of critical variables used to define the model, that require specification. Besides the type of regularization that needs to be selected, the user still has to grapple with other aspects such as the convergence criterion. Despite these drawbacks, it cannot be denied that it is a useful tool have.| FileName | Description |
|---|---|
| MQL5\Indicators\LogPrices.mq5 | an indicator to log tranform raw prices, its handle can be passed to other indicator call. |
| MQL5\Include\CoordinateDescent.mqh | include file containing definition of CCoordinateDescent class as well as OptimizeLambda() function |
| MQL5\Scripts\ELN_MA.mq5 | This is an example of a script that applies the elastic net to build a predictive model from multiple moving average indicators. |
Attached files |
CoordinateDescent.mqh
(29.25 KB)
LogPrices.mq5
(1.83 KB)
ELN_MA.mq5
(10.25 KB)
mql5files.zip
(11.67 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
Go to discussion
Neural networks made easy (Part 37): Sparse Attention
In the previous article, we discussed relational models which use attention mechanisms in their architecture. One of the specific features of these models is the intensive utilization of computing resources. In this article, we will consider one of the mechanisms for reducing the number of computational operations inside the Self-Attention block. This will increase the general performance of the model.
Understanding order placement in MQL5
When creating any trading system, there is a task we need to deal with effectively. This task is order placement or to let the created trading system deal with orders automatically because it is crucial in any trading system. So, you will find in this article most of the topics that you need to understand about this task to create your trading system in terms of order placement effectively.
Developing a Replay System — Market simulation (Part 06): First improvements (I)
In this article, we will begin to stabilize the entire system, without which we might not be able to proceed to the next steps.
Category Theory in MQL5 (Part 19): Naturality Square Induction
We continue our look at natural transformations by considering naturality square induction. Slight restraints on multicurrency implementation for experts assembled with the MQL5 wizard mean we are showcasing our data classification abilities with a script. Principle applications considered are price change classification and thus its forecasting.
You are missing trading opportunities:
- Free trading apps
- Free Forex VPS for 24 hours
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register