
모집단 최적화 알고리즘: 인공 꿀벌 군집(ABC)
콘텐츠
1. 소개
사회적 곤충은 고도로 진화한 생물로서 개별 곤충들이 수행하지 못하는 여러 가지 복잡한 작업을 수행합니다. 의사소통, 복잡한 둥지 건설, 환경 제어, 보호 및 분업은 꿀벌이 사회적 군집에서 번성하기 위해서 진화하게 된 행동 중 일부입니다.
꿀벌은 군집 생활을 하며 최적의 솔루션을 찾는 데 탁월한 능력을 발휘합니다. 꿀벌은 벌집 근처에서 꿀과 꽃가루를 모으기 위해 꽃 무리를 찾습니다. 때로는 검색 반경이 최대 수 킬로미터까지 늘어날 수 있습니다. 귀환하는 꿀벌은 즉흥적인 춤을 추어 발견한 것들을 보고합니다.
언뜻 보기에 이것이 불가능 해 보이지만 리드미컬 한 움직임을 통해 지리적 위치에 대한 정보를 서로에게 전달할 수 있습니다. 꿀벌은 형제들의 춤의 강도에 따라 특정 지점에서 꽃의 수와 예상 가능한 꿀의 양에 대한 결론을 도출합니다. 잠재적인 먹거리가 많을수록 춤이 더 활발해집니다. 이 특이한 현상은 곤충 연구자 칼 폰 프리쉬가 20세기 중반에 발견했습니다.
수년 동안 꿀벌 탐색 방법은 생물학자들에 의해서만 연구되었습니다. 그러나 새로운 최적화 알고리즘을 개발하면서 군집 행동을 적용하는 것에 대한 관심이 높아지고 있었습니다. 2005년 데르비스 카라보가 교수는 연구 결과에 관심을 갖게 되었습니다. 그는 과학 논문을 발표하고 꿀벌의 춤에서 영감을 얻은 군집 지능 모델을 최초로 설명했습니다. 이 모델을 인공 꿀벌 군집이라고 불렀습니다.
2. 알고리즘 설명
인공 꿀벌 군집은 벌집에서 벌을 관리하는 원칙과 지역 탐사의 규칙 등에서 서로 다른 여러 가지가 있습니다. 이 글에서는 고전적인 버전의 알고리즘에 대한 저의 해석에 대해 다루어 보겠습니다.
알고리즘의 아이디어는 꿀벌이 꿀을 최대한 많이 얻을 수 있는 장소를 찾을 때 발생하는 벌의 행동에 기반합니다. 먼저 모든 꿀벌은 벌집에서 무작위의 방향으로 날아가 정찰병의 역할을 하며 꿀이 있는 곳을 찾으려고 노력합니다. 그 후 꿀벌은 벌집으로 돌아와 특별한 방법으로 다른 벌들에게 꿀을 어디서 얼마나 찾았는지를 알려줍니다.
일벌은 발견된 지역으로 보내집니다. 이 지역에서 꿀이 더 많이 발견될수록 더 많은 꿀벌이 그 방향으로 날아갑니다. 정찰대는 다시 다른 지역을 찾기 위해 날아가지만 이미 발견한 지역 근처에 있습니다. 따라서 모든 꿀벌은 꿀을 모으는 일벌과 새로운 지역을 탐험하는 정찰벌의 두 가지 유형으로 나뉩니다. 꿀을 수집하는 지역에는 꿀의 양에 해당하는 값이 있습니다. 순위가 낮은 지역은 있는 순위가 높은 지역에 가까이 위치합니다. 이들은 지역 중앙을 통과하는 선을 따라 위치합니다.
지역별 일벌의 분포는 그림 1에서 개략적으로 시각화 할 수 있습니다.

그림 1. 지역 순위에 따른 지역 내 꿀벌 수
구역 1은 등급이 높고 꿀이 가장 많이 함유되어 있어 더 많은 꿀벌이 날아드는 경향이 있습니다. 꿀벌의 수에 따라 4번 지역의 순위(값)가 가장 낮다는 것을 시각적으로 확인할 수 있습니다. 각 지역의 가치에 대한 정보는 꿀벌들이 특별한 춤의 형태로 보고합니다. 각 벌집에는 해당 지역의 꿀의 방향과 양이 프로그래밍 된 춤이 있습니다.
지구에서 극단의 위치가 꿀이 가장 많은 지역이고 그러한 지역이 하나만 있다고 가정해 봅시다. 비록 양은 적지만 다른 곳에도 꿀이 있습니다. 꿀벌은 다차원 공간에 서식하며 각 좌표는 최적화해야 하는 함수의 매개변수 하나를 나타냅니다. 찾은 꿀의 양은 우리가 글로벌 최대값을 찾고 있는 경우라면 여기서 목적 함수의 값입니다. 글로벌 최소값을 찾고 있다면 목적 함수에 -1을 곱하는 것으로 충분합니다.
꿀을 수집 하는 지역은 특정한 값을 가지기 때문에 가장 높은 등급을 가진 지역만 꿀이 가장 많이 모이는 지점으로 이동할 수 있는 권한(중앙 이동)을 갖습니다. 순위가 낮은 지역은 집중도가 가장 높은 곳의 중앙으로 이동하고 순위가 높은 지역과 교차되는지 비교 됩니다. 이러한 방식으로 좁은 공간에 꿀벌이 집중되는 것을 방지하고 일벌이 최대한 효율적으로 탐색 공간을 찾을 수 있게 하여 먹이가 고갈되는 것을 방지합니다. 최적화 측면에서 보면 이를 통해 벌들이 로컬 극한값에 갇히는 것을 방지하거나 최소화할 수 있습니다. 먹이를 얻는 지역이 분산되고 벌들은 순위를 따라 서로 상대적으로 이동한 후에는 꿀벌 정찰대가 해당 지역을 추가로 조사합니다.
많은 양봉가들이 정찰 꿀벌을 무작위의 검색 공간으로 보내는 것을 권장하지만 제 경험에 따르면 이러한 '정찰'의 실제 가치는 0에 가까우며 1차원과 2차원에서만 유용합니다. 즉 다차원 공간에서 자유도는 기하학적으로 증가하며 더 가치 있는 꿀이 있는 장소를 우연히 발견하기가 엄청나게 어렵습니다. 벌집을 만드는 자원은 낭비될 것입니다. 이미 알려진 검색 지역 가까이에 정찰벌을 보내 좌표가 흩어지지 않게 하고 꿀 공급원에 더 집중되도록 하는 것이 훨씬 더 유용합니다.
지역이 교차하는 경우 지역이 테두리에만 닿도록 중심을 이동해야 합니다. 이는 그림 2에 나와 있습니다.
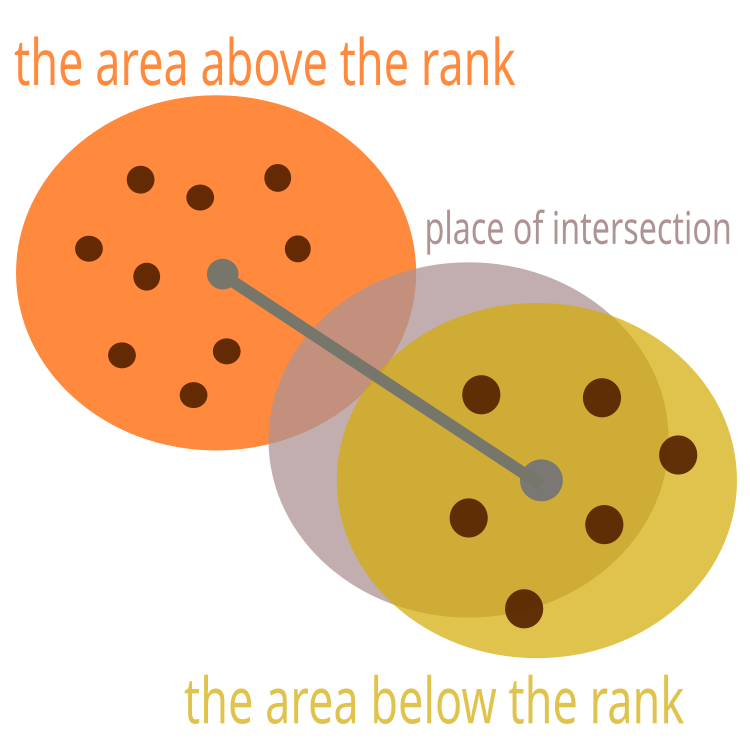
그림 2. 순위가 낮은 지역은 옮겨져야 합니다.
지역의 순위는 고정적으로 설정되는 것이 아니라 동적으로 형성됩니다. 정찰 벌이 발견한 것들은 그 벌이 날아간 지역에 할당됩니다. 더 귀중한 식량 공급원이 발견되면 해당 지역의 중심이 그곳으로 옮겨 집니다. 그곳은 꿀 수집을 위한 최고의 센터가 될 수도 있습니다. 이제 나머지 지역은 해당 지역을 기준으로 이동합니다. 즉 랭크 체인을 따라 상대적으로 이동하게 됩니다.
꿀벌의 춤이라고 하는 정보 전달 방법은 벌집 전략의 필수 요소입니다. 벌떼의 가용 자원을 지역에 가장 합리적으로 분배해야 하므로 보내지는 꿀벌의 수는 각 지역의 가치에 비례해야 합니다. 즉 동일한 수의 꿀벌들이 동일한 가치의 지역으로 보내지게 됩니다.
이제 알고리즘 자체로 넘어가 보겠습니다. 실행 단계는 다음과 같습니다:
- 모든 꿀벌은 정찰대원의 역할로 탐색 공간을 따라 무작위로 날아갑니다.
- 각 꿀벌로부터 받은 꿀의 양을 측정합니다.
- 꿀벌 분류.
- 꿀벌로부터 얻은 꿀의 양에 따라 지역을 할당합니다.
- 일벌을 해당 지역으로 보내기. 해당 지역에 꿀이 많을수록 더 많은 꿀벌을 보낼 수 있습니다.
- 무작위로 선택된 지역 근처에 정찰 벌을 보냅니다.
- 각 꿀벌로부터 받은 꿀의 양을 측정합니다.
- 꿀의 양에 따라 지역의 순위를 매깁니다.
- 중지하는 기준이 충족될 때까지 4를 반복합니다.
시각적으로 쉽게 이해할 수 있도록 그림 3과 같이 알고리즘의 블록 다이어그램을 만들어 보겠습니다.

그림 3. 알고리즘 블록 다이어그램
꿀벌 군집 알고리즘 코드에 대해 좀 더 자세히 설명하겠습니다.
꿀벌은 알고리즘의 기본 논리 단위입니다. 이를 구조로 설명할 수 있습니다. 아시다시피 꿀벌의 위치는 좌표, 꿀을 채취한 지역의 근방, 꿀의 양에 따라 설정됩니다. 그러면 벌집의 벌들이 배열로 표시될 것입니다. 각각의 배열은 인덱스로 액세스할 수 있습니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Bee { double c []; //coordinates int aInd; //area index double n; //nectar }; //——————————————————————————————————————————————————————————————————————————————
두 번째로 더 큰 논리 단위는 꿀 수집 지역입니다. 이 지역은 꿀의 농도가 가장 높은 중심과 지점, 그리고 그 지역의 가치를 결정하는 꿀의 양에 의해 정의됩니다. 가장 높은 등급(목록에서 첫 번째)의 지역에서는 중심 좌표와 꿀의 농도가 가장 높은 좌표가 일치합니다. 목록에서 두 번째 이하 순위에 있는 지역의 경우에는 순위가 바뀌었기 때문에 일치하지 않을 수 있습니다. 지역 초기화는 꿀의 양의 지표를 재설정하고 최적화된 함수의 해당 매개 변수의 수에 좌표를 배포하는 것으로 마무리됩니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Area { void Init (int coordinatesNumber) { n = -DBL_MAX; ArrayResize (cC, coordinatesNumber); ArrayResize (cB, coordinatesNumber); } double cC []; //center coordinates double cB []; //best coordinates double n; //nectarAmount }; //——————————————————————————————————————————————————————————————————————————————
이제 꿀벌의 춤을 구조로 설명하고 그 배열은 지역의 수에 해당한다고 가정해 봅시다.
//—————————————————————————————————————————————————————————————————————————————— struct S_BeeDance { double start; double end; }; //——————————————————————————————————————————————————————————————————————————————
벌집을 검색 지역, 꿀벌, 최적의 좌표, 모든 반복에서 발견되는 꿀의 최대량을 설정하는 클래스로 설명하겠습니다. 또한 꿀벌과 지역을 정렬하는 데 필요한 모든 메서드와 꿀벌과 지역을 서로 상대적으로 이동하는 메서드도 여기에서 정의됩니다. 여기에서는 이전 알고리즘에서 이미 익숙한 함수 선언을 볼 수 있습니다: 균등하게 분포된 무작위 숫자 생성, 범위로 스케일링하고 단계가 있는 범위에서 숫자를 선택하는 것 등이 있습니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ABC //Bees Hive { //============================================================================ public: S_Area areas []; //nectar collection areas public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Bee bees []; //all the bees of the hive public: double cB []; //best coordinates public: double nB; //nectar of the best coordinates public: void InitHive (const int coordinatesP, //number of opt. parameters const int beesNumberP, //bees number const int workerBeesNumberP, //worker bees number const int areasNumberP, //areas number const double collectionRadiusP, //collection radius const double scoutAreaRadiusP); //scout area radius public: void TasksForBees (); public: void CollectingNectar (); //============================================================================ private: void BeeFlight (double &cC [] , S_Bee &bee); private: void ScoutBeeFlight (double &cC [] , S_Bee &bee); private: void MarkUpAreas (); private: void SortingBees (); private: void SortingAreas (); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: int coordinates; //coordinates number private: int beesNumber; //the number of all bees private: int workerBeesNumber; //worker bees number private: int areasNumber; //areas number private: S_Bee beesT []; //temporary, for sorting private: S_Area areasT []; //temporary, for sorting private: int indA []; //array for indexes when sorting private: double valA []; //array for nectar values when sorting private: int indB []; //array for indexes when sorting private: double valB []; //array for nectar values when sorting private: double areasRadius []; //radius for each coordinate private: double scoutRadius []; //scout radius for each coordinate private: double collectionRadius; //collection radius private: double scoutAreaRadius; //scout area radius private: double hypersphereRadius; //hypersphere radius private: double distHyperspCenters; //distance hyperspheres centers private: double scoutHyperspRadius; //scout hypersphere radius private: bool scouting; //scouting flag private: S_BeeDance beeDance []; //bee dance }; //——————————————————————————————————————————————————————————————————————————————
새로운 최적화는 반드시 클래스 초기화부터 시작해야 합니다. 꿀의 양은 벌집 전체와 개별 꿀벌 및 지역에 대해 재설정됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABC::InitHive (const int coordinatesP, //number of opt. parameters const int beesNumberP, //bees number const int workerBeesNumberP, //worker bees number const int areasNumberP, //areas number const double collectionRadiusP, //collection radius const double scoutAreaRadiusP) //scout area radius { MathSrand (GetTickCount ()); scouting = false; nB = -DBL_MAX; coordinates = coordinatesP; beesNumber = beesNumberP; workerBeesNumber = workerBeesNumberP; areasNumber = areasNumberP < 3 ? 3 : areasNumberP; collectionRadius = collectionRadiusP; //collection radius scoutAreaRadius = scoutAreaRadiusP; //scout area radius ArrayResize (areas, areasNumber); ArrayResize (areasT, areasNumber); for (int i = 0; i < areasNumber; i++) { areas [i].Init (coordinates); areasT [i].Init (coordinates); } ArrayResize (beeDance, areasNumber); ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (indA, areasNumber); ArrayResize (valA, areasNumber); ArrayResize (areasRadius, coordinates); ArrayResize (scoutRadius, coordinates); for (int i = 0; i < coordinates; i++) { areasRadius [i] = (rangeMax [i] - rangeMin [i]) * collectionRadius; scoutRadius [i] = (rangeMax [i] - rangeMin [i]) * scoutAreaRadius; } double sqr = 0.0; for (int i = 0; i < coordinates; i++) sqr += areasRadius [i] * areasRadius [i]; hypersphereRadius = MathSqrt (sqr) * collectionRadius; distHyperspCenters = hypersphereRadius * 2.0; sqr = 0.0; for (int i = 0; i < coordinates; i++) sqr += scoutRadius [i] * scoutRadius [i]; scoutHyperspRadius = MathSqrt (sqr) * scoutAreaRadius; ArrayResize (indB, beesNumber); ArrayResize (valB, beesNumber); ArrayResize (bees, beesNumber); ArrayResize (beesT, beesNumber); for (int i = 0; i < beesNumber; i++) { ArrayResize (bees [i].c, coordinates); ArrayResize (beesT [i].c, coordinates); bees [i].n = -DBL_MAX; beesT [i].n = -DBL_MAX; } } //——————————————————————————————————————————————————————————————————————————————
가장 간단하고 개방적인 클래스 메서드는 꿀벌에게 작업을 분배하는 것입니다. 여기서는 모든 것이 간단합니다. 지역이 아직 탐험 되지 않은 경우 전체 벌집의 꿀의 값을 재설정하고 지역 표시를 시작합니다. 적합도 함수의 값을 얻을 때까지 각 에포크에서 메서드를 호출합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABC::TasksForBees () { if (!scouting) { nB = -DBL_MAX; } MarkUpAreas (); } //——————————————————————————————————————————————————————————————————————————————
두 번째 공개 메서드는 모든 에포크에서 호출됩니다. 피트니스 함수의 값을 가져온 후에 실행해야 합니다. 이 경우 아직 탐사가 수행되지 않은 경우 꿀의 값에 따라 꿀벌을 정렬하고 목록에 있는 첫 번째 꿀벌의 좌표와 꿀의 양을 해당 지역에 복사합니다. 이미 탐사가 진행된 경우 결과가 개선되었다면 꿀을 채취한 지역의 좌표와 꿀의 양을 복사합니다. 또한 전체 벌집에 대한 최상의 결과를 업데이트합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABC::CollectingNectar () { if (!scouting) { SortingBees (); for (int a = 0; a <areasNumber; a++) { ArrayCopy (areas [a].cB, bees [a].c, 0, 0, WHOLE_ARRAY); areas [a].n = bees [a].n; } scouting = true; } else { //transfer the nectar to the hive--------------------------------------------- for (int b = 0; b < beesNumber; b++) { if (bees [b].n > areas [bees [b].aInd].n) { ArrayCopy (areas [bees [b].aInd].cB, bees [b].c, 0, 0, WHOLE_ARRAY); areas [bees [b].aInd].n = bees [b].n; } if (bees [b].n > nB) { ArrayCopy (cB, bees [b].c, 0, 0, WHOLE_ARRAY); nB = bees [b].n; } } SortingAreas (); } } //——————————————————————————————————————————————————————————————————————————————
MarkUpAreas () 메서드는 자세히 살펴볼 가치가 있습니다. 이제 코드를 여러 부분으로 나눠 보겠습니다.
지역을 탐사하기 전에 꿀을 채취할 꽃에 대한 정보가 없는 경우 모든 꿀벌을 보내 예비 탐사를 수행합니다. 이 단계에서 모든 꿀벌은 정찰병의 역할을 합니다. 꿀에 대한 정보가 없으므로 정찰대를 무작위의 방향으로 보내 좌표의 범위에 고르게 분포된 난수를 생성합니다.
//if the areas is not scouting - send all the bees to scouting---------------- if (!scouting) { for (int b = 0; b < beesNumber; b++) { for (int c = 0; c < coordinates; c++) { bees [b].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); bees [b].c [c] = SeInDiSp (bees [b].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } }
지역이 탐색된 후에는 꿀의 최대 농도 좌표를 해당 지역의 중앙에 복사해야 합니다. 즉 해당 지역을 더 나은 곳으로 이동해야 합니다. 이 작업을 수행한 후에는 해당 지역이 더 높은 등급의 지역과 교차되지 않는지를 확인해야 합니다. 중심 사이의 거리를 측정하여 지역의 교차점을 확인할 수 있습니다. 중심 사이의 거리가 두 반지름(알고리즘 매개변수 중 하나) 미만인 경우 지역이 교차합니다. 교차점이 감지되면 해당 지역은 반경이 두 개인 지점으로 이동하고 가장 좋은 결과를 얻은 좌표(최대 꿀 농도 좌표)는 같은 위치에 유지됩니다. 따라서 해당 지역은 끊임없이 움직입니다. 최고의 지역은 나머지 지역이 이동하게 되도록 영향을 미칩니다. 나머지 지역은 지역이 이동하는 동안 더 풍부한 식량 공급원에 도달하여 다음 메서드에서 분류 후 최고가 될 수 있습니다.
for (int s = 0; s < areasNumber; s++) { //move the center of the area to the best point in with more nectar------- ArrayCopy (areas [s].cC, areas [s].cB, 0, 0, WHOLE_ARRAY); //ordinary area----------------------------------------------------------- if (s != 0) { //check if there is no intersection of a region with a region of higher rank //measure the distance from the centers of the regions double centersDistance = 0.0; for (int c = 0; c < coordinates; c++) centersDistance += pow (areas [s].cC [c] - areas [s - 1].cC [c], 2.0); centersDistance = MathSqrt (centersDistance); //the areas intersect, then need to move the current area if (centersDistance < distHyperspCenters) { double incrementFactor = (distHyperspCenters - centersDistance) / centersDistance; double coordDistance = 0.0; for (int c = 0; c < coordinates; c++) { coordDistance = areas [s].cC [c] - areas [s - 1].cC [c]; areas [s].cC [c] = areas [s].cC [c] + (coordDistance * incrementFactor); areas [s].cC [c] = SeInDiSp (areas [s].cC [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } }
이곳에서 꿀벌들의 춤이 펼쳐집니다. 꿀의 방향과 양에 대한 정보를 사용하고 무작위 요소를 적용하여 다음번의 반복에서 꿀벌이 특정 지역을 선택할 확률이 해당 지역의 꿀의 양에 비례하도록 하는 식으로 난수의 분포 지역을 표시합니다. 간단히 말해 숫자 선에 각 지역의 꿀의 값과 최악의 지역의 차이에 해당하는 길이를 가진 세그먼트를 표시합니다.
//send bees to the marked areas----------------------------------------------- double r = 0.0; beeDance [0].start = bees [0].n; beeDance [0].end = beeDance [0].start + (bees [0].n - bees [areasNumber - 1].n); for (int a = 1; a < areasNumber; a++) { if (a != areasNumber - 1) { beeDance [a].start = beeDance [a - 1].end; beeDance [a].end = beeDance [a ].start + (bees [a].n - bees [areasNumber - 1].n); } else { beeDance [a].start = beeDance [a - 1].end; beeDance [a].end = beeDance [a ].start + (bees [a - 1].n - bees [a].n) * 0.1; } }
메서드 코드의 이 부분에서는 일벌의 춤에 따른 확률에 따라 지역을 무작위로 선택합니다. 이를 위해 숫자 라인에 춤으로 표시하여 만든 난수를 범위에 생성하도록 합니다. 정찰병의 경우 어느 지역에서든 그 근처에서 동일한 확률로 날아다니기 때문에 춤은 중요하지 않으며 이에 따라 꿀벌 전략의 탐색 기능이 더 넓어집니다. 자연에서와 마찬가지로 각 벌집의 벌들은 역할을 수행하면서 일정한 가치를 지니고 있습니다.
for (int b = 0; b < beesNumber; b++) { if (b < workerBeesNumber) { r = RNDfromCI(beeDance [0].start, beeDance [areasNumber - 1].end); for (int a = 0; a < areasNumber; a++) { if (beeDance [a].start <= r && r < beeDance [a].end) { bees [b].aInd = a; break; } } BeeFlight (areas [bees [b].aInd].cC, bees [b]); } else { //choose the area to send the bees there r = RNDfromCI (0.0, areasNumber - 1); bees [b].aInd = (int)r; //area index ScoutBeeFlight (areas [bees [b].aInd].cC, bees [b]); } }
이 비공개 메서드는 꿀벌의 비행을 구현합니다. 언뜻 보기에는 이해하기 어렵고 복잡해 보이지만 여기에서는 모든 것이 간단합니다. 꿀벌은 중앙에 가까워질수록 세제곱의 확률로 이동합니다. 따라서 확률은 지역 중심에서 경계선까지 감소합니다. 이 위치는 단지 지역의 중심이며 앞서 찾은 최적의 위치가 아니라는 점을 명심하세요. 이 간단한 행동에서도 꿀벌의 전략이 나타나며 이와 같이 꿀벌들은 새로운 식량원을 지속적으로 찾을 수 있습니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABC::BeeFlight (double &cC [] , S_Bee &bee) { double r = 0.0; for (int c = 0; c < coordinates; c++) { r = RNDfromCI (0.0, 1.0); r = r * r * r; r = Scale (r, 0.0, 1.0, 0.0, areasRadius [c], false); r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0; bee.c [c] = SeInDiSp (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
이전 메서드와 달리 여기에서는 정찰 꿀벌의 비행을 설명합니다. 꿀벌은 알고리즘의 설정에서 지정된 반경의 밖으로 날아갑니다. 설정은 동일하지만 좌표 범위가 다를 수 있기 때문에 클래스가 초기화될 때 반경이 미리 계산됩니다. 그러므로 반경이 적절해야 합니다. 정찰 벌이 날아가도록 하려면 해당 지역의 반경에서 해당 지역의 반경과 탐사 반경을 합한 범위에서 난수를 생성한 다음 결과값을 해당 지역의 중심에 더하면 됩니다. 이렇게 간단한 방법으로 정찰 꿀벌은 우연히 해당 지역의 근처에 있을 것이며 좌표는 검색 공간의 전체에 흩어지지 않을 것입니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABC::ScoutBeeFlight (double &cC [] , S_Bee &bee) { double r = 0.0; for (int c = 0; c < coordinates; c++) { r = RNDfromCI (areasRadius [c], areasRadius [c] + scoutRadius [c]); r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0; bee.c [c] = SeInDiSp (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
알고리즘에는 꿀벌 정렬과 지역 정렬이라는 두 가지 구체적인 메서드가 있습니다. 이들을 설명하는 것은 의미가 없으며 단순한 버블 정렬일 뿐입니다. 이 메서드는 모든 정렬 방법 중 최고의 속도를 제공하면서 특정 작업에 맞게 간단하고 쉽게 수정할 수 있기 때문에 저는 이 메서드를 거의 모든 최적화 알고리즘(정렬이 필요한 경우)에서 사용합니다.
//—————————————————————————————————————————————————————————————————————————————— //Sorting of bees void C_AO_ABC::SortingBees () //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— //Sorting of areas void C_AO_ABC::SortingAreas () //——————————————————————————————————————————————————————————————————————————————
이제 살펴본 모든 코드를 모아 컴파일할 차례입니다. 테스트 스탠드를 실행하면 꿀벌 알고리즘이 어떻게 동작하는지를 보여주는 다음과 같은 애니메이션을 볼 수 있습니다. 꿀벌은 구분된 지역에서 명확하게 관찰됩니다. 지역이 어떻게 서로 대체되는지 확인할 수 있습니다. 정확도와 특이한 "스웜"의 수는 알고리즘 설정에 따라 달라집니다.
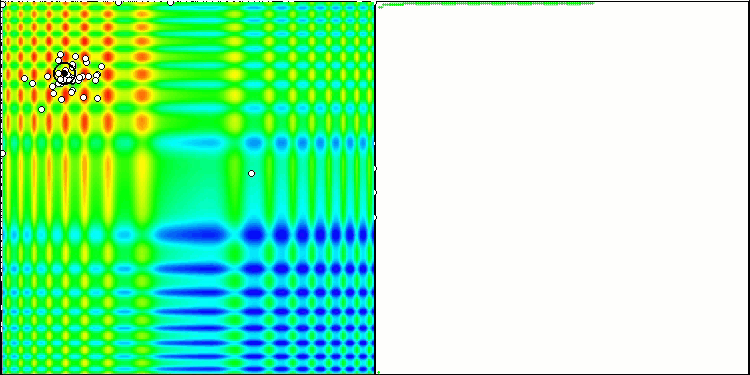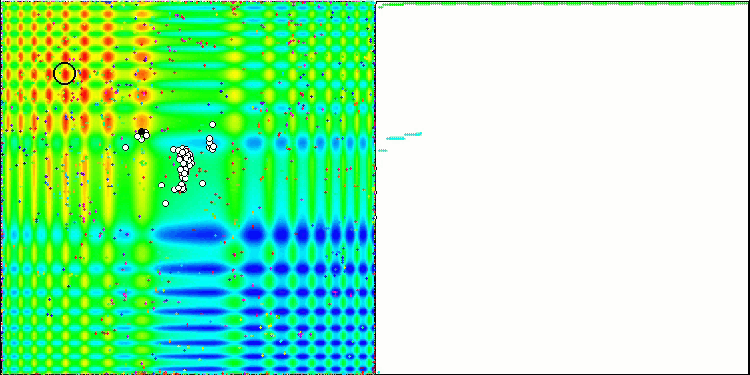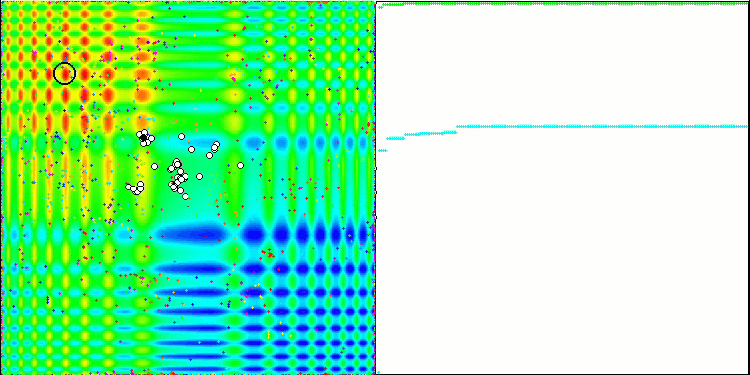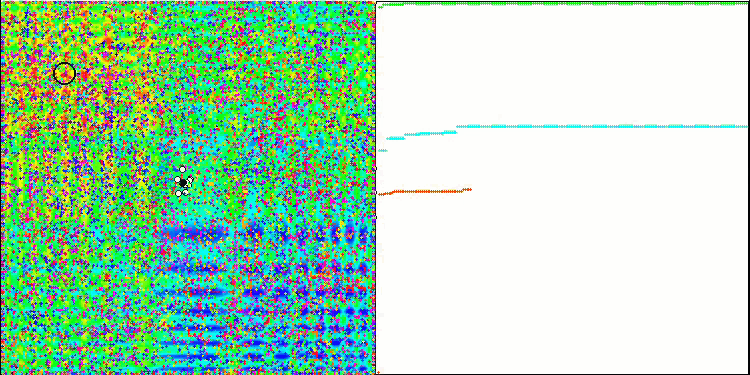
스킨 테스트 함수의 PSO.
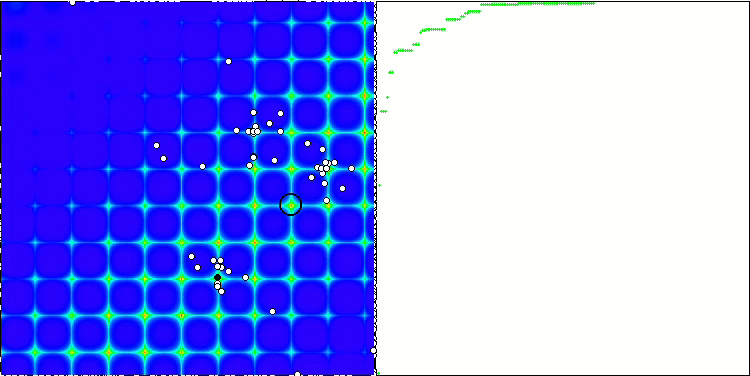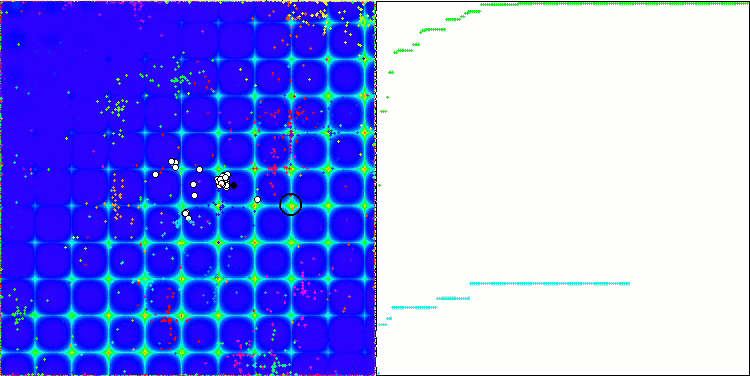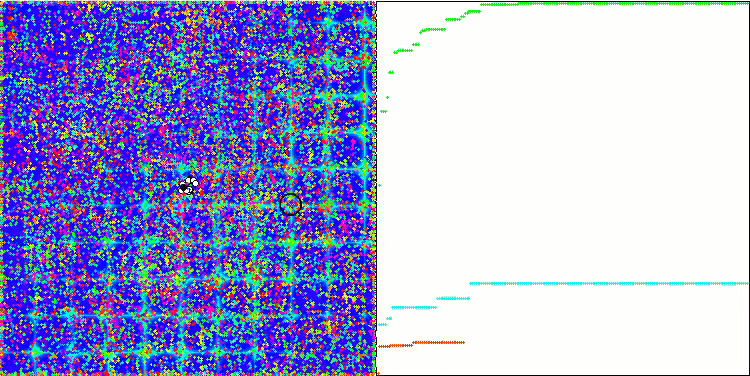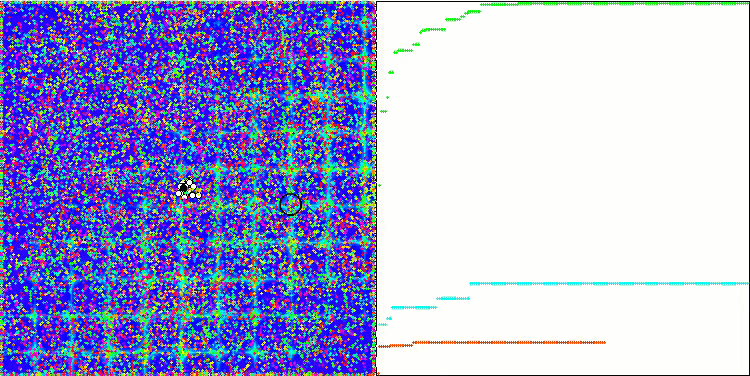
PSO의 포리스트 테스트 함수.
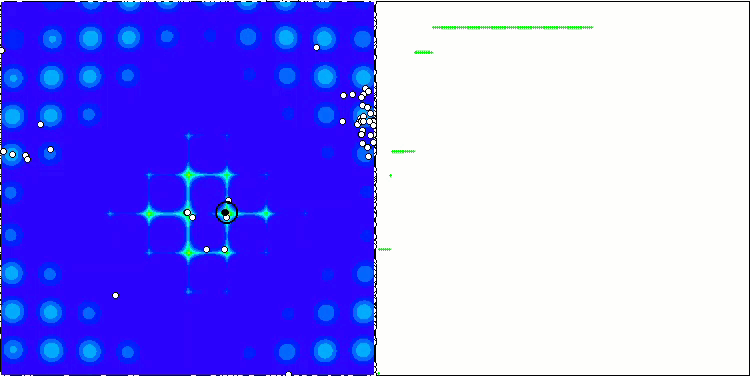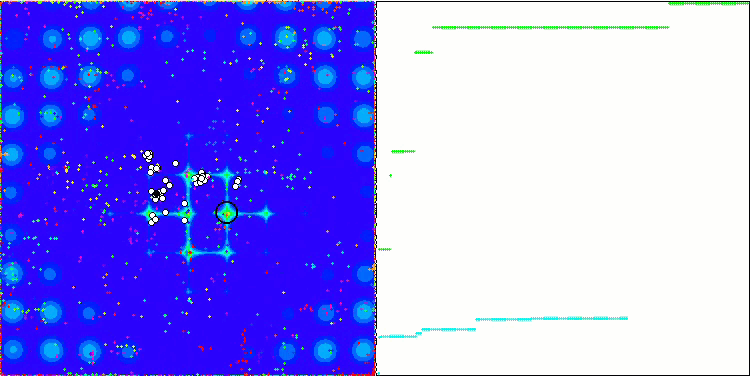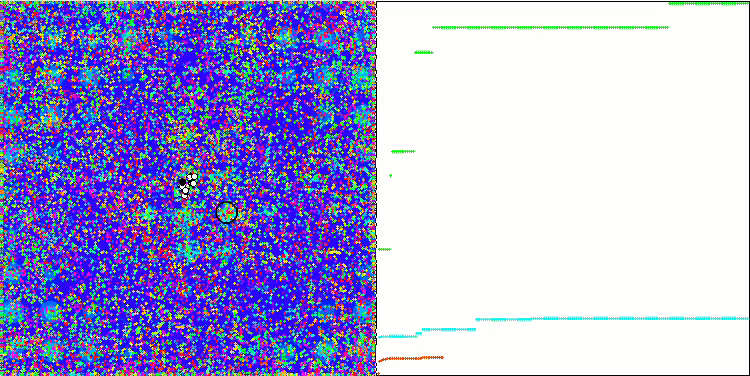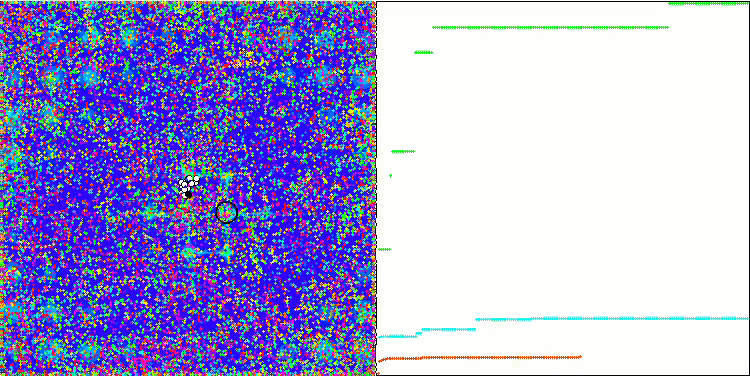
PSO의 메가시티 테스트 함수.
다음은 테스트 함수에서의 알고리즘 결과입니다:
2022.11.21 13:14:28.483 Test_AO_ABC1 (EURUSD,M1) 1 Skin's; Func runs 1000 result: 14.018634225602678; Dunc runs 10000 result: 14.06060189007221
2022.11.21 13:14:28.483 Test_AO_ABC1 (EURUSD,M1) Score1: 0.99772; Score2: 1.00000
2022.11.21 13:14:50.310 Test_AO_ABC1 (EURUSD,M1) 20 Skin's; Func runs 1000 result: 7.459929501115262; Func runs 10000 result: 8.320771456653533
2022.11.21 13:14:50.310 Test_AO_ABC1 (EURUSD,M1) Score1: 0.64085; Score2: 0.68769
2022.11.21 13:15:30.049 Test_AO_ABC1 (EURUSD,M1) 500 Skin's; Func runs 1000 result: 4.69267387794685; Func runs 10000 result: 4.838631770950824
2022.11.21 13:15:30.049 Test_AO_ABC1 (EURUSD,M1) Score1: 0.49029; Score2: 0.49823
2022.11.21 13:15:30.049 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:15:51.880 Test_AO_ABC1 (EURUSD,M1) 1 Forest's; Func runs 1000 result: 15.063567301715784; Func runs 10000 result: 15.912087696850861
2022.11.21 13:15:51.880 Test_AO_ABC1 (EURUSD,M1) Score1: 0.94435; Score2: 0.99755
2022.11.21 13:16:13.721 Test_AO_ABC1 (EURUSD,M1) 20 Forest's; Func runs 1000 result: 3.0207584941876133; Func runs 10000 result: 4.1918977577943295
2022.11.21 13:16:13.721 Test_AO_ABC1 (EURUSD,M1) Score1: 0.18937; Score2: 0.26279
2022.11.21 13:17:01.467 Test_AO_ABC1 (EURUSD,M1) 500 Forest's; Func runs 1000 result: 1.2004991531402736; Func runs 10000 result: 1.288357831462411
2022.11.21 13:17:01.467 Test_AO_ABC1 (EURUSD,M1) Score1: 0.07526; Score2: 0.08077
2022.11.21 13:17:01.467 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:17:23.227 Test_AO_ABC1 (EURUSD,M1) 1 Megacity's; Func runs 1000 result: 10.4; Func runs 10000 result: 15.0
2022.11.21 13:17:23.227 Test_AO_ABC1 (EURUSD,M1) Score1: 0.69333; Score2: 1.00000
2022.11.21 13:17:44.936 Test_AO_ABC1 (EURUSD,M1) 20 Megacity's; Func runs 1000 result: 1.5499999999999998; Func runs 10000 result: 2.31
2022.11.21 13:17:44.936 Test_AO_ABC1 (EURUSD,M1) Score1: 0.10333; Score2: 0.15400
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) 500 Megacity's; Func runs 1000 result: 0.6180000000000001; Func runs 10000 result: 0.6568
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) Score1: 0.04120; Score2: 0.04379
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) All score for C_AO_ABC: 0.49447371765340953
이 알고리즘은 두 가지 변수 테스트 함수 2개 각각에 대해 완전히 수렴했으며 이는 수렴을 나타내는 훌륭한 지표입니다. 나머지 결과를 평가하는 것은 시기상조입니다. 결과를 표에 정리하고 또 다른 최적화 알고리즘과 비교하여 결론을 도출하는 것이 좋습니다.
3. 수정된 버전
최적화 알고리즘을 개발하고 설계할 때는 항상 의문이 생깁니다: "알고리즘이 의도한 대로 작동할까, 아니면 코드 어딘가에 오류가 있지 않을까?" 확률적 검색 프로세스는 본질적으로 무작위이므로 알고리즘에 의해 최적화 결과가 도출된 것인지 아니면 어딘가에 오류가 있어 결과가 정말 무작위가 아닌 것인지가 명확하지 않습니다 제가 꿀벌 군집 알고리즘을 개발할 때도 비슷한 현상을 경험했습니다. 테스트 세트의 5가지 테스트 중 첫 번째 테스트에서 알고리즘은 검색을 시작한 지점에서 전혀 수렴을 시도하지 않고 멈췄습니다. 이 버그는 로직의 관점에서 볼 때 참으로 놀라운 방식으로 해결되었습니다. 하이브 클래스가 에포크 시작 전에 이미 사전 초기화되었음에도 불구하고 첫 번째 에포크에서 추가로 한 번 더 초기화하기만 하면 되었습니다(Test_AO_ABC.mq5의 string 142). 누군가 이 수수께끼를 풀 수 있다면 댓글에서 해결책을 들을 수 있기 바랍니다.
위와 같은 이유와 첫 번째 테스트의 만족스럽지 못한 결과(나중에 알고리즘 설정을 더 시험해야 한다는 것을 알게 되었지만) 때문에 저는 꿀벌 검색 전략을 변경하기 위한 아이디어를 떠올렸습니다. 원래 버전에서는 벌이 면적 값에 비례하여 날아갑니다. 새로운 알고리즘에서는 각 지역에 고정된 수의 꿀벌이 있어야 합니다. 즉 지역 등급에 관계없이 각 지역은 항상 같은 수의 벌을 보유합니다. 따라서 지역은 논리적으로 "꿀벌 떼"라는 개념으로 변형되었습니다.
이제 지역 구조 대신 다음과 같은 구조가 있습니다:
//—————————————————————————————————————————————————————————————————————————————— struct S_BeesSwarm { void Init (int coordinatesNumber, int beesNumber) { ArrayResize (bees, beesNumber); for (int i = 0; i < beesNumber; i++) { ArrayResize (bees [i].c, coordinatesNumber); bees [i].n = -DBL_MAX; } n = -DBL_MAX; ArrayResize (cC, coordinatesNumber); ArrayInitialize (cC, -DBL_MAX); } S_Bee bees []; //bees double cC []; //center coordinates double cB []; //best coordinates double n; //nectarAmount }; //——————————————————————————————————————————————————————————————————————————————
이 구조에는 초기화 함수도 있지만 bees[] 배열도 있습니다.
일반적으로 나머지 코드는 클래식 버전과 매우 유사하므로 여기에 너무 집중할 필요는 없습니다. 코드는 아래 아카이브에 첨부되어 있습니다: 알고리즘의 논리에 있는 차이점에 특별한 주의를 기울일 필요가 있습니다. 단계별 형식은 다음과 같습니다:
- 첫 번째 떼를 위한 중심을 만들고 그 주위에 꿀벌을 배치합니다.
- 이후 무리를 위한 중심을 만들고 중심에서 이전 무리까지의 거리가 R*2(반지름 두 개)보다 큰지 확인한 다음 중심 근처에 꿀벌을 배치합니다.
- 각 벌이 다른 무리보다 R(반경)보다 큰 거리만큼 멀리 떨어져 있도록 정찰 벌을 보냅니다.
- 모든 꿀벌의 체력 함수의 값을 구합니다.
- 무리를 정렬합니다.
- 각 벌 떼의 중앙에 벌들을 배치합니다.
- 정지 기준이 충족될 때까지 p. 4부터 반복합니다.
이미 눈치채셨겠지만 검색 전략에는 근본적인 차이가 있습니다. 클래식 버전에서는 각 지역마다 벌의 수가 다를 수 있지만 여기서는 벌 떼의 크기가 항상 동일합니다. 이는 식량 공급원이 고갈되더라도 지역을 계속 탐사할 수 있도록 하기 위한 것으로 초공간에서 표면을 더욱 철저히 탐사할 수 있게 합니다. 테스트를 통해 이러한 접근법의 정당성을 확인할 수 있습니다. 이제 결과가 개선되고 있습니다. 정찰 꿀벌은 지역 근처에서 날지 않고 클래식 버전에서와 같이 지역의 규칙에 따라 자유 공간으로 날아갑니다. 고전적인 버전의 꿀벌에서는 정찰대가 예상대로 행동하지 않습니다. 왜냐하면 이전에 탐험한 지역에 들어갈 수 있다는 사실을 신경 쓰지 않고 완전히 무작위적인 방향으로 흩어져 가기 때문에 가장 기본적인 탐험 방식에 위배되게 움직이기 때문입니다. 배열의 마지막 무리는 정찰 무리입니다. 이 무리의 경우 "다른 사람의 공간에 들어 가지 마십시오"라는 규칙이 적용됩니다. 단 이 규칙이 무리 전체가 아니라 개별 정찰 꿀벌에게 적용됩니다.
다음은 수정된 버전의 결과입니다:
2022.11.21 21:53:25.104 Test_AO_ABCm (EURUSD,M1) 1 Skin's; Func 1000 실행 결과: 14.009060385607679; 함수 10000 실행 결과: 14.060603974847265
2022.11.21 21:53:25.104 Test_AO_ABCm (EURUSD,M1) 점수1: 0.99720; 점수2: 1.00000
2022.11.21 21:53:30.452 Test_AO_ABCm (EURUSD,M1) 20 Skin's; Func 1000 실행 결과: 7.826824877236677; 함수 10000 실행 결과: 8.735832346695558
2022.11.21 21:53:30.452 Test_AO_ABCm (EURUSD,M1) 점수1: 0.66082; 점수2: 0.71028
2022.11.21 21:53:40.060 Test_AO_ABCm (EURUSD,M1) 500 Skin's; Func 1000 실행 결과: 4.645933304640949; 함수 10000 실행 결과: 4.844246724239038
2022.11.21 21:53:40.060 Test_AO_ABCm (EURUSD,M1) 점수1: 0.48774; 점수2: 0.49853
2022.11.21 21:53:40.060 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:53:45.363 Test_AO_ABCm (EURUSD,M1) 1 Forest's; Func 1000 실행 결과: 15.44507700105064; 함수가 10000 실행 결과 15.662273922787355
2022.11.21 21:53:45.363 Test_AO_ABCm (EURUSD,M1) 점수1: 0.96827; 점수2: 0.98188
2022.11.21 21:53:50.697 Test_AO_ABCm (EURUSD,M1) 20 Forest's; Func 1000 실행 결과: 3.6397442648278924; 함수 10000번 실행 결과: 4.759146560755886
2022.11.21 21:53:50.697 Test_AO_ABCm (EURUSD,M1) 점수1: 0.22818; 점수2: 0.29836
2022.11.21 21:54:01.111 Test_AO_ABCm (EURUSD,M1) 500 Forest's; Func 1000 실행 결과: 1.2349621811342104; 함수가 10000번 결과를 실행: 1.4191098624570897
2022.11.21 21:54:01.111 Test_AO_ABCm (EURUSD,M1) 점수1: 0.07742; 점수2: 0.08897
2022.11.21 21:54:01.112 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:54:06.434 Test_AO_ABCm (EURUSD,M1) 1 Megacity's; Func 1000 실행 결과: 12.0; 함수 10000번 실행 결과: 15.0
2022.11.21 21:54:06.434 Test_AO_ABCm (EURUSD,M1) 점수1: 0.80000; 점수2: 1.00000
2022.11.21 21:54:11.768 Test_AO_ABCm (EURUSD,M1) 20 Megacity's; Func 1000 실행 결과: 1.7; 함수 10000번 실행 결과: 2.35
2022.11.21 21:54:11.768 Test_AO_ABCm (EURUSD,M1) 점수1: 0.11333; 점수2: 0.15667
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) 500 Megacity's; Func 1000 실행 결과: 0.572; 함수 10000번 실행 결과: 0.67
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) 점수1: 0.03813; 점수2: 0.04467
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) C_AO_ABCm에 대한 모든 점수: 0.508357869056105
수정된 알고리즘이 두 개의 변수와 두 함수에 대해 성공을 반복하며 100% 수렴하는 것을 볼 수 있습니다. 전체적으로 결과가 개선되었고 최종 점수가 더 높아졌습니다: 0.50836. 안타깝게도 이러한 방식으로는 결과가 크게 개선되지 않습니다. 많은 양의 변수가 있는 함수에 대한 수렴 문제는 알고리즘 구현의 고전적인 버전에 필적합니다.
참고로 수정된 버전에서는 하이브를 다시 초기화해야 하는 버그가 없습니다.
4. 테스트 결과
| AO | 실행 | Skin | Forest | Megacity(개별) | 최종 결과 | ||||||
| 2개 params(1 F) | 40개 params(20F) | 1000 params(500 F) | 2개 params(1 F) | 40개 params(20F) | 1000 params(500 F) | 2개 params(1 F) | 40개 params(20F) | 1000 params(500 F) | |||
| 1000 | 0.99502 | 0.69826 | 0.50498 | 0.99087 | 0.22374 | 0.08408 | 0.78667 | 0.11667 | 0.04224 | 0.54688 | |
| 10,000 | 0.99599 | 0.86403 | 0.58800 | 0.99302 | 0.65571 | 0.17442 | 0.78667 | 0.26133 | 0.08208 | ||
| 1000 | 0.98744 | 0.61852 | 0.49408 | 0.89582 | 0.19645 | 0.14042 | 0.77333 | 0.19000 | 0.14283 | 0.51254 | |
| 10,000 | 0.99977 | 0.69448 | 0.50188 | 0.98181 | 0.24433 | 0.14042 | 0.88000 | 0.20133 | 0.14283 | ||
| 1000 | 0.99720 | 0.66082 | 0.48774 | 0.96827 | 0.22818 | 0.07742 | 0.80000 | 0.11333 | 0.03813 | 0.50836 | |
| 10,000 | 1.00000 | 0.71028 | 0.49853 | 0.98188 | 0.29836 | 0.08897 | 1.00000 | 0.15667 | 0.04467 | ||
| 1000 | 0.99772 | 0.64085 | 0.49029 | 0.94435 | 0.18937 | 0.07526 | 0.69333 | 0.10333 | 0.04120 | 0.49447 | |
| 10,000 | 1.00000 | 0.68769 | 0.49823 | 0.99755 | 0.26279 | 0.08077 | 1.00000 | 0.15400 | 0.04379 | ||
| 1000 | 0.98436 | 0.72243 | 0.65483 | 0.71122 | 0.15603 | 0.08727 | 0.53333 | 0.08000 | 0.04085 | 0.47695 | |
| 10,000 | 0.99836 | 0.72329 | 0.65483 | 0.97615 | 0.19640 | 0.09219 | 0.82667 | 0.10600 | 0.04085 | ||
요약해 보겠습니다. 놀랍게도 벌집 알고리즘은 부드러운 피부와 개별 메가시티의 두 가지 테스트 함수에 대한 5가지 테스트에서 모두 100% 수렴을 보이며 경이로운 속도와 수렴 품질을 보여주었습니다. 그러나 이는 두 개의 변수가 있는 함수에만 적용됩니다. 확장성 측면에서 이 알고리즘은 등급 테이블의 다른 요소들 보다 열등합니다. 여러 변수가 있는 함수는 확실히 꿀벌 군집에 좋지 않습니다. 이는 테스트 스탠드의 애니메이션과 표에 제공된 결과에서 모두 확인할 수 있습니다.
ABC 알고리즘을 사용하려면 사용자가 스웜의 크기, 정찰벌의 수, 지역의 반경 등 여러 매개변수의 설정을 직접 조작해야 합니다. 이러한 설정을 특정 애플리케이션에 맞게 적절하게 선택하지 않으면 알고리즘이 조기에 수렴하거나 전혀 수렴하지 않게 될 수도 있습니다. 또한 ABC는 복잡한 함수에 대한 느린 수렴, 로컬 솔루션 캡처 및 평범한 검색 속성과 같은 단점이 있습니다.
장점:
1. 비교적 빠릅니다.
2. 변수가 적은 부드러운 이산 함수를 위한 놀라운 컨버전스.
단점:
1. 알고리즘의 매개변수들이 결과에 미치는 영향이 큽니다.
2. 범용성이 없습니다.
3. 지역적 극한에 갇힙니다.
4. 평균 확장성.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/11736
 Expert Advisor 개발 기초부터(20부): 새로운 주문 시스템 (III)
Expert Advisor 개발 기초부터(20부): 새로운 주문 시스템 (III)
 Expert Advisor 개발 기초부터(21부): 새로운 주문 시스템(IV)
Expert Advisor 개발 기초부터(21부): 새로운 주문 시스템(IV)
 베어스 파워 보조 지표로 트레이딩 시스템을 설계하는 방법 알아보기
베어스 파워 보조 지표로 트레이딩 시스템을 설계하는 방법 알아보기