모집단 최적화 알고리즘: 개미 군집 최적화(ACO)
모든 행동의 가장 큰 비밀은 사회적 행동입니다...
F. 바틀렛
콘텐츠
1. 소개
2. 알고리즘 원리
3. 수정된 버전
4. 테스트 결과
1. 소개
벨기에의 연구원 마르코 도리고는 개미 군집의 집단 지성 과정을 과학적으로 설명하는 수학적 모델을 만들었습니다. 그는 1992년 박사 학위 논문에서 이를 발표하고 알고리즘으로 구현했습니다. 개미 군집 최적화(ACO)는 여러 넓은 범위의 조합 최적화 문제를 해결하기 위한 인구 기반의 확률적인 검색 방법입니다. ACO는 낙인의 개념을 기반으로 합니다. 1959년 피에르 폴 그라셋은 흰개미의 둥지 짓기 행동을 설명하기 위해 낙인 이론을 발명했습니다. Stigmergy 두 개의 그리스어 단어로 구성되어 있습니다: stigma - 사인, ergon - 행동.
표준적인 정의는 환경과의 상호작용을 통해서 시간이 지남에 따라 일어나는 확장된 집단 구성원 간의 간접적인 유형의 상호작용입니다. 달리 표현하면 에이전트 중 한 명이 흔적을 남기거나 로케일을 어떻게든 수정하여 다른 에이전트가 해당 지역에 진입할 때 정보를 수신하도록 합니다. 개미의 경우 낙인은 페로몬입니다. 낙인의 예로는 개미가 먹이를 찾는 과정에서 서로 간에 간접적으로 의사소통을 하며 땅에 페로몬 흔적을 남기고 이것이 다른 개미의 의사 결정 과정에 영향을 미치는 것을 들 수 있습니다. 개미들 간의 이러한 단순한 형태의 의사소통은 개미집 전체의 복잡한 행동과 능력을 만들어냅니다.
개미는 사회적 곤충이며 군집 생활을 합니다. 개미의 행동은 먹이를 찾는 목적에 따라 제어됩니다. 개미들이 수색하는 동안 개미들은 식민지를 배회합니다. 개미는 먹이를 찾아 한 장소에서 다른 장소로 반복해서 점프하고 이동하면서 페로몬이라는 유기 화합물을 바닥에 쌓아 둡니다. 이렇게 개미는 페로몬 흔적을 사용하여 서로 통신합니다.
개미는 먹이를 발견하면 운반할 수 있는 만큼만 운반합니다. 개미가 집으로 돌아갈 때 먹이의 양과 질에 따라 페로몬을 축적합니다. 결과적으로 다른 개미들도 이 경로를 따라갈 수 있는 것입니다. 페로몬 수치가 높을수록 특정 경로를 선택할 확률이 높아지고 특정 경로를 통과하는 개미가 많을수록 이 경로에 페로몬이 더 많이 남게 됩니다.
다음의 예시를 살펴보겠습니다. 식민지에서 식량을 얻는 방법이 두 가지가 있다고 가정해 보겠습니다. 첫째 지상에 페로몬이 없는 경우입니다. 따라서 이 두 경로를 선택할 확률은 동일합니다(50%). 개미 두 마리가 먹이로 향하는 서로 다른 두 가지 경로를 선택한다고 가정해 보겠습니다. 이 두 경로의 거리는 서로 다릅니다. 더 짧은 경로를 택한 개미가 다른 개미보다 먼저 먹이에 도달합니다. 개미가 먹이를 찾으면 먹이 중 일부를 가져가 식민지로 돌아갑니다. 돌아가는 길에 개미는 페로몬을 바닥에 뿌립니다. 더 짧은 경로를 택한 개미가 더 빨리 식민지에 도착합니다.
세 번째 개미가 먹이를 찾아 나가고 싶을 때 지상의 페로몬의 수준에 따라 거리가 더 짧은 경로를 택합니다. 짧은 경로가 긴 경로보다 페로몬이 더 많기 때문에 세 번째 개미는 페로몬이 더 많은 경로를 따라갑니다. 개미가 더 긴 경로를 따라 식민지로 돌아왔을 때는 이미 더 많은 개미가 페로몬 수치가 높은 경로를 선택한 후였습니다. 이후 다른 개미가 군집에서 목적지(먹이)로 이동하려고 할 때 개미는 각 경로의 페로몬 수치가 동일하다는 것을 알게 됩니다. 그래서 개미는 무작위로 그 중 하나를 선택합니다. 이 과정을 계속해서 반복하면 시간이 지나면 짧은 경로에 다른 경로보다 더 많은 페로몬을 있게 되고 개미들이 이 경로를 택할 확률은 높아집니다.
ACO 알고리즘은 일종의 군집 지능 알고리즘입니다. 개미 군집의 먹이 찾기 과정을 모델링하여 개미 군집의 내부의 데이터 전송 메커니즘을 사용해 다양한 환경에서 최단 경로를 설정합니다. 경로에 남아 있는 페로몬의 농도가 높을수록 개미가 이 경로를 선택할 확률이 높아집니다. 동시에 페로몬의 농도는 시간이 지남에 따라 감소합니다. 따라서 개미 군집의 행동을 통해 개미는 피드백 메커니즘으로 최단 먹이 경로를 결정하기 위해 끊임없이 학습하고 최적화합니다. ACO 알고리즘은 경로 계획에 널리 사용됩니다.
2. 알고리즘 원리
ACO에서는 인공 개미라고 하는 소프트웨어 에이전트 집합이 주어진 최적화 문제에 대한 적절한 솔루션을 찾습니다. 최적화 문제는 ACO를 적용하기 위해 가중 그래프에서 최적의 경로를 찾는 문제로 변환됩니다. 인공 개미들은(이하 개미) 그래프를 따라 점진적으로 솔루션을 구축합니다. 솔루션을 구성하는 과정은 확률론적이고 이를 실행 중에 개미에 의해 값이 변경되는 그래프 구성 요소(노드 또는 에지)와 관련된 매개변수 집합인 페로몬 모델에 따라 달라집니다.
이번에는 여행하는 세일즈맨 문제에 대한 알고리즘을 고려해 보겠습니다. 위치(도시)와 그 사이의 거리가 설정되어 있습니다. 문제는 각 도시를 한 번만 방문하는 최소 길이의 닫힌 경로를 찾는 것입니다. 도시 집합을 그래프의 꼭지점 집합과 연결하여 정의한 그래프를 구성 그래프라고 합니다. 구성 그래프는 특정 도시에서 다른 도시로 이동할 수 있으므로 구성 그래프는 완전히 연결되며 꼭지점의 수는 도시 수와 같습니다. 정점 사이의 에지 길이를 해당 정점이 나타내는 도시 간 거리에 비례하도록 설정하고 페로몬 값과 휴리스틱 값을 그래프 에지와 연결합니다. 페로몬 값은 런타임에 의해 변경되며 개미 군집의 누적적인 경험을 나타내는 반면 휴리스틱 값은 문제에 따라 달라지는 값입니다.
개미는 다음과 같은 방식으로 솔루션을 구성합니다. 각 개미는 무작위로 선택된 도시(구성 그래프 꼭지점)에서 시작합니다. 그런 다음 각 구성 단계에서 그래프의 가장자리를 따라 이동합니다. 각 개미는 경로의 메모리를 저장하고 이후 단계에서 이미 방문한 정점으로 연결되지 않는 가장자리 중에서 선택합니다. 개미는 그래프의 모든 정점을 방문하자마자 솔루션을 구축했습니다. 각 구성 단계에서 개미는 아직 방문하지 않은 정점으로 연결되는 정점 중에서 따라갈 에지를 확률적으로 선택합니다. 확률적 규칙은 페로몬 값과 휴리스틱 정보를 기반으로 하며 에지와 관련된 페로몬과 휴리스틱 값이 높을수록 개미가 특정 에지를 선택할 확률이 높아집니다. 모든 개미가 이동을 완료하면 가장자리에 있는 페로몬이 업데이트됩니다. 각 페로몬 값은 처음에 일정 비율만큼 감소합니다. 이 절차는 종료 기준이 충족될 때까지 반복됩니다.
페로몬 기반의 커뮤니케이션은 자연계에 널리 퍼져 있는 가장 효과적인 커뮤니케이션 방법 중 하나입니다. 페로몬은 꿀벌 개미, 흰개미와 같은 사회성의 곤충이 에이전트 간의 의사소통을 위해 사용하는 물질입니다. 인공 페로몬은 이러한 실현 가능성을 인정 받아 멀티 로봇 및 군집 로봇 시스템을 만드는데 채택되었습니다.
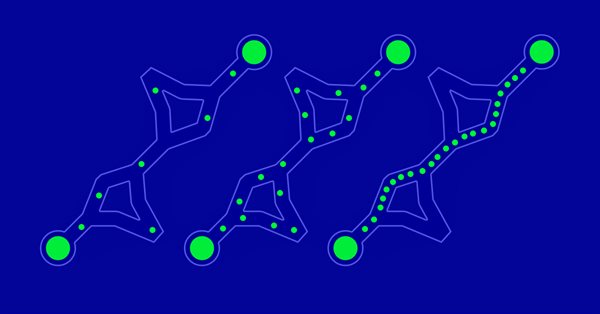
개미가 정말 최단 경로를 찾았다는 것을 어떻게 이해할 수 있을까요? 이에 대한 좋은 테스트 사례가 있습니다: 원 안에 점들이 배열되어 있습니다. 이들에게 최단 경로는 항상 같은 원이 될 것입니다.
최초의 ACO 알고리즘은 개미 시스템이라고 불렸으며 여러 도시를 연결하는 최단 경로를 찾는 것이 목표인 여행하는 세일즈맨의 문제를 해결하기 위한 것이었습니다. 일반적인 알고리즘은 비교적 간단하며 개미 집합을 기반으로 하며 각 개미는 가능한 방문 도시 중 하나를 만듭니다. 각 단계에서 개미는 몇 가지 규칙에 따라 한 도시에서 다른 도시로 이동하는 경로를 선택합니다:
- 개미는 각 도시를 정확히 한 번씩 방문해야 합니다;
- 멀리 떨어진 도시는 선택될 가능성이 낮습니다(가시성);
- 두 도시 사이의 경계에 페로몬 흔적이 더 강렬할수록 이 경계가 선택될 가능성이 높아집니다;
- 경로를 완료한 개미는 경로가 짧으면 통과한 모든 가장자리에 더 많은 페로몬을 축적합니다;
- 이를 반복할 때마다 페로몬 흔적은 증발합니다.

그림 1. 5개의 노드 지점에서 가능한 경로의 예시
3. 수정된 버전
가장 많이 사용되는 ACO 알고리즘의 몇 가지 변형이 알려져 있습니다. 이를 고려해 보겠습니다:
개미 시스템(AS).
개미 시스템은 최초의 ACO 알고리즘입니다.
개미 군집 시스템(ACS).
원래의 개미 시스템은 개미 군집 시스템 알고리즘에서 세 가지 측면에서 수정되었습니다:
1. 에지 선택은 개척에 편향되어 있습니다(페로몬이 더 많은 가장 짧은 에지를 선택할 확률에 유리합니다);
2. 솔루션을 구축할 때 개미는 로컬 페로몬 업데이트 규칙을 적용하여 선택한 가장자리의 페로몬의 레벨을 변경합니다;
3. 각 반복이 끝날 때마다 가장 잘하는 개미만이 수정된 글로벌 페로몬 업데이트 규칙을 적용하여 트랙을 업데이트할 수 있습니다.
엘리트 개미 시스템.
이 알고리즘에서 글로벌 최적 솔루션은 각 반복 후 (흔적을 다시 방문하지 않더라도) 다른 모든 개미와 함께 페로몬을 흔적에 저장합니다. 엘리트 전략의 목표는 모든 개미가 현재의 최적 경로의 링크를 포함하는 솔루션을 구성하도록 모든 개미의 검색을 가르치는 것입니다.
최대-최소 개미 시스템(MMAS).
이 알고리즘은 각 흔적의 최대 및 최소 페로몬의 수를 제어합니다. 최고의 글로벌 투어 또는 최고의 반복 투어만이 자신의 흔적에 페로몬을 추가할 수 있습니다. 검색 알고리즘의 정체를 방지하기 위해 각 추적에서 가능한 페로몬 양의 범위는 [τ max, τ min]의 간격으로 제한됩니다. 모든 에지는 최대 τ로 초기화되어 솔루션의 탐색 속도를 높입니다. 트레이스는 정체에 가까워지면 τ max로 다시 초기화됩니다.
순위에 기반한 개미 시스템(아스랭크).
모든 솔루션은 길이에 따라 순위가 매겨집니다. 이 반복에서 정해진 수의 최고의 개미만이 도전 과제를 업데이트할 수 있습니다. 각 용액에 대해 침착된 페로몬의 양을 측정하여 경로가 짧은 용액이 경로가 긴 용액보다 더 많은 페로몬을 침착 시킵니다.
병렬 개미 군집 최적화(PACO).
커뮤니케이션 전략이 포함된 개미 군집 시스템(ACS).
인공 개미는 여러 그룹으로 나뉩니다. 여행하는 세일즈맨 문제를 해결하는 ACS의 그룹 간에 페로몬 수치를 업데이트하기 위해 7가지 커뮤니케이션 방법이 제안되었습니다.
연속 직교 개미 군집(COAC).
COAC 페로몬 침착 메커니즘을 통해 개미는 협력적이고 효율적으로 해결책을 모색할 수 있습니다. 직교 설계 방법을 사용하면 허용 영역에 있는 개미는 향상된 글로벌 탐색 기능과 정확성을 기반으로 선택한 영역을 빠르고 효율적으로 탐색할 수 있습니다. 직교 설계 방법과 적응 반경 튜닝 방법은 또 다른 최적화 알고리즘으로 확장하여 실제 문제 해결에 더 폭넓은 이점을 제공할 수 있습니다.
개미 군집의 재귀적 최적화.
이것은 전체 검색 영역을 여러 개의 하위 도메인으로 나누고 이러한 하위 도메인에서 문제를 해결하는 재귀적인 형태의 개미 군집입니다. 모든 하위 도메인의 결과를 비교하여 가장 우수한 몇 개의 도메인이 다음 단계로 이동합니다. 선택한 결과에 해당하는 하위 도메인을 더 세분화하여 원하는 정확도를 얻을 때까지 프로세스를 반복합니다. 이 방법은 잘못된 지구 물리학적 반전 문제에 대해 테스트하여 그 효율성을 입증했습니다.
위에서 고려한 개미 군집 알고리즘은 원래는 그래프에서 최적화 문제를 해결하기 위해 개발되었습니다. 문제가 이러한 알고리즘에 통합되고 문제 조건은 그래프 노드의 좌표인 알고리즘 파라미터로 제공됩니다. 따라서 ACO 원칙에 기반한 알고리즘은 고도로 전문화되어 있습니다. 이러한 알고리즘은 고정된 좌표를 사용하지 않기 때문에 우리의 작업에는 적용되지 않습니다. 그러나 유사한 좌표를 포함한 모든 좌표가 있을 수 있습니다. 신경망 트레이닝을 포함한 금융상품 트레이딩 분야의 광범위한 최적화 문제를 해결하려면 새로운 범용 알고리즘을 개발해야 하며 이는 우리의 특별한 테스트를 통과할 수 있는, 즉 완전히 새로운 ACO여야 합니다.
알고리즘의 기본 개념에 대해 생각해 봅시다. 원래의 버전과 마찬가지로 개미 군집이 생깁니다. 우리는 페로몬으로는 이동 경로를 표시할 수 없습니다. 개미들은 다차원 공간의 어느 곳이든 이동하고 경로를 기억하고 저장할 수 있습니다. 연속적인 단계를 사용하면 동일한 경로를 따라갈 확률이 0이 되는 경향이 있기 때문에 적절하지 않은 것 같습니다. 또한 반복없이 순차 통과하는 문제가 없기 때문에 알고리즘에서 노드를 암기 할 필요가 전혀 없습니다. - 이 문제를 알고리즘에서 제거해야 합니다. 그렇다면 어떻게 해야 할까요? 이 단계에서는 개념을 발전시키는 데에 어떤 방향을 취해야 할지 불분명합니다.
그럼 다시 한 번 새로운 알고리즘과 기존 알고리즘을 구별하는 주요 사항에 주목해 보겠습니다:
1. 공간에는 고정된 점이 없습니다.
2. 특정 순서로 경로를 통과할 필요가 없습니다.
3. 경로가 없기 때문에 페로몬으로 표시할 것이 없습니다.
이제 개미 군집에 대해 우리가 염두에 두고 있는 것이 무엇인지 알아봅시다. 개미가 이동한 경로가 아니라 개미가 걸었던 바로 그 지점을 페로몬으로 표시할 수 있습니다. 피트니스 함수의 값을 현재 반복 시 개미의 위치에 있는 페로몬의 수로 설정해 보겠습니다. 그러면 개미는 페로몬이 가장 많이 있는 좌표로 이동해야 합니다. 하지만 모든 개미가 페로몬이 가장 많은 한 지점으로만 달려가면 문제가 발생할 수 있습니다. 포인트가 최적화 함수의 변수라는 점을 고려할 때 이것이 반드시 문제에 대한 최선의 해결책은 아닙니다. 고전적인 ACO에서는 노드에 대한 경로 길이도 중요하다는 것을 기억해야 합니다. 선택한 경로가 짧을수록 좋습니다. 따라서 현재 위치에서 개미가 가야 할 곳까지의 거리를 계산해야 합니다. 우리는 다른 개미들이 있는 곳, 즉 개미들이 어느 정도의 무작위성을 가지고 서로를 향해 이동한다는 개념을 받아들입니다.
움직임에 어떤 종류의 무작위성을 추가할 수 있을까요?
- 먼저 다음 위치 PheromoneEffect_P를 선택할 때 무작위 요소를 추가합니다.
- 둘째, 다음 위치 PathLengthEffect_P까지의 거리를 고려한 무작위 인수를 추가합니다(거리가 작을수록 더 좋은 선택입니다).
따라서 우리에게는 다음의 위치를 선택할 때 개미가 위치한 각 특정 위치의 페로몬 양과 모든 지점 사이의 거리라는 두 가지 기준이 있게 됩니다. 그러나 이 두 가지 선택 기준만 사용하여 이 작업을 수행하더라도 개미는 가상의 도형의 가장자리를 따라 공간에서 이동하며 그 노드는 자신의 위치입니다. 따라서 더 나은 장소를 찾는 과정에 진전이 없을 것입니다.
이 경우 개미가 페로몬을 감지할 수 있는 페로몬의 영향 반경인 PheromoneRadius_P (점 사이의 거리 비율)를 추가합니다. 그러면 개미는 이동한 지점을 지나갈 수 있습니다. 이렇게 하면 개미들이 다차원 공간에서 이동할 때 추가적인 자유도를 부여할 수 있습니다.
개미들이 새로운 영역을 탐색하도록 하려면 개미들을 좌표를 따라 방향 벡터에서 벗어날 수 있도록 허용해야 합니다. 특정 좌표에서 증분과의 편차를 제공하는 PathDeviation_P 비율을 소개해 보겠습니다. 다차원 공간에서는 변위 벡터에 따라 일부 좌표는 양의 증분을 가질 수 있고 다른 좌표는 음의 증분을 가질 수 있으며 증분은 서로 다른 모듈로 값을 가질 수 있습니다. 이 비율은 이 모든 것을 고려할 수 있게 해주며 개미가 먹이를 찾을 때 어느 정도의 자유(기능의 극한)를 줄 것입니다.
그렇다면 변위 벡터는 무엇이며 개미가 이동해야 하는 거리를 어떻게 측정할 수 있을까요? 이러한 질문에 답하려면 3차원 공간에서 두 점 사이의 거리를 계산하는 방정식을 사용하세요:
![]()
그림 2를 보면 변위 벡터의 시각적 표현을 얻을 수 있습니다.
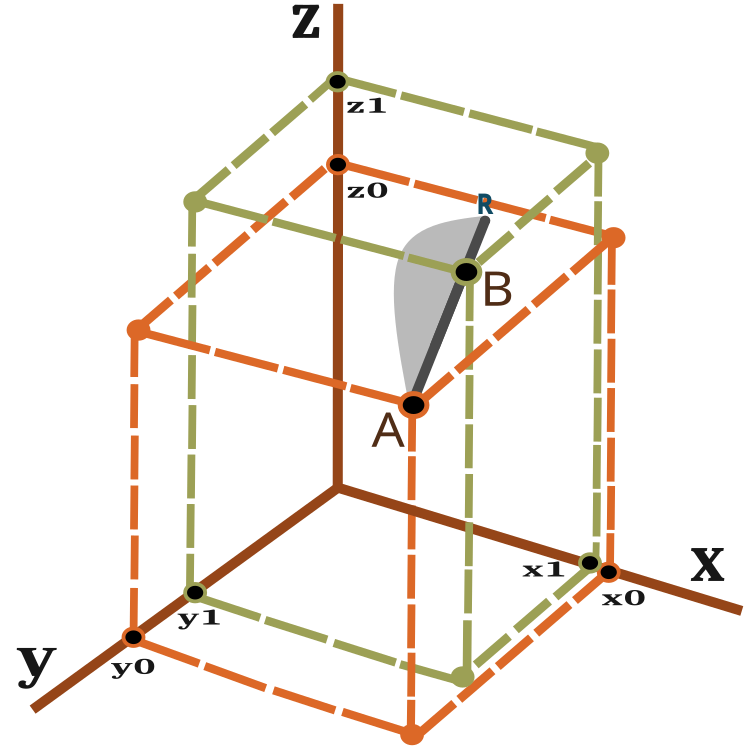
그림 2. 개미 이동 벡터
n차원 공간의 경우 계산 방식도 비슷합니다.
한 반복(에포크)에 있는 개미는 점 A에서 점 B로 이동하면서 점 R로 미끄러질 수 있습니다. 점 B에서 점 R까지의 거리는 PheromoneRadius_P 비율에 따라 달라지며 BR = AB x PheromoneRadius_P로 계산할 수 있습니다.
AR 라인에서 새로운 위치의 확률은 그림 2에 회색 영역으로 개략적으로 표시되어 있습니다(축척 없음). 따라서 개미의 새로운 위치는 B 지점으로 향할 가능성이 더 높습니다. 확률 이동의 원리는 이전 글에서 설명한 바 있습니다.
알고리즘에는 각 반복마다 다음과 같은 단계가 포함됩니다:
1) 공간에 개미를 무작위로 배열합니다.
2) 개미의 페로몬 양(피트니스 함수)의 값을 결정합니다.
3) 한 개미에서 다른 개미까지의 거리를 계산합니다.
4) 개미가 이동할 선호 지점을 선택합니다.
5) AR 벡터에서 점의 확률 계산.
6) AR 벡터에서 얻은 점의 좌표를 계산합니다.
7) 정지 조건이 충족될 때까지 2단계부터 반복합니다.
그럼 이제 알고리즘 코드에 대한 설명을 이어가겠습니다. 먼저 개미에 대한 설명이 포함된 구조를 작성해 보겠습니다:
- c [] - 개미 좌표,
- cLast [] - 이전 좌표입니다,
- cB [] - 모든 반복에 대한 최적의 좌표입니다,
- F - 현재 페로몬 값입니다,
- fB - 모든 반복에서 도달한 최대 페로몬 값입니다.
개미 구조의 생성자에서는f와 fB의 값을 'double' 유형으로 표현할 수 있는 최소값으로 초기화합니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Ants { double cLast []; //last coordinates double c []; //coordinates double cB []; //best coordinates double f; //pheromone of the current coordinates double fB; //pheromone of the best coordinates S_Ants () { f = -DBL_MAX; fB = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
모든 개미 사이의 쌍별 거리를 저장할 수 있는 배열이 있는 구조가 필요합니다.
struct S_Paths { double a []; };
이전 기사에서 살펴본 최적화 알고리즘을 구성하는 발전된 개념의 프레임 워크 내에서 필요한 세 가지 공개 메서드만 있는 클래스로 수정 된 ACO 알고리즘을 작성하겠습니다 - InitAnts (), Preparation ( ) 및 Dwelling (). 또한 이미 알고리즘의 표준이 된 다른 비공개 메서드 뿐만 아니라 GenerateRNDants( ) 및 AntsMovement() 비공개 메서드도 있습니다. ants [] 구조 배열은 개미들의 군집입니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACO { public: //---------------------------------------------------------------------------- S_Ants ants []; //ants double rangeMax []; //maximum search range double rangeMin []; //manimum search range double rangeStep []; //step search double cB []; //best coordinates double fB; //pheromone of the best coordinates void InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP); void Preparation (); void Dwelling (); private: //---------------------------------------------------------------------------- S_Paths paths []; int coordinates; //number of coordinates int antHillSize; //ant hill size double goals []; double pheromoneEffect; double pathLengthEffect; double pheromoneRadius; double pathDeviation; bool dwelling; void GenerateRNDants (); void AntsMovement (); double SeInDiSp (double in, double inMin, double inMax, double step); double RNDfromCI (double min, double max); double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
초기화 메서드에서 변수와 배열 크기에 초기 값을 할당합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP) { fB = -DBL_MAX; coordinates = coordinatesP; antHillSize = antHillSizeP; pheromoneEffect = pheromoneEffectP; pathLengthEffect = pathLengthEffectP; pheromoneRadius = pheromoneRadiusP; pathDeviation = pathDeviationP; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); dwelling = false; ArrayResize (ants, antHillSize); ArrayResize (paths, antHillSize); for (int i = 0; i < antHillSize; i++) { ArrayResize (ants [i].c, coordinates); ArrayResize (ants [i].cLast, coordinates); ArrayResize (ants [i].cB, coordinates); ArrayResize (paths [i].a, antHillSize); } ArrayResize (cB, coordinates); ArrayResize (goals, antHillSize); } //——————————————————————————————————————————————————————————————————————————————
각각의 반복에서 Preparation ( ) 메서드가 먼저 호출됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Preparation () { if (!dwelling) { fB = -DBL_MAX; GenerateRNDants (); dwelling = true; } else AntsMovement (); } //——————————————————————————————————————————————————————————————————————————————
GenerateRNDants () 메서드는 무작위의 개미 군집을 생성하는 역할을 합니다. 개미 좌표는 주어진 한도 내에서 무작위로 할당됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::GenerateRNDants () { for (int s = 0; s < antHillSize; s++) { for (int k = 0; k < coordinates; k++) { ants [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); ants [s].c [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); ants [s].cLast [k] = ants [s].c [k]; ants [s].cB [k] = ants [s].c [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Dwelling () 메서드에서 개미의 현재 좌표를 기억하고 현재 반복 시점에 얻은 최대 페로몬의 값을 업데이트합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Dwelling () { for (int i = 0; i < antHillSize; i++) { ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY); //remember the best coordinates for the ant if (ants [i].f > ants [i].fB) { ants [i].fB = ants [i].f; ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY); } //remember the best coordinates for the anthill if (ants [i].f > fB) { fB = ants [i].f; ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
AntsMovement () 알고리즘의 주요 메서드입니다. 이 메서드는 한 개미에서 다른 개미까지의 거리 계산, 개미가 이동할 선호 지점 선택 계산, AR 벡터에서 점의 확률 계산 등의 작업을 수행합니다. AR 벡터에서 얻은 점의 좌표를 계산합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::AntsMovement () { double rndPh; double rndPt; double summCoordinates = 0.0; double scores []; ArrayResize (scores, antHillSize); double maxPh = -DBL_MAX; double minPh = DBL_MAX; double maxPt = -DBL_MAX; double minPt = DBL_MAX; double goal; double goalBest = -DBL_MAX; int goalInd = 0; //measure the distance between all the ants----------------------------------- for (int i = 0; i < antHillSize; i++) { for (int k = 0; k < antHillSize; k++) { if (i == k) { paths [i].a [k] = DBL_MAX; continue; } for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0); paths [i].a [k] = pow (summCoordinates, 0.5); if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k]; if (minPt > paths [i].a [k]) minPt = paths [i].a [k]; } } //---------------------------------------------------------------------------- for (int i = 0; i < antHillSize; i++) { maxPh = -DBL_MAX; minPh = DBL_MAX; for (int k = 0; k < antHillSize; k++) { if (i != k) { if (maxPh < ants [k].f) maxPh = ants [k].f; if (minPh > ants [k].f) minPh = ants [k].f; } } goalBest = -DBL_MAX; goalInd = 0; for (int k = 0; k < antHillSize; k++) { if (i != k) { rndPh = RNDfromCI (0.0, pheromoneEffect); rndPt = RNDfromCI (0.0, pathLengthEffect); goal = Scale (ants [k].f, minPh, maxPh, 0.0, 1.0, false) * rndPh * Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true) * rndPt; if (goalBest < goal) { goalBest = goal; goalInd = k; } } } double wayToGoal = paths [i].a [goalInd]; double radiusNearGoal = wayToGoal * pheromoneRadius; double endWay = wayToGoal + radiusNearGoal; double x = RNDfromCI (-1.0, 1.0); double y = x * x; if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay, false); else y = Scale (y, 0.0, 1.0, 0.0, wayToGoal, true); for (int j = 0; j < coordinates; j++) { double incrementFactor = y / wayToGoal; double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j]; ants [i].c [j] = ants [i].cLast [j] + (coordDistance * incrementFactor); double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation; ants [i].c [j] += w; ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
한 숫자 범위에서 다른 숫자 범위로 숫자를 스케일링 하는 함수에 주목해야 합니다. 제가 이전 기사에서 이미 고려한 사항입니다. 이번에는 저는 그 기능을 확장할 것입니다. rever입력은 아래 그림과 같이 배율의 방향을 변경하는 데 사용됩니다.
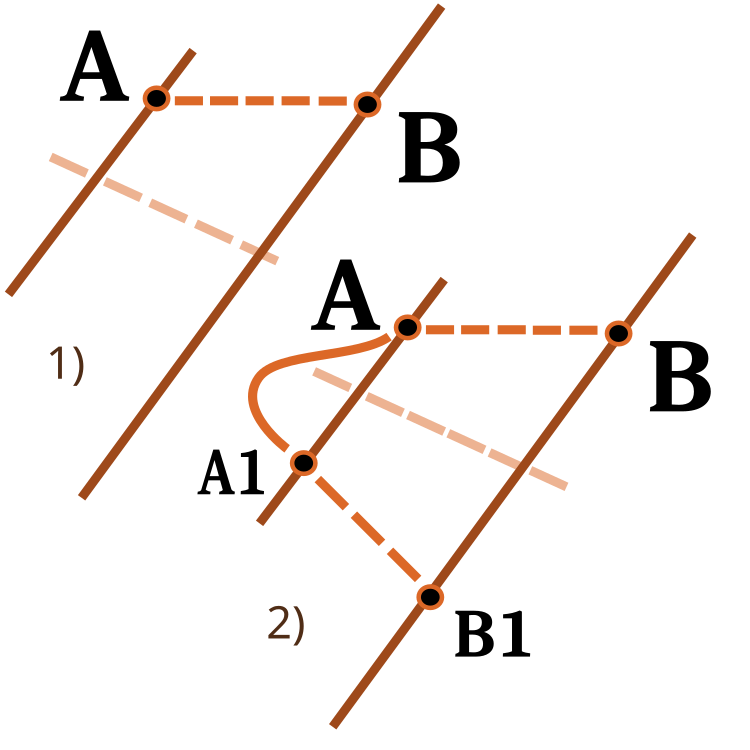
그림 3. 한 숫자 범위에서 다른 숫자 범위로 숫자 배율을 조정합니다.
1) 다이렉트 스케일링, 2) 리버스 스케일링
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return revers ? OutMAX : OutMIN; if (In > InMAX) return revers ? OutMIN : OutMAX; double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); if (!revers) return res; else return OutMAX - res; } } //——————————————————————————————————————————————————————————————————————————————
4. 테스트 결과
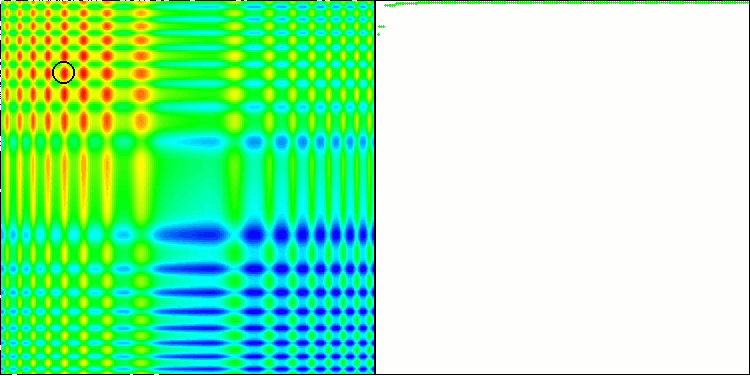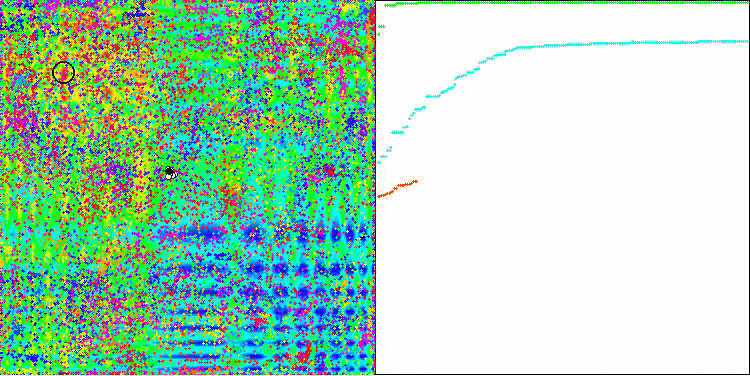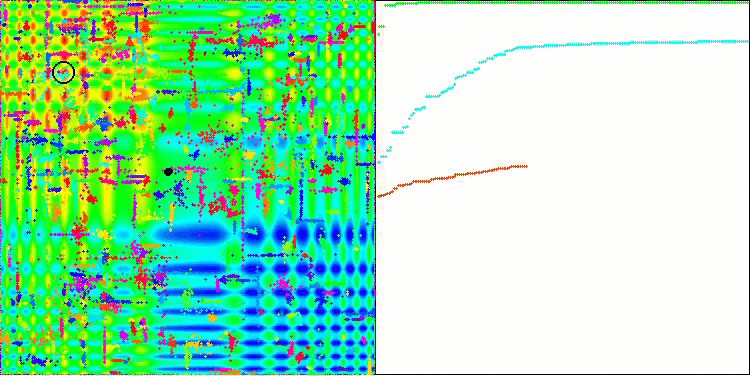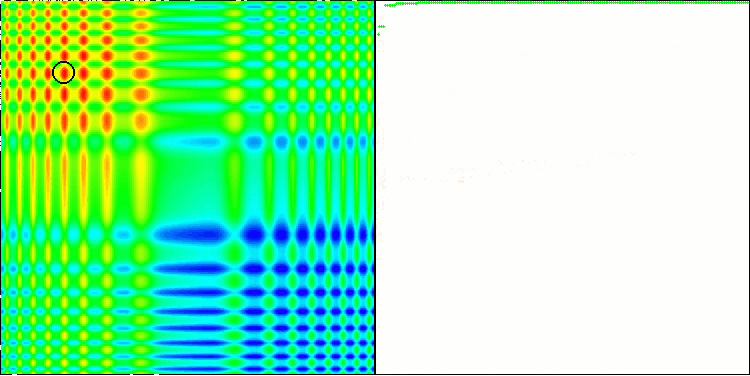
Skin 테스트 함수의 ACO.
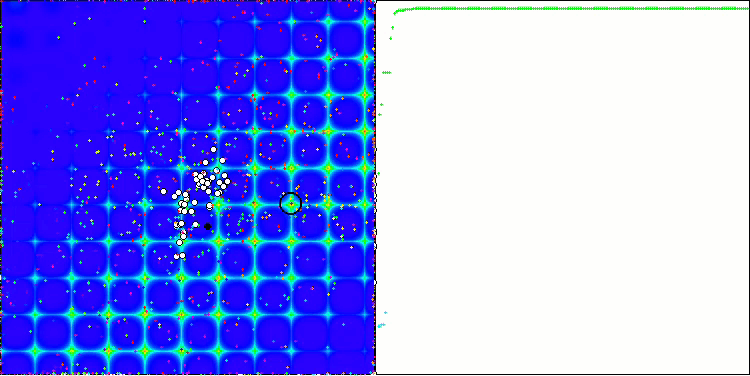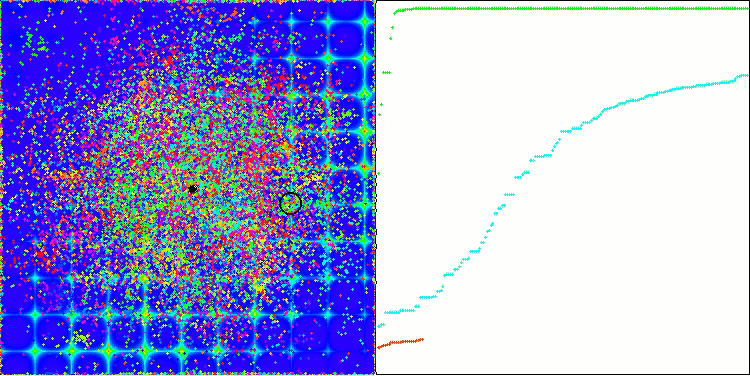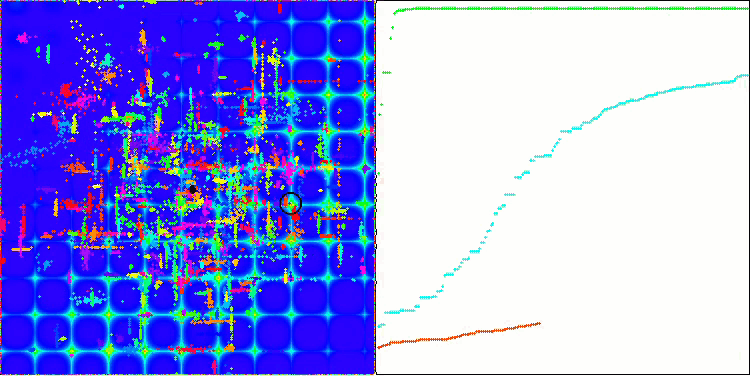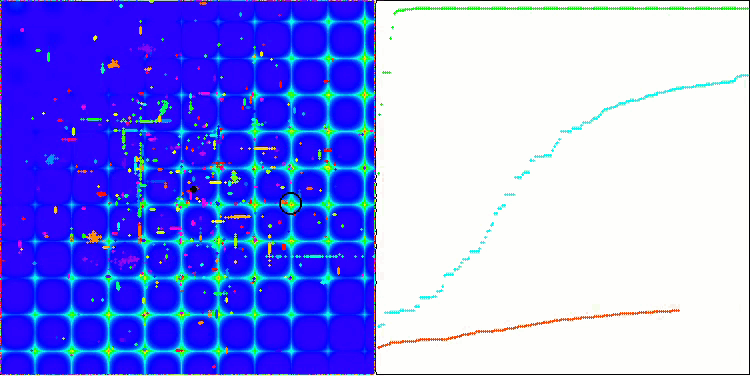
Forest 테스트 함수의 PSO.
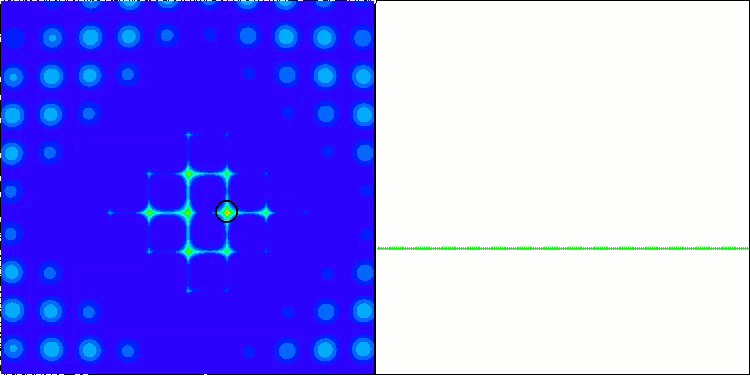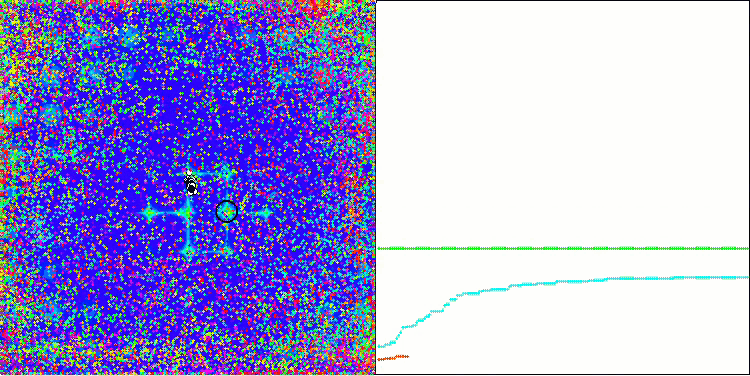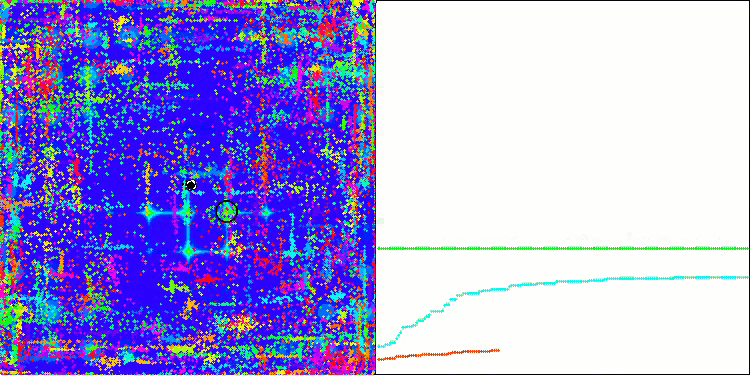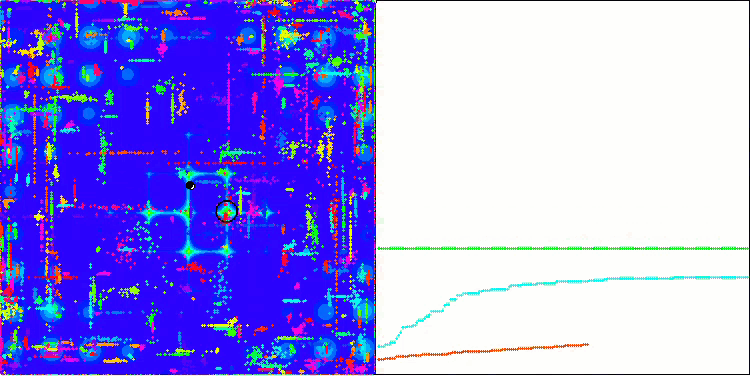
Megacity 테스트 함수의 ACO.
이제 결론을 내릴 시간입니다. 한편으로 전통적인 개미 군집 알고리즘은 금융상품 거래의 최적화 문제에는 적용되지 않습니다. 그러나 기존 버전의 한계를 넘기 위해 완전히 새로운 개념의 개미 군집 알고리즘이 등장하여 ACO를 더욱 발전시킬 수 있게 되었습니다. 이러한 알고리즘은 여행하는 세일즈맨 문제를 비롯한 다양한 문제에 적용될 수 있습니다.
또한 이제 평점표의 새로운 리더가 생겼습니다. 결과를 좀 더 자세히 살펴봅시다. 먼저 테스트 스탠드의 결과에 주의를 기울이세요:
2022.10.27 16:46:28.678 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) 1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) Score1: 0.99502; Score2: 0.99599 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) 20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) Score1: 0.69826; Score2: 0.86403 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) 500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) Score1: 0.50498; Score2: 0.58800 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) 1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) Score1: 0.99087; Score2: 0.99302 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) 20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) Score1: 0.22374; Score2: 0.65571 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) 500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) Score1: 0.08408; Score2: 0.17442 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) 1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) Score1: 0.78667; Score2: 0.78667 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) 20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) Score1: 0.11667; Score2: 0.26133 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) 500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) Score1: 0.04224; Score2: 0.08208 2022.10.27 16:49:41.075 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) All score for C_AO_ACO: 0.5468768583006471
이 알고리즘은 매끄러운 피부 함수에서 우수한 성능을 보였으며 특히 20 및 500 함수 테스트에서 뛰어난 수렴과 우수한 확장 기능을 보여주었습니다. 날카로운 경계선이 있는 부드러운 포레스트 함수에서는 분리가 더욱 두드러집니다. 알고리즘은 로컬 극한값에 도달하더라도 검색을 계속합니다. 이산 메가시티 함수에서 이 알고리즘은 500 함수가 있는 문제에서만 무작위 RND 알고리즘을 산출하였습니다.
| AO | 실행 | 피부 | 포리스트 | 메가시티(개별) | 최종 결과 | ||||||
| 2 params(1 F) | 40 params(20F) | 1000 params(500 F) | 2 params(1 F) | 40 params(20F) | 1000 params(500 F) | 2 params(1 F) | 40 params(20F) | 1000 params(500 F) | |||
| 1000 | 0.99502 | 0.69826 | 0.50498 | 0.99087 | 0.22374 | 0.08408 | 0.78667 | 0.11667 | 0.04224 | 0.54688 | |
| 10,000 | 0.99599 | 0.86403 | 0.58800 | 0.99302 | 0.65571 | 0.17442 | 0.78667 | 0.26133 | 0.08208 | ||
| 1000 | 0.98744 | 0.61852 | 0.49408 | 0.89582 | 0.19645 | 0.14042 | 0.77333 | 0.19000 | 0.14283 | 0.51254 | |
| 10,000 | 0.99977 | 0.69448 | 0.50188 | 0.98181 | 0.24433 | 0.14042 | 0.88000 | 0.20133 | 0.14283 | ||
| 1000 | 0.98436 | 0.72243 | 0.65483 | 0.71122 | 0.15603 | 0.08727 | 0.53333 | 0.08000 | 0.04085 | 0.47695 | |
| 10,000 | 0.99836 | 0.72329 | 0.65483 | 0.97615 | 0.19640 | 0.09219 | 0.82667 | 0.10600 | 0.04085 | ||
| 1000 | 0.96678 | 0.64727 | 0.57654 | 0.80616 | 0.13388 | 0.06800 | 0.53333 | 0.08067 | 0.04211 | 0.45144 | |
| 10,000 | 0.99505 | 0.64986 | 0.57654 | 0.90401 | 0.18194 | 0.07104 | 0.74667 | 0.10400 | 0.04211 | ||
결론
알고리즘에는 많은 설정이 가능합니다. 그러므로 우리는 더 나은 결과를 얻을 수 있습니다. 우리는 특정 유형의 작업에 맞도록 자유롭게 설정할 수 있습니다. 첫 번째 매개변수인 PheromoneEffect_P는 수렴 속도에 직접적인 영향을 줍니다. 이 매개변수는 포물선과 같은 부드럽고 단조로운 함수에 특히 유용합니다. 수렴은 100%가 되지만 동시에 크게 설정하면 이산 함수의 국부적인 극한에 갇히게 되는 원인이 되기도 합니다.
두 번째 매개변수 PathLengthEffect_P는 개미의 게으름의 정도를 나타냅니다. 매개변수 값이 높으면 더 가까운 타겟이 이동 대상으로 선택됩니다. 최상의 결과를 얻으려면 이 매개변수와 첫 번째 매개변수 사이의 균형을 맞출 필요가 있습니다. 이 매개 변수는 개미가 더 많은 먹이가 있는 지점으로 이동하려는 욕구에 균형추를 제공하도록 설계되었습니다. 대신에 작은 영역을 더 자세히 조사하기 위해 가장 가까운 대상을 선택하는 경우가 있는데 이는 포리스트 함수의 예에서와 같이 가장 좋은 지점이 매우 가까운 것으로 판명될 수 있는 경우에 매우 유용할 수 있습니다.
가장 중요한 성과는 이산 조합 문제만 해결할 수 있다는 기존 ACO의 주요 문제점을 제거했다는 점입니다. 이제 개미 군집 알고리즘을 사용하여 신경망을 훈련할 수 있을 것입니다.
시각적으로 테스트 스탠드는 특정 클러스터링으로 인해 관찰하기에 매우 흥미롭습니다. 개미는 다차원 함수의 측정에 집중되어 특정한 방식으로 국부적인 극단의 특징적인 그룹을 강조합니다. 아마도 이 효과는 특정한 문제를 해결하는 데 사용될 수 있을 것이지만 추가적인 연구가 필요할 것입니다.
이 알고리즘에는 흥미로운 속성이 있습니다. 40개의 변수를 최적화할 때보다 두 개의 변수가 있는 문제를 해결할 때 국부 극한에 갇힐 확률이 다소 높다는 것입니다. 알고리즘은 여러 변수가 포함된 솔루션을 계속 검색합니다. 저는 이것이 검색 공간의 모든 좌표를 연결하는 수단으로 벡터를 사용한 결과라고 가정합니다. 예를 들어 개미가 더 나은 새로운 장소로 이동했다면 좌표 중 일부가 개별적으로 변경되는 것이 아니라 모든 좌표가 공간적으로 더 나은 방향으로 변경된 것입니다.
생성된 알고리즘은 새로운 것이고 자세히 검증되지 않았으므로 제가 표의 결과를 업데이트 할 수 있도록 테스트 스탠드가 0.6보다 큰 최종 값을 표시하는 알고리즘의 설정을 공유해 주시면 감사하겠습니다. 저의 요청은 이전에 살펴본 알고리즘에 적용됩니다.
1. 알고리즘이 매우 빠릅니다.
2. 다용도성. 이 알고리즘은 다양한 최적화 문제에 사용할 수 있습니다.
3. 로컬 극한에만 집중하지 않는 기능.
4. 매끄러운 함수와 불연속 함수 모두에 대해 상당히 우수한 컨버전스를 제공합니다.
5. 확장성.
단점:
1. 아마도 원활한 기능을 위해서는 동일한 PSO보다 수렴에 더 많은 반복이 필요하지만 PSO가 이미 중지된 경우에도 검색을 계속할 수 있는 기능을 통해 부분적으로 상쇄됩니다.
2. 알고리즘 매개변수가 결과에 미치는 영향이 큽니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/11602
 베어스 파워 보조 지표로 트레이딩 시스템을 설계하는 방법 알아보기
베어스 파워 보조 지표로 트레이딩 시스템을 설계하는 방법 알아보기
 Expert Advisor 개발 기초부터(20부): 새로운 주문 시스템 (III)
Expert Advisor 개발 기초부터(20부): 새로운 주문 시스템 (III)
 포스 인덱스 지표로 트레이딩 시스템을 설계하는 방법 알아보기
포스 인덱스 지표로 트레이딩 시스템을 설계하는 방법 알아보기