
모집단 최적화 알고리즘: 뻐꾸기 최적화 알고리즘(COA)
콘텐츠
1. 소개2. 알고리즘 설명, 의사 결정 트리 및 레비 비행
3. COA 코드
4. 테스트 결과
1. 소개
뻐꾸기는 노래뿐만 아니라 다른 새의 둥지에 알을 낳는 공격적인 번식 전략을 가진 매혹적인 새입니다. 따라서 이 새는 부모의 책임을 다른 종으로 완전히 옮깁니다. 뻐꾸기는 각 종마다 특정한 색깔과 크기의 알을 낳아 다양한 양부모의 알과 가장 잘 어울리도록 합니다. 다른 새의 둥지에 던져진 뻐꾸기 새끼는 보통 둥지 주인의 새끼보다 크고 힘이 세기 때문에 뻐꾸기에게는 더 많은 먹이가 필요합니다. 호지슨의 뻐꾸기 새끼는 성장하는 동안 날개에 부리가 열린 형태의 특별한 무늬가 생겨 양부모로부터 더 많은 먹이를 받을 수 있습니다. 뻐꾸기만이 이러한 특성을 보이는 새는 아닙니다. 이렇게 둥지에 기생하는 방식은 최소 80종의 조류에서 발견되었습니다. 이러한 현상은 암컷이 다른 식민지로 침투하여 여왕을 죽이고 알을 낳는 호박벌, 꿀벌 및 개미와 같은 일부 사회적 곤충 종에서 널리 퍼져 있습니다. 아프리카 탕가니카 호수의 메기처럼 알을 품고 있는 다른 물고기에게 알을 던져주는 일부 물고기들 사이에도 둥지 기생이 존재합니다.
뻐꾸기 검색은 양과 뎁이 2009년에 개발한 알고리즘으로 자연에서 영감을 얻은 최신 휴리스틱 알고리즘 중 하나입니다. 이 알고리즘은 일부 뻐꾸기 종의 기생을 기반으로 합니다. 이 알고리즘은 단순한 등방성 랜덤 워크 방식이 아닌 소위 레비 비행으로 더욱 개선되었습니다.
2. 알고리즘 설명
뻐꾸기 최적화 알고리즘(COA)은 지속적인 비선형 최적화에 사용됩니다. COA는 이 새의 생활 방식에서 영감을 받았습니다. 최적화 알고리즘은 이러한 종의 알을 낳고 번식하는 특징을 기반으로 합니다. 다른 진화적 접근 방식과 마찬가지로 COA는 초기 모집단에서 시작합니다. 이 알고리즘의 기본 원리는 생존을 위한 시도입니다. 생존을 위해 경쟁하는 동안 일부 새들은 죽습니다. 살아남은 뻐꾸기는 더 좋은 장소로 이동하여 번식하고 알을 낳기 시작합니다. 마지막으로 살아남은 뻐꾸기들은 비슷한 체력 값을 가진 뻐꾸기들이 사회를 이루는 방식으로 수렴합니다.
이 방법의 가장 큰 장점은 단순성입니다: 뻐꾸기 검색에는 누구나 이해할 수 있는 네 가지 매개 변수만 필요하므로 튜닝이 쉬워집니다.
뻐꾸기 검색 알고리즘에서 둥지 안의 알은 최적화 문제에 대한 해결책으로 간주되며 뻐꾸기의 알은 새로운 해결책을 나타냅니다. 이 알고리즘의 궁극적인 목표는 현재의 둥지 알을 대체하기 위해 이 새로운(그리고 잠재적으로 더 나은) 기생하는 뻐꾸기 알을 사용하는 것입니다. 반복적으로 수행되는 이러한 교체는 결국 솔루션으로 이어집니다.
양 교수와 뎁 교수는 알고리즘에 대해 다음과 같은 세 가지의 이상적인 상태 세트를 제안했습니다:
1. 뻐꾸기는 알을 하나씩 낳고 무작위로 선택된 둥지에 떨어뜨립니다.
2. 고품질의 알을 품은 최고의 둥지는 다음 세대에 물려줄 것입니다.
3. 사용 가능한 둥지의 수는 고정되어 있으며 둥지는 'p' 확률로 다른 종류의 알을 감지할 수 있습니다. 이 경우 숙주인 새가 알을 버리거나 둥지를 떠나면 알은 죽게 됩니다.
간단하게 하기 위해 세 번째 가정은 n개의 둥지의 pa 분율로 근사화할 수 있습니다. 최대화 문제의 경우 솔루션의 품질 또는 적절성은 단순히 목적 함수에 비례할 수 있습니다. 그러나 피트니스 함수에 대한 다른 (더 복잡한) 표현식도 정의될 수 있습니다.
g의 각 반복 마다 뻐꾸기 알 i가 무작위로 선택되고 일정한 확률 분포를 갖는 스텝 길이의 범위 내에서 스텝이 결정되며 스텝의 방향이 등방성이고 무작위인 일종의 무작위 보행인 레비 비행을 사용하여 새로운 해 xi(g + 1)를 생성합니다. 이러한 방법을 처음 만든 사람들에 따르면 레비 비행을 사용하는 전략은 다른 단순한 무작위 보행보다 전반적인 성능이 더 좋기 때문에 선호한다고 합니다. 일반적인 레비 비행 방정식은 다음과 같습니다.
xi(g + 1) = xi(g) + α ⊕ levy(λ),
여기서 g는 현재 세대의 수를 나타내고 α > 0은 연구 중인 특정 문제의 규모와 관련이 있어야 하는 스텝의 크기를 나타냅니다. ⊕ 기호는 요소별 곱셈을 나타내는 데 사용됩니다. g + 1 세대 다음의 위치는 g 세대의 현재 위치와 첫 번째 및 두 번째 항에 의해 각각 주어진 전이 확률에만 의존하기 때문에 본질적으로 마르코프 체인입니다. 이 전환 확률은 다음과 같이 레비 분포에 의해 변조됩니다:
levy(λ) ∼ g-λ, (1 < λ ≤ 3)
는 무한한 평균과 무한한 분산을 갖습니다. 연습을 실행한 결과 2.0으로 고정할 때 가장 좋은 결과를 얻을 수 있는 것으로 나타났습니다. 여기서 스텝은 기본적으로 파워로프 헤비테일 스텝 길이 분포를 가진 무작위 보행 프로세스를 형성합니다. 계산적 관점에서 보면 레비 비행을 사용한 난수의 생성은 두 단계로 구성됩니다. 먼저 균일한 분포에 따라 임의의 방향을 선택한 다음 선택한 레비 분포에 따라 단계를 생성합니다. 그런 다음 알고리즘이 새로운 솔루션의 적합성을 평가하고 현재 솔루션과 비교합니다. 새로운 솔루션이 더 적합한 경우 현재의 솔루션을 대체합니다. 반면에 더 좋고 솔루션을 찾기 위해 그리고 검색 공간의 탐색을 늘리기 위해 일부의 둥지는 버려집니다(둥지의 주인이 뻐꾸기 알을 버리거나 둥지를 떠나 알이 죽게 내버려둠). 교체율은 성능을 개선하기 위해 조정해야 하는 모델 매개변수인 PA 확률에 의해 결정됩니다. 알고리즘은 중지 기준이 충족될 때까지 반복적으로 적용됩니다. 일반적인 종료 기준은 더 낮은 임계값을 만족하는 솔루션을 찾았거나 고정된 세대 수에 도달했거나 연속적인 반복을 통해 더 이상 더 나은 결과를 얻지 못하는 경우입니다.
뻐꾸기가 알을 낳는 과정에 대해 더 자세히 살펴 보겠습니다. 모든 둥지 중에서 알을 낳을 둥지가 무작위로 선택됩니다. 알은 솔루션이기 때문에 알의 품질로 표현될 수 있습니다. 뻐꾸기 알의 품질이 부모의 알보다 높으면 뻐꾸기 알은 교체됩니다. 그렇지 않으면 부모의 알이 둥지에 남아있게 됩니다. 실제로는 살아남은 병아리로부터 이어지는 진화가 계속됩니다. 즉 부모 알의 새끼가 살아남았다면 같은 곳에서 진화가 계속된다는 뜻입니다. 추가 개발은 뻐꾸기 알이 더 살아갈 수 있는 것으로 판명되고 문제 해결을 위한 검색이 새로운 장소에서 계속되는 경우에만 가능합니다. 의사 결정 트리는 그림 1에 개략적으로 나와 있습니다.
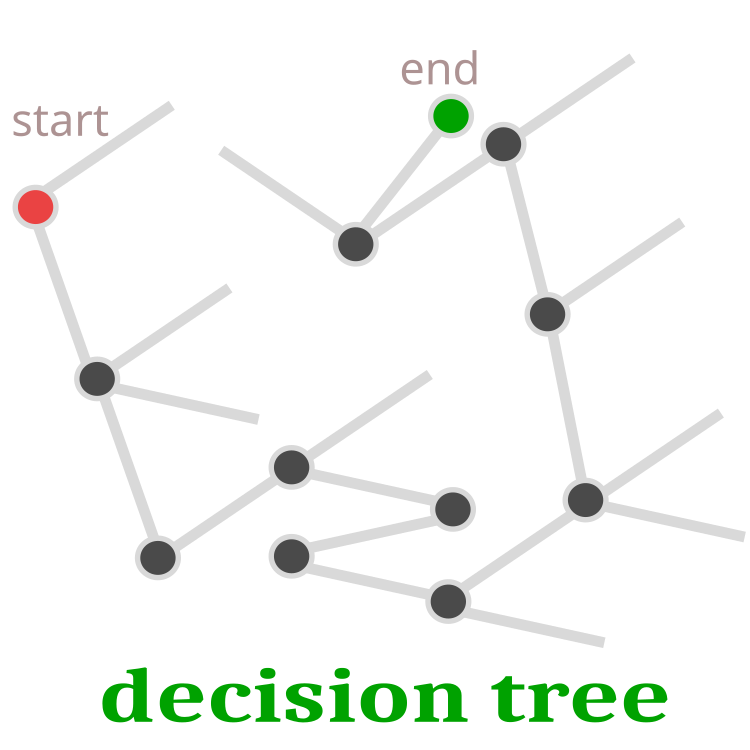
그림 1. 의사 결정 트리. 빨간색 점이 시작이고 녹색 점이 최종 결정입니다.
의사 결정 트리 후 알고리즘의 기초를 이루는 두 번째 구성 요소는 레비 비행입니다. 레비 비행은 점프의 길이가 단계별로 바뀌고 점프의 방향이 무작위로 바뀌며 확률 분포가 파레토 분포의 특수한 경우로 무거운 꼬리가 특징인 랜덤 보행(마르코프 통계 과정)입니다. 레비 비행은 공간에서의 점프로 정의되며 점프는 임의의 방향으로 등방성입니다. 레비 비행은 변칙적인 확률적 프로세스를 설명하는 도구입니다. 분산은 무한하며(긴 길이의 점프가 가능) 점프 길이는 모든 레벨에서 자체적으로 유사합니다(짧은 점프와 긴 비행이 산재되어 있음). 레비 비행이라는 용어는 때때로 연속적인 공간이 아닌 불연속적인 그리드에서 발생하는 랜덤 워크를 포함하는 것으로 확장 되기도 합니다.
하나의 매개변수를 가진 최적화 문제를 풀기 위해 레비 비행 뻐꾸기 알고리즘의 적용을 생각해 볼 수 있습니다. 정의 영역의 대부분, 즉 수평선(y=x)에 걸쳐 변하지 않는 가상의 함수(그림 2의 검은색 선)를 예로 들어 보겠습니다. 작은 영역에서만 함수가 변경되며 최대 한 번만 변경됩니다. 그림 2의 주황색 점으로부터 최대값 검색을 시작한 이후 레비 분포로 임의의 값 x를 구하면 함수에서 아무런 변화는 얻지 못하면서 시작점에서 멀어지게 됩니다. 그러나 분포의 꼬리가 강하게 점프하면 원래의 주황색보다 더 좋은 솔루션인 녹색 점이 나타나고 우리는 녹색 점에서만 결과를 개선할 수 있습니다 동시에 함수의 최대값에 접근하면서 말입니다. 이 예에서 레비 비행은 알고리즘의 검색 기능을 획기적으로 개선합니다.
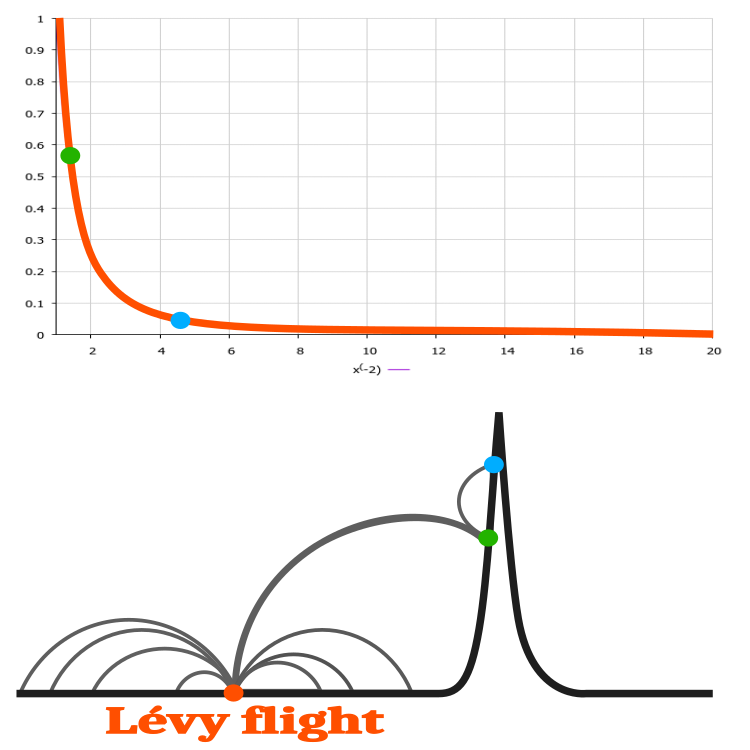
그림 2. 레비 비행을 사용하여 가상의 1차원 함수에 대한 해를 구하는 예제.
레비 비행의 개념은 카오스 이론에서 무작위 또는 유사 무작위 자연 현상(예: 긴 궤적과 짧은 궤적을 결합한 알바트로스의 비행)을 모델링할 때 사용됩니다. 예로는 지진 데이터 분석, 금융 수학, 암호화, 신호 분석, 난류 운동은 물론 천문학, 생물학, 물리학의 다양한 응용 분야가 있습니다.
COA 알고리즘 의사 코드(그림 3):
1. 임의의 값을 가진 뻐꾸기 초기화.
2. 피트니스 정의.
3. 무작위 둥지에 알 낳기.
4. 주어진 확률로 둥지를 비우기.
5. 현재 위치에서 레비 비행 거리 내의 임의의 방향으로 뻐꾸기를 보내기.
6. 피트니스 정의.
7. 무작위 둥지에 알 낳기.
8. 주어진 확률로 둥지를 비우기.
9. 정지 기준이 충족될 때까지 p.5를 반복.
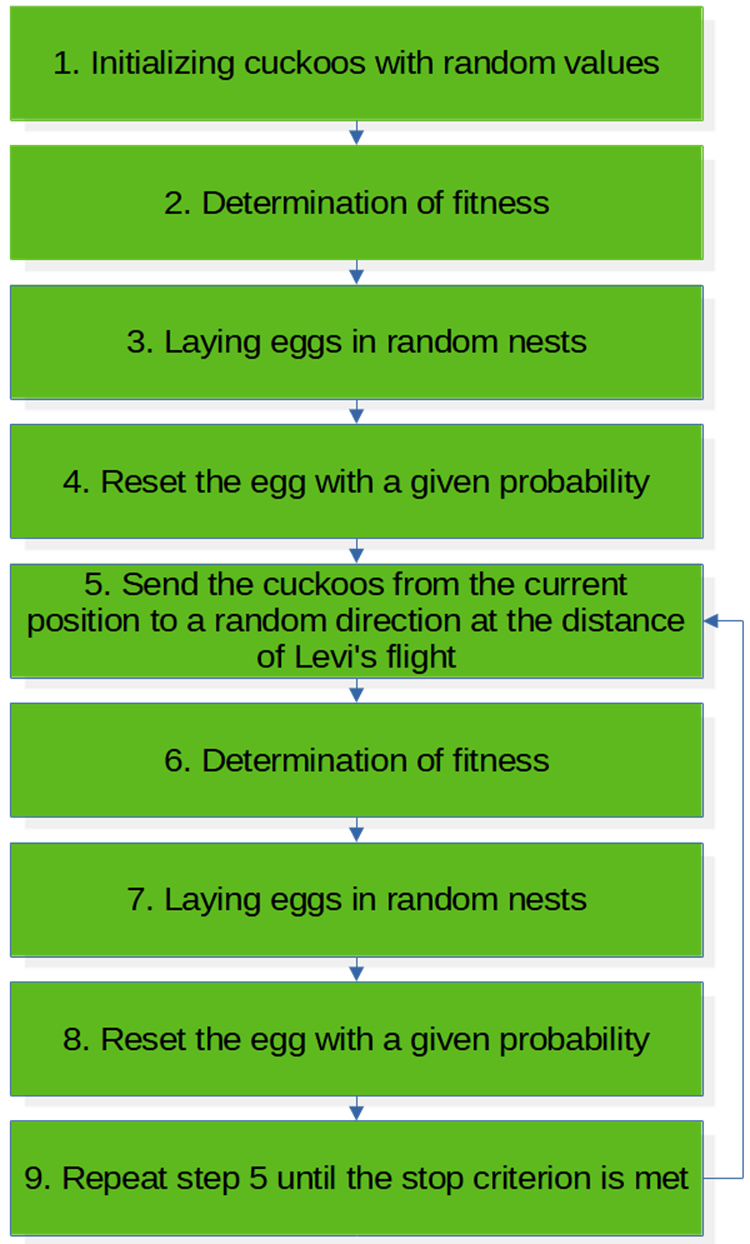
그림 3. COA 알고리즘 블록 다이어그램
3. COA 코드
알고리즘의 코드를 살펴봅시다. 문제에 대한 해결책은 뻐꾸기, 즉 알입니다. 이것은 검색 공간의 좌표와 적합도 함수(알 품질)의 값을 포함하는 간단한 구조입니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Cuckoo { double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
둥지를 구조물의 형태로 설명해 보겠습니다. 여기에는 달걀의 구조에서와 마찬가지로 공간의 좌표와 피트니스 함수의 값이 있습니다. "둥지에 알을 낳는다"는 것은 본질적으로는 알의 구조를 둥지의 구조에 복사하는 것을 의미합니다. pa 확률 매개변수를 사용하는 경우, 0.0에서 pa까지의 난수가 [0.0;1.0] 범위에서 떨어지고 e의 값이 -DBL_MAX로 설정되면 알이 둥지에서 방출됩니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Nest { void Init (int coordinates) { ArrayResize (c, coordinates); e = -DBL_MAX; } double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
알고리즘 클래스. 퍼블릭 초기화 메서드, 사용자 프로그램에서 호출하는 주요 두 가지 메서드, 최적화 문제의 인수 값 범위 및 서비스 기능을 수행하는 추가 프라이빗 메서드가 여기에 선언됩니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Cuckoo cuckoos []; //all the cuckoos public: double cB []; //best coordinates (egg parameters) public: double eB; //best eggs quality public: void Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP); //step control value public: void CuckooFlight (); public: void LayEggs (); //============================================================================ private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: S_Nest nests []; //nests private: int cuckoosNumber; //number of cuckoos private: int nestsNumber; //number of cuckoo nests private: double koef_pa; //probability of detection of cuckoo eggs private: double koef_alpha; //step control value private: double v []; private: int coordinates; //coordinates number private: bool clutchEggs; //clutch of eggs }; //——————————————————————————————————————————————————————————————————————————————
Init () 퍼블릭 메서드. 여기서 변수 값이 재설정되고 배열에 메모리가 할당됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP) //step control value { MathSrand (GetTickCount ()); clutchEggs = false; eB = -DBL_MAX; coordinates = coordinatesP; cuckoosNumber = cuckoosP; nestsNumber = nestsP; koef_pa = koef_paP; koef_alpha = koef_alphaP; ArrayResize (nests, nestsNumber); for (int i = 0; i < nestsNumber; i++) { nests [i].Init (coordinates); } ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (v, coordinates); ArrayResize (cuckoos, cuckoosNumber); for (int i = 0; i < cuckoosNumber; i++) { ArrayResize (cuckoos [i].c, coordinates); } } //——————————————————————————————————————————————————————————————————————————————
첫 번째 공개 메서드는 "뻐꾸기 비행"의 각 반복에서 호출됩니다. clutchEggs 플래그가 꺼져 있으면 뻐꾸기를 임의의 방향으로 보내서 해당 좌표 범위의 난수를 생성합니다. 플래그가 활성화된 경우 뻐꾸기의 실제 비행은 v 벡터 범위에서 레비 비행의 분포에 따라 수행됩니다. 좌표마다 값의 범위가 다를 수 있으므로 각 좌표에 대해 Init ()에서 v 벡터를 개별적으로 미리 계산합니다.
뻐꾸기 [i].c [c] = 뻐꾸기 [i].c [c] + r1 * v [c] * pow (r2, -2.0); 식은 오프셋 r1 * v [c] * pow (r2, -2.0)을 더한다는 의미이며 여기서 r1은 -1 또는 1로 원래 위치에서 오프셋의 방향을 결정하고 v는 변위 벡터이고 r2는 0.0에서 20.0 범위의 난수를 제곱 -2.0으로 제곱한 값입니다. 임의의 숫자를 제곱으로 올리는 것이 레비 비행 함수입니다. 그래프는 그림 2에서 확인할 수 있습니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::CuckooFlight () { //---------------------------------------------------------------------------- if (!clutchEggs) { for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } clutchEggs = true; } else { double r1 = 0.0; double r2 = 0.0; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; r2 = RNDfromCI (1.0, 20.0); cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
각 반복에서 호출되는 두 번째 퍼블릭 메서드는 "알 낳기"입니다. 이 메서드에서는 뻐꾸기 알을 둥지에 낳는 시뮬레이션을 알고리즘으로 재현합니다. 이는 기존의 모든 둥지 중에서 무작위로 둥지를 선택하는 방식으로 이루어집니다. 그 후 뻐꾸기 알의 품질과 이미 둥지에 있는 뻐꾸기 알의 품질을 비교합니다. 뻐꾸기 알이 더 좋으면 교체가 이루어집니다. 이 메서드에서 알고리즘의 특징은 뻐꾸기 알이 더 적합하더라도 알이 죽을지 여부에 대한 확률이 산란 후에 수행된다는 것입니다. 즉 자연에서와 마찬가지로 어떤 알이 무엇이든 죽게 될 koef_pa가능성이 있습니다. 알이 죽거나 둥지에서 버려진 경우 이는 실제로는 같은 일이며 둥지는 모든 종류의 체력을 가진 알을 새로 낳을 수 있도록 자유로울 것이며 이는 알고리즘적으로 새로운 장소에서의 연구를 의미합니다.
이렇게 하면 둥지 기생과 같은 자연 진화의 방법 중 하나를 단 몇 줄의 코드로 설명할 수 있습니다. 많은 책의 저자들은 새로운 무작위 값으로 알을 제거한 후 둥지를 초기화할 것을 권장하는데 이는 처음부터 검색을 시작하는 것을 의미합니다. 대부분의 경우 이러한 방법은 알고리즘의 탐색 능력을 향상시키는 측면에서 원하는 결과를 얻지 못합니다. 저의 연구에 따르면 알의 품질에 관계없이 둥지를 비워 두면 뻐꾸기 중 하나가 그 안에 알을 낳는 것이 지름길이라는 것을 보여주었습니다. 이는 무작위 값보다 낫습니다. 연구의 변동성은 현재 좌표에서 임의의 방향으로 무작위로 점프하여 제공됩니다. 결과적으로 최적의 솔루션을 찾기 위한 반복 횟수가 줄어들어 전체적으로는 알고리즘의 수렴 속도가 빨라집니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::LayEggs () { int ind = 0; //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ for (int i = 0; i < cuckoosNumber; i++) { ind = (int)round (RNDfromCI (0.0, nestsNumber - 1)); if (cuckoos [i].e > nests [ind].e) { nests [ind].e = cuckoos [i].e; ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY); if (cuckoos [i].e > eB) { eB = cuckoos [i].e; ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY); } } else { ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY); } } //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv for (int n = 0; n < nestsNumber; n++) { if (RNDfromCI (0.0, 1.0) < koef_pa) { nests [ind].e = -DBL_MAX; } } } //——————————————————————————————————————————————————————————————————————————————
4. 테스트 결과
테스트 결과는 다음과 같습니다:
2022.11.30 11:31:54.490 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.918379100238852
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) 점수: 1.00000
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 4.257477577760983
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) 점수: 0.84220
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.3521208312080903
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) 점수: 0.14849
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.7600394018343262
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) 점수: 0.99557
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.4968964923017033
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) 점수: 0.28107
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.07638950254648778
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) 점수: 0.04321
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 12.0
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) 점수: 1.00000
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 2.69
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) 점수: 0.22417
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.40800000000000003
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) 점수: 0.03400
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) C_AO_COA의 모든 점수: 0.507633670637353
레비 비행 뻐꾸기 검색 알고리즘은 인상적인 결과를 보여주었습니다. 대부분의 테스트에서 다른 최적화 알고리즘보다 우수한 성능을 보였습니다. 특히 이 알고리즘은 두 개의 변수가 있는 부드러운 피부 함수와 두 개의 변수가 있는 불연속적인 메가시티 함수에서 100% 수렴을 보였습니다. 더욱 놀라운 점은 이산 함수에서 뛰어난 확장성을 보여주었다는 것입니다. 다른 테스트에서는 개미 군집 알고리즘보다 약간 열등했습니다. 현재 평가표에는 의심할 여지 없는 리더가 있습니다.
모든 알고리즘에는 최종 결과에 어느 정도 영향을 미치는 조정 매개 변수가 있으므로 이러한 알고리즘 중 일부는 더 많은 최적의 매개 변수를 가질 수 있으며 등급 표가 다르게 보일 수 있다는 사실을 명확히 하고 싶습니다. 저는 최상의 결과를 보장하기 위해 제가 찾을 수 있는 매개변수를 사용하여 테스트 결과를 보여드렸습니다. 더 많은 최적의 매개변수를 찾아 더 나은 결과를 얻으면 이를 기반으로 등급표를 수정할 수 있습니다. 개미 알고리즘은 일부 지표에서 뻐꾸기 검색 알고리즘보다 앞서고 최종 지표 측면에서는 살짝 뒤쳐져 있기 때문에 현재 리더와 성공적으로 경쟁 할 수 있다는 가정이 있습니다. GWO는 여전히 1000개의 변수를 가진 스킨 함수의 선두주자입니다. 어쨌든 최적화 문제를 해결할 때 프로젝트에서 알고리즘을 사용하려는 사람들은 표를 탐색하고 특정의 요구에 맞는 알고리즘을 선택할 수 있습니다.
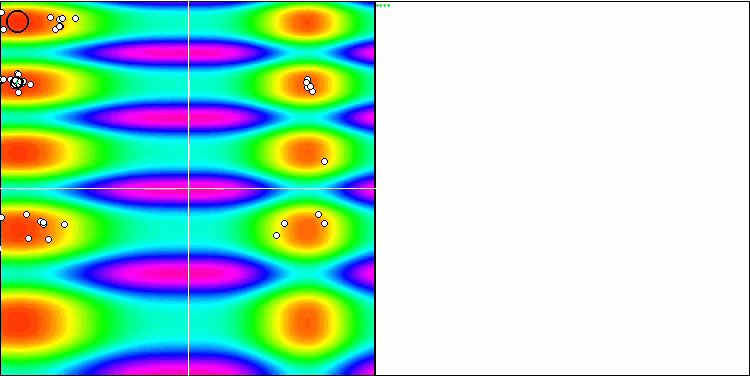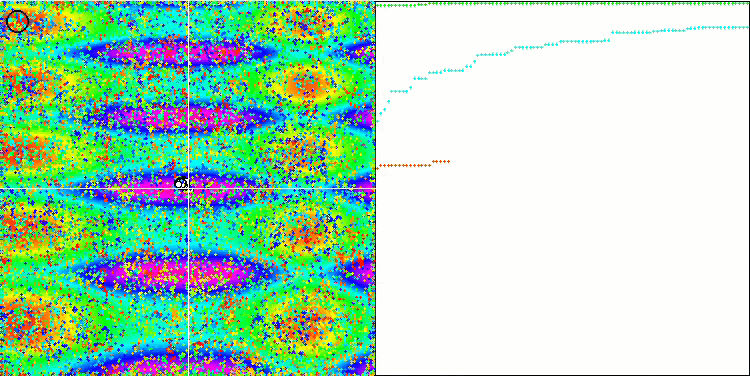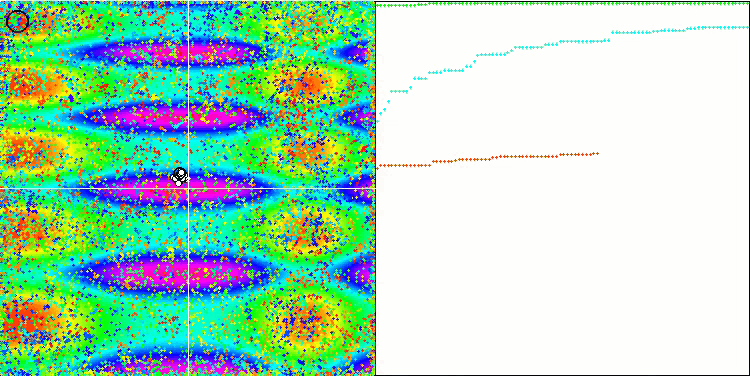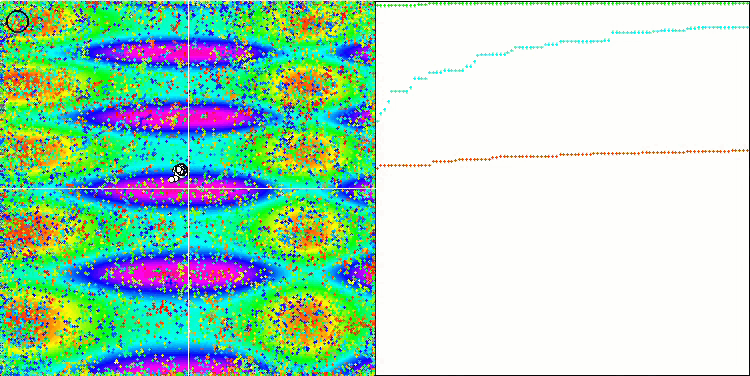
피부 테스트 함수에서 COA.
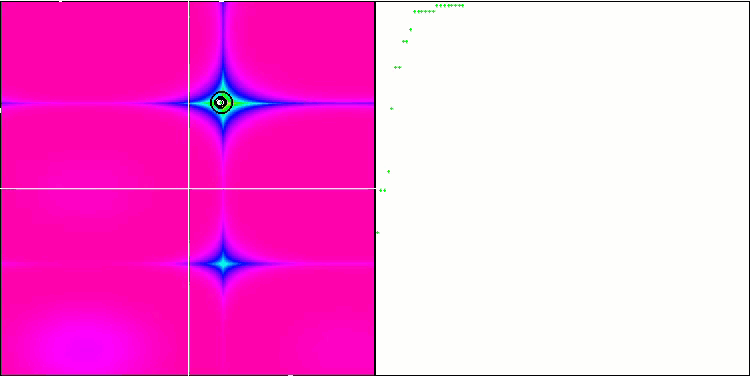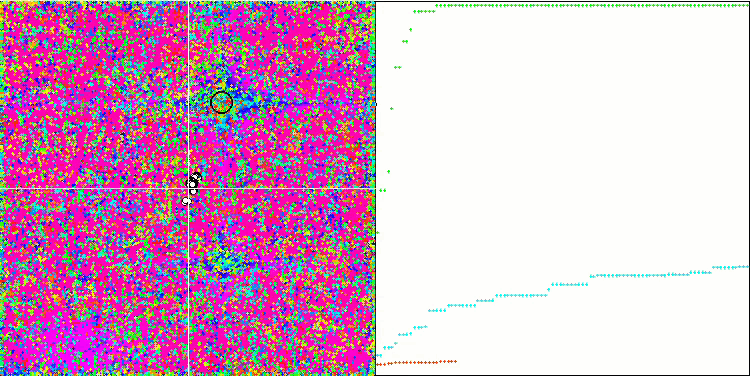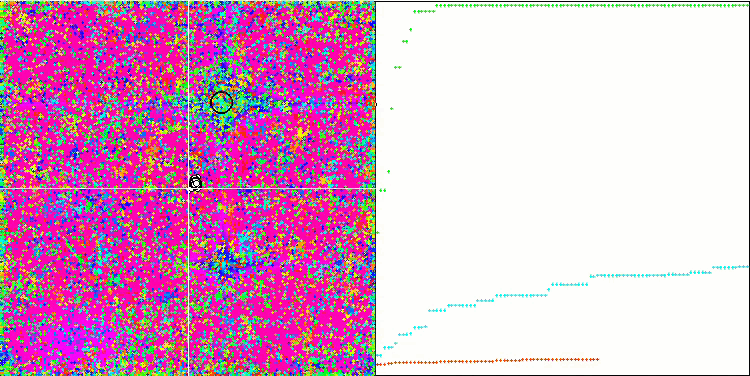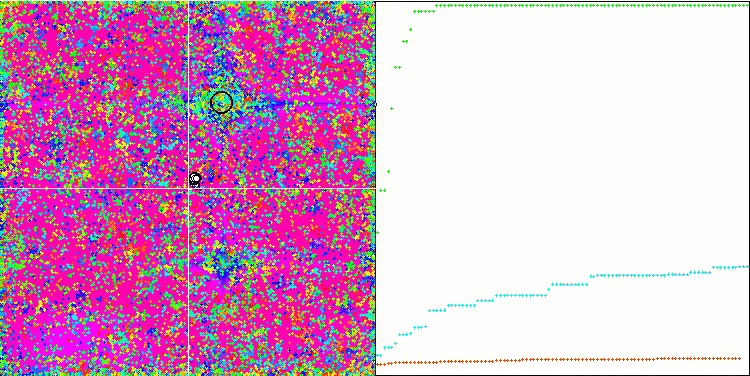
Forest 테스트 함수에서 COA.
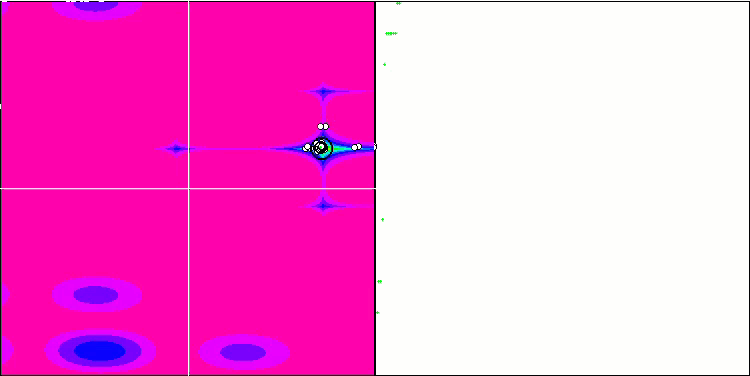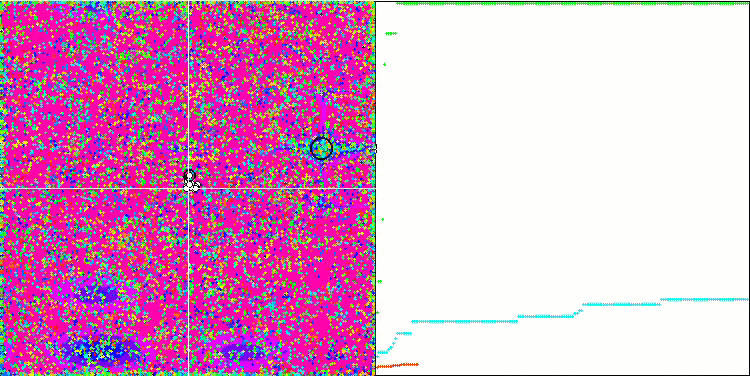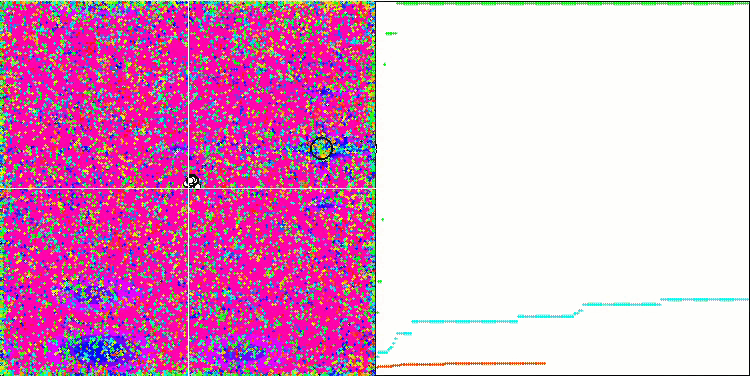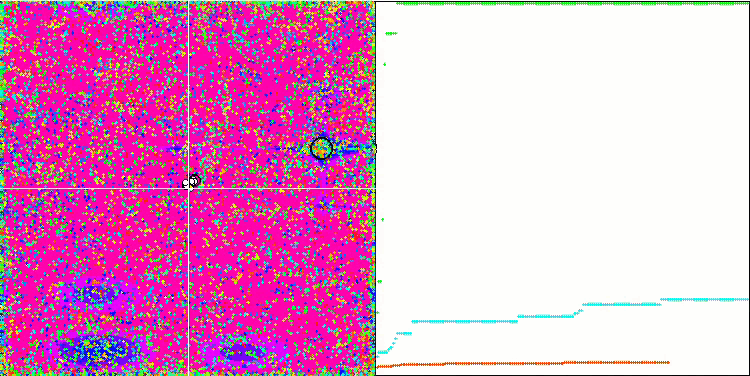
메가시티 테스트 함수에서 COA.
테스트 스탠드의 시각화에서 알고리즘의 동작은 앞서 고려한 것과 다르지만 꿀벌 군집 알고리즘과 같이 작업을 연구 영역으로 나누는 알고리즘의 특징적인 몇 가지 기능이 있습니다. 이는 알고리즘이 하나의 극단에 집중하지 않고 잠재적으로 유망한 여러 영역을 탐색하여 알고리즘이 국부적인 극단에 갇히지 않도록 저항력을 제공한다는 특징이 있습니다. 이와 관련하여 둥지를 정렬하고 뻐꾸기가 품질에 비례하여 둥지를 선택함으로써 알고리즘을 개선할 수 있습니다. 이는 뻐꾸기가 알고리즘의 표준 버전에서처럼 무작위로 선택된 둥지에 알을 넣는 대신 둥지를 선택하는 것을 의미합니다. 그러나 무작위 둥지 선택의 실용성을 입증하는 결과는 개선되지 않았습니다. 아마도 이것은 자연에서 일어나는 일을 반영하는 것일지도 모릅니다. 더 똑똑한 호스트의 경우 알을 교체하는 것은 더 어렵고 무작위로도 통계적으로도 정당화되지 않습니다.
알고리즘의 또 다른 특징은 변수가 많은 함수에서 무작위 보행처럼 작동한다는 점입니다. 시각적으로는 백색 소음이나 오래된 TV 화면처럼 보입니다. 로컬 극한 위치에서 몇몇 좌표의 집중은 반복이 끝날 때까지만 눈에 띄게 나타납니다. 저는 개미 군집 알고리즘의 경우처럼 매개 변수를 더 명확하게 "결정화"하고 싶었습니다. 따라서 우리는 모든 최적화 알고리즘의 일반적인 문제에 도달했습니다. 일반적인 해결책이 없다는 것입니다. 고전적인 알고리즘은 물론 새로운 알고리즘을 다루는 많은 저자들이 이 문제를 해결하려고 시도했습니다.
문제의 본질은 다음과 같습니다: 연구중인 함수의 최적화 된 매개 변수 중 어떤 것이 우선 순위나 강점을 갖는지 확실하지 않으며 각 매개 변수가 결과에 어느 정도 영향을 미치는지 알 수 없습니다. 예를 들어 여러 매개 변수가 있고 알고리즘이 이미 올바른 매개 변수를 찾았지만 정확히 어떤 매개 변수를 찾았는지는 알 수 없습니다. 알고리즘은 계속해서 모든 것을 변경하려고 시도하지만 글로벌 극단에 도달하기 위해서는 일부만 변경하는 것으로 충분합니다. 수만, 수천 개의 변수가 있는 함수의 경우에는 문제가 더욱 심각해 집니다. 변수가 많아질 수록 문제는 더 심각해 집니다. 시각적으로 이것은 화면에서 백색 노이즈처럼 보입니다.
저는 이 문제를 부분적으로나마 해결하려고 시도해 보았습니다. 연구 중인 함수의 매개변수 중 어떤 것을 변경하고 어떤 것을 그대로 유지해야 하는지 선험적으로 알 수 없는 경우에 우리는 확률적인 방법으로 이를 해결할 수 있습니다. 우리는 모든 매개변수를 동시에 변경하는 것이 아니라 일부만 변경해야 한다고 가정합니다. PSO 알고리즘은 특징적인 방식으로 작동합니다. 최적화 함수의 매개 변수(인수) 수가 증가하면 최적화 함수는 집중하는 능력이 없는 구름처럼 작동합니다. 이를 위해 저는 좌표가 변경될 확률을 설정하고 그렇지 않으면 좌표가 동일하게 유지되는 새로운 매개 변수를 알고리즘에 도입했습니다.
그리고 그 결과는... 긍정적이었습니다!!! 테스트 결과가 개선되었습니다. 제가 달성하고 싶었던 '결정화'는 변수가 많은 함수에서 나타났습니다.
테스트 스탠드 결과는 다음과 같습니다:
2022.12.03 16:01:26.256 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) 1 Skin's; Func 10000 실행 결과: 4.918367945334852
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) 점수: 1.00000
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) 20 Skin's; Func 10000 실행 결과: 4.328327964103814
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) 점수: 0.85911
2022.12.03 16:01:59:306 Test_AO_COAm (EURUSD,M1) 500 Skin's; Func 10000 실행 결과: 1.3297901702583084
2022.12.03 16:01:59:306 Test_AO_COAm (EURUSD,M1) 점수: 0.14316
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) 1 Forest's; Func 10000 실행 결과: 1.755200932219688
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) 점수: 0.99283
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) 20 Forest's; Func 10000 실행 결과: 0.5089243656052672
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) 점수: 0.28787
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.08044934398920801
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) 점수: 0.04551
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) 1 Megacity's; Func 10000 실행 결과: 12.0
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) 점수: 1.00000
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) 20 Megacity's; Func 10000 실행 결과: 2.9899999999999998
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) 점수: 0.24917
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.4244
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) 점수: 0.03537
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) C_AO_COAm에 대한 모든 점수: 0.5125572342985216
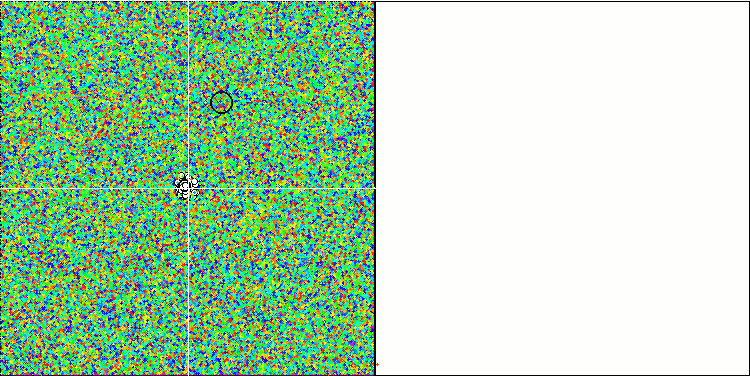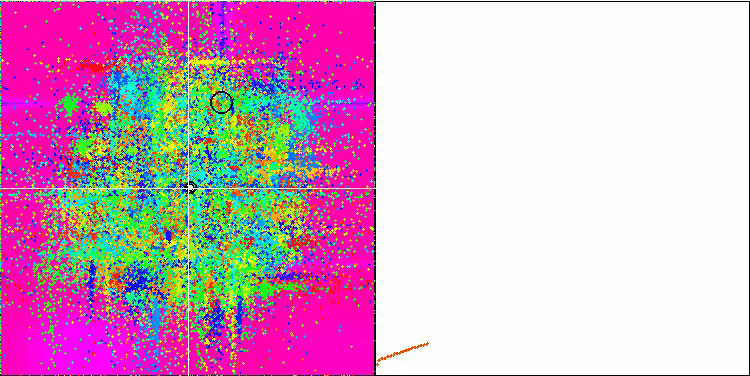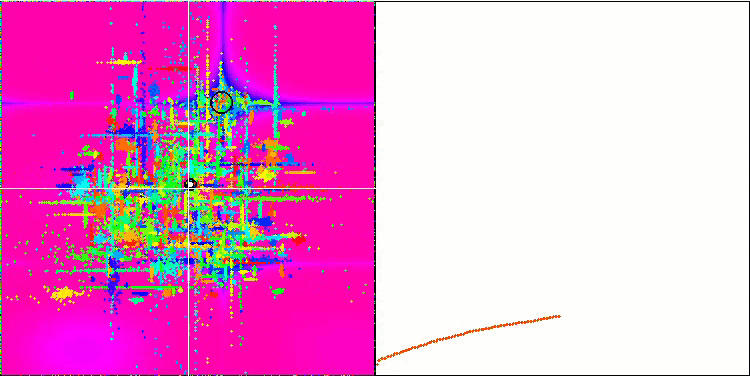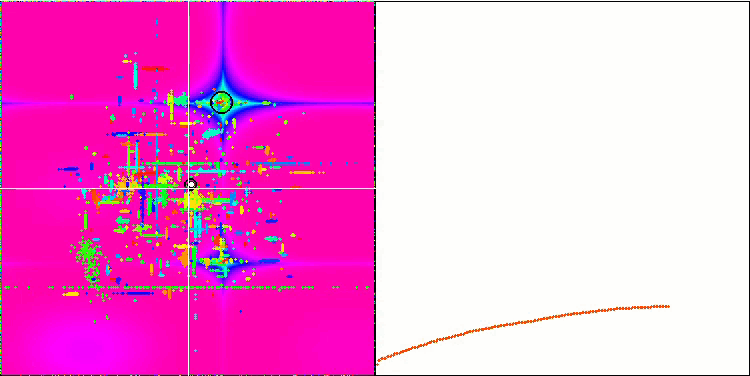
비주얼리제이션에서 '결정화'를 명확하게 볼 수 있습니다. 처음에는 백색 소음처럼 보이는 화면이 지워지고 좌표가 집중되기 시작하면서 집중의 중심이 이동합니다:

COAm의 메가시티 테스트 함수. "결정화"의 효과가 더 잘 드러납니다.
한편으로는 가변성, 즉 새로운 영역을 동적으로 검색할 수 있는 능력이 있고 다른 한편으로는 이미 극단에 도달한 좌표를 명확히 할 수 있는 능력이 있습니다. 아래는 비교를 위한 '결정화'가 뚜렷한 개미 군집 알고리즘의 애니메이션입니다:
테스트 결과
| AO | 설명 | 피부 | 숲 | 메가시티(개별) | 최종 결과 | ||||||
| 2 params(1 F) | 40 params(20F) | 1000 params(500 F) | 2 params(1 F) | 40 params(20F) | 1000 params(500 F) | 2 params(1 F) | 40 params(20F) | 1000 params(500 F) | |||
| 뻐꾸기 최적화 알고리즘 | 1.00000 | 0.85911 | 0.14316 | 0.99283 | 0.28787 | 0.04551 | 1.00000 | 0.24917 | 0.03537 | 0.51255778 | |
| 개미 군집 최적화 | 0.98229 | 0.79108 | 0.12602 | 1.00000 | 0.62077 | 0.11521 | 0.38333 | 0.44000 | 0.02377 | 0.49805222 | |
| 인공 꿀벌 군집 M | 1.00000 | 0.63922 | 0.08076 | 0.99908 | 0.20112 | 0.03785 | 1.00000 | 0.16333 | 0.02823 | 0.46106556 | |
| 인공 꿀벌 군집 | 0.99339 | 0.73381 | 0.11118 | 0.99934 | 0.21437 | 0.04215 | 0.85000 | 0.16833 | 0.03130 | 0.46043000 | |
| 회색 늑대 최적화 | 0.99900 | 0.48033 | 0.18924 | 0.83844 | 0.08755 | 0.02555 | 1.00000 | 0.10000 | 0.02187 | 0.41577556 | |
| 파티클 스웜 최적화 | 0.99627 | 0.38080 | 0.05089 | 0.93772 | 0.14540 | 0.04856 | 1.00000 | 0.09333 | 0.02233 | 0.40836667 | |
| 랜덤 | 0.99932 | 0.44276 | 0.06827 | 0.83126 | 0.11524 | 0.03048 | 0.83333 | 0.09000 | 0.02403 | 0.38163222 | |
뻐꾸기 검색 알고리즘의 장점 중 하나는 표준 랜덤 보행이 아닌 비행 또는 레비 프로세스를 사용하여 글로벌 검색을 수행한다는 점입니다. 레비 비행은 평균과 분산이 무한대이므로 COA는 표준 가우스 프로세스 알고리즘보다 더 효율적으로 검색 공간을 탐색할 수 있습니다. 레비 비행: 파워 법칙 꼬리가 있는 확률 밀도 함수에서 선택된 일련의 순간 점프를 특징으로 하는 무작위 보행 프로세스입니다.
현재 이 알고리즘은 개별 테스트에서 다른 알고리즘을 크게 능가하고 다른 "분야"에서도 크게 뒤처지지 않는 선두를 달리고 있습니다. 1000개의 인수가 있는 메가시티 불연속 함수에서 우수한 결과를 얻을 수 있어 뻐꾸기 검색은 트레이더의 작업(대부분의 경우 불연속적인 작업)에 훌륭한 도구입니다. 1000개의 인수를 가진 피부 함수에 대한 우수한(최고는 아니지만) 결과는 이 알고리즘이 특히 신경망 훈련과 일반적인 머신 러닝에 적합하다고 주장할 수 있는 근거를 제공합니다.
장점:
1. 빠른 속도.
2. 다용도성. 이 알고리즘은 다양한 최적화 문제에 사용할 수 있습니다.
3. 로컬 극한에만 집중하지 않는 기능.
4. 평활 및 이산 함수 모두에 대한 높은 컨버전스.
5. 확장 가능.
단점:
1. 여러 설정.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/11786
 새로운 기능: MQL5의 커스텀 인디케이터
새로운 기능: MQL5의 커스텀 인디케이터
 새 MetaTrader 와 MQL5를 소개해드립니다
새 MetaTrader 와 MQL5를 소개해드립니다
 VIDYA으로 트레이딩 시스템 설계하는 방법 알아보기
VIDYA으로 트레이딩 시스템 설계하는 방법 알아보기