
Нейросети — это просто (Часть 57): Стохастический маргинальный актер-критик (SMAC)
Введение
При построении автоматизированной торговой системы мы разрабатываем алгоритмы последовательного принятия решений. Именно на решение подобных задач направлены методы обучения с подкреплением. Одной из ключевых проблем в обучении с подкреплением является процесс исследования, когда Агент учится взаимодействовать с окружающей средой. В этом контексте часто используется принцип максимальной энтропии, который мотивирует Агента совершать действия с наибольшей степенью случайности. Однако на практике подобные алгоритмы обучают простых Агентов, которые изучают только локальные изменения вокруг одного действия. Это связано с необходимостью вычисления энтропии политики Агента и использования ее в качестве части цели обучения.
В то же время относительно простым подходом к увеличению выразительности политики Актера является использование латентных переменных, которые предоставляют Агенту собственную процедуру вывода для моделирования стохастичности в наблюдениях, окружающей среде и неизвестных вознаграждениях.
Введение латентных переменных в политику Агента позволяет охватить более разнообразные сценарии, совместимые с историей наблюдений. Здесь следует отметить, что политики с латентными переменными не допускают простого выражения для определения их энтропии. Наивная оценка энтропии может привести к катастрофическим сбоям при оптимизации политики. Кроме того, стохастические обновления с высокой дисперсией для максимизации энтропии не сразу различают между собой локальные случайные воздействия и многомодальное исследование.
Один из вариантов решения указанных недостатков политик с латентными переменными был предложен в статье "Latent State Marginalization as a Low-cost Approach for Improving Exploration". В ней авторы предлагают простой, но эффективный алгоритм оптимизации политики, который способен обеспечивать более эффективное и устойчивое исследование как в полностью наблюдаемых, так и в частично наблюдаемых средах.
Основные вклады указанной статьи можно кратко описать следующими тезисами:
- Мотивация использования политик с латентными переменными для улучшения исследования и устойчивости в условиях частичной наблюдаемости.
- Предлагается несколько методов стохастической оценки, сосредоточенных на эффективности исследования и уменьшении дисперсии.
- Применение подходов к методу Актер-Критик приводит к созданию алгоритма Stochastic Marginal Actor-Critic (SMAC).
1. Алгоритм SMAC
Авторы алгоритма "Stochastic Marginal Actor-Critic" предлагают использовать латентные переменные для построения распределенной политики Актера. Это простой и эффективный способ увеличения гибкости моделей и политики действий Агента. Данный подход требует минимальных изменений для внедрения в существующие алгоритмы с использованием стохастических политик поведения Агента.
Политика с латентными переменными может быть выражена следующим образом:
![]()
где st — это латентная переменная, зависящая от текущего наблюдения.
Введение латентной переменной q(st|xt) обычно увеличивает выразительность политики Актера. Это позволяет политике захватывать более широкий спектр оптимальных действий. Это может быть особенно полезно на начальной стадии исследования, когда не хватает информации о будущих вознаграждениях.
Для параметризации стохастической модели авторы метода предлагают использовать факторизованные гауссовские распределения как для политики Актера π(at|st), так и для функции латентных переменных q(st|xt). Что приводит к вычислительно эффективной политике с латентными переменными: выборка и оценка плотности остаются недорогими. Кроме того, это позволяет нам применять предложенные подходы для построения моделей на основе существующих алгоритмов со стохастическими политиками и одним гауссовским распределением. Мы просто добавляем новый стохастический узел st.
Обратите внимание, что вследствие предположения марковского процесса π(at|st) зависит только от текущего латентного состояния, хотя предложенный алгоритм легко расширяется и на не-марковские ситуации. Однако благодаря рекуррентности мы наблюдаем маргинализацию по полной скрытой истории. Ведь текущее латентное состояние st, следовательно, и политика π(at|st), является следствием ряда переходов из начального состояния под влиянием действий, совершаемых Агентом.
![]()
При этом предложенные подходы к обработке латентных переменных не зависят от того, на что влияет q.
Наличие латентных переменных делает обучение с максимальной энтропийностью довольно сложным. Ведь это требует точной оценки энтропийной составляющей. А энтропия модели с латентными переменными чрезвычайно сложна для оценки из-за трудности в маргинализации. Кроме того, использование латентных переменных приводит к увеличению дисперсии градиента. А также латентные переменные можно использовать в Q-функции для лучшей агрегации неопределенности.
В каждом из этих случаев авторы Stochastic Marginal Actor-Critic выводят обоснованные методы обработки латентных переменных. При этом конечный результат довольно прост и добавляет минимальное количество дополнительных затрат ресурсов по сравнению с политиками без латентных переменных.
В свою очередь, использование латентных переменных делает энтропию (или маргинальную энтропию) непригодной для использования из-за неразрешимости логарифма вероятности.
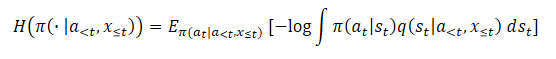
Применение наивного оценщика приведет к максимизации верхней границы на целевой функционал максимальной энтропии. Что ведет к максимизации ошибки. А это стимулирует вариационное распределение быть максимально удаленным от истинной апостериорной оценки q(st|a<t,x≤t). Кроме того, эта ошибка не ограничена и может стать произвольно большой, не оказывая фактического влияния на истинную энтропию, которую мы хотим максимизировать, что приводит к серьезным проблемам с численной неустойчивостью.
В авторской статье показаны результаты предварительного эксперимента, в котором такой подход к оценке энтропии во время оптимизации политики привел к чрезвычайно большим значениям, значительно завышая истинную энтропию и приводя к политикам, которые не обучились. Ниже представлена визуализация из авторской статьи.
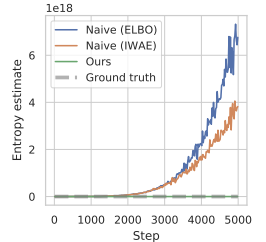
Для преодоления указанной проблемы завышения авторы метода предлагают построить оценщик нижней границы маргинальной энтропии.
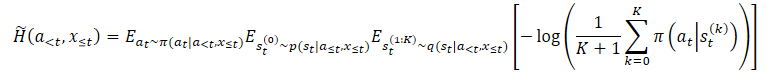
где p(st|a≤t,x≤t) — неизвестное апостериорное распределение политики.
Однако мы легко можем выбирать из него сначала st⁰, а затем выбирать at при условии st⁰. Это приводит к вложенному оценщику, при котором мы фактически выбираем K+1 раз из q(st|a<t,x≤t). Для выбора действия мы используем только первую латентную переменную st⁰. А все остальные латентные переменные используются для оценки маргинальной энтропии.
Обратите внимание, что это не эквивалентно замене ожидания внутри логарифма независимыми выборками. Предложенный оценщик монотонно возрастает с K, что в пределе становится несмещенным оценщиком маргинальной энтропии.
Вышеуказанные методы могут быть применены к общим алгоритмам максимизации энтропии. Но авторы метода создают конкретный алгоритм, который получил название "Stochastic Marginal Actor-Critic" (SMAC). SMAC характеризуется использованием политики Актера с латентными переменными и максимизацией нижней границы целевой функции маргинальной энтропии.
Алгоритм следует общепринятому стилю Актер-Критик и использует буфер воспроизведения опыта для сохранения данных, на основании которых осуществляется обновление параметров как Актера, так Критика.
Критик обучается путем минимизации ошибки:
![]()
где:
(x, a, r, x') — из буфера воспроизведения опыта D,
a' — действие Актера в соответствии с политикой π(·|x'),
Q ̅ — обозначает целевую функцию Критика,
H ̃ — оценка энтропии политики.
При этом мы оцениваем энтропию политики с латентными переменными.
Кроме того, Актер обновляется путем минимизации ошибки:
![]()
Обратите внимание, что при обновлении критика мы используем оценку энтропии политики Актера в последующем состоянии. А при обновлении политики Актера — в текущем.
В целом SMAC практически не отличается от наивного SAC с точки зрения алгоритмических деталей методов обучения с подкреплением, но получает улучшения в основном за счет структурированного поведения исследования. Что достигается благодаря моделированию латентных переменных.
2. Реализация средствами MQL5
Выше представлены теоретические выкладки авторского метода Stochastic Marginal Actor-Critic. В практической части данной статьи мы реализуем предложенный алгоритм средствами MQL5. Только мы не будем полностью повторять авторский алгоритм SMAC. В авторской статье говорится о возможности использования предложенных методов практически во всех алгоритмах обучения с подкреплением. Мы воспользуемся этой возможностью и имплементируем предложенные методы в нашу реализацию алгоритма NNM, которую мы рассмотрели в предыдущей статье.
И первые изменения будут внесены в архитектуру моделей. Как можно заметить в представленных выше формулах, основу алгоритма SMAC составляют три модели:
- q — модель представления латентного состояния;
- π — Актер;
- Q — Критик.
Думаю, последние две модели не вызывают вопросов. Первая же модель латентного состояния представляет собой Энкодер со стохастическим узлом на выходе. При этом и Актер, и Критик в качестве исходных данных используют результаты работы этого Энкодера. Здесь будет уместно вспомнить Энкодер вариационного автоэнкодера.
Имеющиеся у нас наработки позволяют нам не выносить Энкодер в отдельную модель, а оставить его, как и ранее, внутри архитектуры модели Актера. Таким образом, для реализации предложенного алгоритма нам предстоит внести изменения в архитектуру Актера. А именно, добавить стохастический узел на выходе блока предварительной обработки данных (Энкодера).
Архитектура моделей указывается в методе CreateDescriptions. По существу, мы вносим минимальные правки в архитектуру Актера. Мы оставляем блок предварительной обработки данных без изменений. Исторические данные ценового движения и индикаторов подаются на полносвязный нейронный слой. Затем они проходят первичную обработку в нейронном слое пакетной нормализации.
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!convolution) { convolution = new CArrayObj(); if(!convolution) return false; } //--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Затем нормализованные данные проходят через два последовательных сверточных слоя, в которых мы пытаемся выделить некие паттерны из структуры данных.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = BarDescr; descr.window = HistoryBars; descr.step = HistoryBars; int prev_wout = descr.window_out = HistoryBars / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
И маргинализуем состояние окружающей среды двумя полносвязными слоями.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Далее мы объединяем полученные данные с информацией о состоянии счета. И тут мы вносим первое изменение в архитектуру модели. Перед стохастическим блоком нам нужно создать слой в два раза больше латентного представления: нам нужны показатели распределения в виде средних значений и дисперсии. Поэтому размер слоя конкатенации мы указываем в два раза больше латентного представления. А за ним добавляем слой латентного состояния вариационного автоэнкодера. Именно таким слоем мы создаем стохастический узел.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 2 * LatentCount; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = LatentCount; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Обратите внимание, что мы увеличили размер нашего блока предварительной обработки данных (Энкодера). И это нам предстоит учесть при организации передачи данных между моделями.
Блок принятия решений Актера мы оставили без изменений. Он содержит три полносвязных слоя и слой латентного состояния вариационного автоэнкодера, который создает стохастичность поведения Актера.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Далее поговорим про архитектуру Критика. На первый взгляд в предложениях авторов метода SMAC нет требований к архитектуре Критика. И мы вполне бы могли оставить её без изменений. Но напомню, что мы используем декомпозированную функцию вознаграждения. И возникает вопрос: куда относить энтропию добавленного стохастического узла? Мы могли бы прибавить её к любому из имеющихся элементов вознаграждения. Но в контексте декомпозиции функции вознаграждения логичнее добавить ещё один элемент на выходе Критика. Следовательно, мы увеличиваем константу количества элементов вознаграждения.
#define NRewards 5 //Number of rewards
В остальном же архитектура модели Критика осталась без изменений.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; }
Для реализации алгоритма SMAC мы указали все необходимые модели. Но мы же внедряем предложенные методы в алгоритм NNM. Следовательно, мы оставляем все используемые ранее модели с целью сохранения полной функциональности алгоритма. Модель Случайного сверточного Кодировщика перенесена без изменений. И мы не будем на ней останавливаться. Вы самостоятельно можете с ней ознакомиться во вложении. Там же представлены все программы, используемые в данной статье.
И сразу вернемся к вопросу передачи данных между моделями. Для обращения Критика к латентному состоянию Актера мы используем идентификатор слоя латентного состояния, который указан в константе LatentLayer. Следовательно, чтобы перенаправить Критика к нужному нейронному слою в соответствии с изменением архитектуры Актера нам достаточно изменить значение указанной константы. Иные корректировки кода программы в данном контексте не требуются.
#define LatentLayer 7
Теперь давайте обсудим вопрос использования алгоритмов расчета энтропийной составляющей в функции вознаграждения. Авторы метода предложили свое видение вопроса, которое представлено в теоретической части. Однако мы расширяем свою реализацию метода NNM, в котором мы использовали ядерную норму в качестве энтропийной составляющей Актера. Для сопоставимости значений различных элементов функции вознаграждения логично использовать и для Энкодера аналогичный подход.
Авторы метода SMAC предлагают использовать K+1 семпл Энкодера для оценки энтропии латентного состояния. Очевидно, что для отдельно взятого состояния окружающей среды в процессе обучения Энкодера мы придем к некоторому среднему значению довольно быстро. И в ходе дальнейшей оптимизации параметров Энкодера мы будем стремиться уменьшить значение дисперсии для максимального разделения отдельных состояний. При снижении дисперсии в пределе к "0", энтропия также будет стремиться к "0". Получим ли мы тот же эффект при использовании ядерной нормы?
Для ответа на этот вопрос мы можем углубиться в математические формулы. А можем проверить на практике. Конечно, мы не будем сейчас создавать и долго обучать модель, чтобы проверить возможность использования ядерной нормы. Мы сделаем это гораздо проще и быстрее. Давайте создадим небольшой скрипт на Python.
Для начала импортируем две библиотеки: numpy и matplotlib. Первую будем использовать для вычислений, а вторую - для визуализации результатов.
# Импорт библиотек import numpy as np import matplotlib.pyplot as plt
Для создания семплов нам потребуются статистические показатели распределений: средние значения и соответствующие дисперсии. В процессе обучения они будут генерироваться моделью. Для тестирования подхода нам достаточно случайных значений.
mean = np.random.normal(size=[1,10]) std = np.random.rand(1,10)
Обратите внимание, что в качестве средних значений могут быть использованы любые числа. И мы генерируем их из нормального распределения. А вот дисперсии могут быть только положительные, и мы генерируем их в диапазоне (0, 1].
По аналогии со стохастическим узлом мы будем использовать трюк репараметризации распределения. Для этого сгенерируем матрицу случайных значений из нормального распределения.
data = np.random.normal(size=[20,10])
И подготовим вектор для записи наших внутренних вознаграждений.
reward=np.zeros([20])
Идея в следующем: необходимо проверить, как поведут себя внутренне вознаграждения с использованием ядерной нормы при снижении дисперсии и прочих равных условиях.
Для снижения дисперсии мы создадим вектор понижающих коэффициентов.
scl = [2**(-k/2.0) for k in range(20)]
Далее мы создаем цикл, в котором будем использовать трюк репараметризации распределения для наших случайных данных с постоянными средними и снижающейся дисперсией. На основании полученных данных рассчитаем внутреннее вознаграждение с использованием ядерной нормы. И полученные результаты сохраним в подготовленный вектор вознаграждений.
for idx, k in enumerate(scl): new_data=mean+data*(std*k) _,S,_=np.linalg.svd(new_data) reward[idx]=S.sum()/(np.sqrt(new_data*new_data).sum()*max(new_data.shape))
Результаты работы скрипта визуализируем.
# Отрисовка результатов
plt.plot(scl,reward)
plt.gca().invert_xaxis()
plt.ylabel('Reward')
plt.xlabel('STD multiplier')
plt.xscale('log',base=2)
plt.savefig("graph.png")
plt.show() 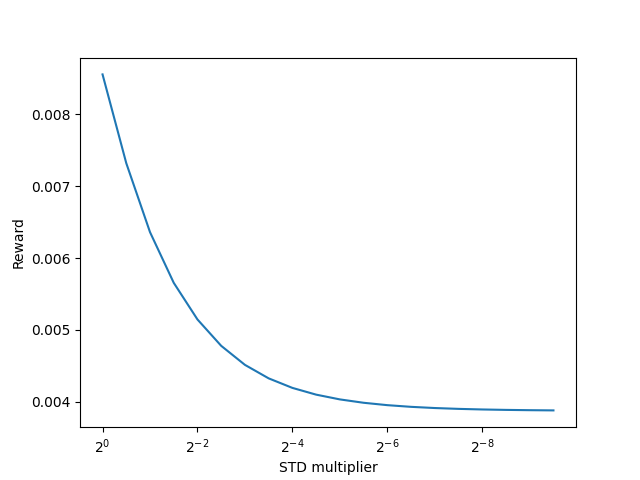
Полученные результаты наглядно демонстрируют снижение внутреннего вознаграждения с использованием ядерной нормы при снижении дисперсии распределения при прочих равных условиях. А значит, мы можем смело использовать ядерную норму и для оценки энтропии латентного состояния.
Возвращаемся к нашей реализации алгоритма средствами MQL5. И теперь мы можем приступить к реализации оценки энтропии латентного состояния. Вначале нам необходимо определить количество латентных состояний для семплирования. Данный показатель мы определим константой SamplLatentStates.
#define SamplLatentStates 32
Следующий вопрос: действительно ли нам необходимо осуществлять полный прямой проход модели Энкодера (в нашем случае Актера) для семплирования каждого латентного состояния?
Вполне очевидно, что без изменения исходных данных и параметров модели результаты работы всех нейронных слоёв будут идентичны при каждом последующем проходе. Единственное отличие - в результатах стохастического узла. Следовательно, для каждого отдельно взятого состояния нам достаточно одного прямого прохода модели Актера. А далее мы воспользуемся трюком репараметризации распределения и сэмплируем нужное нам количество скрытых состояний. Думаю, идея понятна и мы переходим к реализации.
Сначала мы генерируем матрицу случайных значений из нормального распределения со средним значением "0" и дисперсией "1". Такие показатели распределения наиболее удобны для репараметризации.
float EntropyLatentState(CNet &net) { //--- random values double random[]; Math::MathRandomNormal(0,1,LatentCount * SamplLatentStates,random); matrix<float> states; states.Assign(random); states.Reshape(SamplLatentStates,LatentCount);
Затем мы загрузим из нашей модели Актера выученные параметры распределения, которые хранятся в предпоследнем слое Энкодера. Здесь следует отметить, что нашей моделью предусмотрен один буфер данных, в котором последовательно хранятся сначала все средние значения выученного распределения, а за ними - все дисперсии. Только вот для выполнения матричных операций нам потребуется не один вектор, а две матрицы с дублированием значений по строкам. И здесь мы пойдем на небольшую хитрость. Сначала мы создаем одну большую матрицу с необходимым числом строк и двойным числом столбцов, заполненную нулевыми значениями. В первую строку запишем данные из буфера данных с параметрами распределений. А затем воспользуемся функцией накопительного суммирования значений матрицы по столбцам.
Фокус в том, что все строки, кроме первой, заполнены нулями. И в результате выполнения операции накопительного суммирования мы просто скопируем данные из первой строки во все последующие.
Теперь мы просто разделим матрицу на две равные по вертикали и получим массив матриц split. В нем матрица средних значений будет с индексом 0. А матрица дисперсий — с индексом 1.
//--- get means and std vector<float> temp; matrix<float> stats = matrix<float>::Zeros(SamplLatentStates,2 * LatentCount); net.GetLayerOutput(LatentLayer - 1,temp); stats.Row(temp,0); stats=stats.CumSum(0); matrix<float> split[]; stats.Vsplit(2,split);
Теперь мы достаточно просто осуществляем репараметризацию случайных значений из нормального распределения. И получаем нужное нам количество сэмплов.
//--- calculate latent values states = states * split[1] + split[0];
В нижнюю часть матрицы мы добавим строку с текущими значения Энкодера, которые использовались Актером и Критиками в качестве исходных данных при прямом проходе.
//--- add current latent value net.GetLayerOutput(LatentLayer,temp); states.Resize(SamplLatentStates + 1,LatentCount); states.Row(temp,SamplLatentStates);
На данном этапе у нас готовы все данные для вычисления ядерной нормы. И мы осуществляем вычисление энтропийной составляющей функции вознаграждения. Полученный результат возвращаем вызывающей программе.
//--- calculate entropy states.SVD(split[0],split[1],temp); float result = temp.Sum() / (MathSqrt(MathPow(states,2.0f).Sum() * MathMax(SamplLatentStates + 1,LatentCount))); //--- return result; }
Можно сказать, что подготовительная работа завершена. И мы переходим к работе над советниками взаимодействия с окружающей средой и обучения моделей.
Сразу скажем, что советники взаимодействия с окружающей средой (Research.mq5 и Test.mq5) остались без изменений и мы не будем на них сейчас останавливаться. А с полным кодом указанных программ, как и всех других, используемых в данной статье, вы можете ознакомиться во вложении.
А мы переходим к советнику обучения моделей и остановимся на методе обучения Train. В начале метода мы определим общий размер буфера воспроизведения опыта.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount();
А затем осуществим кодирование всех существующих примеров из буфера воспроизведения опыта с помощью случайного сверточного кодировщика. Данный процесс полностью перенесен из предыдущей реализации.
int total_states = Buffer[0].Total; for(int i = 1; i < total_tr; i++) total_states += Buffer[i].Total; vector<float> temp, next; Convolution.getResults(temp); matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size()); matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards); int state = 0; for(int tr = 0; tr < total_tr; tr++) { for(int st = 0; st < Buffer[tr].Total; st++) { State.AssignArray(Buffer[tr].States[st].state); float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1]; State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st].account[1] / PrevBalance); State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st].account[2]); State.Add(Buffer[tr].States[st].account[3]); State.Add(Buffer[tr].States[st].account[4] / PrevBalance); State.Add(Buffer[tr].States[st].account[5] / PrevBalance); State.Add(Buffer[tr].States[st].account[6] / PrevBalance); double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(!Convolution.feedForward(GetPointer(State),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } Convolution.getResults(temp); state_embedding.Row(temp,state); temp.Assign(Buffer[tr].States[st].rewards); next.Assign(Buffer[tr].States[st + 1].rewards); rewards.Row(temp - next * DiscFactor,state); state++; if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states)); Comment(str); ticks = GetTickCount(); } } }
После завершения кодирования всех примеров из буфера воспроизведения опыта мы удалим из матриц лишние строки.
if(state != total_states)
{
rewards.Resize(state,NRewards);
state_embedding.Reshape(state,state_embedding.Cols());
total_states = state;
}
Далее следует блок непосредственного обучения моделей. Здесь мы инициализируем локальные переменные и создаем цикл обучения моделей. Число итераций цикла определяется внешней переменной Iterations.
vector<float> rewards1, rewards2; int bar = (HistoryBars - 1) * BarDescr; for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
В теле цикла мы сэмплируем траекторию и отдельное состояние окружающей среды для текущей итерации обновления параметров моделей.
После чего мы проверяем пороговое значение использования целевых моделей. И, при необходимости, загружаем данные последующего состояния в соответствующие буферы данных.
target_reward = vector<float>::Zeros(NRewards); reward.Assign(Buffer[tr].States[i].rewards); //--- Target TargetState.AssignArray(Buffer[tr].States[i + 1].state); if(iter >= StartTargetIter) { float PrevBalance = Buffer[tr].States[i].account[0]; float PrevEquity = Buffer[tr].States[i].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i + 1].account[2]); Account.Add(Buffer[tr].States[i + 1].account[3]); Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- if(Account.GetIndex() >= 0) Account.BufferWrite();
Подготовленные данные используются для осуществляем прямого проход Актера и двух целевых моделей Критиков.
if(!Actor.feedForward(GetPointer(TargetState), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } //--- if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
По результатам прямого прохода целевых моделей подготовим вектор стоимости последующего состояния. И обязательно добавим в полученный вектор энтропийную оценку латентного состояния согласно алгоритму SMAC.
TargetCritic1.getResults(rewards1); TargetCritic2.getResults(rewards2); if(rewards1.Sum() <= rewards2.Sum()) target_reward = rewards1; else target_reward = rewards2; for(ulong r = 0; r < target_reward.Size(); r++) target_reward -= Buffer[tr].States[i + 1].rewards[r]; target_reward *= DiscFactor; target_reward[NRewards - 1] = EntropyLatentState(Actor); }
После подготовки вектора стоимости последующего состояния мы переходим к работе с выбранным состоянием окружающей среды. И заполняем необходимые буферы соответствующими исходными данными.
//--- Q-function study State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
Затем осуществляем прямой проход Актера для генерации латентного состояния окружающей среды.
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
На этапе обновления параметров Критиков мы используем только латентное состояние. Действия Актера мы берем из буфера воспроизведения опыта. И вызываем прямой проход обоих Критиков.
Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Обновление параметров Критиков осуществляется с учетом фактического вознаграждения от окружающей среды, скорректированного на текущую политику Актера. Параметры влияния обновленной политики Актера уже учтены в векторе стоимости последующего состояния окружающей среды.
Напомню, что мы используем декомпозированную функцию вознаграждения и для оптимизации градиентов применяется метод CAGrad. Это приводит к получению различных векторов эталонных значений для каждого Критика. Сначала мы подготавливаем вектор эталонных значений и осуществляем обратный проход первого Критика.
Critic1.getResults(rewards1); Result.AssignArray(CAGrad(reward + target_reward - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Затем повторяем операции для второго Критика.
Critic2.getResults(rewards2); Result.AssignArray(CAGrad(reward + target_reward - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Обратите внимание, что после обновления параметров каждого Критика мы осуществляем обратный проход для обновления параметров Энкодера. И не забываем на каждом этапе контролировать процесс выполнения операций.
После обновления параметров Критиков мы переходим к работе над оптимизацией модели Актера. И для определения градиента ошибки на уровне Актера мы будем использовать Критика с минимальной средней скользящей ошибкой прогнозирования стоимости действий Актера. Такой подход потенциально даст нам более точную оценку действий, генерируемых политикой Актера. И, как следствие, более корректное распределение градиента ошибки.
//--- Policy study CNet *critic = NULL; if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError()) critic = GetPointer(Critic1); else critic = GetPointer(Critic2);
Прямой проход Актера мы уже осуществили ранее. И сейчас мы сформируем прогнозное последующее состояние окружающей среды. Именно прогнозное. Ведь в буфере воспроизведения опыта есть исторические данные ценового движения и индикаторов. Они не зависят от действий Актера и мы смело их используем. А вот состояние счета напрямую зависит от выполняемых Актером торговых операций. И действия в рамках текущей политики Актера могут отличаться от сохраненных в буфере воспроизведения опыта. На данном этапе нам предстоит сформировать прогнозный вектор описания состояния счета. Для нашего удобства данный функционал уже реализован в методе ForecastAccount, который мы рассматривали в предыдущей статье. И сейчас нам достаточно лишь вызвать его с передачей корректных исходных данных.
Actor.getResults(rewards1); double cl_op = Buffer[tr].States[i + 1].state[bar]; double prof_1l = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_PROFIT) * cl_op / SymbolInfoDouble(_Symbol, SYMBOL_POINT); vector<float> forecast = ForecastAccount(Buffer[tr].States[i].account,rewards1,prof_1l, Buffer[tr].States[i + 1].account[7]); TargetState.AddArray(forecast);
Теперь, когда у нас есть все необходимые данные, мы осуществляем прямой проход выбранного Критика и Случайного сверточного Кодировщика для формирования эмбединга прогнозного последующего состояния.
if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !Convolution.feedForward(GetPointer(TargetState))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
На основании полученных данных мы формируем вектор эталонных значений функции вознаграждения для обновления параметров Актера. И обязательно корректируем градиент ошибки с использованием методики CAGrad.
next.Assign(Buffer[tr].States[i + 1].rewards); Convolution.getResults(rewards1); target_reward += KNNReward(KNN,rewards1,state_embedding,rewards) + next * DiscFactor; if(forecast[3] == 0.0f && forecast[4] == 0.0f) target_reward[2] -= (Buffer[tr].States[i + 1].state[bar + 6] / PrevBalance); critic.getResults(reward); reward += CAGrad(target_reward - reward);
После чего мы отключаем режим обновления параметров Критика и осуществляем его обратный проход. А следом - полный обратный проход Актера.
Result.AssignArray(reward); critic.TrainMode(false); if(!critic.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); critic.TrainMode(true); break; } critic.TrainMode(true);
Обязательно контролируем процесс выполнения операций. И после успешного выполнения обратного прохода обеих моделей возвращаем Критика в режим обучения.
На данном этапе мы обновили параметры обоих Критиков и Актера. Нам остается лишь обновить параметры целевых моделей Критиков. Здесь мы используем мягкое обновление параметров моделей с коэффициентом Tau, который задается во внешних параметрах советника.
//--- Update Target Nets TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau); TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
И в завершении операций в теле цикла обучения моделей мы информируем пользователя о ходе выполнения процесса обучения и переходим на следующую итерацию цикла.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
После успешного выполнения всех итераций цикла обучения моделей мы очищаем поле комментариев на графике. Выводим результаты обучения в журнал и инициализируем процесс завершения работы советника.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); ExpertRemove(); //--- }
Думаю, вы заметили, что в процессе обучения Актера мы пропустили вычисление энтропийной составляющей латентного состояния, которое предусмотрено методом SMAC. Дело в том, что мы не стали разрывать процесс формирования вектора вознаграждения на отдельные части. При построении алгоритма NNM данный процесс был вынесен в отдельный метод KNNReward. Именно в этот метод мы и внесли необходимые корректировки.
Как и ранее, в теле метода мы сначала проверяем соответствие размеров эмбединга прогнозного состояния и в матрице эмбедингов состояний окружающей среды из буфера воспроизведения опыта.
vector<float> KNNReward(ulong k, vector<float> &embedding, matrix<float> &state_embedding, matrix<float> &rewards ) { if(embedding.Size() != state_embedding.Cols()) { PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__); return vector<float>::Zeros(0); }
После успешного прохождения блока контролей мы осуществляем инициализацию необходимых локальных переменных.
ulong size = embedding.Size(); ulong states = state_embedding.Rows(); k = MathMin(k,states); ulong rew_size = rewards.Cols(); vector<float> distance = vector<float>::Zeros(states); matrix<float> k_rewards = matrix<float>::Zeros(k,rew_size); matrix<float> k_embeding = matrix<float>::Zeros(k + 1,size); matrix<float> U,V; vector<float> S;
На этом завершается этап подготовительной работы и мы переходим непосредственно к операциям вычислений. Сначала определим расстояние от прогнозного состояния до фактических примеров из буфера воспроизведения опыта.
for(ulong i = 0; i < size; i++) distance+=MathPow(state_embedding.Col(i) - embedding[i],2.0f); distance = MathSqrt(distance);
Определим k-ближайших соседей и заполним матрицу эмбедингов. А также перенесем соответствующие вознаграждения в заранее подготовленную матрицу. Одновременно вектор вознаграждений мы корректируем на коэффициент, обратный расстоянию между векторами состояний. Указанный коэффициент определит влияние вознаграждений из буфера воспроизведения опыта на результат выбранного действия Актера в соответствии с обновленной политикой поведения.
for(ulong i = 0; i < k; i++) { ulong pos = distance.ArgMin(); k_rewards.Row(rewards.Row(pos) * (1 - MathLog(distance[pos] + 1)),i); k_embeding.Row(state_embedding.Row(pos),i); distance[pos] = FLT_MAX; }
В матрицу эмбедингов последней строкой добавим эмбединг прогнозного состояния окружающей среды.
k_embeding.Row(embedding,k);
И найдем вектор сингулярных значений полученной матрицы эмбедингов. Данная операция легко выполняется с использованием встроенных матричных операций.
k_embeding.SVD(U,V,S);
Вектор вознаграждений мы формируем как среднее значение из соответствующих вознаграждений k-ближайших соседей, скорректированных на коэффициент участия.
vector<float> result = k_rewards.Mean(0);
А вот два последних элемента вектора вознаграждений мы заполняем энтропийной составляющей с использованием ядерной нормы политики Актера и латентного состояния, соответственно.
result[rew_size - 2] = S.Sum() / (MathSqrt(MathPow(k_embeding,2.0f).Sum() * MathMax(k + 1,size))); result[rew_size - 1] = EntropyLatentState(Actor); //--- return (result); }
Сформированный вектор вознаграждений возвращаем вызывающей программе. Все остальные методы советника перенесены без изменений.
На этом мы завершаем работу с советником обучения моделей. С полным его кодом, как и всех используемых в статье программ, вы можете самостоятельно ознакомиться во вложении. А мы переходим к этапу тестирования проделанной работы.
3. Тестирование
В практической части данной статьи мы проделали серьезную работу по имплементации метода Stochastic Marginal Actor-Critic в ранее реализованный советник алгоритма NNM. И теперь мы переходим на этап тестирования проделанной работы. Как всегда, обучение и тестирование моделей осуществляется на исторических данных EURUSD таймфрейм H1. Параметры всех индикаторов используются по умолчанию.
За окном уже сентябрь. И я увеличил период обучения до 7 месяцев 2023 года. Тестирование работы модели будем осуществлять на исторических данных за август 2023 года.
При создании советника обучения "...\NNM\Study.mq5" мы говорили об особенностях метода NNM и проблеме отсутствия генерируемых состояний в буфере воспроизведения опыта. Тогда мы решили уменьшить количество итераций одного цикла обучения. И сейчас мы будем придерживаться тех же подходов к процессу обучения моделей.
По аналогии с процессом обучения, используемым в предыдущей статье, мы не уменьшаем буфер воспроизведения опыта в целом. Но в то же время, буфер воспроизведения опыта мы будем заполнять постепенно. На первой итерации мы запускаем советник сбора обучающих данных на 100 проходов. На указанном историческом интервале это уже дает нам почти 360К состояний для обучения моделей.
После первой итерации обучения моделей мы дополняем базу примеров еще на 50 проходов. Таким образом мы постепенно заполняем буфер воспроизведения опыта новыми состояниями, которые соответствуют действиям Актера в рамках обучаемой политики.
Процесс обучения моделей и сбора дополнительных примеров мы повторяем несколько раз до достижения желаемого результата обучения политики Актера.
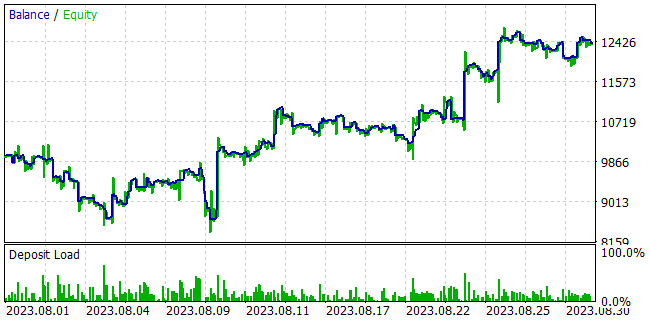
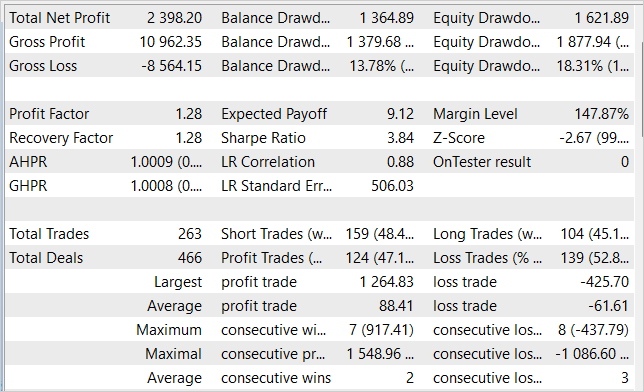
В процессе обучения моделей нам удалось получить политику Актера, способную генерировать прибыль на обучающей выборке и обобщать полученные знания на последующие состояния окружающей среды. Так, в тестере стратегий обученная нами модель за 1 месяц, следующий за обучающей выборкой, смогла сгенерировать прибыль в размере 23,98%. За период тестирования модель совершила 263 торговых операции, 47% из которых были закрыты с прибылью. Максимальная прибыль на одну сделку почти в 3 раза превышает максимальную убыточную сделку. А средняя прибыль на одну сделку на 44% процента превышает средний убыток. Все это в совокупности позволило получить профит-фактор на уровне 1,28. При этом на графике линии баланса мы наблюдаем четкую тенденцию к росту.
Заключение
В статье мы познакомились с методом Stochastic Marginal Actor-Critic, который представляет собой инновационный подход к решению задач обучения с подкреплением. Основываясь на принципе максимальной энтропии, SMAC позволяет агенту исследовать окружающую среду более эффективно и обучаться более устойчиво, что достигается введением дополнительного стохастического узла латентных переменных.
Использование латентных переменных в политике Агента позволяет значительно увеличить его выразительность и способность моделировать стохастичность в наблюдениях и наградах.
Однако существуют некоторые сложности в обучении политики с латентными переменными. И авторы метода предлагают решения, позволяющие справляться с этими трудностями.
В практической части статьи мы успешно интегрировали SMAC в архитектуру метода NNM, создав простой и эффективный метод оптимизации политики, что подтверждается результатами тестирования. Нам удалось обучить политику Актера, способную генерировать доходность до 24% в месяц.
С учетом этих результатов метод SMAC представляет собой эффективное решение для решения практических задач.
Однако хочу обратить внимание, что все представленные программы в статье созданы лишь для демонстрации метода и не пригодны к работе на реальных счетах. Им требуются дополнительная настройка и оптимизация функционала.
Напомню, что финансовые рынки являются высокорискованным видом инвестиций. И все риски от операций, совершаемых вами или электронными средствами, которые вы используете, лежат полностью в вашей ответственности.
Ссылки
- Latent State Marginalization as a Low-cost Approach for Improving Exploration
- Нейросети — это просто (Часть 56): Использование ядерной нормы для стимулирования исследования
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | Study.mq5 | Советник | Советник обучения агента |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
- Бесплатные приложения для трейдинга
- Форексный VPS бесплатно на 24 часа
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Доброго времени.
Дмитрий, спасибо за вашу работу.
Хочу уточнить для всех...
То что Дмитрий выкладывает это не "Грааль"
это Классический пример академической ЗАДАЧИ, которая предполагает подготовку к научно исследовательской деятельности теоретико-методического характера.
А все хотят видеть на своём счету, прямо здесь и сейчас, положительный результат...
Дмитрий учит нас, как решить (нашу/мою/твою/его) задачу всеми представленными, Дмитрием методами.
Популярные ИИ (GPT) имеют более 700 Миллионов параметров!!!! А сколько данная ИИ?
Если хотите получить хороший результат, обменивайтесь идеями (добавляйте параметры), приводите результаты тестирований и т.д.
Создайте отдельный ЧАТ и там "получайте" результат. Хвастаться можно тут :-), тем самым покажите эффективность работы Дмитрия...
Доброго времени.
Дмитрий, спасибо за вашу работу.
Хочу уточнить для всех...
То что Дмитрий выкладывает это не "Грааль"
это Классический пример академической ЗАДАЧИ, которая предполагает подготовку к научно исследовательской деятельности теоретико-методического характера.
А все хотят видеть на своём счету, прямо здесь и сейчас, положительный результат...
Дмитрий учит нас, как решить (нашу/мою/твою/его) задачу всеми представленными, Дмитрием методами.
Популярные ИИ (GPT) имеют более 700 Миллионов параметров!!!! А сколько данная ИИ?
Если хотите получить хороший результат, обменивайтесь идеями (добавляйте параметры), приводите результаты тестирований и т.д.
Создайте отдельный ЧАТ и там "получайте" результат. Хвастаться можно тут :-), тем самым покажите эффективность работы Дмитрия...
Друг, тут никто не ждёт грааля! Я вот просто хотел бы увидеть, что то что выкладывает Дмитрий в действительности работает. Не со слов Дмитрия в его статьях (у него во всех статьях практически положительный результат), а у себя на компе. Вот я скачал его советник допустим с этой статьи и провёл уже 63 цикла обучения (досбор данных -> тренировка). И она до сих пор льёт в минус. За все 63 цикла было только пара сборов данных, когда из 50 новых примеров было 5-6 положительных. Всё остальное в минус. Как мне увидеть что это действительно работает?
Я Дмитрия спросил выше сообщением, он ничего не ответил. Такая же проблема и в других статьях - сколько не тренируй результата нет....
Друг если у тебя получился стабильный результат, то напиши сколько ты сделал циклов до стабильного результата допустим в этой статье? Если изменять, то что изменять чтобы увидеть результат у себя на компе, просто в тестере? Не грааль, а хотя бы увидеть что это работает...?
Good time.
Dmitry, thank you for your work.
I want to clarify for everyone ...
The fact that Dmitry lays out this is not the "Grail"
This is a classic example of an academic TASK, which involves preparation for research activities of a theoretical and methodological nature.
And everyone wants to see a positive result on their account, right here and now...
Dmitry teaches us how to solve (our/my/your/his) problem with all the methods presented by Dmitry.
Popular AI (GPT) has more than 700 Million parameters!!! And how much is this AI?
If you want to get a good result, exchange ideas (add parameters), give test results, etc.
Create a separate CHAT and "get" the result there. You can brag here :-), thereby showing the effectiveness of Dmitry's work ...
Here are the Params: (based on Dmitry and some research.)
#include "FQF.mqh"
The length of the message should not exceed 64000 characters
===I CUT THE LAST PARTS as Comments are limited to 64000 Chars but you know what to do... =)
The length of the message should not exceed 64000 characters
Для вставки кода нужно применять соответствующую кнопку
С уважением, Владимир.