
Neuronale Netze leicht gemacht (Teil 37): Sparse Attention (Verringerte Aufmerksamkeit)
Einführung
Im vorigen Artikel haben wir relationale Modelle erörtert, die in ihrer Architektur Aufmerksamkeitsmechanismen verwenden. Wir haben dieses Modell verwendet, um einen Expert Advisor zu erstellen, und der resultierende EA zeigte gute Ergebnisse. Wir haben jedoch festgestellt, dass die Lernrate des Modells im Vergleich zu unseren früheren Experimenten niedriger war. Dies ist darauf zurückzuführen, dass der im Modell verwendete Transformatorblock eine recht komplexe architektonische Lösung ist, die eine große Anzahl von Operationen ausführt. Die Anzahl dieser Operationen wächst quadratisch mit der Größe der analysierten Sequenz, was zu einem Anstieg des Speicherverbrauchs und der Trainingszeit des Modells führt.
Wir sind uns jedoch darüber im Klaren, dass nur begrenzte Mittel zur Verbesserung des Modells zur Verfügung stehen. Daher ist es notwendig, das Modell mit minimalen Qualitätsverlusten zu optimieren.
1. Sparse Attention (Verringerte Aufmerksamkeit)
Wenn wir über die Optimierung der Leistung eines Modells sprechen, müssen wir uns zunächst mit seinen Hyperparametern befassen. Der Satz solcher Parameter sollte unter Berücksichtigung des Ressourcenverbrauchs und der Modellqualität optimal sein. Die Erhöhung der Anzahl der Neuronen in einer Schicht ab einem bestimmten Schwellenwert führt praktisch nicht zu einer Verbesserung der Modellqualität. Dasselbe gilt für die Anzahl der neuronalen Schichten. Die Menge der optimalen Hyperparameter hängt jedoch von der jeweiligen Aufgabe und ihrer Komplexität ab.
All dies gilt für die Anzahl der Aufmerksamkeitsköpfe (attention heads) im mehrköpfigen Self-Attention-Block. Manchmal reichen zwei Köpfe aus, um gute Ergebnisse zu erzielen, aber das ist nicht der optimale Wert für alle Probleme. Alle Hyperparameter müssen experimentell für jede spezifische Aufgabe und Modellarchitektur ausgewählt werden.
In diesem Artikel werden architektonische Ansätze zur Reduzierung der Anzahl von Operationen im Self-Attention-Block erörtert. Bevor wir jedoch zur Optimierung des Algorithmus übergehen, ist es wichtig, sich daran zu erinnern, wie der Self-Attention-Block funktioniert.
Zunächst werden drei Einheiten berechnet: Query, Key und Value (Abfrage, Schlüssel und Wert) für jedes Element der Sequenz. Zu diesem Zweck wird der Vektor, der das Sequenzelement beschreibt, mit der entsprechenden Gewichtsmatrix multipliziert. Dann multiplizieren wir die Query-Matrix mit der transponierten Key-Matrix, um die Abhängigkeitskoeffizienten zwischen den Elementen der Sequenz zu erhalten. Diese Koeffizienten werden dann mit der SoftMax-Funktion normalisiert.
![]()
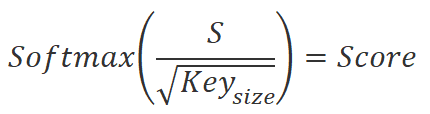
Nach der Normalisierung der Abhängigkeitskoeffizienten multiplizieren wir sie mit der Value-Matrix, um die Ausgangswerte für jedes Element der Sequenz zu erhalten. Diese Ausgabewerte sind gewichtete Summen von Elementwerten, die die Bedeutung der einzelnen Elemente im Kontext des Problems berücksichtigen.
![]()
Eine Erhöhung der Anzahl von Sequenzelementen führt zu einer Erhöhung der Rechenkomplexität von Operationen in Algorithmen, die Aufmerksamkeitsmechanismen verwenden. Dies ist darauf zurückzuführen, dass in jeder Phase die Operationen der Entitätsberechnung, der Matrixmultiplikation und der Normalisierung der Abhängigkeitskoeffizienten für jedes Element der Sequenz durchgeführt werden.
Wenn eine Sequenz zu viele Elemente hat, kann dies zu einem erheblichen Anstieg der Berechnungszeit und der Kosten für Rechenressourcen führen. Um den Algorithmus zu optimieren und die Anzahl der Berechnungen in jeder Phase zu verringern, können wir verschiedene Methoden anwenden, darunter auch die Sparse Attention (Verringerte Aufmerksamkeit). Diese Methode wurde von Rewon Child in dem Artikel „Generating Long Sequences with Sparse Transformers“ vorgeschlagen, der im April 2019 veröffentlicht wurde.
Sparse Attention ist eine Technik zur Optimierung des Aufmerksamkeitsmechanismus, um den Rechenaufwand für die Verarbeitung der Elemente einer Sequenz zu verringern.
Die Methode beruht darauf, dass nur die wichtigsten Elemente der Sequenz bei der Berechnung der Aufmerksamkeitskoeffizienten zwischen ihnen berücksichtigt werden. Anstatt die Aufmerksamkeitskoeffizienten für alle Paare von Elementen in einer Sequenz zu berechnen, wählen wir also nur die wichtigsten Paare aus.
Einer der Vorteile der Sparse-Attention-Methode besteht darin, dass sie die Anzahl der Berechnungen, die zur Verarbeitung der Elemente der Sequenz erforderlich sind, erheblich reduzieren kann. Dies ist besonders wichtig bei der Verarbeitung großer Sequenzen, bei denen die Anzahl der Berechnungen sehr hoch sein kann.
Darüber hinaus kann Sparse Attention dazu beitragen, das Problem der „Aufmerksamkeit auf alles“ zu bekämpfen, wenn der Aufmerksamkeitsmechanismus die Aufmerksamkeit gleichmäßig auf alle Elemente der Sequenz verteilt, was zu einer ineffizienten Nutzung der Ressourcen führt und den Algorithmus verlangsamt.
Bei der Implementierung von Sparse Attention können verschiedene Ansätze verfolgt werden. Die eine besteht darin, die Sequenz in Blöcke aufzuteilen und die Aufmerksamkeit nur zwischen Elementen innerhalb jedes Blocks und zwischen Elementen verschiedener Blöcke zu berechnen. In diesem Fall können nur die Elemente mit dem geringsten Abstand berücksichtigt werden, um die Anzahl der Berechnungen zu verringern.
Ein anderer Ansatz ist die Auswahl der wichtigsten Elemente in einer Sequenz auf der Grundlage ihrer Ähnlichkeit. Dazu können verschiedene Clustermethoden verwendet werden.
Ein dritter Ansatz ist die Verwendung von Heuristiken und Algorithmen zur Auswahl der wichtigsten Elemente in einer Sequenz, z. B. auf der Grundlage ihrer Häufigkeit, ihrer Bedeutung oder ihres Kontexts.
Die Autoren stellen fest, dass Sparse Attention nur dann effektiv funktioniert, wenn ein Algorithmus zur Verteilung der Sequenzelemente in Blöcke verwendet wird, der für jeden Aufmerksamkeitskopf eine andere Blockstruktur vorsieht. Auf diese Weise können Sie den Einfluss der einzelnen Elemente der Sequenz genauer bestimmen und die Effizienz des Algorithmus verbessern.
Sparse Attention kann in verschiedenen Bereichen des maschinellen Lernens und der Verarbeitung natürlicher Sprache eingesetzt werden, z. B. bei der maschinellen Übersetzung, der Texterzeugung, der Stimmungsanalyse und vielen anderen. In dem oben genannten Artikel stellen die Autoren der Methode die Ergebnisse der Anwendung des Algorithmus auf Texte, Bilder und Audioaufnahmen vor.
Darüber hinaus kann Sparse Attention effektiv mit anderen Techniken zur Optimierung der Aufmerksamkeitssteuerung kombiniert werden, um genauere Ergebnisse bei der Verarbeitung von Sequenzen zu erzielen.
Trotz ihrer Wirksamkeit hat die Sparse Attention-Methode auch ihre Nachteile. Eine davon ist, dass die Auswahl der wichtigsten Elemente in der Sequenz falsch sein kann, was zu Informationsverlusten führen kann. Daher ist es notwendig, die geeignete Methode für jede spezifische Aufgabe zu wählen und die Parameter des Algorithmus sorgfältig abzustimmen.
Ich glaube, dass die Sparse Attention-Methode für die Lösung von Problemen im Zusammenhang mit der Finanzmarktanalyse nützlich sein kann. Bei der Analyse der Kursentwicklung von Finanzsymbolen müssen wir die Daten oft sehr tiefgehend analysieren, und oft haben nur einzelne Elemente dieser Historie Auswirkungen auf die aktuelle Situation. Durch die Verwendung der Sparse Attention-Methode wird die Menge an Rechenressourcen reduziert, die für die Auswahl signifikanter Datenblöcke zur Untersuchung benötigt werden. Die Methode wird auch dazu beitragen, unbedeutende Elemente aus weiteren Operationen zu eliminieren, was die Effizienz der Finanzmarktanalyse erhöhen wird.
Finanzmarktkurse haben jedoch eine variable Struktur, sodass wir nicht mit festen Blöcken von Elementen in der analysierten Sequenz arbeiten können. Um den Modelllernprozess zu beschleunigen, können wir die Heuristik der „80/20“-Pareto-Regel anwenden, bei der wir nur 20 % der wichtigsten Elemente aus der gesamten Sequenz nehmen. Die Bedeutung der Elemente wird auf der Grundlage der Abhängigkeitskoeffizienten zwischen den Elementen bestimmt, die mit den ersten beiden oben beschriebenen Formeln berechnet werden. Bereits nach der ersten Iteration, vor der Normalisierung der Daten, ist es möglich, die wichtigsten Elemente der Sequenz genau zu identifizieren und die restlichen Elemente von weiteren Operationen auszuschließen. Dadurch wird die Anzahl der Operationen in den Phasen der Normalisierung und der Ermittlung der Ergebnisse des Self-Attention-Blocks reduziert.
Da jeder Aufmerksamkeitskopf seine eigenen einzigartigen Matrizen zur Bestimmung der Abfrage und des Schlüssels verwendet, ist es wahrscheinlich, dass die ausgewählten Elemente in jedem Aufmerksamkeitskopf unterschiedlich sind.
Nachdem wir nun die Hauptrichtungen für die Optimierung des Algorithmus festgelegt haben, können wir zu seiner Implementierung in der Sprache MQL5 übergehen.
2. Implementierung mittels MQL5
Um die vorgeschlagene Methode zu implementieren, wird eine neue neuronale Schichtklasse CNeuronMLMHSparseAttention erstellt. Natürlich werden wir nicht alle Methoden der Klasse neu erstellen. Stattdessen werden wir sie von der bestehenden Klasse CNeuronMLMHAttentionOCL ableiten. Und hier wollen wir analysieren, welche Klassenmethoden und OpenCL-Programmkerne geändert werden müssen, um die vorgeschlagene Optimierung zu implementieren.
Wie bereits erwähnt, betrifft unsere erste Änderung des Algorithmus den Block zur Bestimmung der Abhängigkeitskoeffizienten. Diese Werte werden in einem direkten Durchlauf im MHAttentionScore-Kernel ermittelt. Für unsere Implementierung werden wir den angegebenen Kernel durch MHSparseAttentionScore ersetzen.
In den Kernel-Parametern der übergeordneten Klasse haben wir Zeiger auf zwei Datenpuffer übergeben: einen verketteten Tensor der Entitäten Query, Key und Value als Quelldaten und einen Puffer zum Schreiben der Operationsergebnisse in Form von Abhängigkeitskoeffizienten. Zusätzlich zu den Datenpuffern wurde die Dimension der internen Entitäten an den Kernel übergeben. Jetzt fügen wir den Geringfügigkeitskoeffizienten „sparse“ hinzu. Wir geben einen Wert im Bereich von 0 bis 1 ein, der den Anteil der ausgewählten Sequenzelemente mit dem größten Einfluss auf das analysierte Element angibt.
__kernel void MHSparseAttentionScore(__global float *qkv, ///<[in] Matrix of Querys, Keys, Values __global float *score, ///<[out] Matrix of Scores int dimension, ///< Dimension of Key float sparse ///< less than 1.0 coefficient of sparse ) { int q = get_global_id(0); int h = get_global_id(1); int units = get_global_size(0); int heads = get_global_size(1); //---
Der neue Kernel arbeitet, wie der Kernel der übergeordneten Klasse, in einem zweidimensionalen Aufgabenraum. Die erste Dimension gibt die Ordnungszahl des zu analysierenden Sequenzelements an, und die zweite Dimension entspricht dem verwendeten Aufmerksamkeitskopf. Im Kernelkörper speichern wir die globalen Bezeichner des laufenden Threads sofort in lokalen Variablen.
Als Nächstes werden wir ein wenig Vorarbeit leisten, indem wir die notwendigen lokalen Variablen deklarieren und den Offset in den Datenpuffern zu den zu analysierenden Elementen bestimmen.
int shift_q = dimension * (h + 3 * q * heads); int shift_s = units * (h + q * heads); int active_units = (int)max((float)(units * sparse), min((float)units, 3.0f)); //--- float koef = sqrt((float)dimension); if(koef < 1) koef = 1; float sum = 0.0f; float min_s = 0.0f; float max_s = 0.0f;
Wir bestimmen auch den absoluten Wert der ausgewählten Elemente. Bitte beachten Sie, dass ich bei der Festlegung der Anzahl der auszuwählenden signifikanten Sequenzelemente eine Grenze gesetzt habe: Es können nicht weniger als drei Elemente sein. Dadurch wird vermieden, dass der Aufmerksamkeitsblock bei kleinen Sequenzen unnötig deaktiviert wird. Wir wissen, dass der maximale Abhängigkeitskoeffizient fast immer von den analysierten Elementen für ihren eigenen Schlüssel erzeugt wird.
Als Nächstes implementieren wir eine Schleife, in der wir den Abfragevektor des analysierten Elements mit der Schlüsselmatrix multiplizieren. Im Schleifenkörper werden wir auch die Maximal- und Minimalwerte des resultierenden Vektors bestimmen.
for(int k = 0; k < units; k++) { float result = 0; int shift_k = dimension * (h + heads * (3 * k + 1)); for(int i = 0; i < dimension; i++) { if((dimension - i) > 4) { result += dot((float4)(qkv[shift_q + i], qkv[shift_q + i + 1], qkv[shift_q + i + 2], qkv[shift_q + i + 3]), (float4)(qkv[shift_k + i], qkv[shift_k + i + 1], qkv[shift_k + i + 2], qkv[shift_k + i + 3])); i += 3; } else result += (qkv[shift_q + i] * qkv[shift_k + i]); } score[shift_s + k] = result; if(k == 0) min_s = max_s = result; else { max_s = max(max_s, result); min_s = min(min_s, result); } }
Um die Abhängigkeiten zwischen den erhaltenen Werten und den entsprechenden Elementen der Sequenz zu erhalten, sortieren wir den Vektor nicht, um die wichtigsten Elemente auszuwählen. Stattdessen erhöhen wir iterativ die untere Grenze des Signifikanzbereichs der Abhängigkeitskoeffizienten, bis wir die erforderliche Anzahl von „wichtigen“ Elementen der Sequenz erhalten. Diese Funktionweise wird in der folgenden Schleife implementiert.
int count = units; float temp = max_s; while(count > active_units) { count = 0; for(int k = 0; k < units; k++) { float value = score[shift_s + k]; if(value < min_s) continue; count++; if(value < temp && value > min_s) temp = value; } if(count > active_units) min_s = temp; }
Nach der Bestimmung des Signifikanzbereichs geht man zum nächsten Schritt über, der Datennormalisierung, die aus zwei Schritten besteht. Im ersten Schritt berechnen wir die exponentiellen Werte der Abhängigkeitsniveaus, die wir im vorherigen Schritt erhalten haben. Anschließend werden diese Werte durch die Gesamtsumme geteilt. Aber wir sollten uns an den von uns festgelegten Bedeutungsbereich erinnern. Daher setzen wir die Abhängigkeitskoeffizienten für Elemente außerhalb dieses Bereichs auf Null und schließen sie somit von weiteren Operationen aus. Dies gilt sowohl für die Exponentialberechnung als auch für den Normalisierungsschritt.
if(max_s == 0.0f) max_s = 1.0f; for(int k = 0; k < units; k++) { float value = score[shift_s + k]; if(value < min_s) { score[shift_s + k] = 0.0f; continue; } value = exp(value / max_s / koef); score[shift_s + k] = value; sum += value; } for(int k = 0; (k < units && sum > 1); k++) { temp = score[shift_s + k]; if(temp == 0.0f) continue; score[shift_s + k] = temp / sum; } }
Als Ergebnis der Operationen des spezifizierten Kerns erhalten wir nur eine kleine Anzahl von Nicht-Null-Abhängigkeitskoeffizienten für ausgewählte Elemente der analysierten Sequenz, mit denen wir weiter arbeiten werden. Wir schließen auch Elemente der Sequenz mit Null-Abhängigkeitskoeffizienten von weiteren Vorwärts- und Rückwärtsdurchläufen aus.
Der nächste Schritt besteht darin, den Ausgang des Aufmerksamkeitsblocks zu erhalten. Dazu muss nach dem Self-Attention-Algorithmus die „Score“-Matrix der normalisierten Abhängigkeitskoeffizienten mit der „Value“-Matrix der Entitäten multipliziert werden. Dieser Vorgang ist im MHSparseAttentionOut-Kernel implementiert. In diesem Kernel wird auch auf Nullabhängigkeitskoeffizienten geprüft, um die Anzahl der durchgeführten Operationen zu reduzieren.
In den Kernel-Parametern werden Zeiger auf 3 Datenpuffer übergeben. Der verkettete Tensor der Query-, Key- und Value-Entitäten bildet zusammen mit der „Score“-Matrix der Abhängigkeitskoeffizienten die Ausgangsdaten für die durchzuführenden Operationen. Das Ergebnis der Operationen wird in den Out-Puffer geschrieben. Die Dimension des Schlüsselvektors eines Elements der Sequenz wird ebenfalls in Parametern übergeben. Wie wir bereits gesehen haben, verwenden wir in der mehrköpfigen Aufmerksamkeitsklasse Vektoren mit der gleichen Dimension für die internen Entitäten Query, Key und Value.
__kernel void MHSparseAttentionOut(__global float *scores, ///<[in] Matrix of Scores __global float *qkv, ///<[in] Matrix of Values __global float *out, ///<[out] Output tensor int dimension ///< Dimension of Value ) { int u = get_global_id(0); int units = get_global_size(0); int h = get_global_id(1); int heads = get_global_size(1);
Dieser Kernel wird wie der vorherige in einem zweidimensionalen Aufgabenraum aufgerufen, um die einzelnen Arbeitsabläufe nach Sequenzelementen und Aufmerksamkeitsköpfen zu trennen. Zu Beginn des Kernels speichern wir Thread-Identifikatoren in lokalen Variablen.
Als Nächstes definieren wir Offsets in den Datenpuffern.
int shift_s = units * (h + heads * u); int shift_out = dimension * (h + heads * u);
Danach erstellen wir ein System von verschachtelten Schleifen, um den Vektor der Abhängigkeitskoeffizienten mit der Wertmatrix zu multiplizieren. An dieser Stelle fügen wir eine Null-Abhängigkeitsfaktor-Prüfung ein, um redundante Operationen zu vermeiden.
for(int d = 0; d < dimension; d++) { float result = 0; for(int v = 0; v < units; v ++) { float cur_score = scores[shift_s + v]; if(cur_score == 0) continue; int shift_v = dimension * (h + heads * (3 * v + 2)) + d; result += cur_score * qkv[shift_v]; } out[shift_out + d] = result; } }
Damit ist unsere Arbeit mit den Kerneln des Vorwärtsdurchlaufs unserer neuen Klasse abgeschlossen. Schauen wir uns nun den Umfang der Änderungen im Teil des Rückwärtsdurchlaufs an.
Der Rückwärtsdurchlauf des Self-Attention-Blocks wurde im MHAttentionInsideGradients-Kernel implementiert. Der Algorithmus ermöglicht es Ihnen, die erforderlichen Kontrollpunkte entlang des bestehenden Kerns hinzuzufügen, ohne ein Duplikat davon zu erstellen. Ich schlage vor, den konstruierten Algorithmus und die ihm hinzugefügten Kontrollpunkte zu betrachten.
In den Kernel-Parametern werden wir Zeiger auf 5 Datenpuffer übergeben:
- Verketteter Tensor der Werte von Query, Key and Value (qkv)
- Verketteter Tensor zum Schreiben der Fehlergradienten von Query, Key and Value (qkv_g)
- Matrix der Abhängigkeitskoeffizienten (Scores)
- Matrix zum Schreiben von Fehlergradienten auf der Ebene der Abhängigkeits-Koeffizientenmatrix (scores_g)
- Tensor der Fehlergradienten auf der Ausgangsebene des aktuellen Aufmerksamkeitsblocks.
__kernel void MHAttentionInsideGradients(__global float *qkv, __global float *qkv_g, __global float *scores, __global float *scores_g, __global float *gradient, int dimension) { int u = get_global_id(0); int h = get_global_id(1); int units = get_global_size(0); int heads = get_global_size(1); float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
Wir werden den Kernel der Fehlergradientenverteilung in einem 2-dimensionalen Raum von Problemen, wie die beiden zuvor betrachteten, nennen. Eine Dimension bezeichnet das zu analysierende Sequenzelement. Die zweite Dimension gibt den aktuellen Aufmerksamkeitsschwerpunkt an. Anhand dieser Bezeichner können wir den Versatz in den Datenpuffern zu den benötigten Elementen bestimmen. Daher speichern wir zu Beginn des Kernels diese Thread-Identifikatoren in lokalen Variablen.
Außerdem ist der Kernel-Algorithmus bedingt in zwei Blöcke unterteilt. In der ersten definieren wir den Fehlergradienten auf der Ebene der Abhängigkeitskoeffizientenmatrix. Hier implementieren wir eine Schleife zum Sammeln von Gradienten für den Vektor der Abhängigkeits-Koeffizienten des analysierten Elements der Sequenz. Da die nicht verwendeten Elemente der Sequenz mit Null-Abhängigkeitskoeffizienten das Endergebnis nicht beeinflusst haben, sollte der Fehlergradient für sie gleich Null sein. Daher wird im Schleifenkörper zunächst der aktuelle Abhängigkeitskoeffizient überprüft. Wenn ein Nullwert erkannt wird, wird einfach zum nächsten Element übergegangen.
Es ist wichtig zu wissen, dass der Zugriff auf den globalen Speicher, in dem die Elemente aller unserer Datenpuffer gespeichert sind, eine relativ teure Operation ist. In unserem Fall handelt es sich bei dem Vektor der Fehlergradienten auf der Ebene der Sequenzkoeffizientenmatrix um einen temporären Speicher, der in anderen Kernen nicht verwendet wird. Wir weisen dem nicht einmal die Null zu, da dies eine unnötige Operation ohne großen Nutzen wäre.
//--- Calculating score's gradients uint shift_s = units * (h + u * heads); for(int v = 0; v < units; v++) { float s = scores[shift_s + v]; if(s <= 0) continue; float sg = 0; int shift_v = dimension * (h + heads * (3 * v + 2)); int shift_g = dimension * (h + heads * v); for(int d = 0; d < dimension; d++) sg += qkv[shift_v + d] * gradient[shift_g + d]; scores_g[shift_s + v] = sg * (s < 1 ? s * (1 - s) : 1) / koef; } barrier(CLK_GLOBAL_MEM_FENCE);
Im nächsten Schritt verteilen wir den Fehlergradienten auf die internen Entitäten Query, Key und Value. Wir bestimmen zunächst den Offset in den Datenpuffern und erstellen dann ein System von Schleifen, um Fehlergradienten zu sammeln.
Hier wird in einer verschachtelten Schleife der Abhängigkeitskoeffizient geprüft, und wenn wir einen Nullwert finden, gehen wir einfach zum nächsten Element über. Dadurch werden unnötige Vorgänge vermieden.
//--- Calculating gradients for Query, Key and Value uint shift_qg = dimension * (h + 3 * u * heads); uint shift_kg = dimension * (h + (3 * u + 1) * heads); uint shift_vg = dimension * (h + (3 * u + 2) * heads); for(int d = 0; d < dimension; d++) { float vg = 0; float qg = 0; float kg = 0; for(int l = 0; l < units; l++) { float sg = scores[shift_s + l]; if(sg <= 0) continue; uint shift_q = dimension * (h + 3 * l * heads) + d; uint shift_k = dimension * (h + (3 * l + 1) * heads) + d; uint shift_g = dimension * (h + heads * l) + d; //--- vg += gradient[shift_g] * sg; sg = scores_g[shift_s + l]; kg += sg * qkv[shift_q]; qg += sg * qkv[shift_k]; } qkv_g[shift_qg + d] = qg; qkv_g[shift_kg + d] = kg; qkv_g[shift_vg + d] = vg; } }
Nachdem alle Iterationen dieses Kerns abgeschlossen sind, erhalten wir Fehlergradienten auf der Ebene von Query, Key and Value, die dann auf die entsprechenden Gewichtsmatrizen und die vorherige neuronale Schicht verteilt werden.
Damit ist die Arbeit an den Kerneln des OpenCL-Programms abgeschlossen und wir können mit der Arbeit am Code des Hauptprogramms fortfahren. Wir haben zwei Kerne hinzugefügt. Daher müssen wir die Kernel-Aufrufe in das Hauptprogramm aufnehmen. Erstellen wir zunächst Konstanten für den Zugriff auf die Kernel.
Achten Sie darauf, dass wir Konstanten für die Arbeit mit zwei Kerneln und nur einer Parameterkonstante erstellen. Wir haben die Kernel auf der Grundlage bestehender Kernel erstellt und die Struktur der Parameter der Basiskernel fast vollständig übernommen. Daher können wir während des Betriebs der Kernel vorhandene Konstanten verwenden. Wir erstellen nur eine Konstante, um den Geringfügikeitsparameter anzugeben.
#define def_k_MHSparseAttentionScore 44 ///< Index of the kernel of the multi-heads sparse attention neuron // to calculate score matrix (#MHSparseAttentionScore) #define def_k_mhas_sparse 3 ///< less than 1.0 coefficient of sparse //--- #define def_k_MHSparseAttentionOut 45 ///< Index of the kernel of the multi-heads sparse attention neuron // to calculate multi-heads out matrix (#MHSparseAttentionOut)
Als Nächstes müssen wir die Erstellung von Kerneln im OpenCL-Kontext implementieren. Wir müssen die Gesamtzahl der aktiven Kernel im Kontext auf 46 erhöhen und die Kernel-Erstellungsmethoden aufrufen.
opencl.SetKernelsCount(46); if(!opencl.KernelCreate(def_k_MHSparseAttentionScore, "MHSparseAttentionScore")) { PrintFormat("Error of create kernell: %d line %d", GetLastError(), __LINE__); return false; } if(!opencl.KernelCreate(def_k_MHSparseAttentionOut, "MHSparseAttentionOut")) { PrintFormat("Error of create kernell: %d line %d", GetLastError(), __LINE__); return false; }
Beachten Sie, dass wir die oben genannten Vorgänge zur Erstellung von Kerneln im OpenCL-Kontext in drei Methoden der Dispatch-Klasse des neuronalen Netzes CNet wiederholen müssen. Das ist nicht sehr praktisch. Daher plane ich, diese Vorgänge in Zukunft in eine eigene Methode auszulagern.
bool Create(CArrayObj *Description); bool Load(string file_name, float &error, float &undefine, float &forecast, datetime &time, bool common = true); ///< Load method. @param[in] file_name File name to save @param[out] error Average error ///< @param[out] undefine Undefined percent @param[out] Forecast percent ///< @param[out] time Last study time @param[in] common Common flag virtual bool Load(const int file_handle);
Im nächsten Schritt unserer Arbeit gehen wir direkt zur Erstellung von Methoden unserer neuen Klasse über. Die Funktionweise unserer neuen neuronalen Netzklasse CNeuronMLMHSparseAttention entspricht weitgehend der Funktionweise der übergeordneten Klasse CNeuronMLMHAttentionOCL. Daher werden wir versuchen, die abgeleiteten Methoden zu verwenden. Die Hauptunterschiede liegen in der Erzeugung der verringerten Aufmerksamkeit. In diesem Teil wird eine neue interne Variable m_dSparse zum Speichern des Geringfügigkeits-Levels erstellt.
Um die Arbeit nicht durch unnötiges Umschreiben von Methoden zu erschweren, habe ich den Konstruktor und den Destruktor der Klasse leer gelassen. Wir erstellen keine neuen Objekte in der neuen Klasse, und um mit dem Geringfügigkeits-Parameter zu arbeiten, werden wir überladene Geringfügigkeits-Methoden erstellen. Die Möglichkeit, Methoden zu überladen, erlaubt es Ihnen, gleichnamige Methoden für unterschiedliche Funktionen zu verwenden: mit einem Wert in den Parametern, wobei der Wert des Parameters an die Methode übergeben wird; ohne Angabe von Parametern gibt die Methode den zuvor gespeicherten Wert zurück.
class CNeuronMLMHSparseAttention : public CNeuronMLMHAttentionOCL { protected: float m_dSparse; //--- virtual bool AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = true); ///< \brief Multi-heads attention scores method of calling kernel ::MHAttentionScore(). virtual bool AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out); ///< \brief Multi-heads attention out method of calling kernel ::MHAttentionOut(). public: CNeuronMLMHSparseAttention(void) : m_dSparse(0.3f) {}; ~CNeuronMLMHSparseAttention(void) {}; //--- void Sparse(float value) { m_dSparse = value;} float Sparse(void) { return m_dSparse; } virtual int Type(void) const { return defNeuronMLMHSparseAttentionOCL; } ///< Identificatory of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
Vergessen Sie nicht, die virtuelle Identifikationsmethode des Type-Objekts außer Kraft zu setzen.
Was die öffentlichen Methoden betrifft, sollten wir auch die Methoden für die Arbeit mit Dateien überschreiben: Speichern und Laden. Der Algorithmus dieser Methoden ist recht einfach. In diesen Methoden rufen wir zunächst die gleichnamigen Methoden der Elternklasse auf, in der bereits alle Kontrollpunkte definiert und Algorithmen zum Speichern und Laden von geerbten Variablen und Objekten implementiert sind. Wir müssen nur das logische Ergebnis der Ausführung der aufgerufenen Methoden überprüfen. Nach erfolgreicher Ausführung der Methode der übergeordneten Klasse speichern oder lesen wir den Wert des Geringfügigkeits-Parameters, je nach der Funktionweise der laufenden Methode.
bool CNeuronMLMHSparseAttention::Save(const int file_handle) { if(!CNeuronMLMHAttentionOCL::Save(file_handle)) return false; if(FileWriteFloat(file_handle, m_dSparse) < sizeof(float)) return false; //--- return true; }
Wir haben die Überlegungen zu den öffentlichen Methoden für den Betrieb der neuen Klasse abgeschlossen. Die Hauptfunktion der Klasse besteht jedoch darin, den Algorithmus der neuronalen Schicht zu erstellen. Kehren wir also zu den Feed Forward- und Backpropagation-Passagen zurück. Wir haben die OpenCL-Programmkernel modernisiert, um diese Funktionweise zu ermöglichen.
Ich werde ein wenig von der üblichen Struktur abweichen, die wir bei der Beschreibung der Funktionsweise neuronaler Netze zur Erörterung von Methoden verwendet haben. Diesmal werde ich nicht mit Vorwärtsdurchgängen, sondern mit Rückwärtsdurchgängen beginnen. Wir haben keine neuen Kernel für den Backpropagation-Durchgang erstellt. Wir haben nur den bestehenden Kernel geändert, der in der übergeordneten Klasse verwendet wurde. Durch das Ableiten der Funktionsweise der übergeordneten Klasse haben wir auch die Algorithmen für den Aufruf des oben beschriebenen MHAttentionInsideGradients-Kerns geerbt. Das bedeutet, dass wir jetzt einfach die Rückwärtsdurchgangs-Methode von calcInputGradients der übergeordneten Klasse verwenden können, um die Fehlergradienten zu propagieren. An der Funktionweise zur Aktualisierung der trainierten Parameter haben wir keine Änderungen vorgenommen und können auch die Methode updateInputWeights der Elternklasse verwenden.
Kommen wir nun zu den Vorwärtsmethoden. Bei der Konstruktion des Algorithmus des Vorwärtsdurchgangs der übergeordneten Klasse haben wir nicht den gesamten verzweigten Algorithmus im Hauptteil einer einzigen Methode zusammengefasst. Stattdessen haben wir eine strukturierte Dispatch-Methode feedForward erstellt, in der die Methoden der einzelnen Funktionsausführungen nach dem Self-Attention-Algorithmus nacheinander aufgerufen wurden. Dank dieses Ansatzes müssen wir die Feed-Forward-Methode nicht mehr komplett neu schreiben. Wir müssen nur die Methoden umdefinieren, um zwei neue Kernel aufzurufen. Die Methoden sind AttentionScore und AttentionOut.
bool CNeuronMLMHAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false; //--- for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4)); CBufferFloat *qkv = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, qkv, iWindow, 3 * iWindowKey * iHeads, None)) return false; //--- Score calculation CBufferFloat *temp = S_Tensors.At(i * 2); if(IsStopped() || !AttentionScore(qkv, temp, true)) return false; //--- Multi-heads attention calculation CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(qkv, temp, out)) return false; //--- Attention out calculation temp = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false; //--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp)) return false; //--- Feed Forward inputs = temp; temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, out, 4 * iWindow, iWindow, activation)) return false; //--- Sum and normilize out if(IsStopped() || !SumAndNormilize(out, inputs, out)) return false; } //--- return true; }
Um die Regeln der Vererbung zu wahren, erhielten beide Methoden ähnliche Parameter wie die Methoden der Elternklasse. Dies ist äußerst wichtig, da durch die Änderung von Methodenparametern überladene Methoden entstehen würden. Aber wir müssen die Methoden der übergeordneten Klasse außer Kraft setzen. Bei der Methodenüberladung wählt das System je nach den beim Methodenaufruf angegebenen Parametern eine von ihnen aus, während das System bei der Methodenüberschreibung der Vererbungshierarchie folgt und die zuletzt überschriebene Methode verwendet. Daher wird das System nur dann auf die überschriebenen Methoden unserer Klasse zugreifen, wenn wir festlegen, dass die Methoden überschrieben werden, wenn sie von der geerbten feedForward-Methode aufgerufen werden.
Die Methode AttentionScore erhält in ihren Parametern einen Zeiger auf Objekte aus zwei Puffern: einen verketteten Tensor aus Query-, Key- und Value-Entitäten und eine Matrix aus Abhängigkeitskoeffizienten. Darüber hinaus wird das Maskenkennzeichen in den Methodenparametern übergeben. Wir verwenden dieses Kennzeichen nicht; es wird aus den oben genannten Gründen in den Parametern belassen.
Im Methodenkörper wird sofort geprüft, ob die empfangenen Zeiger relevant sind. Wir überprüfen auch die Relevanz des Objekts, das mit dem OpenCL-Kontext arbeitet. Zusätzlich zu den Objektzeigern selbst überprüfen wir das Vorhandensein von erstellten Datenpuffern im OpenCL-Kontext. Erst wenn alle angegebenen Kontrollpunkte erfolgreich durchlaufen wurden, können wir mit der Organisation des Prozesses der Platzierung des Kernels in der Ausführungswarteschlange fortfahren.
Alle von uns erstellten Kernel waren für die Verwendung in einem 2-dimensionalen Problemraum vorgesehen. Nun müssen wir Arrays erstellen, die den Aufgabenbereich global_work_size und den Offset im Aufgabenbereich global_work_offset beschreiben. Die Größe der beiden Arrays muss dem Problemraum entsprechen. Um einen 2-dimensionalen Problemraum zu schaffen, erstellen wir zwei Felder mit jeweils 2 Elementen.
In den Elementen des ersten Feldes geben wir die Gesamtzahl der Elemente der analysierten Sequenz und die Anzahl der Aufmerksamkeitsköpfe an. Die Position eines Elements in einem Array gibt eine Dimension an. Sein Wert gibt die Anzahl der Threads an. So erhält jedes Element der Sequenz für jeden Aufmerksamkeitskopf einen eigenen Thread zur Durchführung von Operationen. Im Allgemeinen werden die Operationen auf allen Elementen der Sequenz gleichzeitig (soweit technisch möglich) in parallelen Threads durchgeführt.
Wir füllen die Elemente des zweiten Arrays mit Nullwerten, da wir keinen Offset im Aufgabenbereich benötigen.
bool CNeuronMLMHSparseAttention::AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = true) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(qkv) == POINTER_INVALID || CheckPointer(scores) == POINTER_INVALID) return false; //--- if(qkv.GetIndex() < 0) return false; if(scores.GetIndex() < 0) return false; //--- uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = iUnits; global_work_size[1] = iHeads; OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionScore, def_k_mhas_qkv, qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionScore, def_k_mhas_score, scores.GetIndex()); OpenCL.SetArgument(def_k_MHSparseAttentionScore, def_k_mhas_dimension, (int)iWindowKey); OpenCL.SetArgument(def_k_MHSparseAttentionScore, def_k_mhas_sparse, (float)m_dSparse); if(!OpenCL.Execute(def_k_MHSparseAttentionScore, 2, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %s", __FUNCSIG__, error); return false; } //--- return true; }
Der nächste Schritt besteht darin, die Parameter an den Kernel zu übergeben. Wir tun dies mit den Methoden SetArgumentBuffer und SetArgument. Der erste wird zur Übergabe von Zeigern auf Datenpuffer verwendet. Der zweite wird für die Übermittlung diskreter Werte verwendet. In den Methodenparametern geben wir den Kernel-Identifikator, die Seriennummer des übergebenen Parameters (entspricht der Reihenfolge der Kernel-Parameter im OpenCL-Programm beginnend mit 0) und den übergebenen Wert an.
Hier sollten Sie auf die Art der übergebenen Werte und die im Kernel angegebene Art der Parameter achten. Wenn die Typen nicht übereinstimmen, kann ein Fehler bei der Kernelausführung auftreten.
Sobald die Vorbereitungsarbeiten abgeschlossen sind, rufen wir die Execute-Methode auf, um den Kernel an die Ausführungswarteschlange zu senden. In den Methodenparametern geben wir den Kernel-Identifikator, die Dimension des Aufgabenraums und die zuvor erstellten Aufgabenraumbeschreibungsfelder an.
Wir überprüfen auch das Ergebnis der Ausführung der Kernel-Warteschlangenmethode. Wenn beim Einreihen des Kernels in die Warteschlange ein Fehler auftritt, fordern Sie Informationen über den Fehler an und zeigen Sie diese im Terminalprotokoll an.
Wenn der Kernel erfolgreich in die Ausführungswarteschlange aufgenommen wurde, schließen wir die Methode mit dem Ergebnis ‚true‘ ab.
Wir verwenden einen ähnlichen Algorithmus in der Methode AttentionOut, um den zweiten Kernel aufzurufen.
bool CNeuronMLMHSparseAttention::AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(qkv) == POINTER_INVALID || CheckPointer(scores) == POINTER_INVALID || CheckPointer(out) == POINTER_INVALID) return false; uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = iUnits; global_work_size[1] = iHeads; if(qkv.GetIndex() < 0) return false; if(scores.GetIndex() < 0) return false; if(out.GetIndex() < 0) return false; //--- OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_qkv, qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_score, scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_out, out.GetIndex()); OpenCL.SetArgument(def_k_MHSparseAttentionOut, def_k_mhao_dimension, (int)iWindowKey); if(!OpenCL.Execute(def_k_MHSparseAttentionOut, 2, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %s", __FUNCSIG__, error); return false; } //--- return true; }
Damit ist unsere Arbeit mit der neuen Klasse der neuronalen Netze abgeschlossen. Aber es bleibt noch ein Punkt übrig. Wir müssen die Verarbeitung unserer neuen Klasse zu den Versandmethoden hinzufügen, die den Betrieb des Modells implementieren.
Zunächst fügen wir in der Methode CNet::Create einen Block zur Erstellung einer neuen Art von neuronaler Schicht hinzu.
case defNeuronMLMHSparseAttentionOCL: neuron_sparseattention = new CNeuronMLMHSparseAttention(); if(CheckPointer(neuron_sparseattention) == POINTER_INVALID) { delete temp; return false; } if(!neuron_sparseattention.Init(outputs, 0, opencl, desc.window, desc.window_out, desc.step, desc.count, desc.layers, desc.optimization, desc.batch)) { delete neuron_sparseattention; delete temp; return false; } neuron_sparseattention.SetActivationFunction(desc.activation); neuron_sparseattention.Sparse(desc.probability); if(!temp.Add(neuron_sparseattention)) { delete neuron_mlattention_ocl; delete temp; return false; } neuron_sparseattention = NULL; break;
Wir fügen der Methode CLayer::CreateElement einen neuen Ebenentyp hinzu.
case defNeuronMLMHSparseAttentionOCL: if(CheckPointer(OpenCL) == POINTER_INVALID) return false; temp_mlat_ocl = new CNeuronMLMHSparseAttention(); if(CheckPointer(temp_mlat_ocl) == POINTER_INVALID) result = false; if(temp_mlat_ocl.Init(iOutputs, index, OpenCL, 1, 1, 1, 1, 0, ADAM, 1)) { m_data[index] = temp_mlat_ocl; return true; } break;
Den neuen Typ fügen wir auch in die Feed Forward Dispatch-Methode der Basisklasse des neuronalen Netzes ein.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject) == POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp = NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronProofOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronMLMHSparseAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: case defNeuronVAEOCL: case defNeuronLSTMOCL: case defNeuronSoftMaxOCL: temp = SourceObject; return feedForward(temp); break; } //--- return false; }
Wir wiederholen den Vorgang in der entsprechenden Rückverfolgungsmethode CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject).
case defNeuronMLMHAttentionOCL: case defNeuronMLMHSparseAttentionOCL: mlat = TargetObject; if(!bTrain && !mlat.TrainMode()) return true; temp = GetPointer(this); return mlat.calcInputGradients(temp);
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
3. Tests
Nachdem wir die Arbeit an der neuen neuronalen Schichtklasse abgeschlossen haben, können wir mit dem Testen des konstruierten Algorithmus im Handelsstrategie-Tester der MetaTrader 5-Plattform fortfahren. Der Strategy Tester ermöglicht das Testen von handelnden Expert Advisors und Indikatoren anhand historischer Daten. Um die Funktionsweise des konstruierten Algorithmus zu testen, werden wir einen kleinen Handels-EA erstellen, der das Modell direkt beim Durchlaufen der historischen Daten trainiert. Wir haben bereits ähnliche EAs erstellt, als wir die zuvor besprochenen Algorithmen getestet haben. Dieses Mal werden wir den EA aus dem vorherigen Artikel als Grundlage verwenden. In diesem EA ersetzen wir die mehrköpfige neuronale Aufmerksamkeitsschicht in der Modellarchitektur des EA durch eine neu geschaffene verringerte Aufmerksamkeitsschicht.
Im vorigen Artikel haben wir ein relationales Verstärkungslernmodell getestet, das einen vollständig parametrisierten Quantilfunktionsalgorithmus mit einem intrinsischen Neugierblock verwendet. Um ein solches Modell zu implementieren, haben wir eine Kombination aus 3 Modellen erstellt: Modell, vorwärts und rückwärts. Im ersten Modell haben wir den Aufmerksamkeitsblock verwendet. Wir werden diesen Block also ändern. Die Architektur der beiden anderen Modelle blieb unverändert.
Die Architektur der Modelle wird mit der Funktion CreateDescriptions beschrieben. Um das Modell zu vereinfachen, habe ich beschlossen, die Verwendung rekursiver LSTM-Blöcke zu streichen. Sie wurden durch vollständig verbundene Schichten ersetzt. Das Trainingsmodell hat also die folgende Architektur.
Für die Modelleingabe wurde eine Schicht von Ausgangsdaten mit 12 Elementen zur Beschreibung jedes Balkens der analysierten Historie und 9 Elementen zur Beschreibung des aktuellen Kontostands erstellt.
//--- Model Description.Clear(); CLayerDescription *descr; //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (int)(HistoryBars * 12 + 9); descr.window = 0; descr.activation = None; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; }
Darauf folgt eine Daten-Normalisierungsschicht.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; }
Darauf folgen 2 aufeinanderfolgende Blöcke von Faltungsschichten und vollständig verbundenen Schichten.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = prev_count - 2; descr.window = 3; descr.step = 1; descr.window_out = 6; descr.activation = LReLU; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 100; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 50; descr.window = 2; descr.step = 2; descr.window_out = 4; descr.activation = LReLU; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 100; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; }
Die komprimierten Daten werden durch den Aufmerksamkeitsblock analysiert. Hier verwenden wir die neue Schicht (layer) der verringerten Aufmerksamkeit. Wir teilen die gesamte Sequenz der komprimierten Daten in 20 Blöcke zu je 5 Elementen auf. Jeder Block steht für ein Element der zu analysierenden Sequenz. Zur Analyse der Daten werden 4 Aufmerksamkeitsköpfe verwendet, wobei in jedem Aufmerksamkeitskopf 30 % der wichtigsten Sequenzelemente ausgewählt werden. Die Analyse wird in 2 aufeinanderfolgenden Schichten mit ähnlichen Parametern durchgeführt. Dies sollte im Parameter „layers“ angegeben werden.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLMHSparseAttentionOCL; descr.count = 20; descr.window = 5; descr.step = 4; descr.window_out = 8; descr.layers = 2; descr.probability = 0.3f; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; }
Der Expert Advisor trifft die Entscheidung, ob ein Handel in einem Block einer vollständig parametrisierten Quantil-Funktion ausgeführt werden soll. Der EA kann sich für eine von 4 Aktionen entscheiden:
- Kaufen (buy)
- Verkaufen (sell)
- Alle Positionen schließen
- Kein Handel
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFQF; descr.count = 4; descr.window_out = 32; descr.optimization = ADAM; if(!Description.Add(descr)) { delete descr; return false; }
Der vollständige EA-Code ist im Anhang enthalten: SparseRL-learning.mq5.
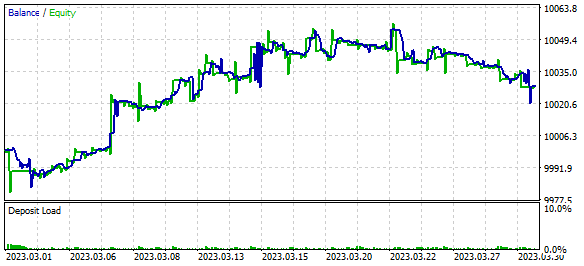
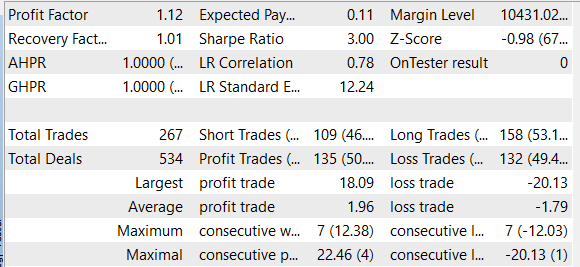
Wir haben das Modell trainiert und den EA mit historischen EURUSD H1-Daten für März 2023 getestet. Während des Lernprozesses zeigte der EA während der Testphase Gewinne. Der Gewinn wurde jedoch erzielt, weil der Umfang der durchschnittlichen Ergebnisse der Positionen mit Gewinn größer war als der mit Verlust. Die Anzahl der Gewinner und Verlierer war jedoch ungefähr gleich. Infolgedessen lag der Gewinnfaktor (profit factor) bei 1,12 und der Erholungsfaktor (recovery factor) bei 1,01.
Schlussfolgerung
In diesem Artikel haben wir den Sparse Attention-Mechanismus untersucht und seinen Algorithmus in unsere Klassenbibliothek aufgenommen, um ihn anschließend an historischen Daten zu testen. Als Ergebnis der Modelltests konnten wir einige Gewinne erzielen, was auf die potenzielle Möglichkeit hinweist, eine solche Architektur für den Aufbau von Handelslösungen zu nutzen. Es sei jedoch darauf hingewiesen, dass das in diesem Artikel vorgestellte Modell nur zu Informations- und Testzwecken dient.
Um dieses Modell unter realen Handelsbedingungen zu verwenden, müssen Sie eine genauere Analyse seiner Wirksamkeit und seiner Widerstandsfähigkeit gegenüber Marktschwankungen durchführen. Außerdem ist eine sorgfältigere Abstimmung der Hyperparameter des Modells erforderlich, um optimale Ergebnisse zu erzielen.
Sie sollten immer bedenken, dass die Verwendung eines Modells für den Finanzmarkthandel immer mit einem Verlustrisiko verbunden ist. Bevor Sie also ein Modell für den realen Handel verwenden, müssen Sie sein Funktionsprinzip sorgfältig studieren und die möglichen Risiken abschätzen.
Trotzdem kann der Sparse Attention-Mechanismus ein nützliches Instrument für die Erstellung von Handelsmodellen sein.
Referenzen
- Generating Long Sequences with Sparse Transformers
- Attention Is All You Need
- Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen
- Neuronale Netze leicht gemacht (Teil 10): Multi-Head Aufmerksamkeit
- Neuronale Netze leicht gemacht (Teil 11): Ein Blick auf GPT
- Neuronale Netze leicht gemacht (Teil 35): Modul für intrinsische Neugierde
- Neuronale Netze leicht gemacht (Teil 36): Relationales Verstärkungslernen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | SparseRL-learning.mq5 | EA | Ein Expert Advisor zum Trainieren des Modells |
| 2 | ICM.mqh | Klassenbibliothek | Modellorganisation Klassenbibliothek |
| 3 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 4 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/12428
- Freie Handelsapplikationen
- Freie Forex-VPS für 24 Stunden
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.