Desarrollo de un sistema de repetición — Simulación de mercado (Parte 14): Nacimiento del SIMULADOR (IV)

Introducción

En el artículo anterior, "Desarrollo de un sistema de repetición — Simulación de mercado (Parte 13): Nacimiento del SIMULADOR (III), mostré los cambios realizados en el archivo de servicio para promover una mejor presentación de los ticks y su manejo. A pesar de todo, el enfoque principal del artículo anterior fue mostrar cómo tú puedes hacerlo y dónde necesitas modificar y agregar código para obtener datos del servicio. Esto te permitiría transportar esos datos a otro lugar, que en este caso es un archivo. Teniendo este archivo en tus manos, podrías utilizar un programa, en este caso mostré cómo usar EXCEL, para analizar los datos que el simulador generará.

Este tipo de tarea, aunque parezca trivial, es de suma importancia para lo que vamos a hacer en este artículo. Sin saber cómo analizar los datos que el simulador generará, no podrás comprender lo que será necesario implementar; pero, sobre todo, no comprenderás por qué se está implementando de la manera que mostraré. Además del tema principal del artículo anterior, también se explicaron algunos puntos que debían modificarse en el código para lograr que la barra se creara en aproximadamente 1 minuto, con una buena precisión, para que las cosas se acerquen mucho a la realidad. Sin embargo, a pesar de todo esto, para comprender lo que vamos a hacer en este artículo, es necesario entender una cosa. Y dado que el artículo anterior ya tenía mucha información, he decidido explicar aquí un último detalle que se puede ver en el código adjunto.

Intento de un paseo aleatorio libre

La versión más básica del procedimiento que intentará crear un paseo aleatorio libre se puede ver a continuación.

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long il0, max;
                                double v0, v1;
                                int p0;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;                           
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;
                                for (int c0 = 1; c0 < max; c0++)
                                        tick[c0].last = macroRandomLimits(rate.low, rate.high);                                 
                                il0 = (long)(max * (0.3));
                                tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                tick[macroRandomLimits(max - il0, max)].last = rate.high;                                         
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
                        }
                        
#undef macroRandomLimits

Es extremadamente importante comprender este código anterior para entender lo que haremos a partir de ahora. Entonces, si ejecutas exactamente este código, obtendrás un gráfico muy confuso. Sin embargo, es importante entender cómo funciona esta rutina más básica para que puedas comprender cómo funcionarán las rutinas más complicadas. Entonces, comencemos con la definición de la macro. Pregunta: ¿Qué hace esta macro? Puedes estar mirando y pensando: ¿Qué locura es esta? ¿Realmente necesitamos algo tan extravagante? Bueno, la respuesta a eso es un SÍ y un NO.

SÍ, porque necesitamos que el valor aleatorio se genere dentro de un rango muy específico. Para esto, necesitamos establecer algún tipo de límite. Y NO, porque para generar el RANDOM WALK, no necesitaremos este cálculo en sí. Pero nuevamente, debes entender cómo funciona este sistema más simple para comprender los otros que serán más elaborados.

Entonces, cuando realizamos una operación AND, limitaremos el valor a un rango. Este es el primer punto. Si dividimos este valor por el límite superior del rango, obtendremos un valor que oscilará entre 0 y 1. Luego, multiplicaremos este valor, que estará entre 0 y 1, por la diferencia entre el límite superior e inferior. De esta manera, obtendremos un valor que oscilará entre 0 y un valor máximo que será nuestro rango. Ahora, si sumamos este rango al valor mínimo, obtendremos el valor que realmente queremos y debemos usar. Así que no necesitaremos preocuparnos por hacer ninguna otra prueba, la propia macro garantizará que el valor esté dentro de los límites. ¿Captaste la idea detrás de esta macro loca? Es pura y simple matemática, nada más que eso.

Luego, pasemos al primero de los cuatro bucles FOR que tenemos dentro de la rutina. Antes de entrar realmente en el bucle, tenemos algunos cálculos simples que nos ayudarán en el resto de la rutina. Lo primero es saber cuántos ticks simularemos en realidad. Luego, necesitaremos saber cuánto tiempo tendrá cada uno de los ticks. O mejor dicho, en qué momento deberán aparecer. Para no complicar las cosas, utilizaremos un tiempo constante entre ellos. Ahora podemos entrar en el bucle y distribuir los ticks dentro del rango de la barra de 1 minuto. En algunos casos, los ticks estarán más separados y, en otros casos, estarán más cerca unos de otros. Esto realmente no importa en este momento. Lo que necesitamos y queremos es lo que realmente importa. Y eso será que cada uno sea y deba ser único. Esto se logra colocándolos en puntos diferentes en el tiempo.

También puedes notar que estoy estableciendo que cada tick simulado inicialmente tendrá un valor mínimo de volumen. Esto también es importante para el próximo paso. Entonces, entramos en el próximo bucle. Aquí es donde las cosas comienzan a ponerse interesantes, ya que lo primero que hacemos es definir cuál será el precio de apertura y cierre de la barra de 1 minuto. Sin embargo, lo verdaderamente interesante es lo que está sucediendo dentro del bucle. Observa que restaremos el volumen total del número de ticks que se utilizarán. Con esto, obtenemos un valor que es el volumen que aún no se ha distribuido. Podríamos colocar este valor directamente en el último tick o en algún otro tick. Sin embargo, hacerlo crearía un movimiento brusco en el volumen, lo cual no suele suceder con frecuencia en el mercado real. Por lo tanto, necesitamos otro método para distribuir los ticks restantes de manera que el volumen final sea el que se expresa en el valor de la barra de 1 minuto. Para crear esta distribución de la manera más suave y al mismo tiempo aleatoria, utilizaremos nuestra macro. Observa que en cada llamada, la macro generará un valor que estará dentro de los límites definidos. Y es precisamente en este momento cuando el valor presente en el volumen se incrementará en 1. Es decir, el volumen total se distribuirá de manera aleatoria y sin sobresaltos, dando la impresión de que son datos similares a los de un mercado real.

Para finalizar, veamos los dos últimos bucles. El primer bucle es el que creará la aleatoriedad en nuestro sistema de ticks. Observa que no necesitamos hacer ningún esfuerzo. Todo lo que hacemos es decirle al sistema cuál es el precio mínimo y máximo a utilizar. De esta manera, cada uno de los ticks tendrá un precio elegido al azar. Ten en cuenta que estamos utilizando la macro para hacer este proceso de elección por nosotros. Después de que esto se haya hecho, debemos asegurarnos de que tanto el punto de máximo valor como el punto de menor valor estén presentes. Esto se debe a que pueden no haberse creado durante la generación aleatoria de valores. Pero la posición en la que se encontrarán estos puntos también se elegirá al azar.

En cuanto al último bucle, simplemente transferirá los valores al sistema de ticks para que se utilicen como si fueran ticks reales. El resultado se puede ver y entender si guardas los datos de salida en un archivo y luego utilizas los datos obtenidos como datos para manipular en un gráfico. Normalmente hacemos esto en algún programa como Excel. Pero también se puede hacer directamente en MetaTrader 5, utilizando algún tipo de activo personalizado. Pero no te preocupes por estos detalles en este momento. Lo importante es que entiendas que la simulación realmente ocurrirá como se espera.

Basado en la explicación anterior que comenzamos en el artículo anterior, puedes notar que he empezado a dar prioridad a una aleatorización del movimiento. A diferencia de lo que se puede ver en los otros artículos, donde se utilizaba un método para crear una simulación muy parecida a la encontrada en el simulador de estrategias, utilizando el movimiento de zigzag, muy similar a lo que se muestra en la figura a continuación:

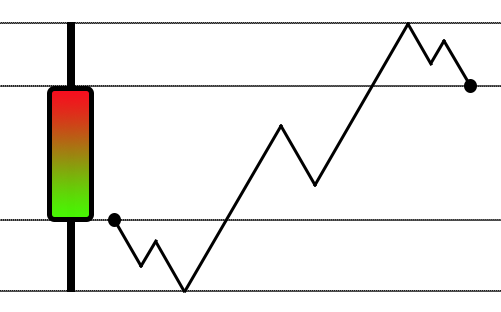
Aunque es una excelente idea para ser utilizada en el simulador de estrategias, este tipo de enfoque no es muy adecuado para un sistema de repetición/simulación. Se requiere un enfoque diferente, un poco más creativo y al mismo tiempo más complejo. De esta forma, nació el sistema que acabo de explicar. Ahí comenzamos a aleatorizar de manera bastante sencilla los movimientos dentro de la barra de 1 minuto. Pero ese tipo de enfoque no es muy adecuado cuando la intención es tener un estilo de movimiento muy similar al de un objeto suspendido en un líquido, ya que había saltos entre los puntos. Para ayudarte a comprender cómo se hace esto, es importante que sepas cómo convertir una serie de datos en algo visible en un gráfico. La forma más simple de hacerlo es utilizando EXCEL para la conversión. Nuevamente, es importante que sepas cómo hacerlo.

En el artículo anterior, "Desarrollo de un sistema de repetición — Simulación de mercado (Parte 13): Nacimiento del SIMULADOR (III)", esto se explicó en el vídeo. Es de suma importancia que sepas cómo hacerlo si realmente deseas entender lo que ocurrirá en este artículo. Esto se debe a que aquí crearemos una simulación de movimiento de manera que parecerá un RANDOM WALK. Al ver los gráficos generados por el simulador, notarás de inmediato que el movimiento se asemeja mucho al movimiento visto durante la fase de negociación de un activo. No incluiré fórmulas matemáticas ni cosas por el estilo en este artículo. No veo ningún beneficio en traer este tipo de enfoque. Lo que realmente interesa a todos es el código en sí y lo que produce. Las fórmulas matemáticas involucradas no agregan nada en absoluto para muchos y tampoco aportan ningún conocimiento, ya que muchos no entenderán las cuestiones abstractas involucradas. Por lo tanto, esto complicaría más que explicaría. Pero con toda seguridad, todos entenderán los resultados obtenidos.

Lo que se verá en este artículo es una forma lo más simple posible de transformar la Figura 01 en la Figura 02:                   

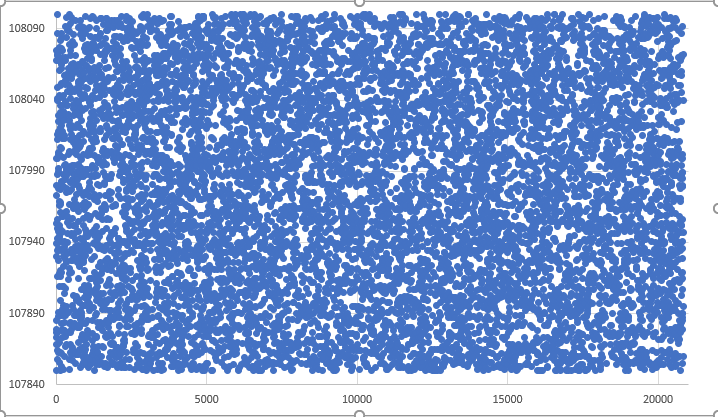
Figura 01 - Movimiento aleatorio ejecutado en saltos

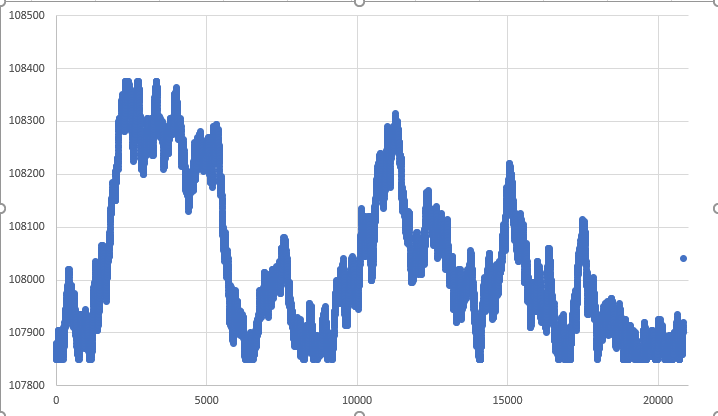
Figura 02 - Movimiento aleatorio realizado en pasos

Pero utilizando la misma base de datos, que en este caso se muestra a continuación:

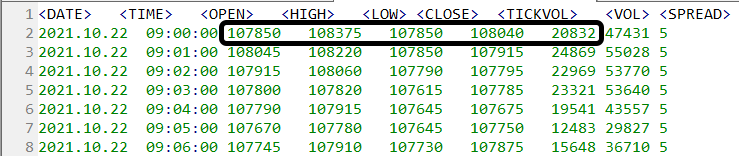
Figura 03 - Base de datos utilizada en ambos movimientos

Sin embargo, y nuevamente, repetiré y enfatizaré la palabra PERO. Hay cuestiones que, a diferencia de un sistema completamente aleatorio, necesitaremos corregir. Sin embargo, incluso así, no tendremos de inmediato un sistema verdaderamente adecuado en más del 99% de las ocasiones, ya que este 1% restante se debe a alguna casualidad que hace que el modelado sea perfecto. Será algo poco frecuente. Por lo tanto, necesitaremos algunos trucos para solucionar todos los otros casos, es decir, el 99%.

Pero basta de rodeos, veamos cómo funciona realmente el sistema. Pero antes de eso, si no has leído el artículo anterior "Desarrollo de un sistema de repetición — Simulación de mercado ( Parte 13 ): Nacimiento del SIMULADOR (III)", te sugiero encarecidamente que te detengas y leas primero el artículo anterior antes de continuar con este. La razón es que aquí solo me enfocaré en los cambios necesarios y cómo deben implementarse. No repetiré las explicaciones que se dieron en el artículo anterior. Y comprender el contenido allí presente será importante para entender este. Sobre todo la parte relacionada con la transformación de datos en un gráfico, esto dentro de Excel.

Dado este aviso, pasemos al tema de la implementación.

Aplicación de un RANDOM WALK de movimiento totalmente libre

Todo lo que necesitamos hacer para transformar un movimiento aleatorio de saltos en un movimiento aleatorio de pasos es cambiar la forma en que funciona la función de simulación. Para hacer esto, veamos el código de la misma:

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long il0, max;
                                double v0, v1;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;
                                for (int c0 = 1; c0 < max; c0++)
                                        tick[c0].last = macroRandomLimits(rate.low, rate.high);
                                        tick[c0].last = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1));
                                il0 = (long)(max * (0.3));
                                tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                tick[macroRandomLimits(max - il0, max)].last = rate.high;
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
#undef macroRandomLimits
                        }                       

Observa que cambiamos solo y exclusivamente la forma en que la función trabaja. Pero aún así, mantuvimos la misma carga. Es decir, utilizaremos la misma cantidad de ticks. Sin embargo, presta atención a algo muy específico en la parte destacada. Ahora, presta mucha atención al siguiente hecho: El código que está BORRADO debe ser eliminado y en su lugar entra el código destacado. Haciendo solo este cambio, ya seremos capaces de crear un RANDOM WALK. Pero no es un movimiento adecuado. Aún no. Porque aunque en algún raro momento ocurra que el movimiento se mantenga dentro del rango de la barra de 1 minuto, es decir, respete el máximo y el mínimo y quede contenido dentro de esta amplitud, no tenemos certeza ni control sobre esto en el código anterior. Esto se puede notar al ejecutarlo y verificar el gráfico obtenido.

Si estás utilizando los archivos adjuntos y no cambias el archivo de configuración, hará que el servicio de repetición/simulador solo funcione en la primera barra. Y la barra que se utilizará es precisamente la que se destaca en la imagen a continuación:

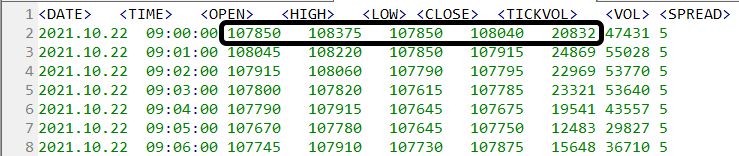
Observa que los límites son: LÍMITE SUPERIOR => 108375 y LÍMITE INFERIOR => 107850. Y estos no son los límites que verás al observar el gráfico. Incluso con una mirada rápida, notarás que estos límites no se están respetando. Para ilustrar mejor, mira la imagen del gráfico de datos de una de las ejecuciones. Esto se puede ver a continuación.

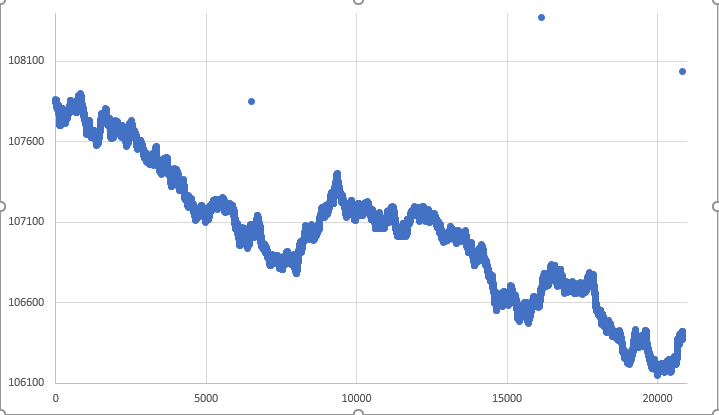
Figura 04 - Representación del RANDOM WALK totalmente libre

Inmediatamente notarás que el límite inferior está lejos de ser respetado. Nuevamente, puede ocurrir en algún momento muy, pero muy específico, que los límites se respeten. Existe otro problema con respecto a los puntos aislados que se pueden ver en el gráfico anterior. Pero vayamos con calma. Estos puntos representan otro problema que tendremos que resolver. Sin embargo, nuestro enfoque en este primer momento es realmente el problema de los límites. A diferencia de lo que podría ser aceptable cuando estamos creando simulaciones de movimiento, aquí esa aceptación no estará presente. El motivo es que estamos realizando simulaciones basadas en algún tipo de dato previamente obtenido y debemos respetar lo que se nos informa.

Resolver este problema de los límites nos obliga a convertir un sistema libre en un sistema limitado. Aunque muchos puedan fruncir el ceño ante este enfoque, no tenemos otra opción más que realmente crear algún tipo de prueba para que los límites se respeten a toda costa. Por lo tanto, es importante que hayas leído el artículo anterior. Debes entender cómo utilizar EXCEL o cualquier otro programa para analizar el gráfico generado por el sistema de simulación. No confíes únicamente en mirar los datos y pensar que están correctos. Realmente debes observarlos en un gráfico.

A diferencia de lo que ocurre cuando tenemos un sistema completamente aleatorio basado en saltos, como se muestra en la Figura 01, donde usar el sistema de trazado de gráficos de MetaTrader 5 es completamente inviable, no sucede lo mismo cuando obtenemos lo que se ve en la Figura 02 o incluso en la Figura 04. Aunque en ambos casos tendremos el problema de los puntos aislados en el gráfico, lo que generará una barra extraña. Sin embargo, si no te apetece llevar los datos de la simulación al EXCEL, puedes realizar algunos cambios en el código para que cada uno de los ticks se trace directamente en el gráfico de MetaTrader 5. Aunque esto hará que el gráfico sea más complicado de entender debido a la cantidad de información que contendrá. Recuerda: Deberás colocar tick a tick en el gráfico, no las barras. Si no sabes cómo hacerlo, consulta este artículo: "Desarrollo de un EA de trading desde cero (Parte 13): Times And Trade (II)", ya que en él explico cómo trazar los ticks que estamos generando aquí en el simulador. Aunque Times And Trade se enfoca en mirar los ticks reales de un activo, nada te impide usarlo para ver los ticks generados aquí en el simulador. Todo se trata de adaptar el código mostrado para Times And Trade.

Esto no es una tarea muy compleja, pero implicará cambios que luego deberán deshacerse. Por lo tanto, no mostraré cómo hacerlo. El objetivo aquí es mostrar de manera muy simple cómo hacer que el sistema genere un movimiento de manera que tengamos una simulación de un posible movimiento dentro de la barra de 1 minuto, pero de forma continua y no a saltos. Creo que muchos de los que están leyendo estos artículos no tienen un gran conocimiento sobre cómo programar estas cosas utilizando MQL5. Cambiar el enfoque solo por satisfacción personal está completamente fuera del alcance de este o cualquier otro artículo de esta secuencia. Por lo tanto, continuemos con nuestro trabajo de esta manera. Ahora agreguemos algunas cosas al código para que cumpla con los límites impuestos, que están determinados por la información contenida en la barra de 1 minuto destacada en la Figura 03.

Aplicación de un RANDOM WALK de movimiento limitado

Basándonos en lo que se vio en el tema anterior, podemos ver fácilmente qué y dónde debemos actualizar. Los cambios se pueden ver en el código a continuación:

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long    il0, max;
                                double  v0, v1;
                                bool    bLowOk, bHighOk;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;
                                bLowOk = bHighOk = false;
                                for (int c0 = 1; c0 < max; c0++)
                                {                               
                                        v0 = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1));
                                        if (v0 <= rate.high)
                                                v0 = tick[c0].last = (v0 >= rate.low ? v0 : tick[c0 - 1].last + m_PointsPerTick);
                                        else
                                                v0 = tick[c0].last = tick[c0 - 1].last - m_PointsPerTick;
                                        bLowOk = (v0 == rate.low ? true : bLowOk);
                                        bHighOk = (v0 == rate.high ? true : bHighOk);
                                }                                       
                                il0 = (long)(max * (0.3));
                                if (!bLowOk) tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                if (!bHighOk) tick[macroRandomLimits(max - il0, max)].last = rate.high;
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
#undef macroRandomLimits
                        }                       

Puede parecerte que los cambios no están ocurriendo o que estás un poco confundido con todas estas marcas. Pero ten en cuenta que hemos añadido dos nuevas variables para ayudarnos a controlar las cosas un poco mejor. Estas se inicializan de manera que si las posiciones que representan no se acceden adecuadamente, forzosamente tendremos que colocar esos puntos en el gráfico. Y estos puntos se eligen al azar. Pero las pruebas se realizan dentro del sistema de búsqueda y análisis de límites. Así que podemos centrarnos solo y exclusivamente en una cosa: mantener el RANDOM WALK dentro de los límites establecidos previamente por las barras de 1 minuto. Lo primero que probaremos es si el límite superior ha sido violado y irrespetado. Si esto ha sucedido, volveremos a poner inmediatamente el movimiento dentro de los límites. Si se ha respetado, realizaremos otra prueba en la que esta vez verificaremos si se ha irrespetado el límite inferior. Si es así, haremos que el movimiento regrese inmediatamente dentro de los límites. De lo contrario, el valor será aceptado.

Observa que no hemos cambiado muchas cosas en el código. Sin embargo, los resultados sí han experimentado cambios significativos. Mira lo que ocurrió en una de las ejecuciones.

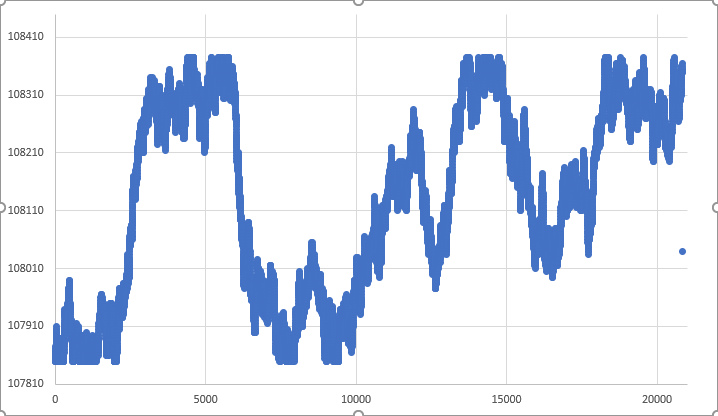
Figura 05 - Movimiento RANDOM WALK dentro de los límites

Es cierto que fue pura suerte que el movimiento haya cubierto todos los puntos aislados. Pero aún así, tenemos un punto suelto en el gráfico. Este punto representa el tick de cierre de la barra de 1 minuto. De hecho, es bastante difícil alcanzarlo de manera precisa dada la naturaleza del movimiento aleatorio y la forma en que lo estamos haciendo. Pero aparte de eso, puedes notar que, a diferencia de la Figura 04 donde los límites no se respetaron, en la Figura 05, sí se respetaron y toda la barra de 1 minuto estará contenida dentro de los límites establecidos previamente. Entonces, el movimiento está casi perfecto. Y digo "casi" porque el resultado de la Figura 05 fue pura suerte. En la mayoría de los casos, obtendrás un resultado similar al de la Figura 06 que se muestra a continuación.

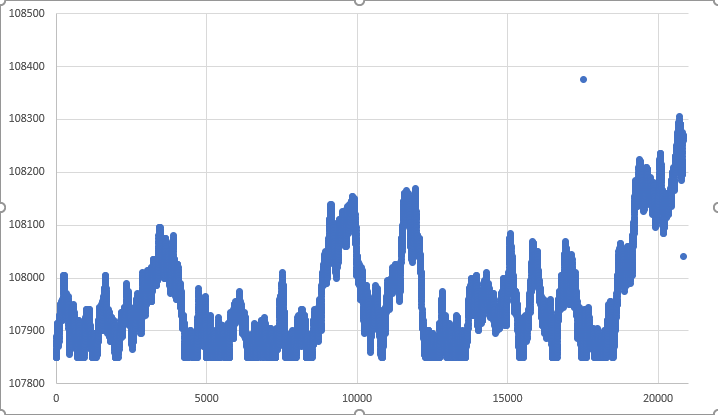
Figura 06 - Gráfico típico del movimiento dentro de los límites

Ten en cuenta que también en la Figura 06, el punto de cierre no se alcanzó en el momento deseado por el sistema de movimiento aleatorio. Sin embargo, en casos extremadamente raros, podrías obtener un resultado como el de la Figura 07. Aquí puedes notar que el punto de cierre fue alcanzado por el movimiento aleatorio.

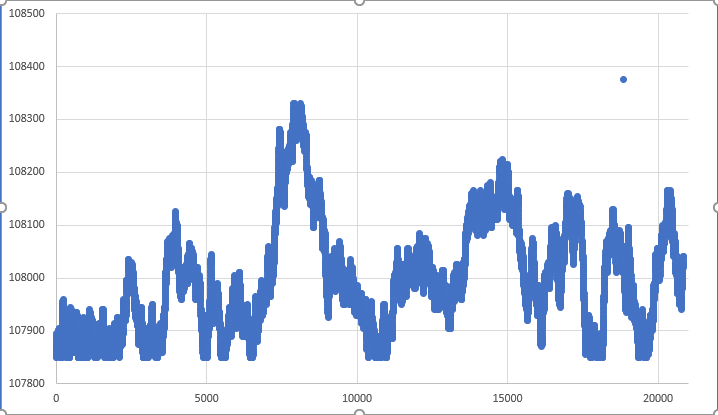
Figura 07 - Movimiento RARO donde se alcanzó el punto de cierre.

Pero este tipo de movimiento es tan raro que no podemos contar realmente con él. En la mayoría de las ocasiones, el tick anterior al cierre estará lejos del punto de cierre. Esto causará un movimiento abrupto en el gráfico del activo de repetición/simulación que está siendo trazado por MetaTrader 5. Si no te importa este tipo de efecto, perfecto, el sistema ya puede considerarse adecuado para que lo utilices. Pero debes notar otra cosa. En varios momentos, y esto no es tan raro, los puntos máximos o mínimos no son realmente visitados. Esto significa que en un segundo punto, o tercero dependiendo del caso, tendremos otro movimiento brusco por parte del sistema de trazado del activo. De alguna manera, esto no es un problema muy grande, al menos la mayoría de las veces. Ya que en un mercado real, de hecho, tenemos tales movimientos en algunos momentos. Pero si aún así, tu deseo es crear un sistema donde estos movimientos no sean tan frecuentes, debemos adoptar otra medida. En otras palabras, tendremos que hacer más cambios en el sistema de simulación. Sin embargo, estos cambios no vendrán sin dificultades. Por el contrario, su implementación será un proceso complicado y difícil de entender para algunos. Además, si deseas tener un gráfico muy similar al que se ve en la Figura 07, necesitaremos realizar estos cambios.

Creo que muchos ya están bastante satisfechos con los resultados presentados en esta versión. Sin embargo, aún podemos mejorar todo esto. Para aquellos que creen que esto es suficiente, es posible que el próximo artículo no les parezca necesario. Pero para aquellos que desean ser perfeccionistas, tengo una última propuesta para trabajar. Esto generará el RANDOM WALK donde no habrá puntos sueltos. Así, todos los puntos serán visitados con seguridad. Pero por hoy, es suficiente. Te dejaré asimilar el conocimiento contenido en este artículo. Deberás probar el sistema varias veces con diferentes tipos de activos. Solo entonces sabrás realmente si utilizando el concepto de RANDOM WALK limitado, los movimientos posibles dentro de una barra de 1 minuto son adecuados y representan una posible realidad del mercado que deseas utilizar.

Consideraciones finales

Sin prácticamente ninguna presentación de fórmulas matemáticas complejas o hablando de una manera que nadie realmente entendería, creo que te he transmitido, querido lector, un concepto bastante interesante y presente en el mercado. Se trata del llamado RANDOM WALK (paseo aleatorio). El sistema presentado en este artículo muestra cuánto podemos avanzar sin realmente entender conceptos complejos. Aunque, por supuesto, siempre es bueno adquirir conocimiento. Pero, ¿por qué complicarlo si podemos explicar las cosas de una manera bastante simple y agradable? ¿No es cierto?

En el archivo adjunto, tendrás el sistema en su estado actual de desarrollo. Creo que muchos de ustedes deben estar ansiosos por saber cuándo empezaremos realmente a tener un sistema de órdenes en nuestra repetición/simulador. Pero no se preocupen, pronto comenzaremos a agregar el sistema de órdenes, pero antes de hacerlo, necesitamos hacer una serie de otras cosas. Esto se debe a que el sistema de órdenes será un problema bastante interesante de resolver. Pero primero debemos terminar de implementar el servicio de repetición/simulador, que ya parece estar casi listo. Solo faltan unos pocos detalles por agregar. Después de eso, podremos comenzar a desarrollar el sistema de órdenes. Así que podrás usar el simulador/repetición como si estuvieras operando en el mercado real. Aunque tal vez cambie algunas cosas antes de hacerlo. Pero eso se decidirá más adelante. De todos modos, debes practicar y entrenar para adquirir habilidades como programador, basado en lo que estoy tratando de mostrarte cómo hacer. Nos vemos en el próximo artículo, ya que aún tenemos que finalizar este RANDOM WALK. Aún no está completo.