Teoría de categorías (Parte 9): Acciones de monoides

Introducción

En el artículo anterior, presentamos los monoides y analizamos cómo se pueden utilizar en el aprendizaje supervisado para clasificar y fundamentar decisiones comerciales. En este artículo, estudiaremos las acciones de monoides y su aplicación en el aprendizaje no supervisado para reducir el tamaño de los datos de entrada. El resultado de las operaciones monoidales siempre resultará ser miembros del conjunto correspondiente, lo cual significa que dichas operaciones no son transformativas. Así, las acciones de monoides añadirán la capacidad de transformación, ya que el conjunto de acciones no tiene por qué ser un subconjunto del conjunto de monoides. Por transformación nos referimos a la capacidad de obtener resultados de acciones que no son miembros del conjunto de monoides.

Formalmente, una acción monoidal a de un monoide M (e, *) en un conjunto S se define como:

a: M x S - - > S ;                                (1)

e a s - - > s;                                      (2)

m * (n * s) - - > (m * n) a s                (3)

donde m, n son elementos del monoide M, mientras que s es un elemento del conjunto S.

Ilustración y métodos

Para nosotros es esencial comprender la importancia relativa de los diferentes parámetros en el proceso de toma de decisiones del modelo. En nuestro caso, de acuerdo con el artículo anterior, nuestros “parámetros” fueron:

• El periodo de análisis retrospectivo
• El marco temporal
• El precio aplicado
• El indicador
• Y la decisión de operar en un rango o con una tendencia.

Hoy veremos varios métodos que pueden usarse para ponderar las características de nuestro modelo y ayudarnos a determinar cuál es más sensible a la precisión de nuestra predicción. Seleccionaremos un método y, según sus recomendaciones, intentaremos añadir una transformación al monoide en ese nodo, ampliando el conjunto de monoides con acciones de monoides, y veremos cómo eso afecta nuestra capacidad de colocar con precisión trailing stops según las particularidades de aplicación que analizamos en el artículo anterior.

Podemos utilizar varias herramientas y técnicas para determinar la importancia relativa de cada columna de datos en el conjunto de entrenamiento. Estos métodos nos ayudarán a cuantificar la contribución de cada característica (columna de datos) a las predicciones del modelo y nos indicarán qué columna de datos puede necesitar desarrollo y cuál debería recibir menos atención. A continuación le mostramos algunos métodos utilizados habitualmente:

Clasificación de importancia del parámetro

Este enfoque clasificará los parámetros por importancia, considerando su impacto en el rendimiento del modelo. Normalmente, varios algoritmos, como los bosques aleatorios, las máquinas de aumento de gradiente (Gradient Boosting Machines) o los árboles de aumento, ofrecen medidas integradas de importancia de las características que no solo ayudan en la construcción de los árboles, sino que también se pueden extraer después de entrenar el modelo.

Para ilustrar esto, consideraremos un escenario en el que, como en el artículo anterior, queremos predecir cambios en el rango de precios y utilizar los datos resultantes para establecer un trailing stop para las posiciones abiertas. Entonces analizaremos los puntos de decisión que teníamos entonces (características o columnas de datos) como árboles. Si usamos un clasificador de bosque aleatorio para este problema, utilizando cada uno de nuestros puntos de decisión como un árbol, después del entrenamiento del modelo podremos extraer la clasificación de importancia de los parámetros.

Para mayor claridad, nuestro conjunto de datos contendrá los siguientes árboles:

• Longitud del periodo de análisis retrospectivo (datos enteros)
• Plazo seleccionado para la negociación (datos de enumeración: H1, H2, H3, etc.)
• Precio aplicado utilizado en el análisis (datos de enumeración: precio de apertura, precio medio, precio típico, precio de cierre)
• Selección del indicador utilizado en el análisis (datos de enumeración del oscilador RSI o envoltorios de Bandas de Bollinger)

Después de entrenar con un clasificador de bosque aleatorio, podemos extraer clasificaciones de importancia de las características utilizando pesos de impurezas de Gini (Gini impurity weights). Las puntuaciones de importancia de los parámetros indicarán la importancia relativa (peso) de cada columna de datos en el proceso de toma de decisiones del modelo.

Supongamos que la clasificación de importancia de los parámetros ha dado como resultado lo siguiente:

• Selección del indicador usando en el análisis: 0,45
• Duración del periodo de análisis retrospectivo: 0.30
• Precio aplicable: 0.20
• Marco temporal: 0.05

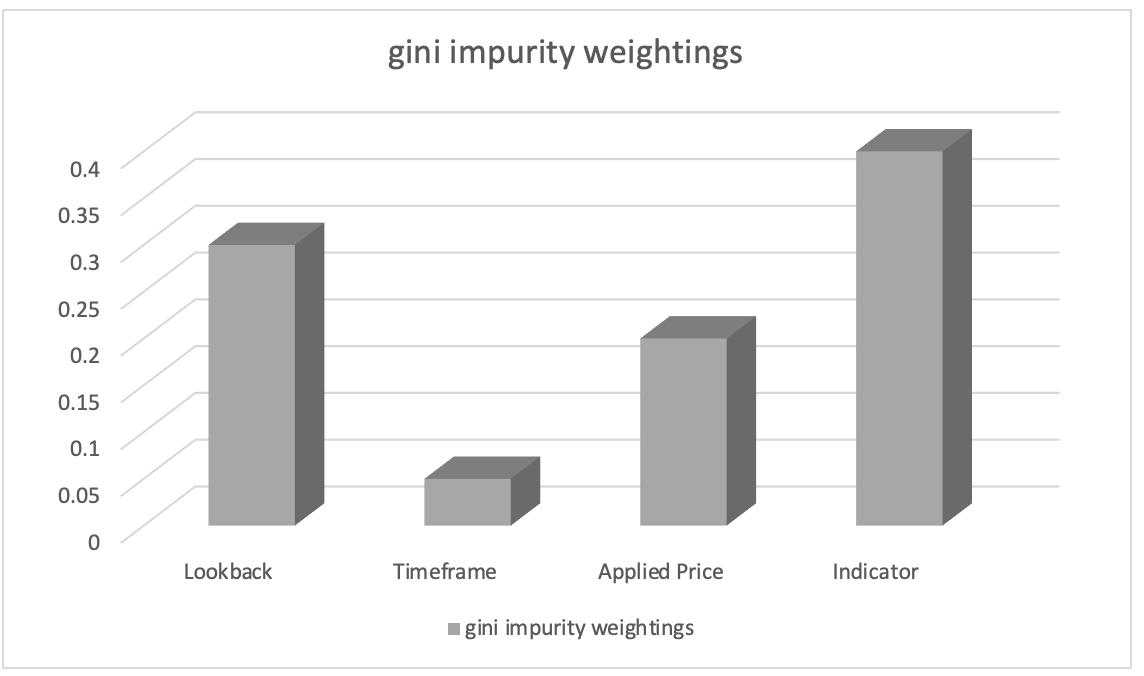
Usando como base todo esto, podemos concluir que el parámetro “elección del indicador utilizado en el análisis” tiene la mayor importancia, seguido del parámetro “duración del periodo de análisis retrospectivo”. El “precio aplicable” ocupa el tercer lugar, mientras que el “marco temporal” tiene la menor importancia.

Esta información puede ayudarnos a comprender qué parámetros resultan más importantes para las predicciones del modelo y, con este conocimiento, podremos centrarnos en los parámetros más importantes durante el desarrollo de los parámetros, priorizar la selección de los parámetros o aprender información adicional de dominio relacionada con dichos parámetros. En nuestro caso, podríamos observar la transformación del conjunto monoidal de indicadores introduciendo el(los) conjunto(s) de acción monoidal de otros indicadores y estudiando cómo esto afecta nuestras predicciones. Por lo tanto, nuestros conjuntos de acciones añadirán indicadores alternativos al oscilador RSI y al envoltorio de Bandas de Bollinger. Cualquiera que sea el indicador que añadamos, al igual que sucede con las Bandas de Bollinger en el artículo anterior, necesitaremos organizar sus datos de salida y asegurarnos de que estén en el rango de 0 a 100, donde 0 indicará una disminución del rango de la barra de precios y 100 indicará un aumento.

La importancia de la permutación

La importancia de la permutación evalúa la significación del orden de las características (o columnas de datos), cambiando aleatoriamente su orden y midiendo el cambio posterior en el rendimiento del modelo al realizar predicciones. Hasta ahora, el orden ha sido: periodo de análisis retroactivo, marco temporal, precio aplicado, indicador y, finalmente, tipo de solución comercial. ¿Qué pasaría si cambiáramos la secuencia de nuestras decisiones? Tendríamos que reorganizar una columna de datos (parámetro) cada vez. Un mayor descenso en la precisión del pronóstico para cualquiera de estas columnas de datos indicaría una mayor importancia. Este método es independiente del modelo y se puede aplicar a cualquier algoritmo de aprendizaje automático.

Para ilustrar lo dicho, consideraremos un escenario con el mismo conjunto de datos de cinco columnas que hemos visto más arriba (y en el artículo anterior). Queremos predecir los cambios en el rango de la barra de precios. Para esta tarea, hemos decidido utilizar el Clasificador de aumento de gradiente. Así, entrenaremos nuestro modelo para estimar la importancia de cada columna de datos utilizando la importancia de la permutación. Al entrenar un clasificador de aumento de gradiente utilizando las características del operador monoidal y la configuración de identificación que usamos en nuestro artículo anterior, nuestro conjunto de datos se parecerá a la siguiente tabla:

Para entrenar un clasificador de aumento de gradiente utilizando nuestro conjunto de datos, podemos seguir la siguiente guía paso a paso:

Datos de preprocesamiento :

Este paso comenzará convirtiendo nuestros datos discretos (es decir, las enumeraciones, el marco temporal del gráfico de precios, el precio aplicado, la selección de indicadores, la decisión comercial) en representaciones numéricas utilizando métodos como la codificación one-hot. Luego dividiremos el conjunto de datos en parámetros (columnas de datos de 1 a 5) y previsiones de modelo, además de los valores reales (columnas de datos de 6 a 7).

Separación de datos: Después del preprocesamiento, deberemos dividir el conjunto de datos en filas para el conjunto de entrenamiento y para el conjunto de prueba. Esto nos permitirá evaluar el rendimiento del modelo con datos no vistos utilizando la configuración que funcione mejor en sus datos de entrenamiento. Normalmente se usa una división de 80-20, pero podemos ajustar la proporción según el tamaño y las características de las filas de nuestro conjunto de datos. Para las columnas de datos usadas en este artículo, recomendaría una división de 60-40.

Creando un Clasificador de aumento de gradiente: Luego incluiremos las bibliotecas necesarias o implementaremos las funciones necesarias para la clasificación del aumento de gradiente en C/MQL5. Esto significará incluir en la función de inicialización del experto los ejemplares generados del modelo de clasificador de aumento de gradiente donde también especificamos hiperparámetros tales como el número de funciones de puntuación, la tasa de aprendizaje y la profundidad máxima.

Modelo de entrenamiento: Al iterar sobre los datos de entrenamiento y reordenar cada columna de datos durante el proceso de decisión, el conjunto de entrenamiento se utilizará para entrenar el clasificador de aumento de gradiente. Luego se registrarán los resultados del modelo. Para mejorar la precisión de las predicciones del ajuste del rango de la barra de precios, también podremos variar los parámetros del modelo, como el elemento de identificación de cada monoide o el tipo de operación (de la lista de operaciones utilizada en el artículo anterior).

Clasificación del sistema: El modelo se probará en las filas de datos de prueba (40% separadas en la división) utilizando la mejor configuración del entrenamiento. Esto nos permitirá determinar cómo de bien funcionan las configuraciones del modelo entrenado con los datos no entrenados. Al hacerlo, analizaremos todas las filas de datos fuera de la muestra (filas de datos de prueba) para evaluar la capacidad de la mejor configuración del modelo de predecir los cambios en el rango de barras de precios objetivo. Los resultados de las pruebas se podrán evaluar utilizando métodos como la medida F, etcétera

También podremos ajustar el modelo si tenemos que mejorar el rendimiento cambiando los hiperparámetros del clasificador de aumento de gradiente. Para encontrar los mejores hiperparámetros, deberemos utilizar técnicas como la búsqueda en cuadrícula y la validación cruzada. Una vez que hayamos desarrollado un modelo exitoso, podremos usarlo para hacer suposiciones sobre datos nuevos e inesperados preprocesando y codificando variables categóricas en los nuevos datos para garantizar que tengan el mismo formato que los datos de entrenamiento. De esta forma, podremos predecir cambios en el rango de la barra de precios para los datos nuevos utilizando el modelo entrenado.

Tenga en cuenta que implementar la clasificación de aumento de gradiente en MQL5 desde cero puede resultar complejo y ocupar mucho tiempo. Por lo tanto, le recomendamos encarecidamente utilizar bibliotecas de aprendizaje automático escritas en C, como XGBoost o LightGBM, que ofrecen implementaciones eficientes de aumento de gradiente con API para C.

Imaginemos, a modo de ilustración, que tras reorganizar las columnas de datos obtenemos los siguientes resultados:

• Al cambiar el periodo de análisis retrospectivo, la eficiencia del pronóstico cae en 0,062.
• El marco temporal para la permutación da como resultado una penalización del rendimiento de 0,048.
• La aplicación de una permutación al precio aplicado da como resultado una penalización del rendimiento de 0,027.
• El rendimiento cae en 0,014 al barajar la posición de las columnas de datos del indicador.
• La pérdida de rendimiento tras cambiar la decisión comercial resulta en 0,009

Estos resultados nos llevan a concluir que el "periodo de análisis retrospectivo" es más importante en su posición a la hora de predecir cambios en el rango de la barra de precios, ya que la reorganización de sus valores ha provocado la mayor disminución en el rendimiento del modelo. El segundo parámetro más importante es el “marco temporal”, seguido del “precio aplicado”, el “indicador” y finalmente la “solución comercial”.

Gracias a la cuantificación del impacto de cada columna de datos en el rendimiento del modelo, este método nos permite determinar su importancia relativa. Evaluando la importancia relativa de cada parámetro (columna de datos), podremos seleccionar las mejores funciones, diseñar características e incluso destacar las áreas donde nuestro modelo de predicción necesite más investigación y desarrollo.

Por consiguiente, podríamos proponer acciones monoidales para el conjunto de monoides de análisis retrospectivo que lo modifiquen añadiendo periodos de análisis retrospectivo adicionales que aún no estén en el conjunto de monoides para explicar adicionalmente la mejora. Así, esto nos permitirá examinar si estos periodos adicionales (si los hay) afectan a lo bien que nuestro modelo predice cambios en el rango de las barras de precios. El conjunto de monoides actualmente consta de valores que van del 1 al 8, cada uno de los cuales es múltiplo de 4. ¿Y si nuestro multiplicador fuera igual a 3 o 2? ¿Cómo afectaría esto al rendimiento, cómo le influiría en general? Puesto que ahora entendemos el lugar que ocupa el periodo retrospectivo en el proceso de toma de decisiones y que este es más sensible al rendimiento general del sistema, podremos abordar los problemas mencionados y otros adicionales.

Valores SHAP

Los valores SHAP (SHapley Additive exPlanations) son un frame unificado que asigna valores de importancia a cada columna de datos basándose en los principios de la teoría de juegos. Los valores SHAP ofrecen una distribución justa de las contribuciones de los parámetros, teniendo en cuenta todas las posibilidades. Asimismo, proporcionan una visión completa de la importancia de los parámetros en modelos complejos como XGBoost, LightGBM o modelos de aprendizaje profundo.

Eliminación recursiva de características (RFE)

La RFE es un método iterativo de selección de características que funciona eliminando recursivamente las características menos importantes según sus pesos o puntuaciones de importancia. El proceso continuará hasta alcanzar la cantidad deseada de funciones o un determinado umbral de rendimiento. Para ilustrar esto, podemos usar un escenario similar al anterior, donde tendremos un conjunto de datos de cinco columnas desde el periodo de análisis retrospectivo hasta el tipo de decisión comercial, y queremos predecir los cambios en el rango de la barra de precios según cada una de las cinco características (columnas de datos). Para esta tarea utilizaremos el clasificador de máquina de vectores de soporte (SVM). Así es como se aplicaría la eliminación recursiva de características (RFE):

• Entrenaremos el modelo utilizando un clasificador SVM utilizando todas las columnas de datos del conjunto de datos. Inicialmente, todo lo que esté disponible se utilizará para la entrenamiento.
• Luego vendrá la clasificación de características donde obtendremos los pesos o puntuaciones de importancia asignados a cada característica por el clasificador SVM. Estos indican la importancia relativa de cada uno en una tarea de clasificación.
• Luego se efectuará la eliminación de las características menos importantes, donde omitiremos la columna de datos menos importante según los pesos de SVM. Esto se puede hacer quitando el elemento con menor peso.
• Después, el modelo se reentrenará con las columnas de datos reducidas, donde el clasificador SVM se aplicará solo a las características restantes.
• La evaluación del rendimiento sin la columna de datos faltante se realizará utilizando la métrica de evaluación correspondiente, como la precisión o la medida F.
• El proceso se repetirá desde los pasos 2 al 5 hasta alcanzar el número deseado de columnas, eliminando las características (o columnas de datos) menos importantes en cada iteración y reentrenando el modelo con un conjunto reducido de características.

Por ejemplo, supongamos que comenzamos con cinco funciones, aplicamos la RFE y tenemos un objetivo de tres características. En la iteración 1, supondremos que se trata de una clasificación de características basada en una puntuación de importancia descendente:

• Periodo de análisis retrospectivo
• Marco temporal
• Precio aplicado
• Indicador
• Solución comercial

Se eliminará la característica con la calificación de importancia más baja: la decisión comercial. A esto le seguirá el reentrenamiento del clasificador SVM con las características restantes: análisis retrospectivo, marco temporal, precio aplicado e indicador. Tomaremos esto como la clasificación en la iteración 2:

• Periodo de análisis retrospectivo
• Indicador
• Marco temporal
• Precio aplicado

Eliminaremos la función con la calificación de importancia más baja. Este será el precio aplicado. Ya no quedan características que eliminar: hemos alcanzado el número deseado de características, por lo que la iteración se detendrá. El proceso iterativo se detendrá cuando alcancemos el número deseado de características (u otro criterio de parada predefinido, como el umbral de medida F). Así, el modelo final se entrenará utilizando las características seleccionadas: el periodo de análisis retrospectivo, el indicador y el marco temporal. La RFE ayuda a identificar las características más importantes para una tarea de clasificación eliminando iterativamente las características menos importantes. Seleccionando el subconjunto de características que más impactan en el rendimiento del modelo, la RFE puede mejorar el rendimiento del mismo, reduciendo el sobreajuste y mejorando la interpretabilidad.

Regularización L1 (Lasso)

La regularización L1 aplica un término de penalización a la función objetivo del modelo, incentivando los pesos de características escasos. Como resultado, las características menos importantes tienden a tener un peso de cero o cercano a cero, lo cual permite seleccionar características según la magnitud de los pesos. Vamos a considerar un escenario en el que a un tráder le gustaría calcular el riesgo de sus inversiones en bienes raíces y fideicomisos de inversión inmobiliaria. Tenemos un conjunto de datos de precios de la vivienda que queremos utilizar para predecir las tendencias de los precios de la vivienda según diversas características, como superficie, número de dormitorios, número de baños, ubicación y antigüedad. Podemos usar la regularización L1, concretamente el algoritmo Lasso, para evaluar la importancia de estas características. Así es como funciona:

• Comenzaremos entrenando un modelo de regresión lineal con la regularización L1 (Lasso) utilizando todas las características del conjunto de datos. El término de regularización L1 añadirá una penalización a la función objetivo del modelo.
• Tras entrenar el modelo Lasso, obtendremos los pesos estimados asignados a cada característica. Estos pesos reflejarán la importancia de cada característica en la predicción de los precios de la vivienda. La regularización L1 fomentará los pesos escasos para las características, lo cual significará que las características menos importantes tenderán a tener pesos nulos o cercanos a cero.
• Clasificación de características: Podemos clasificar las características según la magnitud de sus pesos. Las características con pesos absolutos más altos se considerarán más importantes, mientras que las características con pesos cercanos a cero se considerarán menos importantes.

Supongamos que entrenamos un modelo de Lasso con un conjunto de datos de precios de la vivienda y obtenemos los siguientes pesos de características:

• Superficie: 0,23
• Numero de dormitorios: 0,56
• Número de baños: 0,00
• Ubicación: 0.42
• Edad: 0,09

Usando estos pesos como base, podremos clasificar las características según su importancia para predecir los precios de la vivienda:

• Numero de dormitorios: 0,56
• Ubicación: 0.42
• Superficie: 0,23
• Edad: 0,09
• Número de baños: 0,00

En este ejemplo, el número de dormitorios tiene el peso absoluto más alto, lo cual indica su gran importancia en la predicción de los precios de la vivienda. Luego viene la ubicación y la superficie, mientras que la edad tiene relativamente menos peso. El número de baños en este caso tiene un peso de cero, lo cual indica que se considera carente de importancia y efectivamente queda excluido del modelo.

Al aplicar la regularización L1 (Lasso), podemos identificar y seleccionar las características más importantes para predecir los precios de la vivienda. La penalización de regularización posibilita la escasez de pesos de las características, lo cual permitirá la selección de características según el tamaño de los pesos. Este método ayudará a comprender qué características influyen más en la variable objetivo (tendencia del precio de la vivienda) y podría ser útil para el desarrollo de las características, la interpretación del modelo y, potencialmente, mejorar el rendimiento del modelo al reducir el sobreajuste.

Principal Component Analysis (PCA)

El PCA es un método de reducción de la dimensionalidad que puede estimar indirectamente la importancia de las características transformando las características originales en un espacio de menor dimensionalidad. El PCA determina las direcciones de máxima varianza. Los componentes principales con mayor varianza podrán considerarse más importantes.

Análisis de correlación

El análisis de correlación examina la relación lineal entre las características y una variable objetivo. Las características con valores de correlación absoluta más altos a menudo se consideran más importantes para predecir la variable objetivo. No obstante, debemos señalar que la correlación no refleja relaciones no lineales.

Información mutua

La información mutua mide la dependencia estadística entre variables, cuantificando cuánta información sobre una variable se puede obtener de otra. Los valores de información mutua más altos indican una relación más fuerte y pueden utilizarse para evaluar la importancia relativa de las características.

Para ilustrar mejor lo dicho, podemos considerar un escenario en el que un tráder/inversor busca abrir una posición en una startup de capital privado en crecimiento basándose en un conjunto de datos de clientes con el objetivo de predecir la pérdida de clientes según varias características disponibles (nuestras columnas de datos), como la edad, el sexo, los ingresos, el tipo de suscripción y el número total de compras. Podemos usar la información mutua para evaluar su importancia. Así es como funcionará:

• Comenzaremos calculando la información mutua entre cada característica y la variable objetivo (abandono de clientes). La información mutua medirá la cantidad de información que contiene una variable sobre otra. En nuestro caso, cuantificará la cantidad de información sobre el abandono de clientes que se puede obtener de cada característica en nuestras columnas de datos disponibles.
• Una vez hayamos definido las métricas de información mutua, las clasificaremos según sus valores. Los valores más altos de información mutua indicarán una relación más fuerte entre la característica y el abandono, lo cual sugerirá una mayor importancia.

Supongamos que las estimaciones de información mutua para las columnas de datos son las siguientes:

• Edad: 0,08
• Sexo: 0,03
• Ingresos: 0,12
• Tipo de suscripción: 0,10
• Compras totales: 0,15

Usando como base estos datos, podremos clasificar las características según su importancia para predecir la pérdida de clientes:

• Compras totales: 0,15
• Ingresos: 0,12
• Tipo de suscripción: 0,10
• Edad: 0,08
• Sexo: 0,03

En este ejemplo, el número total de compras tiene la puntuación de información mutua más alta, lo que indica que esta dimensión contiene la mayor información sobre el abandono de clientes. Le siguen de cerca los ingresos y el tipo de suscripción, mientras que la edad y el sexo reciben puntuaciones de información mutua relativamente más bajas.

Usando información mutua, podremos ponderar cada columna de datos y explorar qué columnas se pueden seguir explorando añadiendo acciones monoidales. Este conjunto de datos será completamente nuevo, a diferencia del conjunto del artículo anterior, por lo que, con fines ilustrativos, resultará útil construir primero los monoides de cada columna de datos definiendo los conjuntos correspondientes. El número total de compras con el valor de información mutua presumiblemente más alto serán datos continuos en lugar de discretos, lo cual significa que no podremos hacer crecer el conjunto de monoides tan fácilmente introduciendo enumeraciones fuera de la zona de acción en el monoide básico. Por lo tanto, para explorar o ampliar aún más el número total de compras en el monoide, podríamos añadir una dimensión de la fecha de compra. Esto significa que nuestro conjunto de acciones tendrá datos continuos de fecha y hora. Realizando una vinculación (a través de una acción) con el monoide en las compras totales, para cada compra podríamos obtener su fecha, lo que nos permitiría estudiar el impacto de las fechas y los montos de las compras en el abandono de clientes. Esto podría mejorar la precisión de los pronósticos.

Métodos específicos del modelo

Algunos algoritmos de aprendizaje automático tienen métodos especiales para determinar la importancia de las características. Por ejemplo, los algoritmos de árboles de decisión pueden ofrecer puntuaciones sobre la importancia de las características según el número de veces que se utilice la característica para dividir los datos en diferentes árboles.

Vamos a considerar un escenario en el que tenemos un conjunto de datos con información del cliente y queremos predecir si el cliente comprará un producto en función de diversas características como la edad, el sexo, los ingresos o el historial de navegación. Para esta tarea, hemos decidido utilizar un clasificador de bosque aleatorio, que es un algoritmo basado en árboles de decisión. Así es como podemos determinar la importancia de una característica utilizando este clasificador:

• Comenzamos entrenando un clasificador de bosque aleatorio utilizando todas las funciones del conjunto de datos. El bosque aleatorio es un algoritmo conjunto que combina múltiples árboles de decisión.
• Tras entrenar un modelo de bosque aleatorio, podremos extraer las puntuaciones de importancia de características específicas de ese algoritmo. Las puntuaciones de importancia de características indicarán la importancia relativa de cada característica en una tarea de clasificación.
• Luego clasificaremos las características según sus puntuaciones de importancia. Las características con puntuaciones más altas se considerarán más importantes porque tendrán un mayor impacto en el rendimiento del modelo.

Por ejemplo, tras entrenar un clasificador de bosque aleatorio, obtendremos las siguientes puntuaciones de importancia de las características:

• Edad: 0,28
• Sexo: 0,12
• Ingresos: 0,34
• Historial de navegación: 0,46

Usando como base estas puntuaciones de importancia de las características, podremos clasificar las características según su importancia para predecir las compras de los clientes:

• Historial de navegación: 0,46
• Ingresos: 0,34
• Edad: 0,28
• Sexo: 0,12

En este ejemplo, el historial de navegación tiene la puntuación de importancia más alta, lo cual indica que supondrá la característica más influyente a la hora de predecir las compras de los clientes. Le sigue el nivel de ingresos, mientras que la edad y el sexo tienen puntuaciones de menor importancia. Utilizando ciertas técnicas de los algoritmos de bosque aleatorio, podremos obtener las puntuaciones de importancia de las características según el número de veces que se utilice cada característica para dividir los datos en los diferentes árboles del conjunto. Esta información nos permitirá identificar las características clave que más contribuyan a la tarea de predicción. Esto, a su vez, nos ayudará con la selección de las características, la comprensión de los patrones subyacentes en los datos y, potencialmente, la mejora del rendimiento del modelo.

Conocimiento y comprensión del dominio de estudio

Además de los métodos cuantitativos, el conocimiento y la comprensión del dominio resultan fundamentales para evaluar la importancia de las características. Los expertos en el dominio de estudio siempre podrán evaluar la relevancia y la importancia de características específicas según su conocimiento y experiencia. También será importante considerar que diferentes métodos pueden producir resultados ligeramente distintos, y que la elección del método puede depender de las características específicas del conjunto de datos y del algoritmo de aprendizaje automático utilizado. Con frecuencia se recomienda utilizar varios métodos para obtener una comprensión completa de la importancia de los parámetros.

Implementación

Para implementar la ponderación de nuestras columnas de datos/parámetros, utilizaremos la correlación. Como estamos siguiendo los mismos parámetros que en el artículo anterior, compararemos la correlación de los valores del conjunto de monoides con los cambios en el rango de la barra de precios para obtener el peso de cada columna de datos. Recuerde que cada columna de datos es un monoide con un conjunto, donde los valores del conjunto son los valores de la columna. Como se trata de una prueba, al principio no sabremos si la columna más correlacionada debe expandirse (transformada por acciones monoidales) o debe ser la columna de datos con la menor correlación. Con este fin, añadiremos un parámetro adicional que ayudará a realizar esta elección para diferentes pasadas de prueba. También hemos introducido parámetros globales adicionales para gestionar acciones monoidales.

//+------------------------------------------------------------------+
//|                                                   TrailingCT.mqh |
//|                   Copyright 2009-2013, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Math\Stat\Math.mqh>
#include <Expert\ExpertTrailing.mqh>
#include <ct_9.mqh>
// wizard description start
//+------------------------------------------------------------------+
//| Description of the class                                         |
//| Title=Trailing Stop based on 'Category Theory' monoid-action concepts  |
//| Type=Trailing                                                    |
//| Name=CategoryTheory                                              |
//| ShortName=CT                                                     |
//| Class=CTrailingCT                                                |
//| Page=trailing_ct                                                 |
//|....	
//| Parameter=IndicatorIdentity,int,0, Indicator Identity            |
//| Parameter=DecisionOperation,int,0, Decision Operation            |
//| Parameter=DecisionIdentity,int,0, Decision Identity              |
//| Parameter=CorrelationInverted,bool,false, Correlation Inverted   |
//+------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//| Class CTrailingCT.                                               |
//| Appointment: Class traling stops with 'Category Theory'          |
//|               monoid-action concepts.                            |
//| Derives from class CExpertTrailing.                              |
//+------------------------------------------------------------------+
int                        __LOOKBACKS[8] = {1,2,3,4,5,6,7,8};
ENUM_TIMEFRAMES            __TIMEFRAMES[8] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES[4] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE };
string                     __INDICATORS[2] = { "RSI", "BOLLINGER_BANDS" };
string                     __DECISIONS[2] = { "TREND", "RANGE" };

#define                    __CORR 5
int                        __LOOKBACKS_A[10] = {1,2,3,4,5,6,7,8,9,10};
ENUM_TIMEFRAMES            __TIMEFRAMES_A[10] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES_A[5] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE, PRICE_WEIGHTED };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CTrailingCT : public CExpertTrailing
  {
protected:
   //--- adjusted parameters
   double m_step;                // trailing step
   
   ...
   
   //
   
   CMonoidAction<double,double>  m_lookback_act;
   CMonoidAction<double,double>  m_timeframe_act;
   CMonoidAction<double,double>  m_appliedprice_act;
   
   bool                          m_correlation_inverted;
   
   int                           m_lookback_identity_act;
   int                           m_timeframe_identity_act;
   int                           m_appliedprice_identity_act;
   
   int                           m_source_size;       // Source Size

public:
   //--- methods of setting adjustable parameters
   
   
   
   
... 
   
   void                 CorrelationInverted(bool value)     { m_correlation_inverted=value;                 }
   
   
... 
   
  };

Además, las funciones Operate_X se han reducido a una única función llamada Operate. Asimismo, hemos ampliado las funciones Get para las columnas de datos para dar cabida a acciones monoidales y hemos añadido para cada una de ellas una sobrecarga que ayudará a indexar los arrays correspondientes de las variables globales.

Nuestra clase final tendrá este aspecto.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate(CMonoid<double> &M,EOperations &O,int &OutputIndex)
   {
      OutputIndex=-1;
      //
      double _values[];
      ArrayResize(_values,M.Cardinality());ArrayInitialize(_values,0.0);
      //

      
... 
      
      //
      
      if(O==OP_LEAST)
      {
         OutputIndex=0;
         double _least=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_least>_values[i]){ _least=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_MOST)
      {
         OutputIndex=0;
         double _most=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_most<_values[i]){ _most=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_CLOSEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _closest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_closest>fabs(_values[i]-_mean)){ _closest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
      else if(O==OP_FURTHEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _furthest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_furthest<fabs(_values[i]-_mean)){ _furthest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback(CMonoid<double> &M,int &L[])
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      
... 
   
      int _i_out=-1;
      //
      Operate(M,m_lookback_operation,_i_out);
      
      if(_i_out==-1){ return(4); }
      
      return(4*L[_i_out]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(CMonoid<double> &M, ENUM_TIMEFRAMES &T[])
   {
      
... 
      
      int _i_out=-1;
      //
      Operate(M,m_timeframe_operation,_i_out);
      
      if(_i_out==-1){ return(INVALID_HANDLE); }
      
      return(T[_i_out]);
   }

Si ejecutamos las pruebas como hicimos en el artículo anterior, para EURUSD en el marco temporal de horas del 01.05.2022 al 15.05.2023, utilizando la clase de señal RSI integrada en la biblioteca, el informe se verá así.

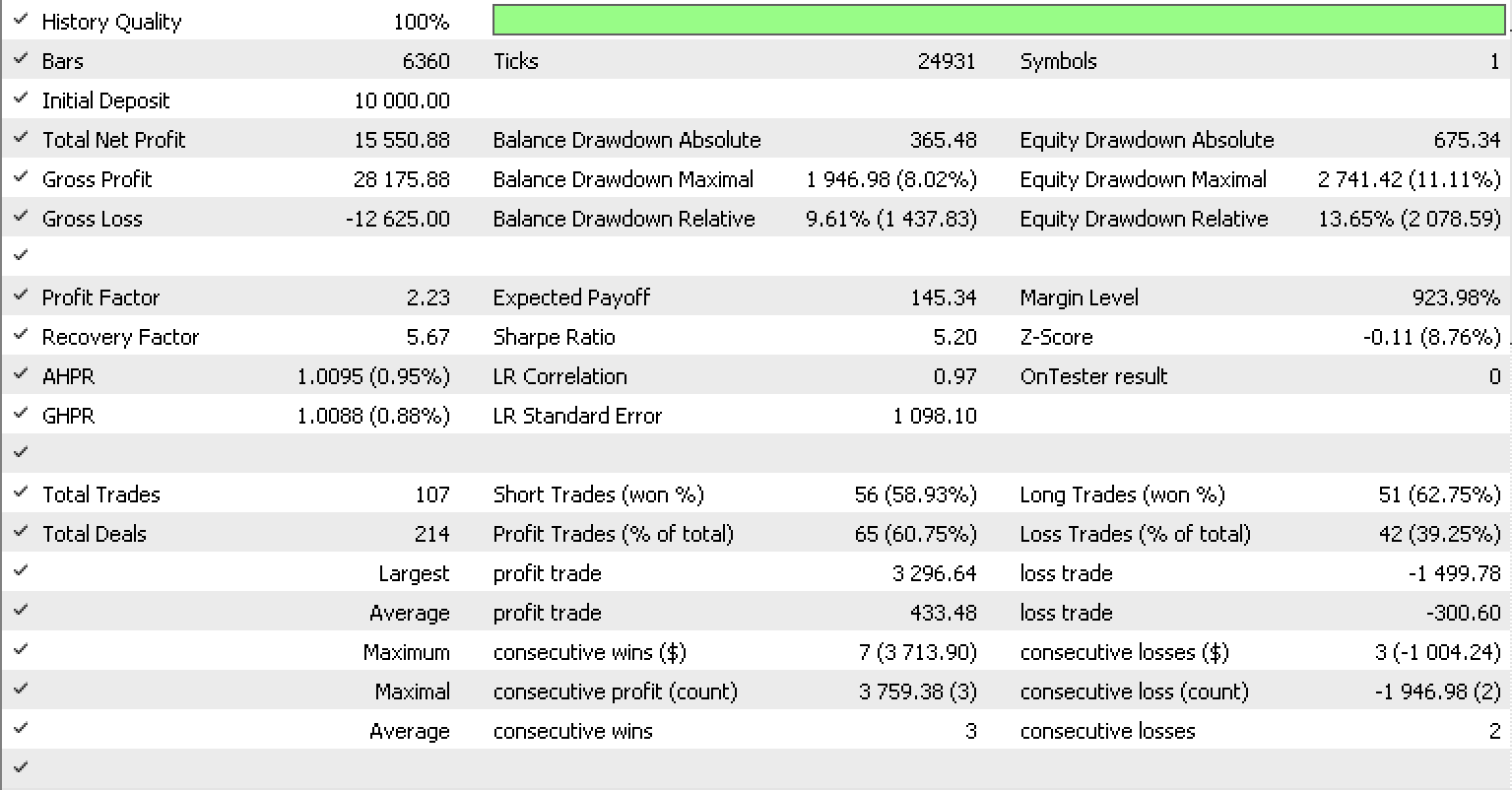
Conclusión

Hoy hemos observado cómo los monoides transformados, también conocidos como acciones monoidales, pueden mejorar aún más un sistema de trailing stop que realiza predicciones de volatilidad para ajustar con mayor precisión el stop loss de las posiciones abiertas. También hemos analizado los diversos métodos usados comúnmente para ponderar funciones de parámetros (columnas de datos, en nuestro caso), para comprender mejor el modelo, su sensibilidad y qué parámetros, si corresponde, deben ampliarse para mejorar la precisión del modelo. ¡Gracias por su atención!