Desarrollo de un sistema de repetición — Simulación de mercado (Parte 15): Nacimiento del SIMULADOR (V) - RANDOM WALK

Introdução

En los últimos artículos de esta serie sobre el desarrollo de un sistema de repetición del mercado, he mostrado cómo simular, o mejor dicho, cómo generar algún tipo de modelado virtual de un activo específico. El objetivo es lograr un movimiento lo más cercano posible a lo que sería un movimiento real. A pesar de haber avanzado significativamente, pasando de un sistema simple, muy similar al utilizado por el simulador de estrategias, a un modelo bastante interesante, todavía no hemos logrado crear un modelado que se adapte a cualquier conjunto de datos. Necesitamos que sea lo suficientemente dinámico y estable al mismo tiempo para permitirnos generar diversas situaciones posibles con el mínimo esfuerzo en términos de programación.

Lo que haremos aquí es corregir una falla que existe en el artículo "Desarrollo de un sistema de repetición — Simulación de mercado (Parte 14): Nacimiento del SIMULADOR (IV)". A pesar de haber generado un primer principio de RANDOM WALK, no es del todo adecuado cuando estamos trabajando con valores que están previamente definidos en un archivo o base de datos. En nuestro caso específico, nuestra base de datos siempre indicará las métricas que debemos utilizar y respetar. A pesar de que el sistema RANDOM WALK, visto y desarrollado, puede generar movimientos muy similares a los que se ven en un mercado real, no es adecuado para ser utilizado en un simulador de movimientos. La razón de esto es que no puede cubrir completamente el rango que debe ser cubierto en todos los casos. Es cierto que en casos muy raros, tendremos la cobertura completa de todo el rango, yendo desde el precio de apertura hacia la máxima o mínima, cambiando de dirección por completo una vez que alcance uno de los límites y yendo al otro extremo. Finalmente, de manera casi mágica, encontrará y se detendrá exactamente en el precio definido como el cierre de la barra.

Puede parecer imposible que esto ocurra, pero ocasionalmente sucederá. Sin embargo, no podemos depender de la casualidad. Necesitamos que siga siendo lo más aleatorio posible y permitido. Al mismo tiempo, necesitamos que cumpla su función, que es cubrir de manera total e integral los puntos predefinidos en la barra. Pensando de esta manera y analizando algunos conceptos matemáticos abstractos, podemos generar una forma relativamente atractiva de un RANDOM WALK controlado. Al menos en lo que respecta al hecho de que todos los puntos de interés y definidos serán alcanzados y respetados.

La idea en sí no es complicada, aunque bastante inusual. No voy a entrar en detalles matemáticos innecesarios para no complicar la explicación. Sin embargo, te mostraré el concepto que se utilizará, junto con el código, por supuesto, para que tú también puedas comprenderlo y, quién sabe, incluso desarrollar pequeñas variaciones de lo que presentaré.

Comprendamos la idea y el concepto

Si has estado siguiendo esta serie sobre la repetición/simulador, debes haber notado que comenzamos experimentando y tratando de crear primero un sistema que pudiera cubrir todos los puntos de precio. Esto se hizo utilizando una técnica muy similar a la que se usa en el simulador de estrategias. Esta técnica se basa en el típico movimiento de zigzag, algo muy común y ampliamente conocido por quienes estudian el mercado. Para aquellos que no lo conocen o no saben de qué se trata, pueden ver una representación esquemática en la figura 01.

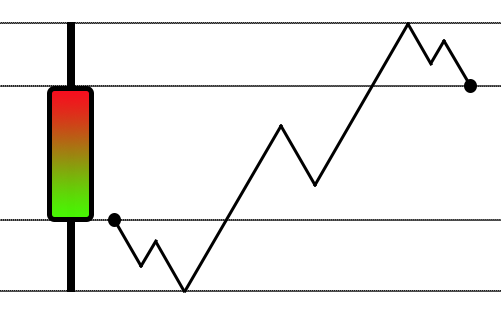
Figura 01 - Movimiento típico en zigzag

El hecho es que, a pesar de que este modelado es muy adecuado para el simulador de estrategias, está lejos de ser adecuado para un sistema de repetición/simulación. La razón es simple: la cantidad de órdenes generadas al utilizar este modelado siempre es mucho menor de lo que realmente se encontraría en un momento típico del mercado. Pero esto no significa que este modelo no sea válido, solo que no es adecuado para ser utilizado en un sistema como el que queremos desarrollar. Incluso si pudiéramos encontrar una forma de que el movimiento representado en la figura 01 generara una cantidad de órdenes equivalente a una negociación real, el movimiento en sí no sería lo suficientemente complejo. Sería simplemente una adaptación del movimiento real de la figura. Necesitamos encontrar otra forma de hacer las cosas.

Necesitamos una forma que sea lo más aleatoria posible pero que al mismo tiempo no genere una explosión de complejidad en el código a programar. Recuerda lo siguiente: si la complejidad del código crece muy rápido, se volverá rápidamente inviable de mantener y corregir. Siempre debemos esforzarnos por mantener las cosas lo más simples posible. De esta manera, podrías pensar que podríamos simplemente generar valores de precios aleatorios y así simular un nivel de complejidad suficientemente alto para que el movimiento sea lo más cercano posible al real. Sin embargo, no podemos permitirnos aceptar cualquier precio o cualquier cantidad de órdenes generadas. Siempre debemos respetar la base de datos. Siempre.

Al observar una base de datos, terminarás notando que hay información bastante útil allí. De hecho, están ahí porque son necesarios. En la figura 02, puedes ver un contenido típico de un archivo de barras. En él, estoy resaltando algunos valores que son realmente de interés.

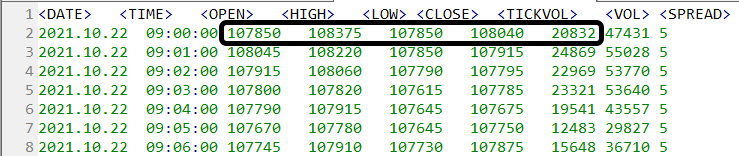
Figura 02 - Contenido típico de un archivo de barras de 1 minuto

Si tomas estos valores y generas completamente al azar los valores de precio, pero, y enfatizo esto, manteniendo las cosas dentro de un rango especificado, obtendrás un tipo de movimiento completamente aleatorio. Sin embargo, al mismo tiempo, este mismo movimiento no sería nada cómodo. Ya que rara vez, un mercado real tendrá tal tipo de movimiento.

Para que no te quedes solo imaginando lo que se está generando, podemos traducir esto a un formato de gráfico. El resultado de una generación completamente aleatoria de precios dentro de un rango dado se vería como se muestra en la figura 03.

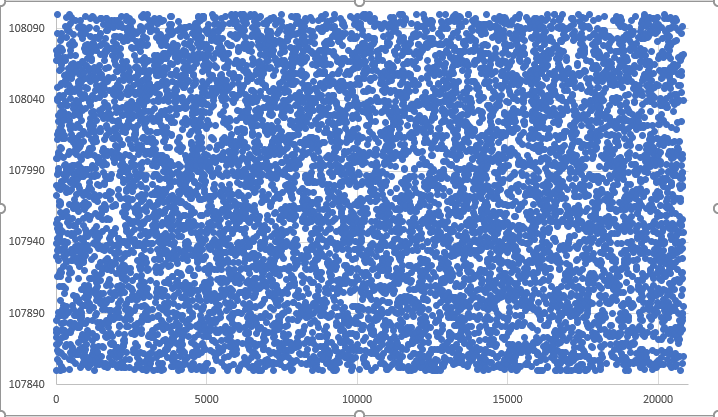
Figura 03 - Gráfico del resultado de valores totalmente aleatorios

Este tipo de gráfico se puede obtener utilizando un método bastante simple pero al mismo tiempo muy efectivo. Ya he mostrado en el pasado cómo hacerlo en Excel, para que puedas generar este tipo de gráfico. Esto te ayudará a analizar con mayor precisión el movimiento que se está construyendo, basándote únicamente en los valores de una base de datos. Realmente vale la pena aprender a hacer esto, ya que es esencial para que puedas analizar de manera más rápida valores completamente aleatorios. Sin este recurso, te sentirías completamente perdido en la inmensa cantidad de datos, tratando de entender toda esa confusión aparentemente sin sentido.

Una vez que sepas cómo generar esos gráficos, empiezas a analizar la situación con más calma. Y te das cuenta de que el gráfico que se muestra en la figura 03 no es realmente adecuado para nuestro sistema debido al alto nivel de aleatoriedad presente en él. Entonces comienzas a buscar una forma de al menos contener esa aleatoriedad para que podamos generar algo más parecido a un movimiento real. Después de un tiempo, descubrirás un método, uno que se utiliza mucho en viejos videojuegos donde un personaje aparentemente se mueve de manera aleatoria por el escenario del juego; pero en el fondo, lo que sucede es que el personaje sigue reglas bastante simples. Este método también se puede ver en sistemas que mezclan piezas, muy populares y divertidos, como el cubo mágico (Figura 04) o incluso juegos en 2D que utilizan piezas deslizantes para tanto resolver como mezclar el juego (Figura 05).

Figura 04 - El Cubo Mágico es un ejemplo de movimiento RANDOM WALK

Figura 05 - Rompecabezas deslizante: el sistema más simple de uso de RANDOM WALK

Aunque a primera vista, estos "juguetes" no parecen utilizar RANDOM WALK, de hecho, lo hacen. No para ser resueltos, aunque podrías resolverlos utilizando el método RANDOM WALK, llevaría mucho más tiempo que usar métodos más adecuados. Pero para que las piezas estén en posiciones aparentemente aleatorias, es necesario utilizar una formulación que involucre RANDOM WALK. Una vez hecho esto, intentas resolverlos utilizando otra metodología, como lo haría un niño al volver a colocar las piezas en el lugar adecuado. Lo mismo ocurre con el sistema de generación de órdenes utilizando RANDOM WALK. En realidad, las matemáticas detrás del sistema de movimiento RANDOM WALK son prácticamente las mismas en todos los casos, no cambian.

Lo que realmente cambia es solo el sistema de orientación que vamos a utilizar. Puedes imaginar que un movimiento aparentemente sin sentido pero que se encuentra en un espacio tridimensional no se ajustaría a esta matemática. Sin embargo, para ser honesto, son muy pocos los casos en los que esto realmente ocurre. En muchos de ellos, las matemáticas involucradas en la descripción de RANDOM WALK pueden explicar las variaciones que ocurren con el tiempo. Entonces, al usar esta matemática en un sistema de Precio x Tiempo, obtendremos un gráfico similar al de la figura 06.

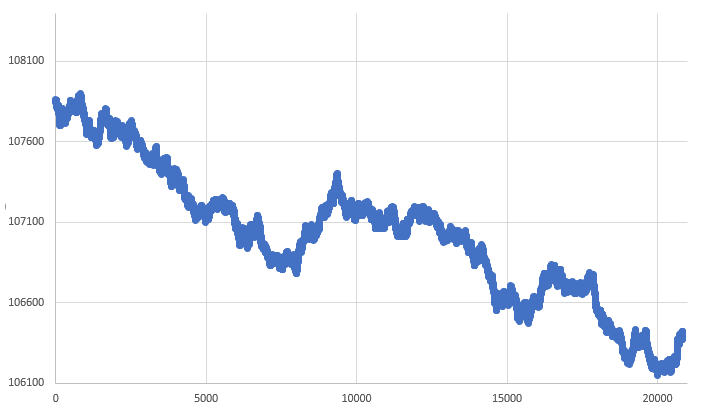
Figura 06 - RANDOM WALK de precio x tiempo

Este tipo de cosa, que sigue los mismos principios de movimientos estocásticos, se asemeja mucho al movimiento real que normalmente presenta el mercado. Pero no te engañes. El gráfico de arriba no corresponde a un activo real. Se obtiene utilizando un generador de números aleatorios. A partir del precio anterior, sumarás o restarás una unidad al precio, generando así un nuevo precio. La forma de saber si sumaremos o restaremos depende de la regla que se utilice. Puedes decir simplemente que cualquier número PAR generado aleatoriamente indicará suma y cualquier número IMPAR indicará resta. Aunque simple, esta regla logrará hacer su trabajo. Sin embargo, también puedes cambiar la regla, de modo que cualquier número generado aleatoriamente, que sea divisible por 5, indique suma; de lo contrario, tendremos una resta. Y el simple hecho de cambiar esta regla generará un gráfico completamente diferente. Incluso el valor que inicializa el sistema de generación aleatoria hace que las cosas cambien ligeramente.

Pero a pesar de que el gráfico de la figura 06 es adecuado para un sistema completamente libre, no podemos utilizarlo en un sistema de simulación. Esto se debe a que debemos respetar los valores que se indican en la base de datos. Estos nos proporcionan límites explícitos, tanto superiores como inferiores, para la generación de RANDOM WALK. Así que al hacer las correcciones para que estos límites se cumplan, pasamos del gráfico presente en la figura 06 al que se puede ver en la figura 07.

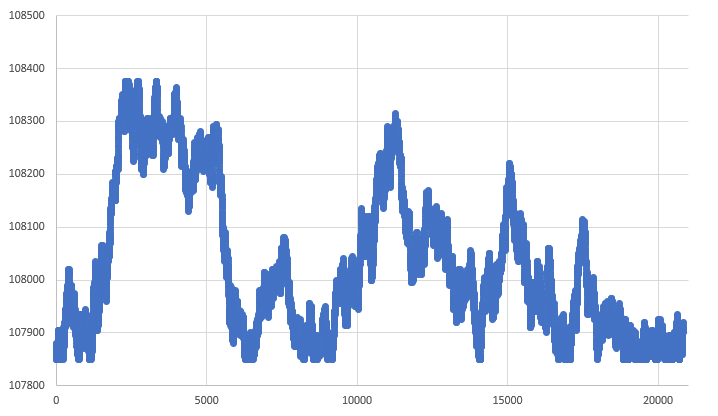
Figura 07 - RANDOM WALK dentro de límites

El sistema que genera un gráfico como se muestra en la figura 07 es mucho más adecuado para usar en un simulador. Aquí, tenemos una base de datos que nos proporciona los límites en los que podemos movernos. De hecho, a pesar de seguir utilizando matemáticas igualmente simples, logramos crear un sistema que contiene un buen nivel de complejidad. Y al mismo tiempo, no es completamente predecible, es decir, estamos en el camino correcto. Observa que, del gráfico generado en la figura 01 a este que se ve en la figura 07, lo único que realmente ha cambiado es el nivel de complejidad. O mejor dicho, la aleatoriedad presente en este último es mejor. Aunque el sistema de la figura 01 es suficiente para un simulador de estrategias, el gráfico generado y visto en la figura 07 contiene mucho más de lo necesario para un probador. Sin embargo, estas cosas son de suma importancia para un simulador.

Pero incluso con este aumento en el nivel de complejidad visto en el gráfico 07, aún no es del todo suficiente para ser utilizado en un simulador. Dado el hecho de que lo único de lo que podemos estar seguros de usar es el punto inicial. En este caso, el PRECIO DE APERTURA. Ninguno de los otros puntos indicados en la base de datos (CIERRE, MÁXIMO, MÍNIMO) puede o garantiza ser visitado. Esto es un problema, ya que para que el simulador sea realmente viable, todos los puntos indicados en la base de datos deben ser visitados con total certeza.

Con esto en mente, necesitamos hacer algo que convierta el gráfico de la figura 07 en un gráfico como el de la figura 08. Donde tengamos la certeza absoluta de que los puntos fueron realmente accedidos en algún momento.

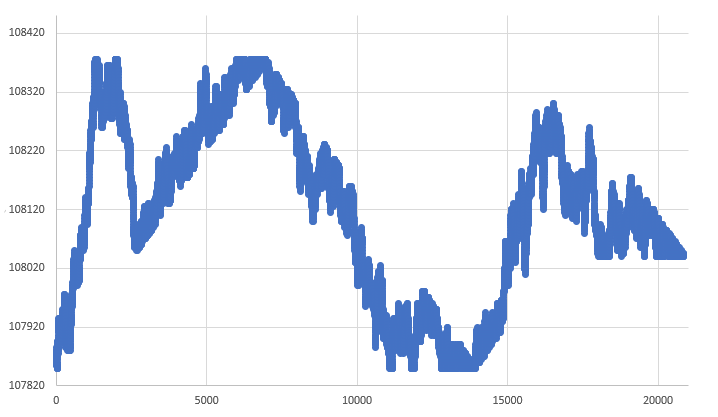
Figura 08 - RANDOM WALK forzado

Este tipo de cambio implica no más que algunos ajustes. Pero si observas detenidamente el gráfico, notarás claramente que el movimiento está siendo dirigido de alguna manera. Aún así, no podrás evitar darte cuenta de que tenemos un RANDOM WALK. No tan natural, pero aún aleatorio, como se esperaría en un movimiento estocástico. Ahora quiero que notes lo siguiente: Todos los gráficos vistos anteriormente utilizan la misma base de datos. Se muestra en la figura 02. Sin embargo, la mejor solución es la que se muestra en la figura 08. Donde realmente tenemos un movimiento que no es tan confuso ni se aleja de la base de datos como el visto en la figura 03. Aun así, sigue siendo muy similar a lo que podría haber ocurrido durante la construcción de la barra.

Basándonos en los conceptos mostrados hasta ahora, creo que realmente te he convencido de que la forma en que quedó el código en el artículo anterior no es exactamente lo que necesitamos en un simulador. Esto se debe a que algunos de los puntos pueden no ser visitados adecuadamente durante el período en el que ocurrió el movimiento aleatorio. Sin embargo, en lugar de forzar que estos puntos aparezcan en el gráfico, ¿qué te parece si dejamos las cosas un poco más naturales?

Y este es el punto que mostraré y abordaré en el próximo tema.

RANDOM WALK forzado

El hecho de llamarlo "Random Walk forzado" no significa que impondremos una condición sobre él. Sin embargo, limitaremos el movimiento de una manera bastante específica, de modo que parezca lo más natural posible, pero manteniendo su naturaleza aleatoria. Sin embargo, con un detalle: Forzaremos el movimiento hacia un punto de convergencia. Y este punto es precisamente el que debe ser visitado. De esta manera, tendremos realmente una combinación entre la figura 01 y la figura 07. ¿Te ha intrigado, verdad? Pero en realidad, no vamos a usar el camino que normalmente se crearía como en la figura 01. Vamos a utilizar un enfoque un poco diferente.

Para entenderlo realmente, veamos el código de Random Walk que se encuentra en el código del artículo anterior. Puedes verlo a continuación:

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long    il0, max;
                                double  v0, v1;
                                bool    bLowOk, bHighOk;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;                                     
                                bLowOk = bHighOk = false;
                                for (int c0 = 1; c0 < max; c0++)
                                {                               
                                        v0 = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1));
                                        if (v0 <= rate.high)
                                                v0 = tick[c0].last = (v0 >= rate.low ? v0 : tick[c0 - 1].last + m_PointsPerTick);
                                        else
                                                v0 = tick[c0].last = tick[c0 - 1].last - m_PointsPerTick;
                                        bLowOk = (v0 == rate.low ? true : bLowOk);
                                        bHighOk = (v0 == rate.high ? true : bHighOk);
                                }                                       
                                il0 = (long)(max * (0.3));
                                if (!bLowOk) tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                if (!bHighOk) tick[macroRandomLimits(max - il0, max)].last = rate.high;                         
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
#undef macroRandomLimits
                        }                       

Lo que realmente necesitamos hacer es modificar de alguna manera este código que se destaca arriba. Si se hace de manera adecuada, podremos mantener el sistema siguiendo las premisas de RANDOM WALK al tiempo que controlamos la forma en que se generará el camino. Así lograremos visitar todos los puntos que se están informando. Recuerda que el punto de apertura siempre se visitará. Lo que realmente nos preocupa son los otros 3 puntos: el máximo, el mínimo y el cierre. Entonces hagamos lo siguiente: primero, crearemos una rutina básica para reemplazar el código destacado anteriormente. Pero lo haremos de una manera mucho más interesante.

Para facilitar nuestra vida, primero crearemos una nueva rutina que será responsable de generar el RANDOM WALK. Puedes verla a continuación en su primera versión.

inline long RandomWalk(long pIn, long pOut, const MqlRates &rate, MqlTick &tick[], int iMode)
                        {
                                double vStep, vNext, price, vHigh, vLow;
                                
                                vNext = vStep = (pOut - pIn) / ((rate.high - rate.low) / m_PointsPerTick);
                                vHigh = rate.high;
                                vLow = rate.low;
                                for (long c0 = pIn, c1 = 0, c2 = 0; c0 < pOut; c0++, c1++)
                                {
                                        price = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? -1 : 1));
                                        price = tick[c0].last = (price > vHigh ? price - m_PointsPerTick : (price < vLow ? price + m_PointsPerTick : price));
                                        switch (iMode)
                                        {
                                                case 0:
                                                        if (price == rate.close)
                                                                return c0;
                                                case 1:
                                                case 2:
                                                        break;
                                        }
                                        if ((int)floor(vNext) < c1)
                                        {
                                                if ((++c2) <= 3) continue;
                                                vNext += vStep;
                                                if (rate.close > vLow) vLow += m_PointsPerTick); else vHigh -= m_PointsPerTick;
                                        }
                                }
                                
                                return pOut;
                        }

¿No entiendes lo que estoy haciendo? No te preocupes. Lo explicaré para que puedas seguir mi razonamiento. Como se dijo, esta es la primera versión. Primero, calculamos el paso que ejecutaremos para conducir el Random Walk de manera que llegue a un punto específico. Almacenamos los valores máximos y mínimos del límite en el que el Random Walk realmente estará. Ahora comienza nuestra odisea. Caminaremos una cierta cantidad de puntos de manera aleatoria. En cada paso que demos, ajustaremos las cosas, no para bloquear el Random Walk, sino para guiarlo en una especie de canal del cual no podrá salir. Puede tambalearse de un lado a otro, pero en ningún momento saldrá del canal. Cuando estamos en el modo cero, tan pronto como se alcance el punto de destino, la rutina se detendrá. Esto es importante para generar una mayor aleatorización. Pero no te preocupes, más adelante esto quedará más claro.

Ahora tenemos que hacer algo: ¿Recuerdas que hicimos un cálculo para saber cuánto tiempo llevaría reducir el canal? Bueno, ha llegado el momento de comenzar a cerrar el canal.  Este cierre se produce poco a poco, pero con un detalle bastante curioso. En realidad, no lo cerraremos por completo. Dejaremos una pequeña franja muy estrecha donde el precio podrá seguir su camino aleatorio, algo similar a las bandas de Bollinger. Pero al final, estará prácticamente en el punto indicado como el punto final, es decir, el cierre. Esto realmente sucede al cambiar los límites del canal. Primero cerramos la parte inferior y cuando llegamos al punto de salida, comenzamos a cerrar desde la parte superior.

De una forma u otra, el último punto estará prácticamente siendo accedido. Pero si no está siendo accedido, estará muy, pero muy cerca del ideal. ¿Pero dónde encaja esta rutina de arriba? Bueno, reemplazará el antiguo método de random walk. Al hacerlo, estaremos combinando lo que ocurre en la figura 01 y lo que ocurre en la figura 07. Como resultado, obtendremos una imagen muy similar a la figura 08.

Entonces, mira cómo quedó la nueva rutina de simulación.

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long    il0, max, i0, i1;
                                bool    b1 = ((rand() & 1) == 1);
                                double  v0, v1;
                                MqlRates rLocal;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;                                     
                                i0 = (long)(MathMin(max / 3.0, max * 0.2));
                                i1 = max - i0;
                                rLocal = rate;  
                                rLocal.open = rate.open;
                                rLocal.close = (b1 ? rate.high : rate.low);
                                i0 = RandomWalk(1, i0, rLocal, tick, 0);
                                rLocal.open = tick[i0].last;
                                rLocal.close = (b1 ? rate.low : rate.high);
                                RandomWalk(i0, i1, rLocal, tick, 1);
                                rLocal.open = tick[i1].last;
                                rLocal.close = rate.close;
                                RandomWalk(i1, max, rLocal, tick, 2);
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
#undef macroRandomLimits
                        }                       

El fragmento destacado es el que está reemplazando al antiguo método. Ahora viene una pregunta importante que debes entender. ¿Qué hace el fragmento destacado? ¿Puedes responder solo mirando su código?

Si puedes, genial. ¡Mis más sinceras felicitaciones! Si no puedes, entonces veamos este fragmento.

                                i0 = (long)(MathMin(max / 3.0, max * 0.2));
                                i1 = max - i0;
                                rLocal = rate;  
                                rLocal.open = rate.open;
                                rLocal.close = (b1 ? rate.high : rate.low);
                                i0 = RandomWalk(1, i0, rLocal, tick, 0);
                                rLocal.open = tick[i0].last;
                                rLocal.close = (b1 ? rate.low : rate.high);
                                RandomWalk(i0, i1, rLocal, tick, 1);
                                rLocal.open = tick[i1].last;
                                rLocal.close = rate.close;
                                RandomWalk(i1, max, rLocal, tick, 2);

Lo que se está haciendo es un GRAN zigzag. ¿Pero cómo 🤔? ¿No puedo verlo 🥺? Vamos por partes. Inicialmente, calculamos un punto límite para que la primera pierna del zigzag pueda terminar.  Una vez hecho esto, definimos de inmediato el tamaño de la tercera pierna. Un detalle: la primera pierna, a diferencia de la tercera, no tiene un tamaño fijo. Puede terminar en cualquier momento. Este momento está definido por la rutina de random walk. Pero dado que al finalizar la primera pierna, debemos comenzar la segunda, el valor devuelto por la rutina RandomWalk se utiliza como punto de inicio. Aquí tenemos una nueva llamada para construir un segundo random walk. ¿Confuso?

Calma, vamos llegar allí. Ahora definimos los límites y los puntos de entrada y salida de la primera pierna del random walk. La rutina de creación del random walk se llama y regresa tan pronto como se alcanza el punto de finalización o lo más cerca posible de él. Luego ajustamos nuevamente los puntos de entrada y salida de la próxima pierna.  Llamamos a la rutina de creación del random walk de modo que el movimiento vaya de un extremo al otro. Pero incluso si se alcanzan estos extremos, la rutina solo regresará cuando se alcance el número de posiciones definidas.  Una vez que eso suceda, definimos por tercera y última vez los puntos de entrada y salida del random walk. Realizamos la llamada que construirá la última pierna. Es decir, tenemos un gran zigzag. En lugar de que el precio vaya de un punto a otro, se sacudirá dentro de los límites que hemos definido 😁.

Al ejecutar este sistema que se explicó anteriormente, obtendrás un gráfico muy similar al de la figura 08. Lo cual no está nada mal, considerando la simplicidad del método mencionado anteriormente. Pero podemos mejorar todo esto. Si observas con atención, notarás que en el gráfico de la figura 08, hay puntos en los que el precio parece quedarse como si estuviera golpeando una pared. Esto, aunque parezca extraño, a veces ocurre en un mercado real. Específicamente, cuando uno de los lados, ya sean compradores o vendedores, no permite que el precio se mueva más allá de cierto punto, la famosa lucha de órdenes en el libro de órdenes.

Pero, y solo si deseas un movimiento un poco más natural en el sistema, tendrás que cambiar no la rutina de simulación, sino solo y exclusivamente la rutina responsable de crear el random walk. Pero aquí está el detalle en toda esta historia. No debes, y lo repetiré, NO DEBES intentar crear un nuevo método de random walk. Solo debes crear una forma de encender y apagar los límites para que el movimiento fluya por sí solo. Si se hace de manera adecuada, el resultado final será un gráfico con un aspecto mucho más natural. Como si en ningún momento estuviéramos guiando el movimiento.

Un primer intento de hacer esto es agregar una comprobación de toques en los límites. Tan pronto como eso suceda, algo mágico comenzará a ejecutarse. Así que mira cómo queda la nueva rutina de random walk, no es un nuevo método, es solo una adaptación de la rutina original. Recuerda que solo explicaré las partes nuevas 😉.

inline long RandomWalk(long pIn, long pOut, const MqlRates &rate, MqlTick &tick[], int iMode)
                        {
                                double vStep, vNext, price, vHigh, vLow;
                                
    char  i0 = 0;
                                
                                vNext = vStep = (pOut - pIn) / ((rate.high - rate.low) / m_PointsPerTick);
                                vHigh = rate.high;
                                vLow = rate.low;
                                for (long c0 = pIn, c1 = 0, c2 = 0; c0 < pOut; c0++, c1++)
                                {
                                        price = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? -1 : 1));
                                        price = tick[c0].last = (price > vHigh ? price - m_PointsPerTick : (price < vLow ? price + m_PointsPerTick : price));
                                        switch (iMode)
                                        {
                                                case 0:
                                                        if (price == rate.close)
                                                                return c0;
                                                        break;
                                                case 1:
                                                        i0 |= (price == rate.high ? 0x01 : 0);
                                                        i0 |= (price == rate.low ? 0x02 : 0);
                                                        vHigh = (i0 == 3 ? rate.high : vHigh);
                                                        vLow = (i0 ==3 ? rate.low : vLow);
                                                        break;
                                                case 2:
                                                        break;
                                        }
                                        if ((int)floor(vNext) < c1)
                                        {
                                                if ((++c2) <= 3) continue;
                                                vNext += vStep;
                                                if (rate.close > vLow) vLow = (i0 == 3 ? vLow : vLow + m_PointsPerTick); else vHigh = (i0 == 3 ? vHigh : vHigh - m_PointsPerTick);
                                        }
                                }
                                
                                return pOut;
                        }

Ahora tenemos una situación completamente nueva aquí. Por lo tanto, debemos evitar sobrepasar los antiguos límites, que antes no supondrían ningún problema sobrepasar. Pero hay un detalle muy sutil. Tenemos una nueva variable que comienza en cero. En realidad, esto sería como un conjunto booleano. Lo que hace esta modesta variable es algo asombroso. Así que presta mucha atención para poder entenderlo. Es algo muy bien definido y bastante curioso. Cuando estamos en la segunda pierna del zigzag, en algún momento el precio toca el máximo y luego el precio toca el mínimo. Entonces, en cada uno de estos toques, anotamos un valor específico en nuestra variable. Ahora, ¿qué sucede si observamos la variable no como unidades de bits, sino en su totalidad? Obtendremos un valor muy específico. Este valor puede ser Cero, Uno, Dos o Tres.

Pero espera un momento, ¿cómo es eso de Tres 🤔? El detalle es que cuando tenemos un toque en el máximo, realizamos una operación lógica OR en la que hacemos que el bit menos significativo sea verdadero. Cuando tenemos un toque en el mínimo, realizamos la misma operación, pero ahora en el segundo bit menos significativo. Es decir, si el primer bit ya tiene el valor verdadero y luego establecemos el segundo bit en verdadero, pasamos inmediatamente de un valor igual a 1 a un valor igual a 3. Por eso la cuenta llega hasta el valor 3.

Es importante comprender este hecho, ya que este será precisamente el valor que probaremos. En lugar de probar 2 booleanos diferentes, probaremos un valor que represente a ambos. ¿Comprendiste la lógica del sistema 😁? De esta manera, si el valor es igual a 3, tendremos una expansión de los límites que podrían utilizarse. O, para que lo entiendas mejor, si no hiciéramos esta prueba, los límites se cerrarían hasta que el random walk se comprimiera en solo 3 posiciones posibles de movimiento. Pero al hacer esto, permitimos que el movimiento fluya naturalmente nuevamente. Dado que los límites se han alcanzado, no tiene sentido seguir restringiendo el movimiento.

Esta explosión ocurre en estos puntos. Entonces, cuando la rutina intente reducir los límites, ya no lo hará. Ahora, el random walk ocurrirá dentro de todo el límite, lo que lo hace mucho más natural. Si ejecutas ahora el sistema con la misma base de datos que hemos estado utilizando desde el inicio del artículo, obtendrás un gráfico muy similar al que se muestra en la figura 09 😊.

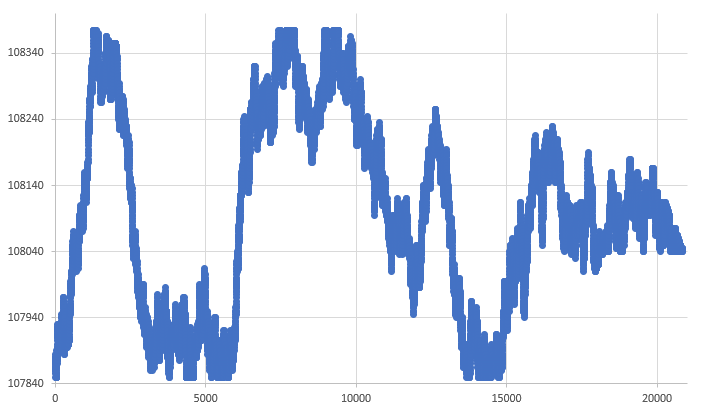
Figura 09 - Random Walk con explosión

Observa que este gráfico parece ser mucho más natural que el gráfico visto en la figura 08. Sin embargo, incluso este último gráfico, que parece ideal, aún cuenta con un punto que no es tan natural. Este punto se puede percibir en la última pierna. Presta mucha atención al final del gráfico. Notarás que parece un poco forzado, considerando los límites de movimiento posibles. Este tipo de cosa merece ser corregida. Y es precisamente lo que haremos ahora.

Para resolver esta cuestión, debemos agregar algunas líneas en la rutina responsable del random walk. Luego, la versión final del sistema se ve a continuación:

inline long RandomWalk(long pIn, long pOut, const MqlRates &rate, MqlTick &tick[], int iMode)
                        {
                                double vStep, vNext, price, vHigh, vLow;
                                char i0 = 0;
                                
                                vNext = vStep = (pOut - pIn) / ((rate.high - rate.low) / m_PointsPerTick);
                                vHigh = rate.high;
                                vLow = rate.low;
                                for (long c0 = pIn, c1 = 0, c2 = 0; c0 < pOut; c0++, c1++)
                                {
                                        price = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? -1 : 1));
                                        price = tick[c0].last = (price > vHigh ? price - m_PointsPerTick : (price < vLow ? price + m_PointsPerTick : price));
                                        switch (iMode)
                                        {
                                                case 0:
                                                        if (price == rate.close)
                                                                return c0;
                                                        break;
                                                case 1:
                                                        i0 |= (price == rate.high ? 0x01 : 0);
                                                        i0 |= (price == rate.low ? 0x02 : 0);
                                                        vHigh = (i0 == 3 ? rate.high : vHigh);
                                                        vLow = (i0 ==3 ? rate.low : vLow);
                                                        break;
                                                case 2:
                                                        break;
                                        }
                                        if ((int)floor(vNext) < c1)
                                        {
                                                if ((++c2) <= 3) continue;
                                                vNext += vStep;
                                                if (iMode == 2)
                                                {
                                                        if ((c2 & 1) == 1)
                                                        {
                                                                if (rate.close > vLow) vLow += m_PointsPerTick; else vHigh -= m_PointsPerTick;
                                                        }else
                                                        {
                                                                if (rate.close < vHigh) vHigh -= m_PointsPerTick; else vLow += m_PointsPerTick;
                                                        }
                                                } else
                                                {
                                                        if (rate.close > vLow) vLow = (i0 == 3 ? vLow : vLow + m_PointsPerTick); else vHigh = (i0 == 3 ? vHigh : vHigh - m_PointsPerTick);
                                                }
                                        }
                                }
                                
                                return pOut;
                        }

Parece un poco loco, pero mira lo siguiente: Cuando estamos ejecutando la primera y la segunda pierna, el código que realmente se ejecutará es este. Cuando estamos en la tercera pierna, tendremos una figura un poco diferente.

Para crear realmente la figura que en el análisis gráfico se conoce como TRIÁNGULO SIMÉTRICO, debemos reducir gradualmente ambos lados. Pero es crucial que entiendas que podemos tener un TRIÁNGULO SIMÉTRICO o uno ASIMÉTRICO. Esto depende de si el punto de salida está en una posición desplazada igualmente entre los extremos, tendremos la creación de un triángulo simétrico. Si el punto de cierre o salida está muy cerca de uno de los extremos, el triángulo será asimétrico. Para lograr esto, utilizaremos una suma y una resta alternas. Esto se hace en estos puntos específicamente. La forma de alternar estos puntos es probando el valor de reducción actual.

Con esto, obtendremos el gráfico final muy parecido al de la figura 10. Se muestra a continuación:

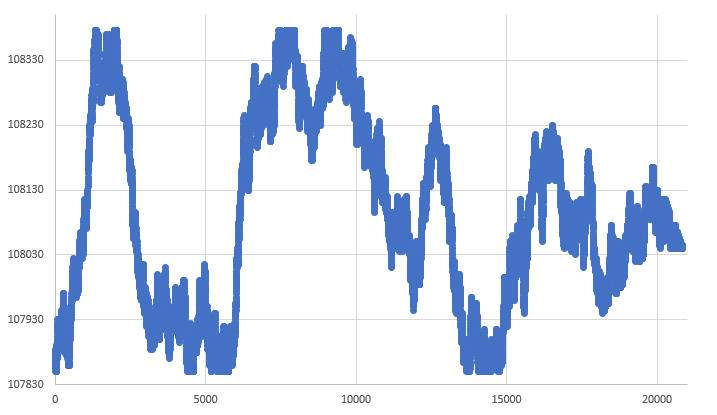
Figura 10 - Gráfico del Random Walk de una barra de 1 minuto

Observa que parece mucho más natural que cualquier otro gráfico visto anteriormente. Con esto, cerramos la base del random walk. Y podremos avanzar a las próximas etapas de nuestro sistema de repetición/simulación.

Para que puedas comprender cómo está actualmente el sistema.

En el anexo, tienes acceso al código completo y en su estado actual de desarrollo.

Conclusão

En realidad, no necesitas utilizar matemáticas extravagantes para explicar o crear cosas. Cuando se inventó la rueda, no se utilizó matemáticas para determinar cuál debía ser su radio basado en el valor correspondiente a PI. Todo lo que se hizo fue lograr que el movimiento deseado ocurriera. En este artículo, he demostrado que matemáticas simples, utilizadas en juguetes para niños, pueden explicar y representar movimientos que muchos creen imposibles de representar. Y siguen utilizando matemáticas extravagantes, cuando la solución es simple. Así que siempre busca hacer lo simple.