
Algoritmi di ottimizzazione della popolazione: Algoritmo di Ottimizzazione del Cuculo (COA)
Contenuto
1. Introduzione2. Descrizione dell'algoritmo, albero decisionale e volo di Levy
3. Codice COA
4. Risultati del test
1. Introduzione
Il cuculo è un uccello affascinante, non solo per il suo canto, ma anche per la sua strategia di riproduzione aggressiva, che consiste nel deporre le uova nei nidi di altri uccelli. In questo modo, l'uccello trasferisce completamente le proprie responsabilità genitoriali ad altre specie. Ogni specie di cuculo depone uova di un certo colore e di una certa dimensione, per adattarsi al meglio alle uova dei vari genitori adottivi. I pulcini di cuculo gettati nei nidi di altri uccelli sono di solito più grandi e più forti dei pulcini dei proprietari del nido, quindi i cuculi hanno bisogno di più cibo. Durante lo sviluppo, i pulcini di cuculo di Hodgson sviluppano un disegno speciale sulle loro ali a forma di becco aperto, che consente loro di ricevere più cibo dai genitori adottivi. Il cuculo non è l'unico uccello a mostrare questa caratteristica. Il parassitismo dei nidi è stato riscontrato in almeno 80 specie di uccelli. Questo fenomeno è diffuso anche in alcune specie di insetti sociali - calabroni, api e formiche, le cui femmine penetrano in un'altra colonia, uccidono la regina e depongono le loro uova. Il parassitismo di nidificazione esiste anche tra alcuni pesci, come i pesci gatto del lago Tanganica in Africa, che gettano le loro uova ad altri pesci che incubano le uova nella loro bocca.
La ricerca del cuculo è uno dei più recenti algoritmi euristici ispirati alla natura, sviluppato da Yang e Deb nel 2009. Si basa sul parassitismo di alcune specie di cuculi. Questo algoritmo è stato ulteriormente migliorato con i cosiddetti voli di Levy piuttosto che con i semplici metodi isotropi delle passeggiate aleatorie.
2. Descrizione dell'algoritmo
Cuckoo Optimization Algorithm (COA) viene utilizzato per l'ottimizzazione continua non lineare. Il COA si ispira allo stile di vita di questo uccello. L'algoritmo di ottimizzazione si basa sulle caratteristiche della deposizione delle uova e della riproduzione della specie. Come altri approcci evolutivi, il COA inizia con una popolazione iniziale. La base dell'algoritmo è un tentativo di sopravvivenza. Mentre competono per la sopravvivenza, alcuni uccelli muoiono. I cuculi sopravvissuti si spostano in luoghi migliori e iniziano a riprodursi e a deporre le uova. Infine, i cuculi sopravvissuti convergono in modo tale da ottenere una società di cuculi con valori di fitness simili.
Il vantaggio principale di questo metodo è la sua semplicità: la ricerca del cuculo richiede solo quattro parametri comprensibili, quindi la messa a punto diventa un gioco da ragazzi.
Nell'algoritmo di ricerca del cuculo, le uova nel nido sono interpretate come possibili soluzioni al problema di ottimizzazione e l'uovo del cuculo rappresenta la nuova soluzione. L'obiettivo finale del metodo è quello di utilizzare queste nuove (e potenzialmente migliori) soluzioni di uova parassitarie di cuculo per sostituire l'attuale soluzione di uova del nido. Questa sostituzione, effettuata in modo iterativo, porta alla fine a una soluzione.
I professori Yang e Deb hanno proposto le seguenti tre serie di stati ideali per l'algoritmo:
1. Ogni cuculo depone un uovo e lo lascia cadere in un nido scelto a caso.
2. I nidi migliori, con uova di alta qualità, saranno trasmessi alle generazioni successive.
3. Il numero di nidi disponibili è fisso e il nido può rilevare un uovo estraneo con la probabilità 'pa'. In questo caso, l'uccello ospite può gettare via l'uovo o lasciare il nido e l'uovo morirà.
Per semplicità, la terza ipotesi può essere approssimata dalla frazione pa di n nidi. Per il problema di massimizzazione, la qualità o l'adeguatezza della soluzione può essere semplicemente proporzionale alla funzione obiettivo. Tuttavia, è possibile definire anche altre espressioni (più complesse) per la funzione di fitness.
Per ogni iterazione g, viene selezionato casualmente un uovo di cuculo e vengono generate nuove soluzioni xi (g + 1) utilizzando il volo di Levy, una sorta di passeggiata aleatoria in cui i passi sono determinati entro limiti di lunghezza dei passi che hanno una certa distribuzione di probabilità e le direzioni dei passi sono isotrope e casuali. Secondo i creatori originali del metodo, la strategia di utilizzare i voli di Levy è preferibile ad altre semplici passeggiate aleatorie, perché consente di ottenere prestazioni complessive migliori. L'equazione generale del volo di Levy è la seguente
xi(g + 1) = xi(g) + α ⊕ levy(λ),
dove g indica il numero della generazione corrente, mentre α > 0 indica la dimensione del passo, che dovrebbe essere correlata alla scala del particolare problema in esame. Il simbolo ⊕ viene utilizzato per indicare la moltiplicazione elementare. Notare che si tratta essenzialmente di una catena di Markov, poiché la posizione successiva nella generazione g + 1 dipende solo dalla posizione attuale nella generazione g e dalla probabilità di transizione data rispettivamente dal primo e dal secondo termine. Questa probabilità di transizione è modulata dalla distribuzione di Levy come:
levy(λ) ∼ g-λ, (1 < λ ≤ 3),
che ha varianza infinita con media infinita. La pratica ha dimostrato che i migliori risultati si ottengono con un grado fisso di 2.0. In questo caso, i passi formano essenzialmente un processo casuale con una distribuzione della lunghezza dei passi della legge di potenza a coda pesante. Dal punto di vista computazionale, la generazione di numeri casuali utilizzando i voli di Levy consiste in due fasi: prima si sceglie una direzione casuale secondo una distribuzione uniforme, poi si generano passi secondo la distribuzione di Levy scelta. L'algoritmo valuta quindi l'idoneità della nuova soluzione e la confronta con quella attuale. Se la nuova soluzione è più adatta, sostituisce quella attuale. D'altra parte, alcuni nidi vengono abbandonati (il proprietario del nido ha gettato l'uovo di cuculo o ha lasciato il nido e l'uovo è morto) per aumentare l'esplorazione dello spazio di ricerca alla ricerca di soluzioni più promettenti. Il tasso di sostituzione è determinato dalla probabilità di pa, un parametro del modello che deve essere regolato per migliorare le prestazioni. L'algoritmo viene applicato iterativamente fino a quando non viene soddisfatto il criterio di arresto. I criteri di terminazione più comuni sono che sia stata trovata una soluzione che soddisfa una soglia inferiore, che sia stato raggiunto un numero fisso di generazioni o che le iterazioni successive non producono risultati migliori.
Soffermiamoci più in dettaglio sul processo di deposizione delle uova da parte del cuculo. Tra tutti i nidi, verrà selezionato a caso quello in cui si suppone che venga deposto l'uovo. Poiché l'uovo è una soluzione, può essere rappresentato dalla qualità dell'uovo. Se l'uovo di cuculo è di qualità superiore a quello del genitore, viene sostituito. In caso contrario, l'uovo del genitore rimarrà nel nido. Infatti, l'evoluzione successiva continuerà a partire dal pulcino sopravvissuto. Ciò significa che se il pulcino dell'uovo madre è sopravvissuto, l'evoluzione continuerà dallo stesso punto. Un ulteriore sviluppo è possibile solo se l'uovo di cuculo risulta essere più praticabile e la ricerca della soluzione del problema continua da un nuovo posto. L'albero decisionale è schematicamente rappresentato nella Figura 1.
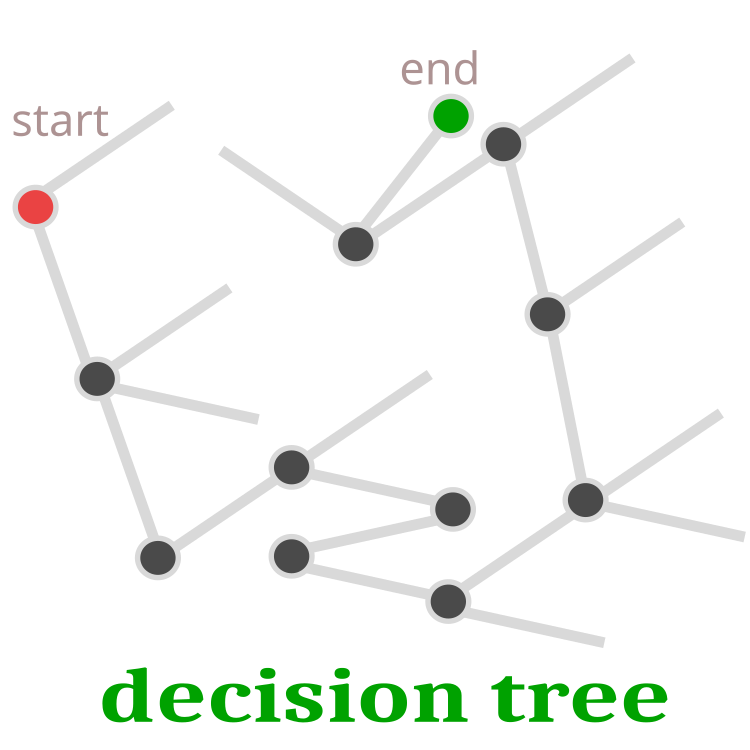
Fig. 1. Albero decisionale. Il punto rosso è l'inizio, il punto verde è la decisione finale.
Il secondo componente della base dell'algoritmo, dopo l'albero decisionale, è il volo di Levy. Il volo di Levy è una passeggiata aleatoria (un processo statistico di Markov) in cui la lunghezza del salto varia in passi, la direzione dei salti cambia in modo casuale e la distribuzione di probabilità è un caso speciale della distribuzione di Pareto ed è caratterizzata da code pesanti. È definito come un salto nello spazio e il salto è isotropo in direzioni casuali. Il volo di Levy è uno strumento per descrivere processi stocastici anomali. La dispersione è infinita (sono possibili salti di grandi lunghezze), le lunghezze dei salti sono autosimili a tutti i livelli (salti brevi sono intervallati da voli lunghi). Il termine volo di Levy viene talvolta esteso per includere una passeggiata aleatoria che si verifica su una griglia discreta piuttosto che in uno spazio continuo.
Una chiara applicazione del volo di Levy nell'algoritmo del cuculo può essere immaginato se consideriamo un problema di ottimizzazione con un parametro. Prendiamo una funzione ipotetica (la linea nera nella Figura 2), che non cambia per la maggior parte del suo dominio di definizione, cioè la linea orizzontale (y=x). Solo in una piccola area, la funzione cambia e ha un massimo. Se iniziamo la ricerca del massimo dal punto arancione della Figura 2, ottenendo poi un valore casuale x con la distribuzione di Levy, ci allontaneremo dal punto di partenza, pur non ottenendo una variazione della funzione. Tuttavia, con un forte salto nella coda della distribuzione, otteniamo un punto verde, che è una soluzione migliore di quella originale arancione, e quindi solo dal punto verde possiamo migliorare il risultato, avvicinandoci al massimo della funzione. In questo esempio, il volo di Levy migliora notevolmente la capacità di ricerca dell'algoritmo.
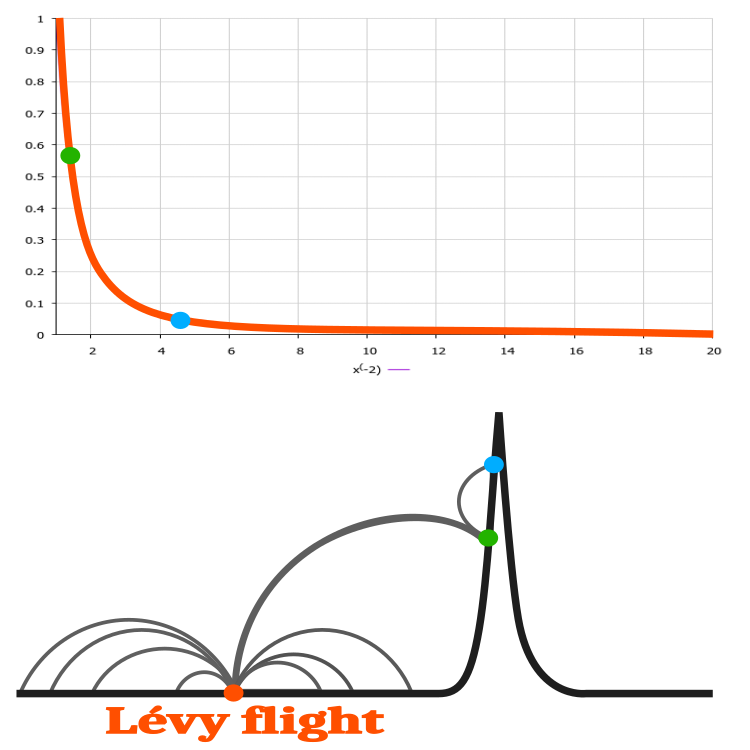
Figura 2. Un esempio di ricerca della soluzione di un'ipotetica funzione unidimensionale utilizzando il volo di Levy
Il concetto di volo Levy è utilizzato nella teoria del caos, quando si modellano fenomeni naturali casuali o pseudocasuali (ad esempio, il volo di un albatros, che combina traiettorie lunghe e brevi). Tra gli esempi vi sono l'analisi dei dati dei terremoti, la matematica finanziaria, la crittografia, l'analisi dei segnali, i moti turbolenti, oltre a numerose applicazioni in astronomia, biologia e fisica.
Pseudo codice dell'algoritmo COA (Figura 3):
1. Inizializzazione del cuculo con valori casuali.
2. Definire il fitness.
3. Depongono le uova in nidi casuali.
4. Svuotare il nido con una determinata probabilità.
5. Invia i cuculi dalla posizione corrente in una direzione casuale all'interno della distanza del volo di Levi.
6. Definire il fitness.
7. Depongono le uova in nidi casuali.
8. Svuotare il nido con una determinata probabilità.
9. Ripetere p. 5 fino a quando non viene soddisfatto il criterio di arresto.
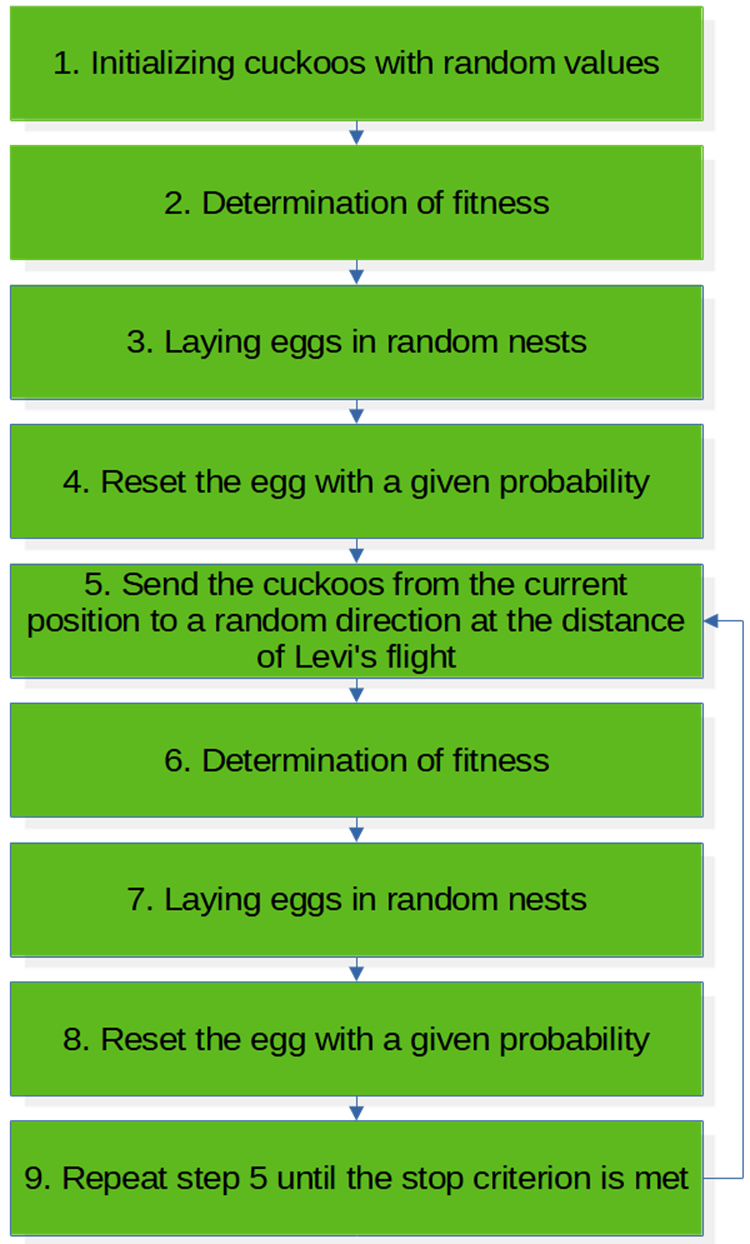
Fig. 3. Schema a blocchi dell'algoritmo COA
3. Codice COA
Cominciamo a considerare il codice dell'algoritmo. La soluzione al problema è il cuculo, che è anche l'uovo. Si tratta di una struttura semplice che include le coordinate nello spazio di ricerca e il valore della funzione di fitness (qualità delle uova).
//—————————————————————————————————————————————————————————————————————————————— struct S_Cuckoo { double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
Descriviamo il nido sotto forma di struttura. Qui, proprio come nella struttura di un uovo, ci sono le coordinate nello spazio e il valore della funzione di fitness. "Deporre l'uovo nel nido" significa essenzialmente copiare la struttura dell'uovo nella struttura del nido. Quando si utilizza il parametro probabilistico pa, l'uovo viene espulso dal nido quando un numero casuale da 0.0 a pa cade fuori l'intervallo [0.0;1.0] e il valore di e è impostato su -DBL_MAX.
//—————————————————————————————————————————————————————————————————————————————— struct S_Nest { void Init (int coordinates) { ArrayResize (c, coordinates); e = -DBL_MAX; } double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
Classe di algoritmi. Qui vengono dichiarati i metodi di inizializzazione pubblici, i due principali metodi di chiamata nel programma utente, gli intervalli dei valori degli argomenti del problema di ottimizzazione e ulteriori metodi privati che svolgono funzioni di servizio.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Cuckoo cuckoos []; //all the cuckoos public: double cB []; //best coordinates (egg parameters) public: double eB; //best eggs quality public: void Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP); //step control value public: void CuckooFlight (); public: void LayEggs (); //============================================================================ private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: S_Nest nests []; //nests private: int cuckoosNumber; //number of cuckoos private: int nestsNumber; //number of cuckoo nests private: double koef_pa; //probability of detection of cuckoo eggs private: double koef_alpha; //step control value private: double v []; private: int coordinates; //coordinates number private: bool clutchEggs; //clutch of eggs }; //——————————————————————————————————————————————————————————————————————————————
Init () metodo pubblico. Qui vengono azzerati i valori delle variabili e viene allocata la memoria per gli array.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP) //step control value { MathSrand (GetTickCount ()); clutchEggs = false; eB = -DBL_MAX; coordinates = coordinatesP; cuckoosNumber = cuckoosP; nestsNumber = nestsP; koef_pa = koef_paP; koef_alpha = koef_alphaP; ArrayResize (nests, nestsNumber); for (int i = 0; i < nestsNumber; i++) { nests [i].Init (coordinates); } ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (v, coordinates); ArrayResize (cuckoos, cuckoosNumber); for (int i = 0; i < cuckoosNumber; i++) { ArrayResize (cuckoos [i].c, coordinates); } } //——————————————————————————————————————————————————————————————————————————————
Il primo metodo pubblico chiamato a ogni iterazione del "volo del cuculo". Se il flag clutchEggs è disattivato, allora si inviano i cuculi in una direzione casuale, generando numeri casuali nell'intervallo della coordinata corrispondente. Se il flag è abilitato, il volo effettivo del cuculo viene effettuato in base alla distribuzione del volo Levy nell'intervallo del vettore v. Il vettore v viene precalcolato in Init () per ogni coordinata separatamente, poiché ogni coordinata può avere un intervallo di valori diverso.
L'espressione cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); significa che aggiungiamo lo scostamento r1 * v [c] * pow (r2, -2.0), dove r1 è -1 o 1, che determina la direzione dello scostamento dalla posizione originale, v è un vettore di dislocamento, r2 è un numero casuale nell'intervallo da 0.0 a 20.0 elevato a potenza -2.0. L'elevazione di un numero casuale a una potenza è la funzione del volo di Levy. Il suo grafico è riportato nella Figura 2.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::CuckooFlight () { //---------------------------------------------------------------------------- if (!clutchEggs) { for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } clutchEggs = true; } else { double r1 = 0.0; double r2 = 0.0; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; r2 = RNDfromCI (1.0, 20.0); cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Il secondo metodo pubblico chiamato a ogni iterazione è la "deposizione delle uova". In questo metodo, la simulazione della deposizione di un uovo di cuculo in un nido viene riprodotta algoritmicamente. Questo avviene scegliendo un nido a caso tra tutti quelli esistenti. Successivamente, si confronta la qualità dell'uovo di cuculo con quello già presente nel nido. Se l'uovo di cuculo è migliore, si procede alla sua sostituzione. Una caratteristica interessante dell'algoritmo in questo metodo è che la probabilità che l'uovo muoia viene eseguita dopo la deposizione anche se l'uovo di cuculo era più adatto. Ciò significa che c’è la possibilità koef_pa che qualsiasi uovo muoia, indipendentemente da ciò che vi si trova, proprio come in natura. Se l'uovo è morto o è stato buttato fuori dal nido, che di fatto è la stessa cosa, allora il nido sarà libero per una nuova deposizione di un uovo di qualsiasi fitness, anche inferiore, che algoritmicamente significa ricerca in un nuovo luogo.
In questo modo uno dei metodi dell'evoluzione naturale, come il parassitismo dei nidi, può essere descritto in poche righe di codice. Molti autori nelle loro pubblicazioni raccomandano di inizializzare il nido dopo la rimozione dell'uovo con nuovi valori casuali, il che significa iniziare la ricerca dall'inizio. Nella maggior parte dei casi, questo non darà il risultato desiderato in termini di aumento delle abilità esplorative dell'algoritmo. Le mie ricerche hanno dimostrato che è più conveniente lasciare semplicemente il nido vuoto e che uno dei cuculi vi deporrà un uovo, indipendentemente dalla qualità dell'uovo. È meglio dei valori casuali. La variabilità dello studio è data da salti casuali in direzioni casuali rispetto alle coordinate correnti. Di conseguenza, saranno necessarie meno iterazioni nella ricerca della soluzione migliore, aumentando così il tasso di convergenza dell'algoritmo nel suo complesso.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::LayEggs () { int ind = 0; //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ for (int i = 0; i < cuckoosNumber; i++) { ind = (int)round (RNDfromCI (0.0, nestsNumber - 1)); if (cuckoos [i].e > nests [ind].e) { nests [ind].e = cuckoos [i].e; ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY); if (cuckoos [i].e > eB) { eB = cuckoos [i].e; ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY); } } else { ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY); } } //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv for (int n = 0; n < nestsNumber; n++) { if (RNDfromCI (0.0, 1.0) < koef_pa) { nests [ind].e = -DBL_MAX; } } } //——————————————————————————————————————————————————————————————————————————————
4. Risultati del test
Ecco i risultati del test:
2022.11.30 11:31:54.490 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) 1 Skin's; Func cicli 10000 risultato: 4.918379100238852
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) Punteggio: 1.00000
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) 20 Skin's; Func cicli 10000 risultato: 4.257477577760983
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.84220
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) 500 Skin's; Func cicli 10000 risultato: 1.3521208312080903
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.14849
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) 1 Forest's; Func cicli 10000 risultato: 1.7600394018343262
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.99557
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) 20 Forest’s; Func cicli 10000 risultato: 0.4968964923017033
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.28107
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) 500 Forest’s; Func cicli 10000 risultato: 0.07638950254648778
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.04321
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) 1 Megacity's; Func cicli 10000 risultato: 12.0
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) Punteggio: 1.00000
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) 20 Megacity's; Func cicli 10000 risultato: 2.69
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.22417
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) 500 Megacity's; Func cicli 10000 risultato: 0.40800000000000003
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) Punteggio: 0.03400
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) Tutti i punteggi per C_AO_COA: 0.507633670637353
L'algoritmo di ricerca Levy flight cuckoo ha mostrato risultati impressionanti. Nella maggior parte dei test, ha superato gli altri algoritmi di ottimizzazione. In particolare, l'algoritmo ha mostrato una convergenza del 100% sulla funzione regolare Skin a due variabili e sulla funzione discreta Megacity a due variabili. Ciò che è ancora più sorprendente è che ha mostrato un'eccellente scalabilità su una funzione discreta. In altri test, è solo leggermente inferiore all'algoritmo della colonia di formiche. Al momento, abbiamo un leader indiscusso nella classifica di rating.
Vorrei chiarire che tutti gli algoritmi hanno parametri di regolazione che influiscono sui risultati finali in una misura o nell'altra, quindi è possibile che alcuni di questi algoritmi abbiano parametri ancor più ottimali e che la tabella di valutazione abbia un aspetto diverso. Ho solo mostrato i risultati dei test con i parametri che ho trovato per garantire il miglior risultato. Se riuscite a trovare parametri migliori e a ottenere risultati superiori, allora posso correggere la tabella di valutazione sulla base di questi. Si presume che l'algoritmo della formica possa competere con successo con l'attuale leader, dal momento che in alcuni indicatori è in vantaggio rispetto all'algoritmo di ricerca del cuculo, mentre è minimamente indietro in termini di indicatori finali. GWO è ancora leader nella funzione Skin con 1000 variabili. In ogni caso, coloro che utilizzeranno gli algoritmi nei loro progetti per risolvere i problemi di ottimizzazione possono navigare nella tabella e scegliere un algoritmo per le loro esigenze specifiche.
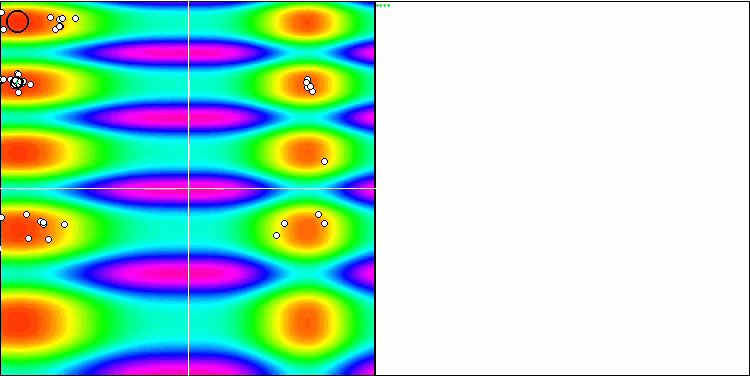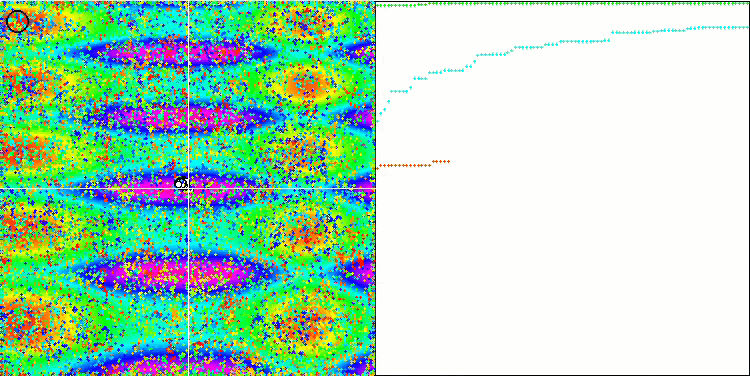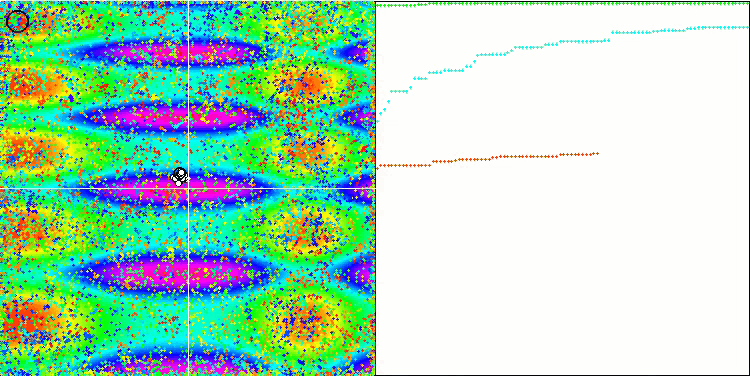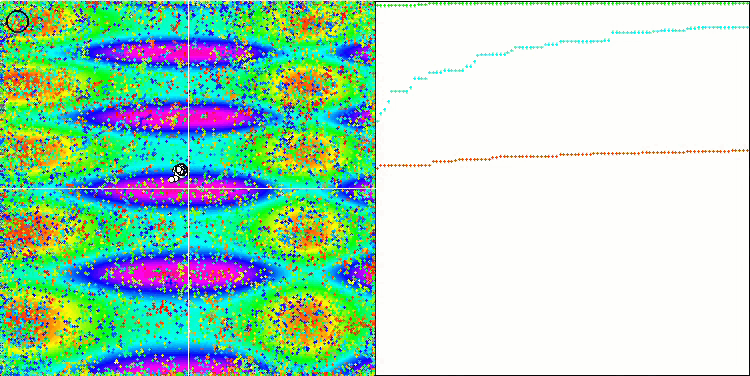
COA sulla funzione test Skin .
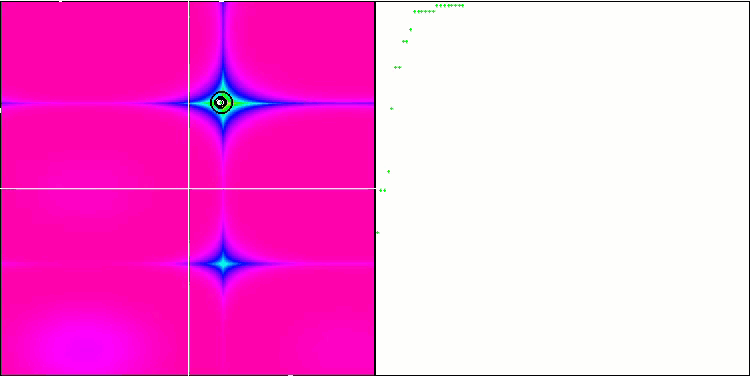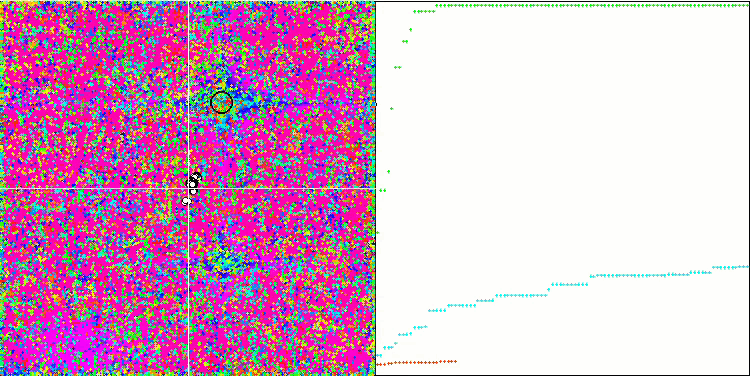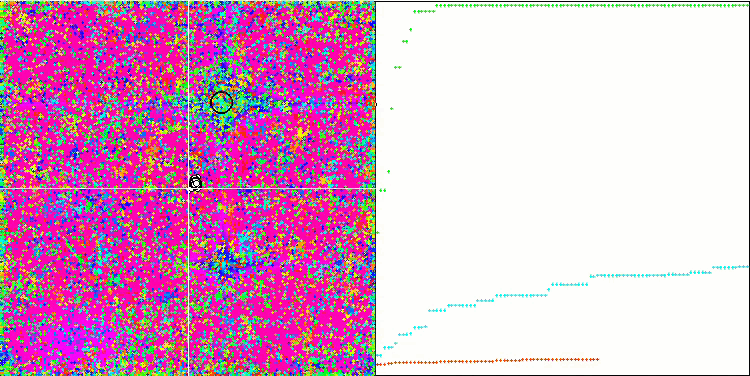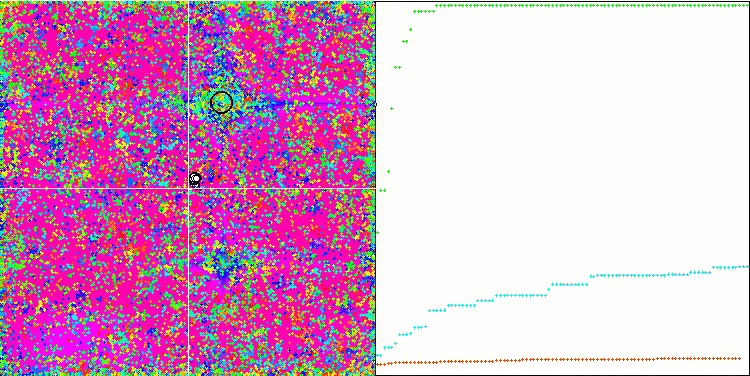
COA sulla funzione di test Forest .
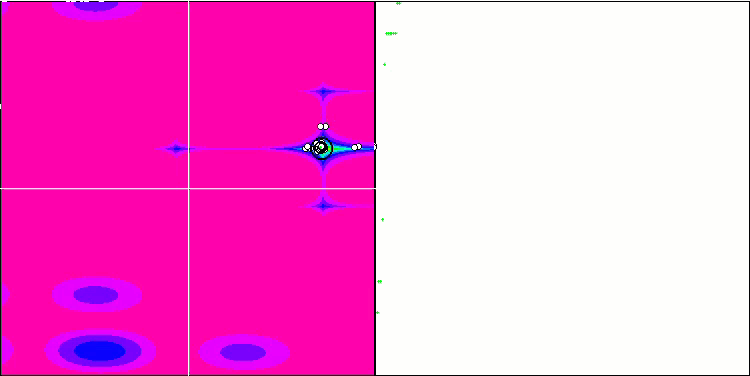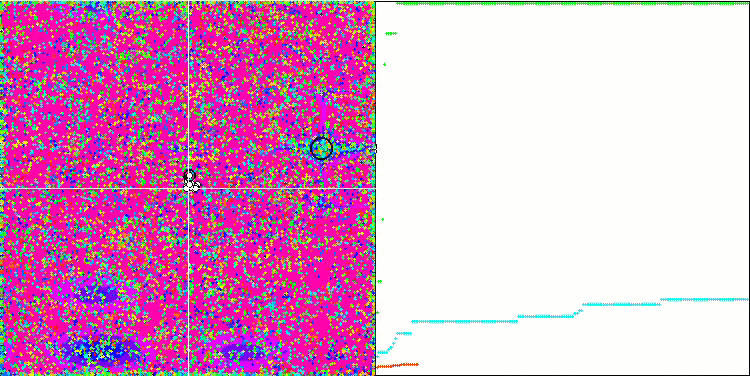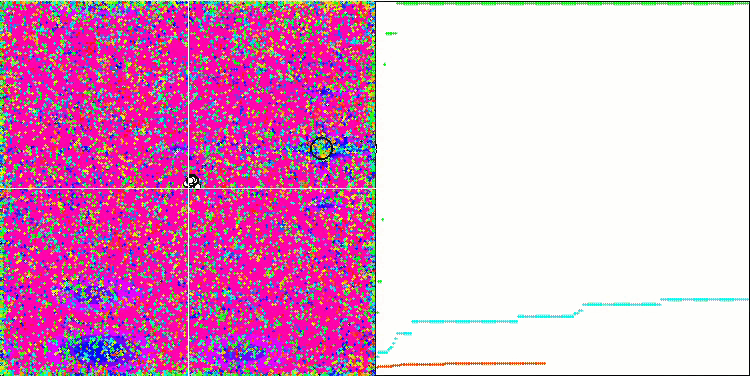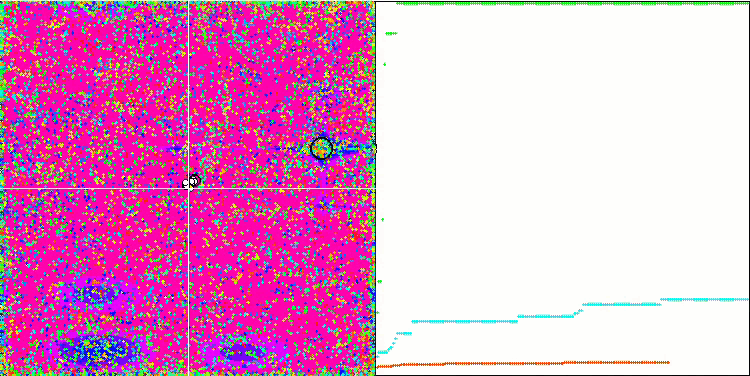
COA sulla funzione di test Megacity .
Sulla visualizzazione del banco di prova, il comportamento dell'algoritmo differisce da quelli considerati in precedenza, tuttavia, ci sono alcune caratteristiche che sono proprie degli algoritmi che suddividono il compito in aree di studio, come l'algoritmo della colonia di api. Ciò caratterizza la capacità dell'algoritmo di non concentrarsi su un singolo estremo, ma di esplorare diverse aree potenzialmente promettenti, fornendo all'algoritmo una resistenza contro il blocco negli estremi locali. A questo proposito, potrebbe essere possibile migliorare l'algoritmo ordinando i nidi e scegliendoli dal cuculo in proporzione alla loro qualità. Ciò significa che il cuculo sceglie i nidi, invece di mettere un uovo in un nido selezionato a caso, come nella versione canonica dell'algoritmo. Tuttavia, questo non ha migliorato i risultati, dimostrando la praticità della scelta casuale dei nidi. Forse questo ricorda ciò che accade in natura. Sostituire un uovo in caso di ospiti più intelligenti è più difficile, il che lo rende casuale e statisticamente ingiustificato.
Un'altra caratteristica dell'algoritmo è che si comporta come una passeggiata aleatoria su funzioni con molte variabili. Visivamente, sembra un rumore bianco o un vecchio schermo televisivo. Una certa concentrazione di coordinate nei punti di estremo locale si nota solo alla fine delle iterazioni. Vorrei fornire una "cristallizzazione" più chiara dei parametri, come nel caso dell'algoritmo della colonia di formiche. Siamo così giunti al problema generale di tutti gli algoritmi di ottimizzazione, che non ha una soluzione generale. Molti autori di algoritmi classici e abbastanza nuovi hanno cercato di risolverlo.
L'essenza del problema è la seguente: non si sa con certezza quale dei parametri ottimizzati della funzione oggetto di studio abbia priorità o forza, non si sa in che misura e come ciascuno dei parametri influisca sul risultato. Ad esempio, ci sono diversi parametri e l'algoritmo ha già trovato quello giusto, ma non si sa quale sia esattamente. L'algoritmo continuerà a cercare di cambiarli tutti, anche se è sufficiente cambiarne solo alcuni per raggiungere l'estremo globale. Il problema si aggrava quando si tratta di una funzione con molte decine o migliaia di variabili. Più sono le variabili, più il problema si aggrava. Visivamente, questo sembra un rumore bianco sullo schermo.
Ho fatto un tentativo per risolvere questo problema almeno in parte. Se non si conosce a priori quali parametri della funzione in esame debbano essere modificati e quali debbano rimanere invariati, possiamo provare a risolvere in modo probabilistico. Partiamo dal presupposto che solo una parte di tutti i parametri deve essere modificata e non tutti allo stesso tempo. L'algoritmo PSO si comporta in modo particolare. Con l'aumento del numero di parametri (argomenti) della funzione ottimizzata, questa si comporta come una nuvola che non ha la capacità di concentrarsi. A tale scopo, ho introdotto un nuovo parametro per l'algoritmo, che imposta la probabilità che la coordinata venga modificata, altrimenti viene lasciata invariata.
E il risultato è... Positivo!!! I risultati dei test sono migliorati. La "cristallizzazione" che volevo ottenere è apparsa su funzioni con molte variabili.
I risultati del banco di prova sono i seguenti:
2022.12.03 16:01:26.256 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) 1 Skin's; Func cicli 10000 risultato: 4.918367945334852
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) Punteggio: 1.00000
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) 20 Skin; Func cicli 10000 risultato: 4.328327964103814
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) Punteggio: 0.85911
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) 500 Skin; Func cicli 10000 risultato: 1.3297901702583084
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) Punteggio: 0.14316
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) 1 Forest's; Func cicli 10000 risultato: 1.755200932219688
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) Punteggio: 0.99283
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) 20 Forest’s; Func cicli 10000 risultato: 0.5089243656052672
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) Punteggio: 0.28787
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) 500 Forest’s; Func cicli 10000 risultato: 0.08044934398920801
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) Punteggio: 0.04551
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) 1 Megacity's; Func cicli 10000 risultato: 12.0
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) Punteggio: 1.00000
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) 20 Megacity's; Func cicli 10000 risultato: 2.9899999999999998
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) Punteggio: 0.24917
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) 500 Megacity's; Func cicli 10000 risultato: 0.4244
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) Punteggio: 0.03537
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) Tutti i punteggi per C_AO_COAm: 0.5125572342985216
La "cristallizzazione" è chiaramente visibile nella visualizzazione. Lo schermo, che a prima vista sembra un rumore bianco, viene cancellato, le coordinate iniziano a concentrarsi, i centri di concentrazione diventano mobili:

COAm sulla funzione di test Megacity . L'effetto di "cristallizzazione" è più visibile.
Da un lato c'è la variabilità, cioè la capacità di cercare dinamicamente nuove aree, mentre dall'altro la capacità di mettere a fuoco le coordinate degli estremi già raggiunti. Di seguito è riportata l'animazione dell'algoritmo della colonia di formiche con una "cristallizzazione" pronunciata per confronto:
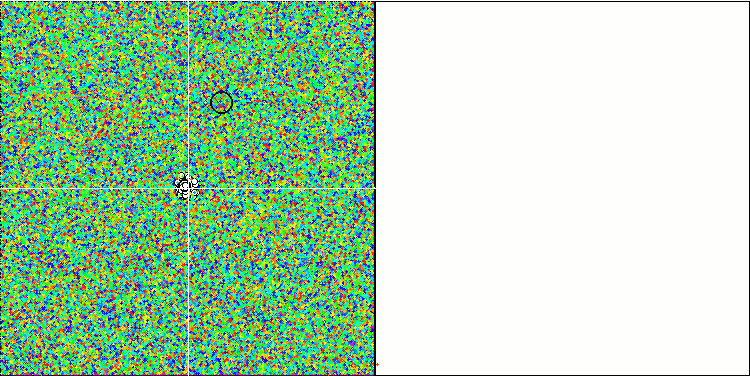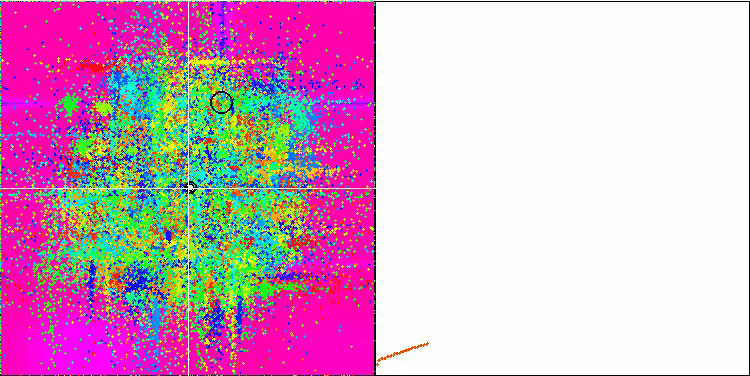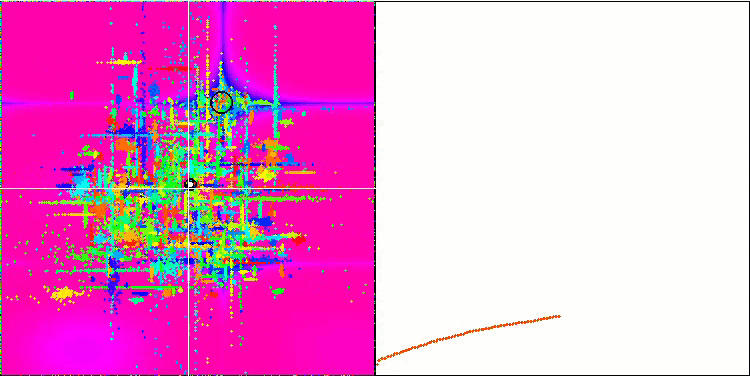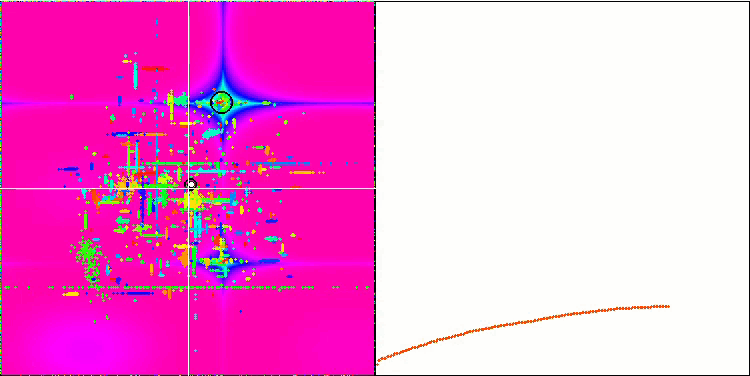
ACOm sulla funzione di test Forest .
Risultati del test
| AO | Descrizione | Skin | Forest | Megacity (discreta) | Risultato finale | ||||||
| 2 parametri (1 F) | 40 parametri (20 F) | 1000 parametri (500 F) | 2 parametri (1 F) | 40 parametri (20 F) | 1000 parametri (500 F) | 2 parametri (1 F) | 40 parametri (20 F) | 1000 parametri (500 F) | |||
| algoritmo di ottimizzazione del cuculo | 1.00000 | 0.85911 | 0.14316 | 0.99283 | 0.28787 | 0.04551 | 1.00000 | 0.24917 | 0.03537 | 0.51255778 | |
| ottimizzazione della colonia di formiche | 0.98229 | 0.79108 | 0.12602 | 1.00000 | 0.62077 | 0.11521 | 0.38333 | 0.44000 | 0.02377 | 0.49805222 | |
| colonia di api artificiali M | 1.00000 | 0.63922 | 0.08076 | 0.99908 | 0.20112 | 0.03785 | 1.00000 | 0.16333 | 0.02823 | 0.46106556 | |
| colonia di api artificiali | 0.99339 | 0.73381 | 0.11118 | 0.99934 | 0.21437 | 0.04215 | 0.85000 | 0.16833 | 0.03130 | 0.46043000 | |
| ottimizzazione del lupo grigio | 0.99900 | 0.48033 | 0.18924 | 0.83844 | 0.08755 | 0.02555 | 1.00000 | 0.10000 | 0.02187 | 0.41577556 | |
| ottimizzazione dello sciame di particelle | 0.99627 | 0.38080 | 0.05089 | 0.93772 | 0.14540 | 0.04856 | 1.00000 | 0.09333 | 0.02233 | 0.40836667 | |
| casuale | 0.99932 | 0.44276 | 0.06827 | 0.83126 | 0.11524 | 0.03048 | 0.83333 | 0.09000 | 0.02403 | 0.38163222 | |
Un vantaggio dell'algoritmo di ricerca del cuculo è che la sua ricerca globale utilizza voli o un processo Levy piuttosto che passeggiate aleatorie standard. Poiché i voli di Levy hanno media e varianza infinite, il COA può esplorare lo spazio di ricerca in modo più efficiente rispetto agli algoritmi di processo Gaussiano standard. Volo di Levy: un processo di passeggiata aleatoria caratterizzata da una serie di salti istantanei selezionati da una funzione di densità di probabilità con una legge di potenza a coda.
Al momento, l'algoritmo è il leader della tabella, superando in modo significativo gli altri algoritmi nei singoli test e rimanendo poco distante in altre "discipline". Ci sono risultati eccellenti sulla funzione discreta Megacity con 1000 argomenti che rendono la ricerca del cuculo un ottimo strumento per le attività dei trader (che sono discrete nella maggior parte dei casi). Risultati eccellenti (ma non i migliori) per la funzione Skin con 1000 argomenti danno ragione di affermare che l'algoritmo è adatto all'addestramento delle reti neurali in particolare e all'apprendimento automatico in generale.
Pro:
1. Alta velocità.
2. Versatilità. L'algoritmo può essere utilizzato in una varietà di problemi di ottimizzazione.
3. La capacità di non concentrarsi solo sugli estremi locali.
4. Alta convergenza per funzioni regolari e discrete.
5. Scalabile.
Contro:
1. Impostazioni multiple.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/11786
 Arriva il Nuovo MetaTrader 5 e MQL5
Arriva il Nuovo MetaTrader 5 e MQL5
 Utilizza i canali MQL5.community e le chat di gruppo
Utilizza i canali MQL5.community e le chat di gruppo
 Impara come progettare un sistema di trading tramite VIDYA
Impara come progettare un sistema di trading tramite VIDYA
- App di trading gratuite
- VPS Forex gratuito per 24 ore
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso