
Популяционные алгоритмы оптимизации: Тасующий алгоритм прыгающих лягушек (Shuffled Frog-Leaping, SFL)
Содержание:
1. Введение
2. Описание алгоритма
3. Результаты тестов
1. Введение
Тасующий алгоритм прыгающих лягушек (Shuffled Frog Leaping Algorithm, SFL) был предложен Юсуфом (М. Eusuff) и другими авторами в 2003 году. Этот алгоритм объединяет принципы меметического алгоритма и алгоритма роя частиц, и его разработка была вдохновлена поведением группы лягушек в процессе поиска пищи.
Изначально алгоритм SFL был разработан как метаэвристический метод для решения задач комбинаторной оптимизации. Он основан на использовании математических функций и информированного эвристического поиска.
Алгоритм SFL состоит из нескольких взаимодействующих виртуальных популяций лягушек, называемых мемплексами. Виртуальные лягушки выполняют роль хозяев или носителей мемов, где мем представляет собой единицу культурной эволюции. В каждом мемплексе происходит независимый локальный поиск с использованием метода, аналогичного оптимизации роя частиц, но с упором на локальный поиск.
Для обеспечения глобальных исследований виртуальные лягушки периодически перетасовываются и реорганизуются в новые мемплексы с помощью метода, аналогичного алгоритму перетасованной сложной эволюции. Кроме того, в популяции генерируются и заменяются случайные виртуальные лягушки, чтобы обеспечить возможность случайной генерации улучшенной информации.
Тасующий алгоритм прыгающих лягушек является эффективным методом для решения сложных задач оптимизации и позволяет достичь оптимальных решений в различных областях применения. В данной статье мы рассмотрим основные принципы и применение этого алгоритма, а также его преимущества и ограничения.
2. Описание алгоритма
Меметика (memetics) представляет собой подход к моделям эволюционной передачи информации, основанный на концепции мемов. Мемы, являющиеся аналогами генов, служат единицами культурной информации, распространяемой между людьми через имитацию, обучение и другие средства. Понятие мема было введено и основы меметики были разработаны Докинзом (C.R. Dawkins) в 1976 году. Мемы могут передаваться вертикально - от предшественников, родителей, воспитателей, книг, культурных артефактов и т.д. Также возможна горизонтальная передача мемов от человека к человеку и от культуры к культуре. Несмотря на то, что мемы представляют собой чистую информацию, их функционирование приводит к существенным изменениям поведения человека.
Меметические алгоритмы (Memetic algorithms, М-алгоритмы) определяются как гибридные популяционные метаэвристические алгоритмы поисковой оптимизации, основанные на концепции мема и неодарвиновском принципе эволюции. В контексте М-алгоритмов мем является реализацией алгоритма локальной оптимизации, уточняющего текущие решения на каждой итерации или через некоторое число итераций. М-алгоритмы можно рассматривать как гибридизацию одного из популяционных алгоритмов глобального поиска и одного или нескольких классических или популяционных алгоритмов локальной оптимизации. Первоначально М-алгоритмы были предложены как один из вариантов повышения эффективности генетических алгоритмов.
Эффективность М-алгоритмов в значительной степени зависит от значений их свободных параметров. В ряде исследований показано, что очень большое влияние на эффективность этих алгоритмов оказывает выбор используемых мемов. Поэтому данная проблема занимает одно из центральных мест в работах, посвященных М-алгоритмам.
Мемы представляют собой одну из революционных идей, подразумевающую схожесть эволюции генов и эволюции человеческой культуры. Докинз назвал единицу культурного обмена, аналог гена в культуре, мемом. Мемом можно назвать жест, слово или идею; любая единица культурной информации, которая может быть передана от человека к человеку посредством имитации обучения - это мем.
Меметические алгоритмы, в отличие от генетических, имитируют процесс культурной эволюции. Разработанный Москато подход использует аналогию с эволюцией мемов. Меметический алгоритм состоит из следующих этапов: локальный поиск, кооперация, соревнование, и критерий окончания поиска. Меметическим называют широкий класс алгоритмов, объединенных общей идеей: включением в генетический алгоритм индивидуального обучения особей и использование информации о структуре пространства возможных решений. Проблема баланса между популяционным и локальным поиском можно рассматривать как общую проблему соблюдения баланса между экстенсивными и интенсивными исследованиями пространства поиска.
Меметический алгоритм в общих чертах включает в себя следующие компоненты:
1. Локальный поиск. Для его осуществления можно использовать алгоритм имитации отжига и алгоритмы подъема.
2. Кооперация. Обмен информацией между особями может осуществляться через процедуру, аналогичную применению оператора двухточечного скрещивания в генетических алгоритмах.
3. Соревнование. Процедура селекции аналогична таковой в генетических алгоритмах и обычно заключается в отборе наиболее приспособленных особей в популяции и исключении из нее менее приспособленных.
4. Критерий окончания поиска. В меметических алгоритмах он может включать оценку разнообразия особей, помимо подсчета числа итераций и оценки улучшения результата.
Меметические алгоритмы - это широкий класс алгоритмов, объединенных общей идеей индивидуального обучения особей и использования информации о структуре пространства возможных решений.
Мемы, подобно генам, являются репликаторами, то есть объектами, способными к самовоспроизведению. Для мемов выживание и воспроизводство зависят от наличия носителя, который распространяет мем. Мемы могут видоизменяться, формируя новые мемы, и участвуют в борьбе за ресурсы - умы людей.
Мемы часто объединяются в комплексы, или мемплексы, для усиления в борьбе за носителей. Мемплексы аналогичны симбиотическим совокупностям генов, составляющих генетические коды биологических организмов. Примером мемплекса может быть религия. Мемплексы оказывают глубокое влияние на формирование индивидуального и общественного поведения.
Переходим непосредственно к тасующему алгоритму прыгающих лягушек. Основная идея алгоритма заключается в разбиении всей популяции лягушек с глобальным лидером G на мемы - группы, в каждой из которых есть лидер L (рисунок 1).

Рисунок 1. Популяция лягушек с глобальным лидером (G), разбитая на мемы со своим локальным лидером (L).
В рамках каждого мема лягушки стремятся двигаться в направлении локального лидера. Лидерство обновляется, если позиция одной из лягушек улучшается. Мемы не разделяются в пространстве поиска и могут иметь пересечения. Таким образом, лягушка, находящаяся на территории одного мема, вполне может принадлежать к другому. Это создает динамичную среду, где лягушки могут переходить пространственно из одного мема в другой, в зависимости от изменения их позиций в пространстве поиска.
Рассматриваем задачу глобальной условной оптимизации, в которой фитнес-функция подлежит максимизации. Алгоритм SFL включает в себя следующие основные шаги.
1.0 Инициализация алгоритма
1.1 Создание начальной популяции лягушек с случайными координатами.
1.2 Определение приспособленности каждой лягушки.
1.3 Создание мемплексов (подпопуляций), распределение лягушек по мемплексам.
2.0 Цикл поиска оптимального решения
2.1 Для каждого мемплекса:
2.1.1 Определить лучшую лягушку.
2.1.2 Переместить остальные лягушки в сторону лучшей лягушки в мемплексе.
2.2 Если перемещение лягушки не улучшило ее приспособленность:
2.2.1 Переместить ее в сторону глобально лучшей лягушки.
2.2.2 Если и это не улучшило приспособленность, переместить лягушку в случайное место на поле.
3.0 Измерение приспособленности лягушек
3.1 Для каждой лягушки в популяции измерить ее приспособленность.
3.2 Обновить информацию о лучшей лягушке в каждом мемплексе и в популяции в целом.
4.0 Определение глобально лучшей лягушки и обновление мемплексов
4.1 Определить глобально лучшую лягушку по всей популяции.
4.2 Если это последний цикл:
4.2.1 Сбросить счетчик циклов мемплекса.
4.2.2 Сгенерировать случайные индексы для лягушек.
4.2.3 Скопировать лягушек в мемплексы по новым индексам.
4.2.4 Определить в каждом мемплексе лучшую лягушку.
4.2.5 Сбросить приспособленность лягушек и шаг.
4.3 Если это не последний цикл:
4.3.1 Скопировать приспособленность и координаты лягушек из популяции в соответствующие лягушки мемплексов.
4.3.2 Определить в каждом мемплексе лучшую лягушку.
4.3.3 Определить направление следующего прыжка для каждой лягушки в зависимости от ее приспособленности.
Таким образом, основой алгоритма SFL является комбинирование локального поиска в пределах каждого из мемеплексов и глобального поиска путем обмена информацией о положениях лучших агентов мемеплексов.
Данный алгоритм представляет собой модификацию алгоритма SFL, в котором на этапе локального поиска агент движется не точно в направлении лучшего агента соответствующего мемеплекса, а в некотором случайным образом возмущенном направлении. Известны как последовательные, так и параллельные гибридизации алгоритма со многими популяционными алгоритмами, например с алгоритмом искусственной иммунной системы.
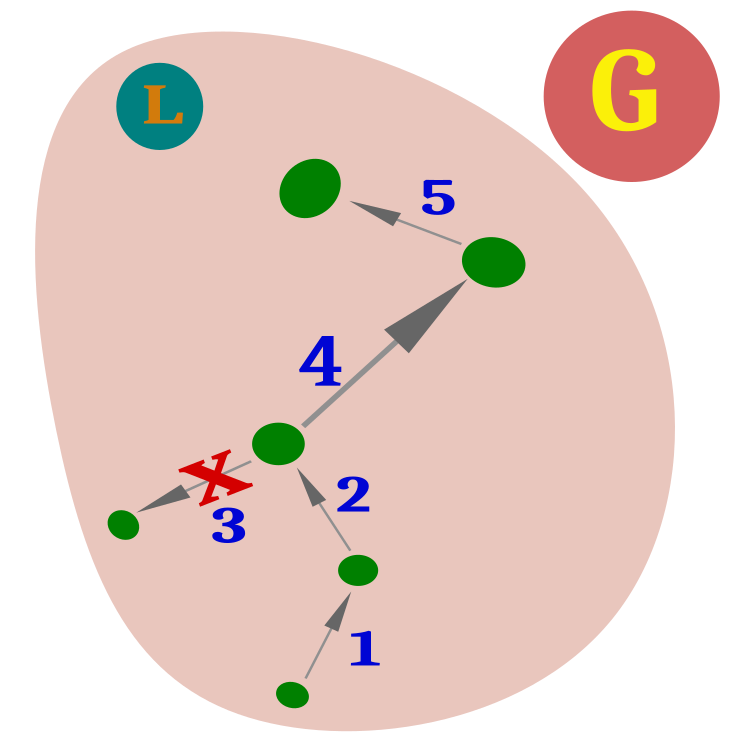
Рисунок 2. Прыжки лягушек. Если предыдущее перемещение оказалось неудачным, то следующий прыжок будет произведен из того же самого места.
Логической единицей алгоритма оптимизации SFL является лягушка, она может быть описана структурой S_Frog, которая представляет собой агента в пространстве поиска.
Структура S_Frog содержит следующие поля:
- c - массив координат текущей позиции лягушки.
- cPrev - массив координат предыдущей позиции лягушки.
- f - значение функции приспособленности для текущей позиции лягушки.
- fPrev - значение функции приспособленности для предыдущей позиции лягушки.
- frogStep - номер шага, на котором находится лягушка.
//—————————————————————————————————————————————————————————————————————————————— struct S_Frog { void Init (int coords) { ArrayResize (c, coords); ArrayResize (cPrev, coords); f = -DBL_MAX; fPrev = -DBL_MAX; frogStep = 0; } double c []; //coordinates double cPrev []; //previous coordinates double f; //fitness double fPrev; //previous fitness int frogStep; //frog step }; //——————————————————————————————————————————————————————————————————————————————
Структура S_Memeplex описывает мемплекс в алгоритме. Она содержит следующие поля:
- frogs - массив лягушек, составляющих мемплекс.
- fBest - лучшее значение функции приспособленности среди всех лягушек в мемплексе.
- cBest - массив координат, соответствующих лучшему значению функции приспособленности в мемплексе.
//—————————————————————————————————————————————————————————————————————————————— struct S_Memeplex { S_Frog frogs []; double fBest; //best fitness double cBest []; //best coordinates }; //——————————————————————————————————————————————————————————————————————————————
Класс C_AO_SFL предоставляет методы для инициализации алгоритма, перемещения лягушек и ревизии популяции. Он также содержит вспомогательные методы для преобразования значений и генерации случайных чисел.
Напишем класс алгоритма SFL, включающий в себя поля:
- cB - массив, хранящий лучшие координаты (best coordinates);
- fB - переменная, хранящая значение целевой функции (fitness function) для лучших координат;
- frogs - массив, хранящий всех лягушек в популяции;
- mems - массив, хранящий мемплексы (группы лягушек);
- rangeMax - массив, хранящий максимальные значения для каждой координаты поиска;
- rangeMin - массив, хранящий минимальные значения для каждой координаты поиска;
- rangeStep - массив, хранящий шаги поиска для каждой координаты.
Открытые методы класса:
- Init - метод инициализации параметров алгоритма, принимает следующие параметры:
- coordinatesNumberP - количество координат поиска;
- populationSizeP - размер популяции (количество лягушек);
- numbMemsP - количество мемплексов (групп лягушек);
- numbCyclesP - количество циклов в мемплексе;
- frogStepsToLocalMaxP - количество шагов лягушки до локального максимума;
- movConstantP - константа перемещения (шаг поиска) лягушек.
Moving - метод, реализующий перемещение лягушек в пространстве поиска.
Revision - метод, реализующий ревизию популяции лягушек и обновление лучших координат.
SeInDiSp - вспомогательный метод, реализующий преобразование значения из одного диапазона в другой с заданным шагом.
RNDfromCI - вспомогательный метод, генерирующий случайное число в заданном интервале.
Описание приватных полей класса:
- coordinatesNumber - количество координат поиска;
- frogsNumber - количество лягушек в популяции;
- numbMems - количество мемплексов (групп лягушек);
- numbCycles - количество циклов в мемплексе;
- frogStepsToLocalMax - количество шагов лягушки до локального максимума;
- movConstant - константа перемещения (шаг поиска) лягушек;
- memsFrogs - количество лягушек в каждом мемплексе;
- numbCyclesCNT - счетчик циклов;
- vect - массив, хранящий вектор;
- indexes - массив, хранящий индексы;
- revision - флаг, указывающий на необходимость ревизии популяции.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_SFL { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Frog frogs []; //all frogs public: S_Memeplex mems []; //memeplexes public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordinatesNumberP, //coordinates number const int populationSizeP, //population size const int numbMemsP, //number of memeplexes const int numbCyclesP, //number of cycles in the memeplex const int frogStepsToLocalMaxP, //frog steps to the local maximum const double movConstantP); //movement step (0.0 .. 1.0) public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coordinatesNumber; //coordinates number private: int frogsNumber; //frogs number private: int numbMems; //number of memeplexes private: int numbCycles; //number of cycles in the memeplex private: int frogStepsToLocalMax; //frog steps to the local maximum private: double movConstant; //movement step (0.0 .. 1.0) private: int memsFrogs; //number of frogs in the memplex private: int numbCyclesCNT; //cycle counter private: double vect []; //vector private: int indexes []; //indexes private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
Для инициализации алгоритма будем использовать метод инициализации Init, имеющий несколько параметров:
- coordinatesNumberP - количество координат
- populationSizeP - размер популяции
- numbMemsP - количество мемплексов
- numbCyclesP - количество циклов в мемплексе
- frogStepsToLocalMaxP - количество шагов лягушки до локального максимума
- movConstantP - шаг перемещения (от 0.0 до 1.0)
Вначале метод сбрасывает генератор случайных чисел и устанавливает начальное значение переменной fB (-DBL_MAX) и revision (false).
Затем метод создает массивы rangeMax, rangeMin, rangeStep, vect, indexes, cB, frogs и mems с нужными размерами.
Метод инициализирует каждую лягушку в массиве frogs и каждую лягушку в каждом мемплексе в массиве mems с помощью метода Init, передавая количество координат.
Затем метод устанавливает начальное значение переменной fBest каждого мемплекса в -DBL_MAX и создает массив cBest для каждого мемплекса с нужным размером.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SFL::Init (const int coordinatesNumberP, //coordinates number const int populationSizeP, //population size const int numbMemsP, //number of memeplexes const int numbCyclesP, //number of cycles in the memeplex const int frogStepsToLocalMaxP, //frog steps to the local maximum const double movConstantP) //movement step (0.0 .. 1.0) { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coordinatesNumber = coordinatesNumberP; frogsNumber = populationSizeP; numbMems = numbMemsP; numbCycles = numbCyclesP; frogStepsToLocalMax = frogStepsToLocalMaxP; movConstant = movConstantP; memsFrogs = frogsNumber / numbMems; numbCyclesCNT = 0; ArrayResize (rangeMax, coordinatesNumber); ArrayResize (rangeMin, coordinatesNumber); ArrayResize (rangeStep, coordinatesNumber); ArrayResize (vect, coordinatesNumber); ArrayResize (indexes, frogsNumber); ArrayResize (cB, coordinatesNumber); ArrayResize (frogs, frogsNumber); for (int i = 0; i < frogsNumber; i++) { frogs [i].Init (coordinatesNumber); } ArrayResize (mems, numbMems); for (int i = 0; i < numbMems; i++) { ArrayResize (mems [i].frogs, memsFrogs); for (int frgs = 0; frgs < memsFrogs; frgs++) { mems [i].frogs [frgs].Init (coordinatesNumber); } mems [i].fBest = -DBL_MAX; ArrayResize (mems [i].cBest, coordinatesNumber); } } //——————————————————————————————————————————————————————————————————————————————
Метод Moving предназначен для перемещения лягушек по пространству поиска. Метод достаточно большой и разберём его частями.
В начале кода проверяется значение переменной revision. Если оно равно false, то выполняется следующий блок кода:
- Задается начальное значение переменной fB, которая представляет собой наилучшую оценку функции. В данном случае ей присваивается значение -DBL_MAX (отрицательная бесконечность).
- Запускается цикл, в котором происходит инициализация каждой лягушки. Для каждой лягушки:
- Запускается цикл по каждой координате c.
- Генерируется случайное значение для координаты c с помощью функции RNDfromCI, которая возвращает случайное число в заданном диапазоне.
- Значение координаты c приводится к диапазону с помощью функции SeInDiSp, которая позволяет сдвинуть значение внутри диапазона с определенным шагом.
- Значение функции f для лягушки устанавливается равным -DBL_MAX.
- Значение предыдущего значения функции fPrev для лягушки устанавливается равным -DBL_MAX.
- Шаг лягушки frogStep устанавливается равным 0.
- Запускается цикл по каждой координате c.
- Вычисляется значение vect[c], которое представляет собой произведение разности между максимальным и минимальным значением диапазона на movConstant.
- Переменной revision присваивается значение true, чтобы указать, что инициализация была выполнена.
- Переменной numbCyclesCNT присваивается значение 0.
Таким образом, данный код выполняет инициализацию лягушек, устанавливает начальные значения функции и других параметров, а также вычисляет значение vect[c] для каждой координаты c.
if (!revision) { fB = -DBL_MAX; for (int frgs = 0; frgs < frogsNumber; frgs++) { for (int c = 0; c < coordinatesNumber; c++) { frogs [frgs].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); frogs [frgs].c [c] = SeInDiSp (frogs [frgs].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); frogs [frgs].f = -DBL_MAX; frogs [frgs].fPrev = -DBL_MAX; frogs [frgs].frogStep = 0; } } for (int c = 0; c < coordinatesNumber; c++) { vect [c] = (rangeMax [c] - rangeMin [c]) * movConstant; } revision = true; numbCyclesCNT = 0; }
Если флаг revision равен true, это означает, что алгоритм перешел в стадию перемещения лягушек. С переменными метода мы уже познакомились, поэтому подробно останавливаться на них не будем. В этой части кода реализуются прыжки лягушек в соответствии с индивидуальным для каждой лягушки шагом. На первом шаге лягушка прыгает в сторону локального лидера, попытка засчитывается, если положение лягушки стало лучше, в противном случае счетчик шага будет увеличен. То есть, на прыжки в сторону локального лидера выделяется фиксированное количество попыток согласно внешним параметрам алгоритма.
Для лягушки - лидера используется иной принцип перемещения в отличии от всех остальных в мемплексе. Лидер просто совершает прыжки в случайном направлении в небольшой окрестности своего положения.
В отличии от лидера все остальные лягушки совершают прыжки в сторону лидера по следующей формуле:
из формулы видим, что новая координата лягушки будет получена путём перемещения в сторону лидера на расстояние между ними, нормированное на евклидово расстояние по всем координатам, при этом вводится случайная компонента rnd.coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);
else { int cnt = 0; double eDistance = 0.0; //euclidean distance double coordDiff = 0.0; //the difference in coordinates for (int m = 0; m < numbMems; m++) { for (int frgs = 0; frgs < memsFrogs; frgs++) { //2.1 передвинуть лягушки в сторону лучшего в мемплексе----------------- if (mems [m].frogs [frgs].frogStep < frogStepsToLocalMax) { if (mems [m].frogs [frgs].fPrev != -DBL_MAX && mems [m].fBest != -DBL_MAX) { if (mems [m].frogs [frgs].fPrev == mems [m].fBest) { for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd; coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * 0.2; mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } else { eDistance = 0.0; coordDiff = 0.0; //посчитаем евклидово расстояние---------------------------------- for (int c = 0; c < coordinatesNumber; c++) { coordDiff = mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]; coordDiff *= coordDiff; eDistance += coordDiff; } eDistance = sqrt (eDistance); for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance); mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } } else { for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd; coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c]; mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } } else { //2.2 передвинуть в сторону глобального если ход хуже предыдущего----- if (mems [m].frogs [frgs].frogStep /*==*/ >= frogStepsToLocalMax) { eDistance = 0.0; coordDiff = 0.0; //посчитаем евклидово расстояние------------------------------------ for (int c = 0; c < coordinatesNumber; c++) { coordDiff = cB [c] - mems [m].frogs [frgs].cPrev [c]; coordDiff *= coordDiff; eDistance += coordDiff; } eDistance = sqrt (eDistance); for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((cB [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance); mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } //2.3 передвинуть случайно по полю -------------------------------- else { for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); coord = RNDfromCI (rangeMin [c], rangeMax [c]); mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } } frogs [cnt] = mems [m].frogs [frgs]; cnt++; } } //-------------------------------------------------------------------------- numbCyclesCNT++; }
Метод Revision предназначен для определения глобального лидера на каждой итерации алгоритма и определения локальных лидеров. Если количество циклов, отведённых на перемещения лягушек в рамках каждого мемплекса, исчерпано, то производим тасование - переназначаем лягушки по мемплексам случайным образом, тем самым осуществляется обмен информацией между мемплексами. В этом методе так же производится учет соответствующих шагов прыжков - куда будет перемещаться лягушка на следующей итерации (в сторону локального или глобального лидера или в случайном направлении в пространстве поиска).
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SFL::Revision () { //4.1 определить глобально лучшего по популяции------------------------------- for (int i = 0; i < frogsNumber; i++) { if (frogs [i].f > fB) { fB = frogs [i].f; ArrayCopy (cB, frogs [i].c, 0, 0, WHOLE_ARRAY); } } int cnt = 0; //если последний цикл========================================================= if (numbCyclesCNT >= numbCycles) { //4.2.0 сбросить счетчик циклов мемплекса----------------------------------- numbCyclesCNT = 0; //4.2.1 сгенерировать случайно индексы-------------------------------------- for (int i = 0; i < frogsNumber; i++) indexes [i] = i; Shuffle (indexes, frogsNumber); //4.2.2 скопировать случайно в мемплексы------------------------------------ for (int m = 0; m < numbMems; m++) { mems [m].fBest = -DBL_MAX; for (int frgs = 0; frgs < memsFrogs; frgs++) { mems [m].frogs [frgs] = frogs [indexes [cnt]]; cnt++; //4.2.3 определить в каждом мемплексе лучшего--------------------------- if (mems [m].frogs [frgs].f > mems [m].fBest) { mems [m].fBest = mems [m].frogs [frgs].f; ArrayCopy (mems [m].cBest, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY); } //4.2.4 сбросить приспособленность лягушек и шаг------------------------ mems [m].frogs [frgs].f = -DBL_MAX; mems [m].frogs [frgs].fPrev = -DBL_MAX; mems [m].frogs [frgs].frogStep = 0; } } } //если НЕ последний цикл====================================================== else { for (int m = 0; m < numbMems; m++) { for (int frgs = 0; frgs < memsFrogs; frgs++) { mems [m].frogs [frgs].frogStep++; //4.3.1 скопировать приспособленность и координаты лягушек из популяции в //соответствующие лягушки мемплексов mems [m].frogs [frgs].f = frogs [cnt].f; ArrayCopy (mems [m].frogs [frgs].c, frogs [cnt].c, 0, 0, WHOLE_ARRAY); //4.3.2 определить в каждом мемплексе лучшего--------------------------- if (frogs [cnt].f > mems [m].fBest) { mems [m].fBest = frogs [cnt].f; ArrayCopy (mems [m].cBest, frogs [cnt].c, 0, 0, WHOLE_ARRAY); } //4.3.3 определить направление следующего прыжка------------------------ if (mems [m].frogs [frgs].frogStep <= frogStepsToLocalMax) { if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev) { mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f; ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY); mems [m].frogs [frgs].frogStep = 0; } } else { if (mems [m].frogs [frgs].frogStep >= frogStepsToLocalMax + 1) { if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev) { mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f; ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY); mems [m].frogs [frgs].frogStep = 0; } } else { mems [m].frogs [frgs].f = -DBL_MAX; mems [m].frogs [frgs].fPrev = -DBL_MAX; mems [m].frogs [frgs].frogStep = 0; } } cnt++; } } } } //——————————————————————————————————————————————————————————————————————————————
В алгоритме оптимизации SFL нам понадобится перемешивать лягушки между мемплексами случайным образом. Задача случайного тасования интересна тем, что ее алгоритмическое решение нетривиально, однако благодаря Рональду Фишеру и Фрэнку Йетсу, мир получил эффективный и быстрый алгоритм. Ранее в статьях мы не использовали подобную концепцию, так как не было необходимости в этом. Он широко используется в компьютерных науках, особенно в области генетических алгоритмов, криптографии и статистики.
Основные преимущества алгоритма Фишера — Йетса:
1. Простота реализации: Алгоритм Фишера — Йетса легко реализовать на любом языке программирования. Он не требует сложных математических вычислений или специальных библиотек.
2. Эффективность: Алгоритм Фишера — Йетса работает за линейное время, то есть время выполнения зависит от количества элементов, которые нужно переставить. Это делает его очень эффективным для больших наборов данных.
3. Случайность: Алгоритм Фишера — Йетса обеспечивает высокую случайность перестановок. Это важно для многих приложений, таких как случайные тесты, шифрование и симуляции.
4. Независимость от входных данных: Алгоритм Фишера — Йетса может быть применен к любому набору данных без необходимости знания их структуры или свойств. Это делает его универсальным инструментом для многих задач.
5. Псевдослучайность: Алгоритм Фишера — Йетса генерирует псевдослучайные перестановки, которые могут быть использованы во многих приложениях, где требуется случайность, но не обязательно истинная случайность.
В целом, алгоритм Фишера — Йетса интересен своей простотой, эффективностью и универсальностью. Он является полезным инструментом для многих задач, связанных с случайностью и перестановками данных.
//—————————————————————————————————————————————————————————————————————————————— void Shuffle (int & arr [], int size) { int index, temp; for (int i = size - 1; i > 0; i--) { index = MathRand () % (i + 1); temp = arr [i]; arr [i] = arr [index]; arr [index] = temp; } } //——————————————————————————————————————————————————————————————————————————————
3. Результаты тестов
Распечатка работы тасующего алгоритма прыгающих лягушек на тестовом стенде:
C_AO_SFL:50;25;15;5;0.7
=============================
5 Rastrigin's; Func runs 10000 result: 66.52578871476199
Score: 0.82429
25 Rastrigin's; Func runs 10000 result: 52.38937199890908
Score: 0.64913
500 Rastrigin's; Func runs 10000 result: 44.5591163558836
Score: 0.55211
=============================
5 Forest's; Func runs 10000 result: 0.5762718670482314
Score: 0.32597
25 Forest's; Func runs 10000 result: 0.16329693292687839
Score: 0.09237
500 Forest's; Func runs 10000 result: 0.04968320483668511
Score: 0.02810
=============================
5 Megacity's; Func runs 10000 result: 3.1599999999999997
Score: 0.26333
25 Megacity's; Func runs 10000 result: 1.016
Score: 0.08467
500 Megacity's; Func runs 10000 result: 0.3004
Score: 0.02503
=============================
All score: 2.84501
При наблюдении за анимацией работы алгоритма SFL не обнаруживается никакой кластеризации или группирования по отдельным мемам, хотя ожидалось обратное. Агенты (точки) оптимизации распределены по полю хаотично, и нет никаких закономерностей в движении частиц. Сразу заметно низкое качество сходимости алгоритма, что, к сожалению, проявляется в застревании в локальных экстремумах, что можно определить по долгим плавным участкам на графике сходимости. Однако с увеличением количества оптимизируемых параметров "ступенчатость" снижается.
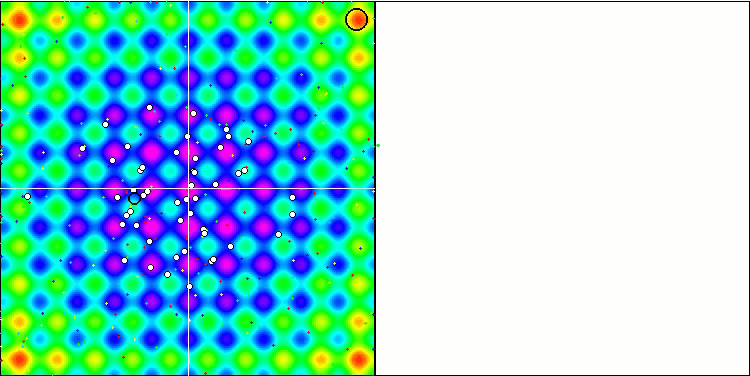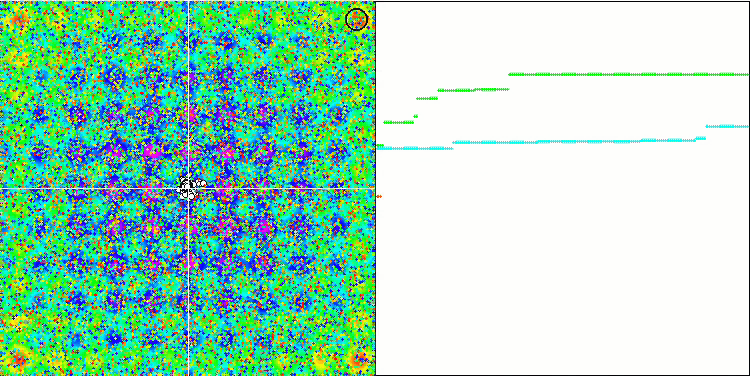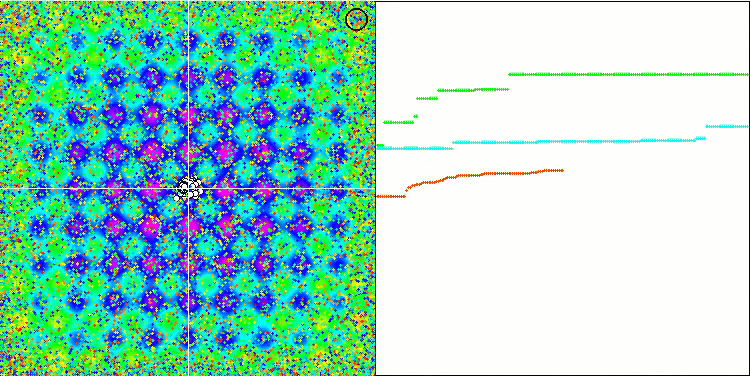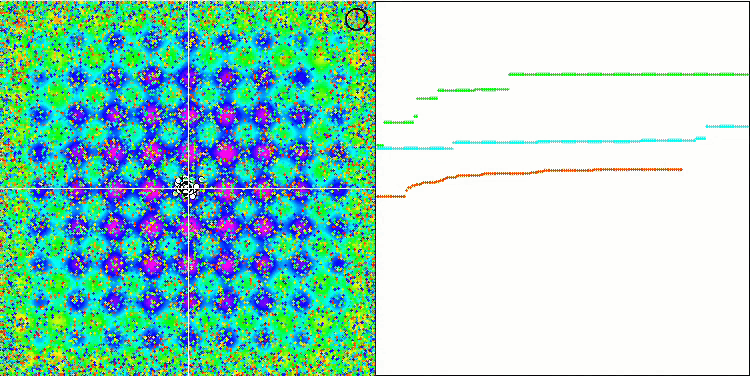
SFL на тестовой функции Rastrigin.
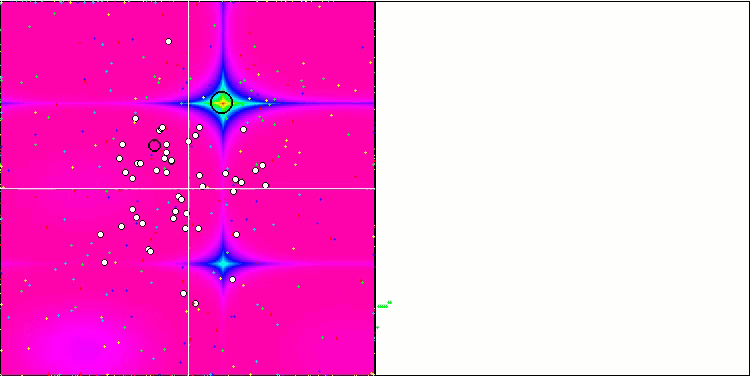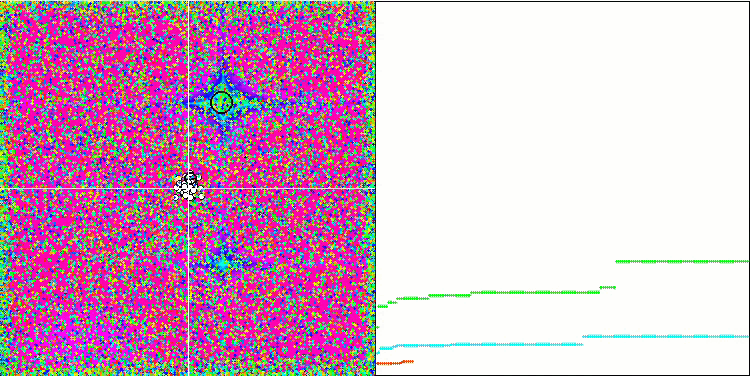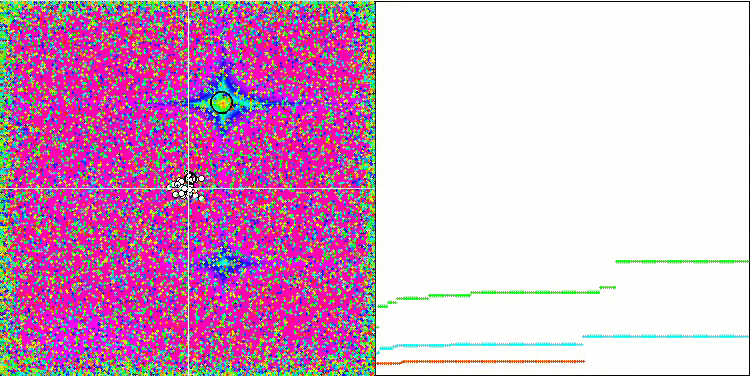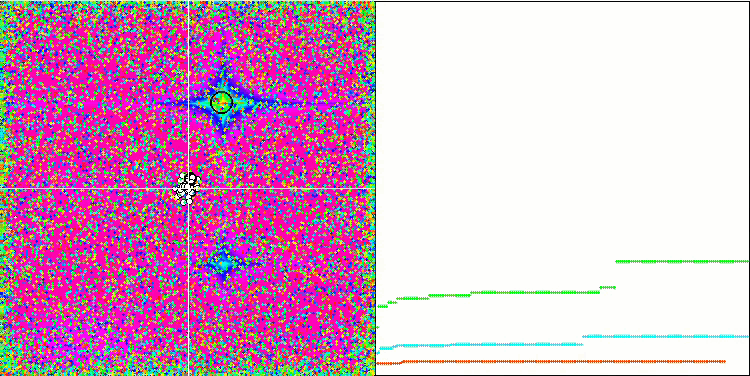
SFL на тестовой функции Forest.
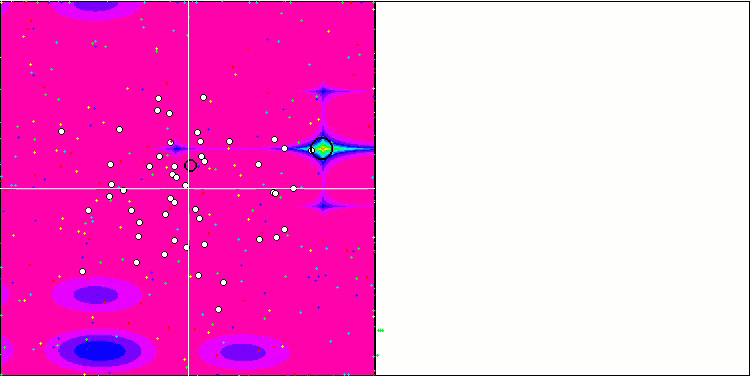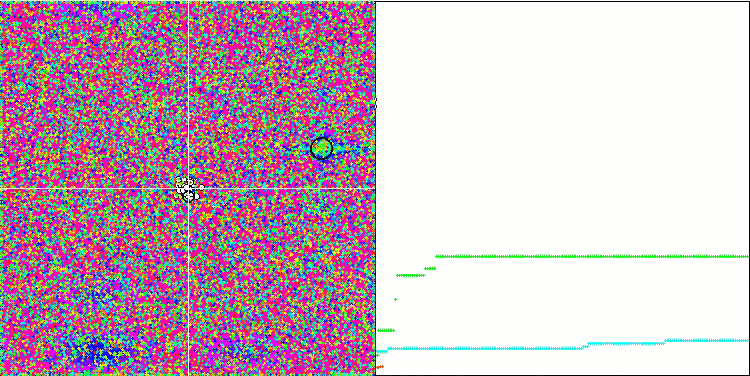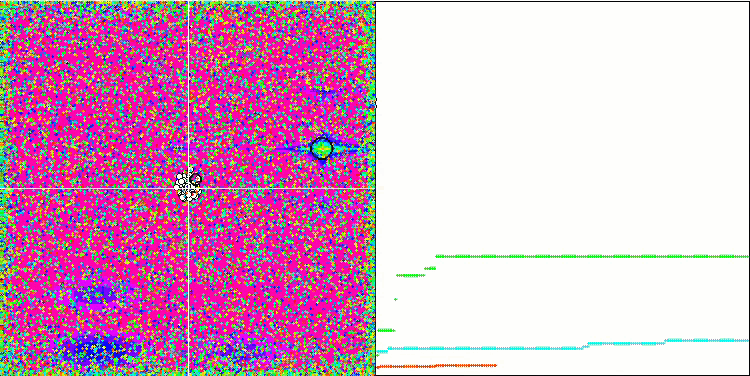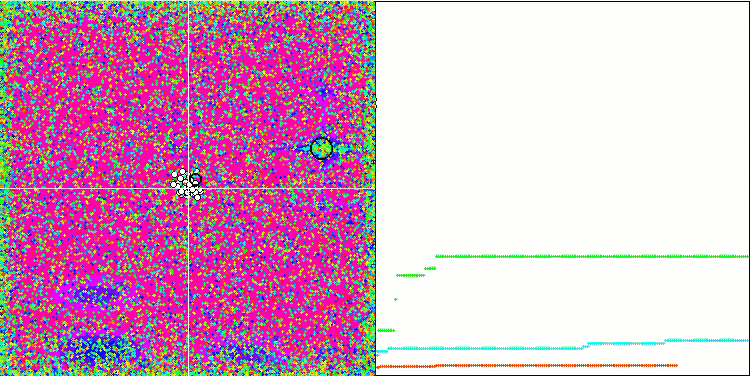
SFL на тестовой функции Megacity.
Перейдем к подведению итогов. При анализе таблицы с результатами тестирования алгоритмов можно заметить, что алгоритм SFL показывает ниже средних результатов в качестве оптимизации. Хотя на гладкой функции Растригина SFL имеет некоторое преимущество, оно недостаточно, чтобы рекомендовать его как предпочтительный алгоритм для гладких функций. На функциях с изломами Forest и Megacity тасующий алгоритм прыгающих лягушек демонстрирует худшие результаты по сравнению с гладкими функциями. Это можно объяснить тем, что на пологих участках оптимизируемой функции прыжки лягушек не улучшают их позицию, и они постоянно возвращаются на исходное место, не имея возможности "зацепиться" за рельеф.
| AO | Description | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | ||||||
| 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | ||||||
| SSG | saplings sowing and growing | 1,00000 | 1,00000 | 0,55665 | 2,55665 | 0,72740 | 0,94522 | 1,00000 | 2,67262 | 0,76364 | 0,85977 | 1,00000 | 2,62340 | 100,000 |
| HS | harmony search | 0,99676 | 0,95282 | 0,48178 | 2,43136 | 1,00000 | 0,98931 | 0,44806 | 2,43736 | 1,00000 | 1,00000 | 0,41537 | 2,41537 | 92,329 |
| ACOm | ant colony optimization M | 0,34611 | 0,17985 | 0,17044 | 0,69640 | 0,86888 | 1,00000 | 0,77362 | 2,64249 | 1,00000 | 0,88930 | 0,05606 | 1,94536 | 65,347 |
| IWO | invasive weed optimization | 0,95828 | 0,67083 | 0,29807 | 1,92719 | 0,70773 | 0,46349 | 0,31773 | 1,48896 | 0,80000 | 0,42067 | 0,33289 | 1,55356 | 61,104 |
| COAm | cuckoo optimization algorithm M | 0,92400 | 0,46794 | 0,26004 | 1,65199 | 0,58378 | 0,34034 | 0,16526 | 1,08939 | 0,72727 | 0,33025 | 0,17083 | 1,22835 | 47,612 |
| FAm | firefly algorithm M | 0,59825 | 0,33980 | 0,17135 | 1,10941 | 0,51073 | 0,42299 | 0,49790 | 1,43161 | 0,34545 | 0,28044 | 0,35258 | 0,97847 | 41,537 |
| ABC | artificial bee colony | 0,78170 | 0,32715 | 0,20822 | 1,31707 | 0,53837 | 0,21455 | 0,13344 | 0,88636 | 0,56364 | 0,26569 | 0,13926 | 0,96858 | 36,849 |
| GSA | gravitational search algorithm | 0,70167 | 0,45217 | 0,00000 | 1,15384 | 0,31660 | 0,36416 | 0,33204 | 1,01280 | 0,59395 | 0,35054 | 0,00000 | 0,94448 | 36,028 |
| BA | bat algorithm | 0,40526 | 0,63761 | 0,84451 | 1,88738 | 0,20841 | 0,17477 | 0,25989 | 0,64308 | 0,29698 | 0,09963 | 0,17371 | 0,57032 | 35,888 |
| BFO | bacterial foraging optimization | 0,67203 | 0,30963 | 0,11813 | 1,09979 | 0,39702 | 0,26623 | 0,20652 | 0,86976 | 0,52122 | 0,33211 | 0,18932 | 1,04264 | 34,693 |
| EM | electroMagnetism-like algorithm | 0,12235 | 0,46278 | 1,00000 | 1,58513 | 0,00000 | 0,03498 | 0,34880 | 0,38377 | 0,00000 | 0,00000 | 0,10924 | 0,10924 | 22,091 |
| SFL | shuffled frog-leaping | 0,40072 | 0,23739 | 0,26548 | 0,90360 | 0,20153 | 0,04147 | 0,02652 | 0,26952 | 0,27273 | 0,05535 | 0,06639 | 0,39446 | 15,203 |
| MA | monkey algorithm | 0,33192 | 0,33451 | 0,14644 | 0,81287 | 0,10012 | 0,07891 | 0,08932 | 0,26836 | 0,21818 | 0,04243 | 0,10720 | 0,36781 | 13,603 |
| FSS | fish school search | 0,46812 | 0,25337 | 0,11302 | 0,83451 | 0,12840 | 0,05013 | 0,06516 | 0,24369 | 0,16971 | 0,04796 | 0,08283 | 0,30050 | 12,655 |
| PSO | particle swarm optimisation | 0,20449 | 0,08200 | 0,07160 | 0,35809 | 0,18895 | 0,10486 | 0,21738 | 0,51119 | 0,23636 | 0,05903 | 0,01957 | 0,31496 | 10,031 |
| RND | random | 0,16826 | 0,09743 | 0,08019 | 0,34589 | 0,13496 | 0,04810 | 0,04715 | 0,23021 | 0,16971 | 0,03875 | 0,04922 | 0,25767 | 5,302 |
| GWO | grey wolf optimizer | 0,00000 | 0,00000 | 0,02256 | 0,02256 | 0,06570 | 0,00000 | 0,00000 | 0,06570 | 0,32727 | 0,07378 | 0,02557 | 0,42663 | 1,000 |
Выводы
SFL представляет собой скорее "надстройку" для других алгоритмов оптимизации, которые можно использовать как логику перемещения агентов в мемплексах, SFL и был изначально изобретён как методика улучшения качества оптимизации уже существующих алгоритмов. Как самостоятельный алгоритм оптимизации SFL демонстрирует результаты ниже средних среди популяционных алгоритмов, рассмотренных ранее. SFL имеет большие возможности экспериментирования с комбинированием логических шагов в алгоритме, повышающих как разведку, так и эксплуатацию. SFL обладает высокой гибкостью и адаптивностью, что делает его подходящим для специального использования в специфических задачах оптимизации.
Гистограмма результатов тестирования алгоритмов на рисунке 3 (по шкале от 0 до 100, чем больше тем лучше, в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье).
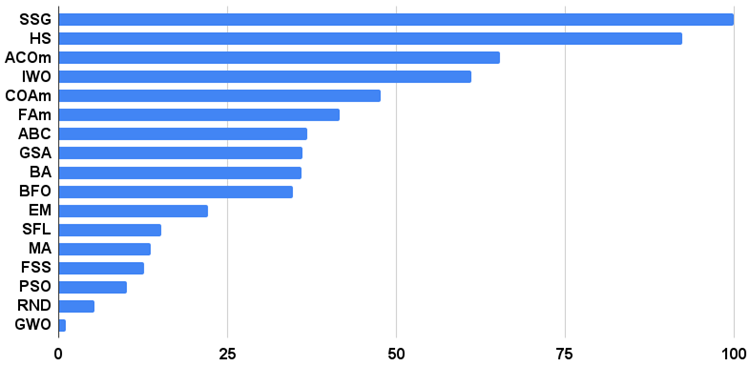
Рисунок 3. Гистограмма итоговых результатов тестирования алгоритмов.
Плюсы и минусы тасующего алгоритма прыгающих лягушек (SFL):
1. Небольшое количество внешних параметров.
2. Оригинальность архитектуры алгоритма, возможность использовать в мемах другие алгоритмы оптимизации.
Минусы:
1. Высокая вычислительная трудоёмкость.
2. Невысокие результаты на гладких и дискретных функциях.
3. Застревание на функциях с ровными горизонтальными "площадками".
К каждой статье я прикрепляю архив, содержащий обновленные актуальные версии кодов алгоритмов, описанных в предыдущих статьях. Статьи созданы на основе накопленного опыта автора и его личного мнения, выводы и суждения основываются на результатах проведенных экспериментов.
- Бесплатные приложения для трейдинга
- Форексный VPS бесплатно на 24 часа
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Набросал его просто потому, что если уж ваять какие-то навороты, то без потенциальных проблем - "зацепило" использование цикла с перебором строк (!) - может быть супер неэффективно в программах побольше.
В ini-файле не только строковые параметры, но и других типов (хотя представлены текстом).
Синглтон у фабрики - это нормально. Синглтон у объекта функции - в данном случае просто для работоспособности примера - можно реализовать множественность.
Использую string-решение на этапе инициализации. Думаю, меньше миллисекунды занимает. Честно говоря, не прочувствовал потенциальных проблем.
Спасибо автору за проделанную огромную работу и безвозмездную возможность использовать ее!
Немного смотрю код. И вот эту красоту заменил у себя на такой ужас.
А в чем выигрыш? Это же действительно ужас. Извините, если что))
По-хорошему, создание функции по запросу должно в самом классе сидеть (без плясок со строками и "завязкой" на совпадение фрагментов имен классов и элементов перечисления). Там есть вариант автора. Вот еще один - что-то вроде такого:
Файл Functions.mqh:
Использовать в скрипте так:
Извините, но я конечно же ошибаюсь, вот в той строке кода:
static FunctionInstance *pointers[] = {C_Function::fabric<C_Skin>(), C_Function::fabric<C_Forest>(), C_Function::fabric<C_Megacity>(), C_Function::fabric<C_Rastrigin>(), C_Function::fabric<C_Universe>()};не будут создаваться по объекту каждого типа?
...тогда как, за все время работы программы будет использоваться только один тип.
А в чем выигрыш? Это же действительно ужас. Извините, если что))
Сложный вопрос. Не знаю.
Извините, но я конечно же ошибаюсь, вот в той строке кода:
не будут создаваться по объекту каждого типа?
...тогда как, за все время работы программы будет использоваться только один тип.
В этой строчке создаются фабрики. Они действительно для всех классов резервируются (во время старта). Рабочий объект фабрика создает при явном вызове create.