
Model aramada brute force yaklaşımı (Bölüm II): Yoğunlaşma
Giriş
Bir önceki makalede başladığımız konuya devam etmeye karar verdim. Bu kez, değiştirilmiş uygulama sürümünü kullanarak döviz çiftlerinin derinlemesine bir analizini yapacağız. Kullanıcı Aleksey Vyazmikin'e projenin geliştirilmesine yaptığı katkılardan dolayı teşekkür ederim. Tavsiyeleri teknik açıdan çok yardım sağladı ve fikrin daha da gelişmesinde itici güç oldu. Bu çalışmaya bir sonraki makalede de devam edeceğim ve daha ilginç veriler ve sonuçlar sunacağım. Belirli bir döviz çiftinin analizinin etkinliğini global ölçekte göstermenin yanı sıra maksimum ve minimum süreli zaman aralıklarının analizindeki farkı göstermenin çok önemli olduğuna inanıyorum. Zamanım ve hesaplama kaynaklarım sınırlı olduğu için, yalnızca birkaç döviz çiftini yalnızca bir zaman dilimiyle inceleyebildim. Ancak bu, global modellerle ilk tanışma için yeterli görünmektedir. Verileri analiz ederken, bir önceki makaledeki verileri de kullanacağım.
Bu konu neden bu kadar ilginç?
Çoğu zaman MetaTrader 4 ve MetaTrader 5 Uzman Danışman programcıları için tüm fikirler sayısız kod satırı, sayısız test, optimizasyon, ileri ve geri testler anlamına gelir. Çoğu durumda da istediğimizi elde edemeyiz. Bazı programcılar bu özel durumdan sıkılır. Araştırma ve arama süreci bir rutine dönüşür. Eğer yaptığınız iş manevi tatmin ve para getirmiyorsa, o zaman o işi bırakma olasılığınız çok yüksektir. Bana da böyle oldu. Rutine veda etmeye ve bir makine tarafından başarıyla gerçekleştirilebilecek eylemleri otomatikleştirmeye karar verdim. Makinenin duyguları yoktur ve benim aksime ideal bir işçidir. Elbette makine bir insan kadar geniş bir düşünce yapısına sahip değildir, ancak çok fazla hesaplama kaynağına sahiptir ve bazı işlemleri daha kolay ve daha hızlı uygulayabilir. Evrim geçirebilen kendi sinir ağı mimarimi yazmaya başlamak ya da sorunu çözmek için en basit yaklaşımla başlamak olmak üzere iki seçeneğim vardı. Ben ikinci yaklaşımı kullanmaya karar verdim. Basitliğine rağmen proje, MQL ürünlerinin basit programlamasının aksine yaratıcılığa ve ilgiye yer veriyor. Evrensel bir şablon üzerinde çalışmak ve gerekli işlevselliği kademeli olarak ekleyerek daha da geliştirmek iyi bir fikirdir. Basit bir şablonla başlayabilir ve ardından belirli bir çalışma prensibi için yeni şablonlar oluşturabiliriz. Böylece sıkıcı rutinden kurtulabilir ve geliştirme sürecimize devam edebiliriz. Tembellik ilerlemenin babasıdır.
Brute force programının yeni sürümü ve değişikliklerin listesi
Programda kırmızı çerçeve içerisinde gösterilen tek bir değişiklik yapılmıştır. Bu ayar, en iyi performansını gösterdiği ikinci sekmeden alınmıştır. Bu ayarın eklenmesinin nedeni, nihai sonuçların kalitesi üzerinde çok güçlü bir etkiye sahip olmasıdır. Mesele şu ki, ilk sekmede analiz yapılırken, tüm sonuçlar başlangıçta kaliteye göre sıralanıyordu. Kalite kriteri olarak kâr faktörü veya puan cinsinden beklenen getiri kullanılıyordu. Ancak program grafik şeklini değerlendirmemize izin vermiyordu. Şekil kriteri olarak doğrusallık faktörü (düz bir çizgiye benzerlik) filtresini kullandım, bu da bizi her bir seçeneği görsel olarak kontrol etme ihtiyacından kurtarmaktadır. Burada, daha düz ve yumuşak grafiklerin ikinci sekmede yüksek kaliteli bir varyant verme olasılığının daha yüksek olduğu sonucuna varabiliriz. Ayrıca bu tür grafikler, ikinci sekmedeki benzer bir filtre tarafından reddedilecek daha az sayıda varyanta sahiptir. Bu değeri hesaplamak için ikinci bir geçiş gereklidir. Bu filtre etkinse, brute force hızı yaklaşık 2 kat daha yavaş olur. Ancak bizim için önemli olan hız değil, elde edilen birincil sonuçların kalitesidir, çünkü onların kalitesi daha sonra yapılacak her şeyin performansını etkileyecektir.
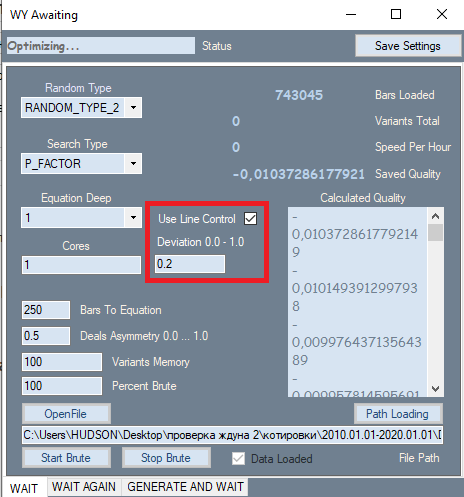
Eklenen filtreye ek olarak, polinomun kendisi de değiştirilmiştir. Artık polinom sadece belirli çubukların Close[i]-Open[i] değerlerini değil, aynı zamanda aşağıdaki değerleri de argüman olarak kabul etmektedir:
- Close[i]-Open[i]
- High[i]-Open[i]
- Low[i]-Close[i]
- Low[i]-Open[i]
- High[i]-Close[i]
Artık formül, programın önceki sürümünden farklı olarak belirli bir çubuğun tüm fiyat verilerini içermektedir. Bu da polinomun karmaşıklığını büyük ölçüde artırarak brute force hızının düşmesine neden olmaktadır. Ancak şimdi, yeterli hesaplama kaynağına sahip olmamız koşuluyla, daha iyi ve daha verimli piyasa formülleri seçebiliriz. Elbette bu verilerle başka değişkenler de yaratabiliriz. Ancak bu değerler polinomda kullanıldığında, örneğin yukarıdaki değerlerin doğrusal bir kombinasyonu olabilecek değerleri elde edersiniz:
- NewQuant = C1*(High[i]-Close[i])+C2*(Low[i]-Close[i])
- C1 = 1 ve C2 = -1 ise
- NewQuant = (High[i]-Close[i])-(Low[i]-Close[i]) = High[i]-Low[i]
- diğer durumlarda
- NewQuant = (C1-C3)*(High[i]-Close[i])+(C2+C3)*(Low[i]-Close[i])+C3*((High[i]-Close[i])-(Low[i]-Close[i])) = (C1-C3)*(High[i]-Close[i])+(C2-C3)*(Low[i]-Close[i])+C3*(High[i]-Low[i])
Başka bir deyişle, değişkenlerin doğrusal bir kombinasyonunu kullanarak, ki bunlar da diğer değişkenlerin doğrusal kombinasyonlarından oluşur, temel formüle dahil etmeden yeni değişkenler oluşturabiliriz. Formülde zaten mevcut olan diğer değişkenlerden oluşturulabilecek değişkenleri dahil etmemeye çalışmak daha iyidir. Onlar, katsayıların kendi değerlerine bağlı olarak katsayıların seçimi sırasında görünecektir.
Sonuç olarak, yeni polinom çok daha karmaşık olacaktır:
- Y = Sum(0,NC-1)(C[i]*Varyant(x[1]^p[1]*x[2]^p[2]...*x[N]^p[N]))
- MaxPowOfPolinom = Sum(0,N)(p[i])
- NC - seçilen katsayıların sayısına eşit olan polinomdaki toplam terim sayısı
Burada x[i] polinomun aldığı argümanlardır ve p[i] argümanın yükseltildiği derecedir. Tüm kurucu çarpanların toplam derecesi polinomumuz için izin verilen sayıyı aşmamalıdır, çünkü hiçbir bilgisayar bu tür karmaşık açılımları işleyemez. Formül için çubuk sayısı minimuma yakın olduğunda, neredeyse her zaman 1. dereceyi, nadir olarak da 2. veya 3. dereceyi kullanırım. Sunucularda bile daha yüksek derecelerin kullanılması etkisizdir. Yeterli hesaplama gücü yoktur.
Argüman seçenekleri aşağıdadır. Nihai toplam, tüm olası çarpım kombinasyonlarını içerir:
- x[i] = Close[i]-Open[i]
- x[i] = High[i]-Open[i]
- x[i] = Low[i]-Close[i]
- x[i] = High[i]-Open[i]
- x[i] = High[i]-Close[i]
Tüm bu işlemleri neden polinom ile gerçekleştirdiğimizi de açıklığa kavuşturmak isterim. Mesele şu ki, her sistem nihayetinde bir koşullar kümesine bağlıdır. Bir veya birden fazla koşul olabilir, bu önemli değildir, çünkü koşullar mantıksal bir fonksiyondur. Koşullar kümesi, sonuçta true veya false geri döndüren bir boolean ifadesine dönüştürülebilir. Böyle bir sinyal sadece Evet veya Hayır olarak yorumlanabilir. Ancak sinyalin ne kadar güçlü olduğunu belirlemek veya onu ayarlamak mümkün değildir. Sinyal olarak birkaç gösterge kullanırsanız, bu göstergelerin parametrelerini ayrı ayrı ayarlayabilirsiniz; bu, nihai mantıksal ifadede bir değişikliğe veya sinyalde bir değişikliğe yol açacak ve bu da sonuçta ticareti etkileyecektir. Ancak bunun son derece sakıncalı olduğunu düşünüyorum, çünkü belirli bir göstergenin bir veya başka bir parametresini değiştirerek, bunun ticareti nasıl etkileyeceğini bilemeyeceğiz.
Bu yaklaşımın arkasındaki ana fikir basitlik ve verimliliktir. Neden tam olarak bu yaklaşım? Çeşitli avantajları vardır:
- Optimize edilen fonksiyonun tekilliği
- Sinyal gücünün fonksiyon değerine bağımlılığı
- Kullanım kolaylığı
- Optimize edilebilir tek parametre polinom değeridir
En önemli şey, koşulların sayısını ve türünü seçmemize gerek olmamasıdır. Bunun nedeni, başlangıçta sonsuz bir koşullar kümesi aramak yerine, tüm bu koşulları pozitif kesirli veya negatif kesirli bir sayı veren tek bir fonksiyona indirgeyebileceğimiz fikrini kabul etmemizdir. Bir veya başka bir fonksiyonun güvenilirliğine bağlı olarak, modülde daha güçlü bir sinyal gerektirebilir. Bazı formüllerde bu ölçeklenebilirlik sağlayabilir. Burada ölçeklenebilirlik, işlem sayısı azalırken sinyali güçlendirme yeteneği anlamına gelir.
Genel olarak konuşmak gerekirse, benim ve diğer pek çok kişinin araştırması tek bir sonuca varıyor. Giriş sinyalini güçlendirmeye yönelik bir girişim, kaçınılmaz olarak sabit bir süre içerisinde işlem sayısının azalmasına yol açmaktadır. Başka bir deyişle, rastgele bir bileşene sahip herhangi bir fonksiyon için, bazı noktalar her zaman diğer noktalardan daha öngörülebilir bir sonuca sahiptir. Fonksiyonumuz yeterince verimliyse, bu fonksiyon tarafından sağlanan sinyal için artan gereksinimlerle belirli bir öngörülebilirlik seviyesine ulaşabilir. Elbette bu, birincil gereksinimlerimizi karşılayan her fonksiyon için geçerli değildir. Ancak birincil gereksinimler ne kadar katı olursa, brute force yaklaşımını kullanarak bulabileceğimiz formül varyantlarının beklenen getirisi de o kadar yüksek olur. Bu, gradyan artırmanın yanı sıra sinir ağları da dahil olmak üzere diğer model arama yöntemleri için de geçerlidir.
Çoğu veri örneklemine bağlıdır. Örneklem ne kadar küçük olursa, rastgele bir sonuç elde etme olasılığı da o kadar artar. Burada rastgele bir sonuç, modelin arandığı sembolün global geçmişi üzerinde nihai sistemi test ederken ya çalışmayan ya da son derece etkisiz çalışan bir sonuçtur.
Nihai ticaret sisteminin gelecekteki kalitesinin analiz edilen veri alanının büyüklüğüne ve bu sistemi bulmak için gereken emek miktarına nasıl bağlı olduğu sorusuna cevap vermeye çalışacağız. İlk olarak, sabit bir süre boyunca bulunan stratejilerin sayısının matematiksel beklentisinin formülünü tanımlayalım:
- Mn(t) = W(t,F)*Ef(T,N,L)
- Mn - gereksinimlerimizi karşılayan bulunan stratejilerin sayısına ilişkin matematiksel beklenti
- W(t,F) = F*t - birim zaman başına kontrol edilen varyant sayısı
- Ef(T,N,L) = ? - aralık uzunluğuna, fiyat türüne, gerekli kapalı emir sayısına ve brute force sırasında dikkate alınırsa gerekli doğrusallık faktörüne bağlı olan brute force verimliliği (bu değer, mevcut varyantın sonuçlarının gerekli ve yeterli değerleri alma olasılığına eşittir)
- N - testimiz için yeterli olacak izin verilen minimum işlem sayısı
- L - izin verilen maksimum doğrusallık faktörü (ek bir kontrol kriteri olarak)
- F - strateji varyantları brute force frekansı
Ef fonksiyonunun biçimini belirlemek son derece zordur, ancak nasıl görüneceğini ve hangi özelliklere sahip olduğunu kabaca tahmin edebiliriz:
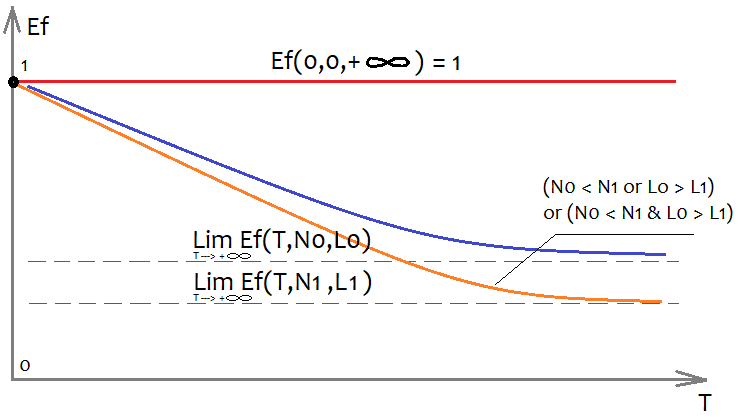
Çok boyutlu bir fonksiyonu düzlem üzerinde gösterebilmek için, grafiğin kendisinin oluşturulduğu bir argüman hariç, tüm argümanlarını bazı sayılarla sabitlemek gerekir. Tek bir zaman dilimini analiz etmemiz şartıyla, analiz edilen örneklemin zaman içerisindeki süresini ifade eden T değişkeni özellikle ilginçtir. Bu varsayımı bir kenara bırakırsak, örneklem büyüklüğünü T olarak alabiliriz - bu grafik görünümünü değiştirmeyecektir. Doğal olarak, kalan 2 argümanın grafik görünümünü nasıl etkileyeceği ile ilgileniyoruz. Bu durum şekilde gösterilmektedir. Son halinde ne kadar çok emir olmasını istiyorsak, gereksinimlerimizi karşılayan o kadar az sistem bulacağız, çünkü daha az emre sahip bir sistem bulmak çok daha kolaydır. Aynı husus doğrusallık faktörü (düz bir çizgiden sapma) için de geçerlidir, ancak burada daha iyi doğrusallık faktörü daha küçük olanıdır (sıfıra eğilimlidir).
Sistem kalitesi kavramını sabitlemezsek (çünkü bu değer hem bir kâr faktörü hem de bir matematiksel beklenti olabilir), o zaman bulunan sistemin maksimum kalitesi kavramını da tanıtabiliriz. Neye bağlı olduğunu da benzer şekilde tanımlayabiliriz:
- Mq = Mq(T,N,S)
- S - seçilen formül yapılandırması
Diğer bir deyişle, stratejinin mümkün olan en yüksek kalitesi doğrudan formülümüzün etkinliğinin yanı sıra gereksinimlerimize ve aralığın karmaşıklığına bağlıdır. Aynı zamanda, hala alanın başlangıcının sabit olduğunu ve eğitim başlangıç noktasının her varyasyonunun benzersiz olduğunu ve benzersiz başlangıç parametreleri verdiğini varsayıyoruz. Başka bir deyişle, eğitim alanı için farklı bir başlangıç tarihi seçerek, farklı verimlilik değeri ve diğer parametrelerin yanı sıra elde edilen sistemlerin nihai kalitesini de elde edeceğiz.
Her bir kalite türünün maksimum değeri olduğu anlayışına da varabiliriz, örneğin kâr faktörünün maksimum kalitesi sonsuzdur, ancak bu ölçüyü analiz için kullanmayı sevmiyorum, çünkü maksimum değeri sınırlı değildir ve dolayısıyla PF ile grafiksel modellerin anlaşılması daha zor olacaktır. Bu nedenle, kendi PF analoğum olan P_FACTOR'ı kullanıyorum. [-1,1] aralığında yer alır.
- P_FACTOR = (Profit-Loss)/(Profit+Loss)
Maksimum değeri 1'e eşittir ve böylece çalışmak için daha uygundur. İşte T'ye (seçilen alan ve örneklem) bağlı olarak bu değerin maksimumunu tanımlayan fonksiyon:
- Mx = Mx(T)
Parametre veya kalite kriteri P_FACTOR ise, Mx(T) = 1 olur. Fonksiyon biçimi bilinmeyebilir, ancak T ekseninin tüm pozitif kısmı boyunca Mx'(T) > 0 olduğu bilinmektedir. Bu, değerin herhangi bir noktada pozitif olduğu ve dolayısıyla grafiğin her zaman arttığı anlamına gelir.
Kâr faktörü açısından şu şekilde görünecektir:
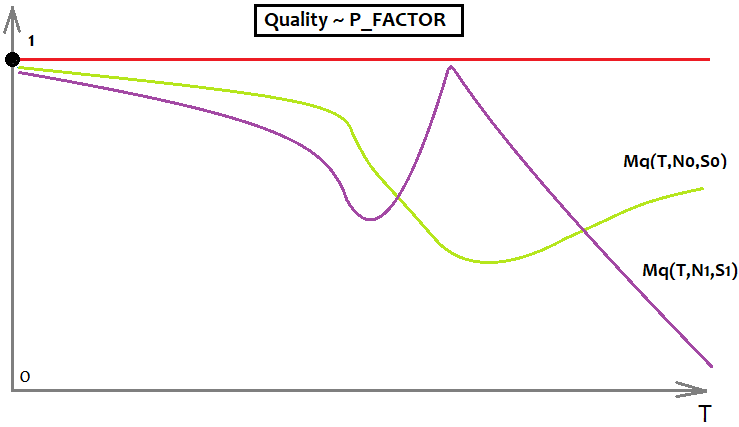
Bu örnekte PF'nin bir üst sınırı ve farklı gereksinimleri olan iki farklı formülü gösteren iki grafik bulunmaktadır. Grafikte, limon rengi olan formül daha iyidir, çünkü "T" sonsuza giderken kalite solmasına daha az eğilimlidir.
Bu, matematiksel beklenti için aşağıdaki gibi görünecektir:
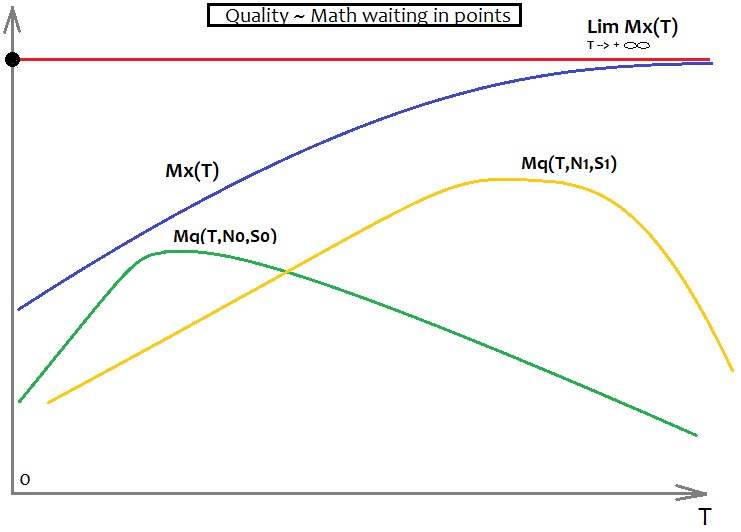
Burada yine farklı gereksinimleri olan iki farklı formül için iki varyantımız vardır. Ayrıca burada asimptot görevi gören Mx(T) bulunmaktadır - Mq(T,N,S) bu engeli aşamaz. İdeal Mq(T,N,S), Mx(T) grafiğiyle eşleşecektir ve kutsal kaseyi bulduğumuz anlamına gelecektir. Tabii ki bu gerçekte asla gerçekleşmeyecektir. Ancak, piyasayı gerçekten anlamak istiyorsanız, bunun piyasanın doğru anlaşılması için çok önemli olduğuna inanıyorum.
Forex'te de diğer finans piyasalarında olduğu gibi sadece olasılık teorisi kavramları ile ticaret yapmak en doğru ve isabetlisidir. İşte forex piyasası için ana matematiksel analiz kurallarından bazıları:
- Neredeyse tüm büyüklükler sabit değildir ve matematiksel beklentileriyle değiştirilir
- Daha büyük bir örneklemden elde edilen değerlerin matematiksel beklentileri, global bir örneklemden elde edilen sonuca eğilimlidir
- Olasılıkları daha sık kullanın
Veri segmentinin güvenilirliği sadece bir örneklem ölçüsüdür. Örneklem ne kadar büyük, girdi veri kümesi ne kadar kapsamlı olursa, nihai formül de o kadar adil olur. Gerçek şu ki, örnek sonsuza doğru ilerledikçe, nihai sonuç sabit bir sınır değerine yönelecektir.
Şablon değişiklikleri
Mantık geliştirildiğinden, düzgün çalışmasını sağlamak için şablondaki fonksiyonları da değiştirmemiz gerekir. Yeni parametreleri kabul edebilmeleri gerekir. Bu fonksiyonların uygulanması hem programda hem de şablon kodunda aynıdır. Orijinal fonksiyonlar tek bir değerle çalışmak üzere geliştirilmişti, ancak şimdi 4 tane daha değerimiz vardır, bu yüzden fonksiyonları revize etmemiz gerekiyor. Her şeyden önce, bu değişiklikler daha yüksek kalitede formüller sağlamalıdır. Bir formülde ne kadar çok veri kullanılırsa, arama yetenekleri de o kadar yüksek olur.
Bu makaleyi yazarken, kodumda çarpanların kombinasyonlarının tekrarlanabileceği gerçeğiyle ilgili bir kusur buldum: çok boyutlu bir polinomu uygulayan fonksiyonun özellikleri nedeniyle bu çarpanların sırası kaotiktir. Bu fonksiyon bir çağrı ağacı oluşturur, ancak öğelerin permütasyonlarını kontrol edemez. Bu durum iki şekilde önlenebilir:
- Çarpanların tüm olası permütasyonlarını kontrol edebiliriz
- Formüldeki yinelenen çarpanların sayısını, toplam katsayıyı onların sayısına bölerek telafi edebiliriz
Ben ikinci seçeneği kullanmaya karar verdim. Bu yaklaşımın dezavantajı, ortalama katsayının 0.5'e doğru eğilim göstermesidir. En azından çarpanlar işe yaramaz olmayacaktır. Bu makale için hatadan etkilenmeyen 1. dereceden bir polinom kullandım. Sabit bir toplam dereceye sahip bir çarpan için kombinasyon sayısını kolayca hesaplayabiliriz:
- Comb = n!/(n-k)!
- n - olası bağımsız çarpanların sayısı
- k - son terimin toplam derecesi
Aşağıda bu formülün koddaki uygulaması yer almaktadır:
double Combinations(int k,int n) { int i1=1; int i2=1; for ( int i=n; i<n-k; i-- ) i1*=i; for ( int i=n-k; i>1; i-- ) i2*=i; return double(i1/i2); }
İşte nihai polinomun ana fonksiyonunun nasıl değiştiği. Değişiklikler tek boyutlu polinom kısmıyla ilgilidir, çünkü artık 1 çubuk parametresine değil, 5 tanesine bağlıyız. Tabii ki, 4 başlangıç dizisi vardır. Ancak fiyat verileri sadece veri olarak kullanılamaz, bazı daha esnek değerlere dönüştürülmeleri gerekir. Komşu fiyatlar arasındaki farkı kullanıyoruz, komşu fiyatlar ise hem çubuk açılışları hem de kapanışları olabilir.
double Val; int iterator; double PolinomTrade()//Polynomial for trading { Val=0; iterator=0; if ( DeepBruteX <= 1 ) { for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*(Close[i+1]-Open[i+1])/Point; iterator++; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*(High[i+1]-Open[i+1])/Point; iterator++; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*(Open[i+1]-Low[i+1])/Point; iterator++; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*(High[i+1]-Close[i+1])/Point; iterator++; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*(Close[i+1]-Low[i+1])/Point; iterator++; } return Val; } else { CalcDeep(C1,CNum,DeepBruteX); return ValStart; } } ///Fractal calculation of numbers double ValW;//the number where everything is multiplied (and then added to ValStart) uint NumC;//the current number for the coefficient double ValStart;//the number where to add everything void Deep(double &Ci0[],int Nums,int deepC,int deepStart,double Val0=1.0)//intermediary fractal { for ( int i=0; i<Nums; i++ ) { if (deepC > 1) { ValW=(Close[i+1]-Open[i+1])*Val0; Deep(Ci0,Nums,deepC-1,deepStart,ValW); } else { ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Open[i+1])*Val0/Point; NumC++; } } for ( int i=0; i<Nums; i++ ) { if (deepC > 1) { ValW=(High[i+1]-Open[i+1])*Val0; Deep(Ci0,Nums,deepC-1,deepStart,ValW); } else { ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Open[i+1])*Val0/Point; NumC++; } } for ( int i=0; i<Nums; i++ ) { if (deepC > 1) { ValW=(Open[i+1]-Low[i+1])*Val0; Deep(Ci0,Nums,deepC-1,deepStart,ValW); } else { ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Open[i+1]-Low[i+1])*Val0/Point; NumC++; } } for ( int i=0; i<Nums; i++ ) { if (deepC > 1) { ValW=(High[i+1]-Close[i+1])*Val0; Deep(Ci0,Nums,deepC-1,deepStart,ValW); } else { ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Close[i+1])*Val0/Point; NumC++; } } for ( int i=0; i<Nums; i++ ) { if (deepC > 1) { ValW=(Close[i+1]-Low[i+1])*Val0; Deep(Ci0,Nums,deepC-1,deepStart,ValW); } else { ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Low[i+1])*Val0/Point; NumC++; } } } void CalcDeep(double &Ci0[],int Nums,int deepC=1) { NumC=0; ValStart=0.0; for ( int i=0; i<deepC; i++ ) Deep(Ci0,Nums,i+1,i+1); }
Bazı küçük değişiklikler, katsayı dizisinin büyüklüğünü hesaplayan fonksiyonla ilgilidir. Şimdi döngü 5 kat daha uzundur:
int NumCAll=0;//size of the array of coefficients void DeepN(int Nums,int deepC=1)//intermediate fractal { for ( int i=0; i<Nums*5; i++ ) { if (deepC > 1) DeepN(Nums,deepC-1); else NumCAll++; } } void CalcDeepN(int Nums,int deepC=1) { NumCAll=0; for ( int i=0; i<deepC; i++ ) DeepN(Nums,i+1); }
Tüm bu fonksiyonlar nihai polinomu uygulamak için gereklidir. OOP burada gereksizdir ve özellikle açıkça yazılamayan formüller için (çok boyutlu açılımlar gibi) bir çağrı ağacı oluşturmak adına benzer fonksiyonları kullanmak daha iyidir. Mantıklarını anlamak oldukça zordur, ancak mümkündür. Bu fonksiyonların analogları C# programı içerisinde uygulanmaktadır. Ne yazık ki, ekteki Uzman Danışmanlar bu koda sahip değildir, ancak önceki sürümü kullanmaktadırlar. Oldukça beceriksiz olsa da oldukça etkilidir. Program henüz prototip aşamasında olup daha sonra geliştirilecek ve tamamlanacaktır. Şimdiye kadar, program sıradan bilgisayarlarda global modelleri analiz etmek için uygun değildir. Programımda hala pek çok küçük kusur vardır ve hataları tespit edip düzeltmeye devam ediyorum. Böylece programın yetenekleri sürekli büyüyerek istenen duruma yaklaşmaktadır.
Bulunan modelleri analiz etme
Bilgisayar kapasitem ve zamanım sınırlı olduğu için veri miktarını sınırlamak zorunda kaldım. Ancak yine de bazı sonuçlara varmak için yeterli olduğunu düşünüyorum. Özellikle, global modellerin analizi için yalnızca H1 grafiklerini kullanmam ve analiz süresini sınırlamam gerekiyordu. Tüm testler MetaTrader 4'te gerçekleştirilecektir. Mesele şu ki, bulunan modellerin matematiksel beklentisi makas seviyesine yakındır ve MetaTrader 5'te sınayıcı, özel test sembolü ayarları seçeneğini kullandığımızda bile tarihsel olarak kayıtlı değerden daha az olmayan bir makas uygular. Değer, mevcut brokerdan alınan gerçek tik verilerine ve seçilen alandaki makasa göre ayarlanır. Bu, çok iyimser test sonuçlarının üretilmesini önler. Bu mekanizmanın etkisini ortadan kaldırmak istedim ve MetaTrader 4 kullanmaya karar verdim.
Global modellerle başlayacağım. Matematiksel beklentileri 8 puan civarındaydı. Bunun nedeni, formül için 50 mum kullanmamız ve ilk sekmede, yalnızca 1 çekirdek kullanırken her döviz çifti için yaklaşık 200.000 varyantı kontrol etmemizdir. Daha iyi bir makineyle daha kolay olurdu. Programın bir sonraki sürümü bilgisayar gücüne daha az bağımlı olacaktır. Burada puan olarak ortaya çıkan matematik beklentisine değil, performansın gelecekteki Uzman Danışman performansını nasıl etkileyeceğine odaklanmak istiyorum.
EURUSD H1 ile başlayalım. Testler 2010.01.01-2020.01.01 aralığında gerçekleştirilmiştir. Amacı global bir model bulmaktı:
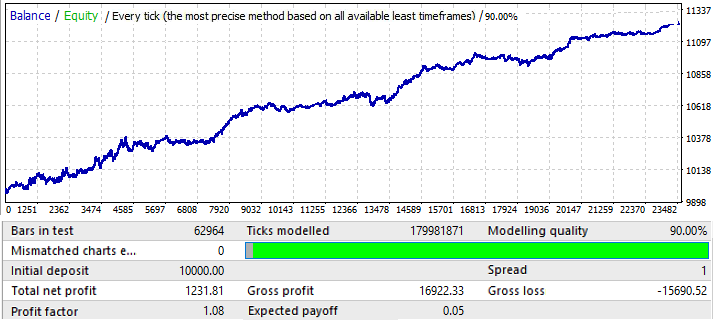
Sonuçlar göze pek hoş gelmiyor, ancak ilgili zaman aralığında döviz çiftinden elde edebildiğimiz tek şey budur. Çok net olmasa da global bir model tanımlayabiliriz. Brute force için formülde 50 mum kullandım. Sonuç beklediğimiz kadar iyi değildir, ancak gereklidir. Ne için olduğunu daha sonra göreceksiniz. Gelecekteki performansını anlamak için aynı segmenti 2020.01.01-2020.11.01 ileri döneminde test edelim:
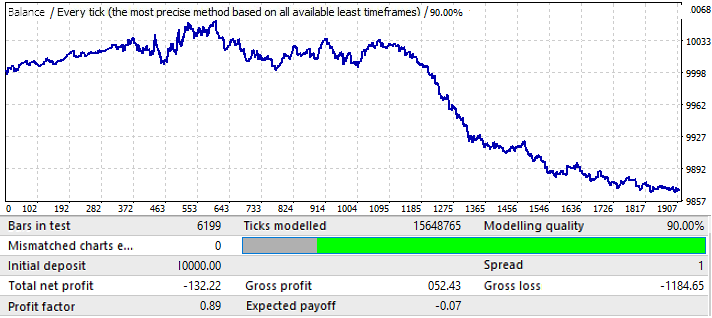
Sonuçlar oldukça anlaşılabilir. Bu analizin, modelin devamından kâr elde etmeye çalışmak için yetersiz olduğu ortaya çıktı. Genel olarak, global modelleri analiz ediyorsak, amaç en az birkaç yıl daha çalışacak bir model bulmak olmalıdır, aksi takdirde böyle bir analiz tamamen yararsızdır. Grafiğin başında model çalışmaya devam eder, ancak altı ay sonra tersine döner. Dolayısıyla, ilk test için yeterince iyi parametreler bulmayı başarmamız koşuluyla, böyle bir analiz birkaç ay boyunca ticaret yapmak için yeterli olabilir. Bu durumda analiz P_Factor değerine göre yapılmıştır. Bu parametre Kâr Faktörüne benzerdir, ancak [0...1] aralığında değerler alır. Kârın %1 ila %100 aralığıdır. İlk sekmede, bu parametrenin en yüksek değeri yaklaşık 0.029’du. Bulunan tüm varyantların ortalama değeri yaklaşık 0.02’ydi.
Bir sonraki EURCHF grafiği:
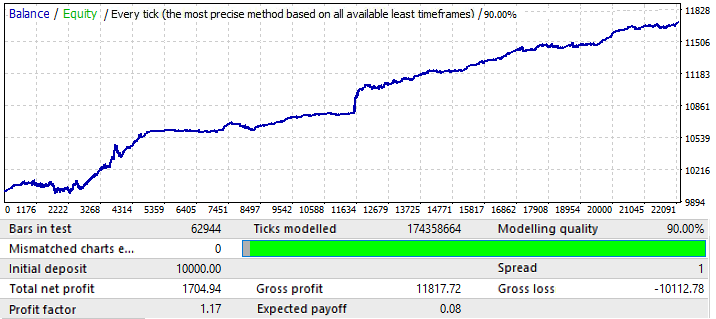
İlk sekmedeki grafik varyantları için maksimum sonuç 0.057 civarındaydı. Öngörülebilirlik derecesi bir önceki grafikten 2 kat daha yüksektir ve bu da bir öncekinden 0.09 daha yüksek olan nihai Kâr Faktörünü etkilemiştir. Bakalım global göstergelerdeki iyileşme ileri dönemi etkilemiş mi?
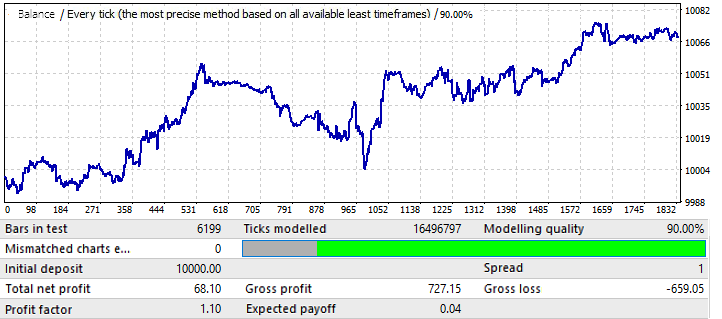
Gördüğünüz gibi, bu model yıl boyunca devam etmektedir. Çok eşit değildir ve kâr faktörü daha düşüktür. Bununla birlikte, bazı ön sonuçlar çıkarabiliriz. Aslında PF daha düşüktür çünkü global testte oldukça geniş alanlarda keskin bakiye büyümesi yaşanmış ve bu da ortaya çıkan kâr faktörünü artırmıştır. Eminim ki bunu önümüzdeki birkaç yıl için test edersek sonuç hemen hemen aynı olacaktır. Ön sonuç, grafik kalitesinde ve görünümünde yapılacak bir iyileştirmenin gelecekteki performansını etkileyeceği yönündedir. Dolayısıyla, ayarlarımızı bu belirli döviz çiftine uygulayarak bu sonucu elde ettik. Grafikteki dalgaların nedeni, bakiye dalgalanmalarının son yıllarda büyük ölçüde arttığı global testte görülebilir. Yani, dalgalar sadece bu dalgalanmaların bir devamıdır.
USDJPY grafiğine geçiyoruz:
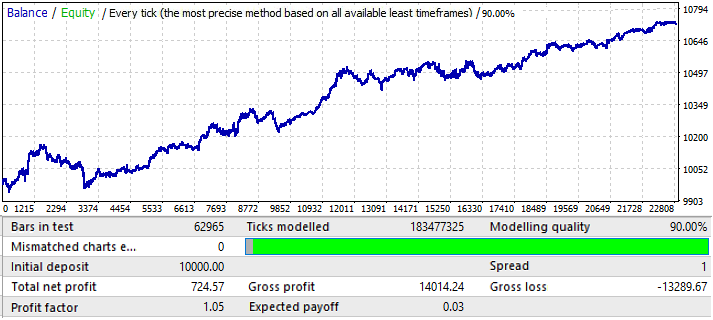
Bu en kötü grafiktir. İleri dönemi kontrol edelim:
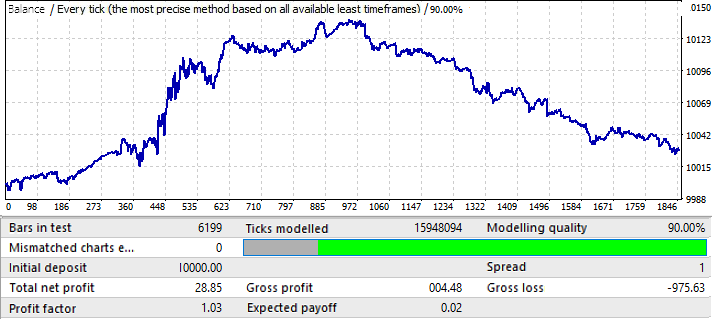
Pozitif bir bölgede görünmektedir, ancak ikinci yarısı, yukarı doğru bir hareketle başlayan, ardından tersine dönen ve neredeyse düz bir aşağı doğru harekete sahip olan ilk grafiğe (EURUSD H1) çok benzemektedir. Dolayısıyla, sonuçlar burada da aynıdır. Nihai sonuç kalitesi yeterince yüksek değildir. Yine de, matematiksel beklenti ve kâr faktörünün yeterince iyi olması koşuluyla, bu modelle birkaç ay kârlı ticaret bekleyebiliriz.
Son grafik, USDCHF’tir:
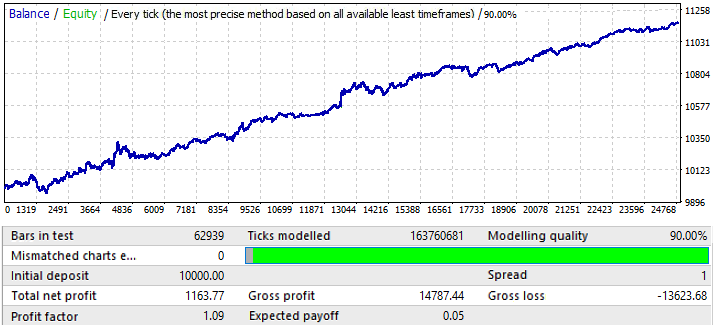
Çok etkileyici değildir. Önümüzdeki döneme bir göz atalım:
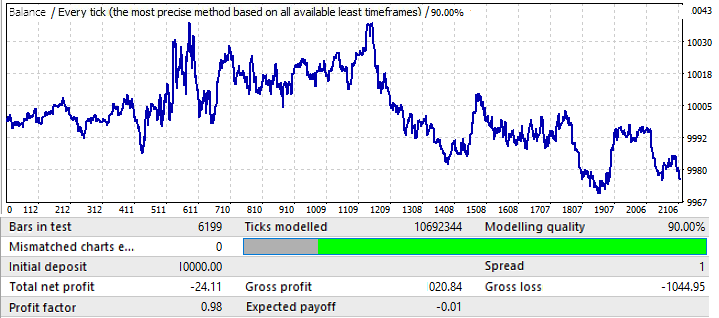
EURCHF hariç diğer grafiklere benzer görünmektedir. Yılın ortasına kadar performansı iyidir ve daha sonra bir tersine dönüş ve bir model tersine dönüşü vardır.
Aşağıdaki ön sonuçları çıkarabiliriz:
- Açıkçası EURCHF en iyi grafikti
- EURCHF, hem eğitim döneminde hem de ileri testte diğer tüm döviz çiftlerinden daha iyiydi
- EURCHF hariç tüm grafiklerde model yıl ortasına kadar korundu
Yukarıdakilere dayanarak, eğitim dönemindeki kalite sonuçlarının ileri dönem performansını doğrudan etkilediği sonucuna varabiliriz. Nihai sonucun kâr faktöründeki bir artış, sonucun diğer grafiklere göre çok daha az rastgele olduğunu yansıtabilir. Bu da global bir model bulduğumuzu gösterebilir. Forex piyasasına uygulandığı gibi, "herhangi bir modelde bir modelin payı vardır" diyebiliriz. Test değerleri ne kadar güçlü olursa bu pay da o kadar yüksek olur.
Şimdi örneklem büyüklüğünü değiştirmeye çalışacağım. 1 yıl kullanalım. 2017.01.01-2018.01.01 EURJPY H1. Gelecekte bir ay ileride modelin nasıl davranacağını görelim:
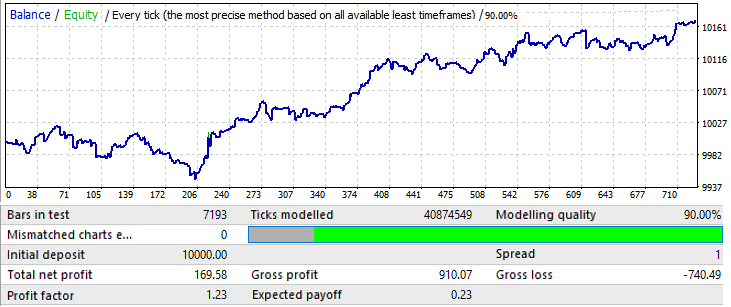
Grafik çok iyi görünmüyor, ancak ortaya çıkan kâr faktörü ve matematiksel beklenti 10 yıllık varyantlardan daha yüksektir. Örneklem ilk varyantlardan 12 kat daha küçüktür, ancak bu veriler göz ardı edilmemelidir.
İleri dönem 1 aydır: 2018.01.01-2018.02.01:
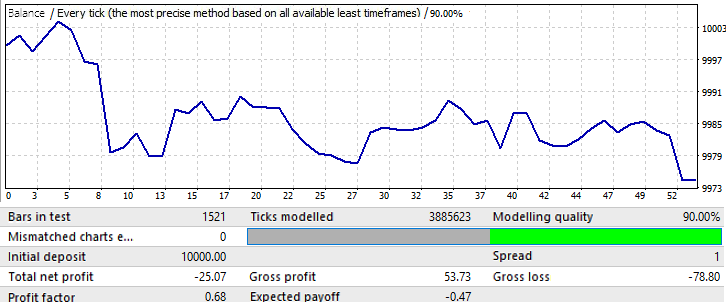
Bu sadece mantığı daha net hale getirmek için bir örnektir. Burada model neredeyse hemen tersine dönmektedir. Ne yazık ki daha fazla veri sağlayamadım. Hesaplamalar ve yazılım kurulumu çok zaman almaktadır. Ancak, bu bilgi ilk analiz için yeterli olacaktır.
Veri analizi
Uzman Danışmanları test ettikten sonra bazı sonuçlar çıkarabiliriz:
- Global modelleri kullanan ve oldukça uzun vadede çalışabilen Uzman Danışmanlar, basit bir sayı brute force’u kullanılarak oluşturulabilir
- Gelecekteki çalışmanın süresi doğrudan veri örnekleminin büyüklüğüne bağlıdır
- Çalışma süresi doğrudan eğitim alanındaki test kalitesine bağlıdır
- İleri dönem için test yaparken, tüm grafiklerde global modellerin işlerliği en az 2-3 ay kalmaktadır
- En azından birkaç yıl daha çalışacak bir model bulma olasılığı, brute force bölümündeki nihai sonucun kalitesi %100'e eğilimli olduğunda artar
- Global modelleri aradığımızda, farklı ayarlar farklı döviz çiftleri için farklı şekilde çalışmaktadır
Bir ay gibi yerel modellere gelince, burada durum tamamen farklıdır. Bir önceki makalemde yerel modelleri analiz etmiştim, ancak programın bu sürümünde sunulan yeni fonksiyonları kullanmamıştım. Her türlü iyileştirme aynı konuların daha iyi anlaşılmasını sağlar. Yerel modellere gelince:
- Her zaman model değişimine dikkat etmelisiniz
- Martingale dikkatli bir şekilde kullanılabilir
Dolayısıyla, örneklem ne kadar büyük olursa, gelecekteki çalışabilirliğini o kadar uzun süre koruyacaktır. Ve tam tersi şekilde, örneklem ne kadar küçük olursa, model gelecekte o kadar hızlı tersine dönecektir (tabii ki, daha sonra eklemeyi planladığım ileri optimizasyon olmaması koşuluyla). Kısa bir aralık olması durumunda model terse dönüşü garantidir. Bu sonuçlara dayanarak, iki olası ticaret türü vardır:
- Global modellerden yararlanma
- Yerel modellerden yararlanma
İlk durumda, eğitim alanı ne kadar büyük olursa, model o kadar uzun süre çalışacaktır. Ancak yine de her 2 ila 3 ayda bir yeni formüller aramak daha iyidir. Yerel modeller söz konusu olduğunda, piyasa donmuş durumdayken her hafta arama yapılmalıdır. Sonuçların kalitesi yüksek olmayacaktır, ancak sonuç hakkında endişelenmenize de gerek yoktur - en azından biraz kâr elde edebileceksiniz.
Şimdi farklı ölçekli modeller üzerine yaptığım araştırmalar sonucunda elde ettiğim tüm verileri özetlemeye çalışacağım. Bunu yapmak için, belirli bir emrin beklenen getirisini (matematik beklentisi) yansıtan bir fonksiyonun yanı sıra kâr faktörünü yansıtan bir fonksiyon tanıtacağım. Daha az önemli ölçümleri karakterize eden başka fonksiyonlar da ekleyebilirsiniz. Olaylar uzayı veya rastgele bir değişken, gelecekteki olay gelişmelerinin tüm olası varyantları olacaktır. Şimdi sadece şunları biliyoruz:
- Gelecekteki "F"inci çubuk için sayısız olası gelişme vardır (üzerinde bir emir açılmış olsun ya da olmasın)
- Bir emrin belirli bir çubukta açıldığı gelecekteki gelişime yönelik tüm seçenekler için, bu emrin puan cinsinden bir beklenen getirisi ve bir kâr faktörü olacaktır (bir çubuk üzerinde bir test yaptığınızı düşünün, yalnızca sonraki çubuklar her emir için her zaman farklıdır)
- Tüm bu miktarlar her formül için farklı olacaktır
- Farklı gelecek başlangıç tarihlerine (geleceğin başlangıcı eğitim bölümünün sonudur) ve farklı eğitim bölümü sürelerine (eğitim bölümünün farklı başlangıç tarihlerine eşdeğerdir) sahip bölümler için, aranan son parametreler benzersiz değerler alacaktır
Tüm bu ifadeler matematiksel formüllere dönüştürülebilir. İşte formüller:
- MF = MF(T,I,F,S,R) - gelecekteki belirli bir çubuktaki emirlerin matematiksel beklentisi
- PF = PF(T,I,F,S,R) - gelecekteki belirli bir çubuktaki emirlerin kâr faktörü
- T - eğitim bölümünün süresi (bu durumda örneklem büyüklüğü veya çubuk sayısıdır)
- I - eğitim bölümünün bitiş tarihi
- F - eğitim bölümünün bitiş tarihinden başlayarak gelecekteki çubuk numarası
- S - benzersiz bir polinom veya bir algoritma (model manuel olarak veya başka bir Uzman Danışman tarafından bulunmuşsa)
- R - belirli bir polinom veya strateji (sinyal optimizasyonunun kalitesi) kullanılarak elde edilen sonuçlar; eğitim dönemindeki işlem sayısını ve matematiksel beklenti, kâr faktörü ve diğer parametreler gibi istenen ölçümleri içerir
Farklı enstrümanlar ve farklı tarihler üzerinde brute force’la elde edilen verilere dayanarak, yukarıdaki fonksiyonları bir grafik üzerinde çizebiliriz ("F" argüman olarak kullanılır):
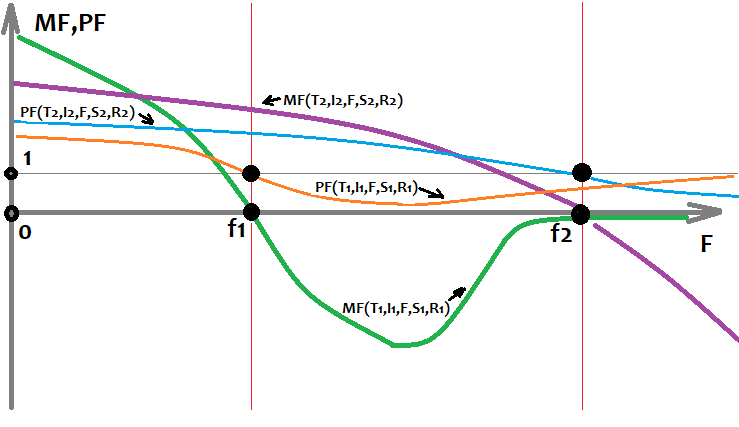
Bu grafik, farklı segmentlerde farklı ayarlar kullanılarak eğitilen ve farklı sonuçlar elde eden 2 benzersiz strateji varyantını göstermektedir. Bu tür sayısız seçenek vardır, ancak hepsi orijinal modelin süresi ve kalitesi açısından farklılık gösterir. Bunu her zaman bir model terse dönüşü takip eder. Bu kural sadece çok güçlü modeller için geçerli olmayabilir. Ancak onlar için bile grafiğin tersine dönme riski her zaman vardır, belki 5 yıl içerisinde ama tersine dönecektir. En istikrarlı formüller, en büyük örneklemden elde edilenler olacaktır. Formüller manuel olarak bulunursa ve bazı teorilerden kaynaklanırsa, gelecekte bu tür formüller süresiz olarak çalışabilir. Ancak, brute force veya diğer makine öğrenimi yöntemlerini kullanırken böyle bir garantimiz yoktur. Elimizdeki tek şey, yalnızca istatistiksel verilere dayanarak yapılabilecek bir çalışma süresi tahminidir. Bu analiz benim programımı kullanarak mümkündür, ancak sınırlı zaman ve hesaplama gücü nedeniyle tek bir kişi tarafından uygulanamaz.
Sırada ne var?
Global modellerin analizi, sıradan bir bilgisayarın gücünün 10 yıl veya daha uzun gibi büyük örneklemlerin derin ve yüksek kaliteli analizi için yeterli olmadığını göstermiştir. Her halükarda, yüksek kaliteli arama sonuçları elde etmek için çok büyük örneklemlerin analiz edilmesi gerekmektedir. Belki de programı birkaç ay boyunca yüksek performanslı bir sunucuda çalıştırırsak, bir veya iki iyi varyant bulabiliriz. Bu nedenle, brute force hızında bir artışla birlikte verimliliği de artırmamız gerekmektedir. Programın olası ileriki gelişimi aşağıdaki gibidir:
- Sabit sunucu zaman pencerelerini analiz etme yeteneğinin eklenmesi
- Haftanın belirli günlerinde analiz yapabilme yeteneğinin eklenmesi
- Rastgele zaman pencereleri oluşturma yeteneğinin eklenmesi
- Ticaret için haftanın izin verilen günlerinden oluşan bir diziyi rastgele oluşturma yeteneğinin eklenmesi
- Analizin ikinci aşamasının (optimizasyon sekmesi) iyileştirilmesi, özellikle çok çekirdekli hesaplamaların uygulanması ve optimizasyon hatalarının düzeltilmesi
Bu değişiklikler hem programın çalışma hızını hem de bulunan seçeneklerin değişkenliğini ve kalitesini büyük ölçüde artıracaktır. Ayrıca piyasa analizi için uygun bir araç takımı sağlamalıdırlar.
Değerlendirme
Umarım bu makale sizin için faydalı olur. Bana öyle geliyor ki makaledeki global modeller konusu çok önemlidir. Ancak, bunu yapmak benim için son derece zordu, çünkü programın yetenekleri bu tür bir analiz için hala yeterli değildir. Eğer 30 çekirdeğe erişimim olsaydı bu daha kolay olurdu. Analiz kalitesini artırmak için çok daha fazla zaman harcamamız gerekecektir.
Umarım gelecekte daha fazla hesaplama gücüne erişmek mümkün olur. Bir sonraki makalede devam edeceğiz. Ayrıca bu makalede, programı kullanırken ve manuel olarak model ararken ve onları optimize ederken faydalı olacak genel anlayış için bazı matematiksel ifadeler de sundum.
Makalenin genel ideali, henüz bu küçük sonuçları bile manuel olarak elde etmeyi başaramayanlara bilgi sağlamaktı. Robot geliştirirken kullanılan temel fikirlerin anlaşılmasına yardımcı olacaktır.
Bana öyle geliyor ki bir modeli nasıl bulduğumuz çok önemli değildir (manuel olarak veya bir yazılım kullanarak). Bir modelin bazı kârlı sonuçları varsa, onu çalışan bir model olarak kabul edebiliriz. Bazı model parametreleri bize bazı tahminler verir. Bu yakın geleceğe yönelik bir tahmin olabilir, ama yine de kâr etmek için yeterli olabilir. Ancak, bir model bulduysanız, bu aynı modelin gelecekte de çalışacağı anlamına gelmez. Bunu kontrol etmek için, örneklem boyunca çok iyi ticaret sonuçları olan ve örneklem büyüklüğü dikkate alındığında yeterli sayıda emir içeren çok büyük bir örnekleme ihtiyacınız olacaktır. Bir model bulmanın yanı sıra, başka bir sorun daha vardır - gelecekteki olası çalışma süresini tahmin etmek. Bence bu çok önemlidir. Ne kadar süre ve ne kadar iyi çalışacağını anlamadıktan sonra bir model bulmanın ne anlamı vardır? Programımı herkes kullanabilir. Makale ekinde mevcuttur. Özel kurulum soruları için lütfen bana özel mesaj gönderin.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/8660
 Model aramada brute force yaklaşımı (Bölüm III): Yeni ufuklar
Model aramada brute force yaklaşımı (Bölüm III): Yeni ufuklar
 Ticaret sistemlerinin geliştirilmesi ve analizi için optimum yaklaşım
Ticaret sistemlerinin geliştirilmesi ve analizi için optimum yaklaşım
 Otomatik ticaret için faydalı ve ilginç teknikler
Otomatik ticaret için faydalı ve ilginç teknikler
 Grid ve martingale: bunlar nedir ve nasıl kullanılır?
Grid ve martingale: bunlar nedir ve nasıl kullanılır?
- Ücretsiz ticaret uygulamaları
- 24 saat boyunca ücretsiz Forex VPS
- Ticaret kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Web sitesi politikasını ve kullanım şartlarını kabul edersiniz