Model aramada brute force yaklaşımı (Bölüm IV): Asgari işlevsellik

Bu makalede, programımın asgari işlevselliği kazanmış ve ticaret için çalışan ayarlar üretebilen yeni bir sürümünü sunacağım. Değişiklikler öncelikle kullanım kolaylığını artırmayı ve minimum giriş eşiğini iyileştirmeyi amaçlamaktadır. Ana hedef hala olabildiğince çok kullanıcıyı ayarlar ve piyasa araştırması arayışına çekmektir. Ticaret detaylarını tartışmak yerine, mümkün olduğunca faydalı bilgiler vereceğim. Bu yöntemin nasıl kullanılacağına dair anlaşılır bir açıklama sunmaya, avantaj ve dezavantajları tanımlamaya ve pratik uygulama beklentilerini değerlendirmeye çalışacağım.

• Yeni sürümdeki değişiklikler
  
• İlk gösterim ve yeni konsept
• Değiştirilmiş Fourier serisine dayalı yeni polinom
• İçeriden yazılım uygulaması hakkında
• Makas gürültüsüyle mücadele ve makasın muhasebeleştirilmesi için yeni mekanizma
• Kısa alanlarda lot varyasyonu
• Global geçmiş üzerinde çalışan varyantlar
• Brute force matematiği
• Geçmişe takılı kalmak ve aşırı uyum üzerine
• Kullanım önerileri
• Sonuç
• Serinin önceki makalelerine linkler

Yeni sürümdeki değişiklikler

Bir önceki makalede olduğu gibi, program işlevsellik ve kullanılabilirlik açısından önemli ölçüde geliştirilmiştir. Önceki sürümler oldukça kullanışsızdı ve çeşitli hatalar içeriyordu. Bu sürüm çok sayıda değişiklik içermektedir. Uzman Danışman şablonlarını ve yazılımı modernize etmek için çok şey yapıldı. Değişikliklerin listesi:

1. Yeniden tasarlanmış arayüz
2. Brute force için başka bir polinom eklendi (revize edilmiş Fourier serisine dayalı)
3. Rastgele sayı üretmek için geliştirilmiş mekanizma
4. Yöntem konsepti kullanım kolaylığı açısından iyileştirildi
5. Ultra kısa alanlar için lot varyasyonu mekanizmaları eklendi
6. Makas hesaplama mekanizması eklendi
7. Makas gürültüsünü azaltmak için bir mekanizma eklendi
8. Hata düzeltmeleri

Daha önce planlanan değişikliklerin çoğu hayata geçirilmiştir. Gelecekte de algoritma değişiklikleri yapılacaktır, ancak onlar bu kadar önemli olmayacaktır.

İlk gösterim ve yeni konsept

Uzman Danışmanlar oluştururken, her zaman Uzman Danışman adları oluşturmanın ve çok sayıda ayarla uğraşmanın zor olabileceğini fark ettim. Bazen adlar çakışabilir ve ayarlar karıştırılabilir. Bu sorunun çözümü, ayarları alan bir Uzman Danışmandır. Program, normal txt biçiminde bir yapılandırma dosyası oluşturabilir ve Uzman Danışman bunu okuyacaktır. Bu yaklaşım, bu çözümle çalışmayı hızlandırır ve onu daha basit ve anlaşılır hale getirir. Çözüm şeması şimdi şu şekilde görünmektedir:

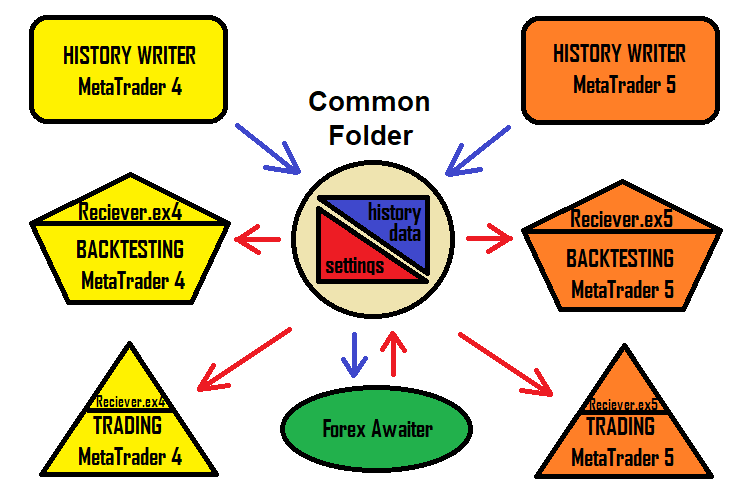
Elbette, programın robot üreten sürümü hala mevcuttur. Ancak bu makale, spesifik olarak MetaTrader 4 ve MetaTrader 5 terminalleri için icat edilmiş yeni bir konsepte sahiptir - bu konsept, sıradan kullanıcıların bu çözümü olabildiğince basit ve hızlı bir şekilde kullanmaya başlamasına olanak tanır. Bu çözümle ilgili en kullanışlı kısım, ayarın MetaTrader 4 ve MetaTrader 5'te aynı şekilde çalışmasıdır.

Yeni arayüzün sadece bir kısmını göstereceğim, çünkü oldukça büyüktür ve dolayısıyla makalede çok fazla yer kaplayacaktır. Yalnızca ilk sekmeyi göstereceğim:

Kolay gezinme için tüm öğeler ilgili bölümlere ayrılmıştır. Kullanılmayan öğeler, kullanımları anlamsızsa engellenir.

Programın çalışmasını gösteren özel bir video hazırladım:

Ayarları sıradan ayar dosyaları aracılığıyla iletmek neden mümkün değildir? Bunun nedeni, ayar dosyalarının diziler içerememesidir, ancak bu yöntemin ise değişken uzunluğa sahip girdiler şeklinde diziler kullanmasıdır. Bu durumda en uygun çözüm sıradan metin dosyalarını kullanmaktır.

Değiştirilmiş Fourier serisine dayalı yeni polinom

Makine öğrenimine aşina olan birçok kişi, algoritmaları için Fourier serisini farklı amaçlarla aktif olarak kullanmaktadır. Fourier serisi başlangıçta bir fonksiyonu [-π; π] aralığında bir seriye ayrıştırmak için oluşturulmuştur. Bilmemiz gereken şey, fonksiyonun bir seriye nasıl ayrıştırılacağı ve böyle bir ayrıştırmanın gerekli olup olmadığıdır. Buna ek olarak, değişken değiştirme yönteminin özelliklerini bilmek önemlidir, çünkü ayrıştırma [-π; π] aralığında değil, farklı bir aralıkta gerçekleştirilebilir. Tüm bunlar, iyi bir matematik bilgisinin yanı sıra, bunu ticaret için kullanmanın herhangi bir anlamı olup olmadığının anlaşılmasını gerektirir. Fourier serisinin genel görünümü aşağıdaki gibidir:

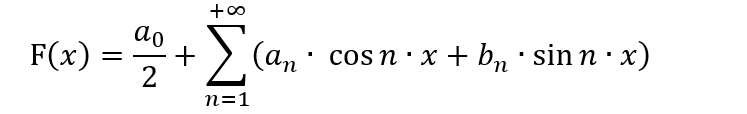
Bu formda, bu polinom yalnızca ticaret modellerini daha uygun bir biçimde sunmak ve fiyatın bir dalga süreci olduğunu varsayarak fiyat hareketini tahmin etmeye çalışmak için yararlı olabilir. Bu varsayım geçerli gibi görünmektedir, ancak bu haliyle brute force için uygulanamaz, çünkü bu durumda yöntemin tüm konseptini kökten değiştirmemiz gerekecektir. Bunun yerine, polinomu bu yöntem için uygulanabilecek şekilde dönüştürmemiz gerekir. Çok fazla varyasyon olabilir. Ancak, formülü amacına uygun olarak kullanmadan Fourier serisine yakın tutmak için aşağıdaki gibi yapmayı öneriyorum:

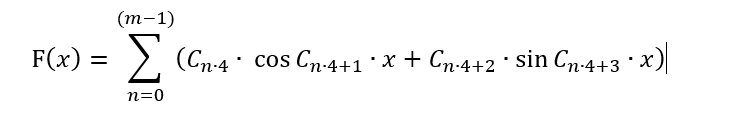
Burada serinin daha fazla özgürlüğe sahip olması dışında hiçbir şey değişmedi: periyodu hem artı hem de eksi olarak dalgalanmaktadır. Ayrıca, artık sınırlı sayıda terim var. Bunun nedeni, C[] dizisinin uygun bir formül bulmak için birleştireceğimiz katsayıları içermesidir. Bu tür katsayıların sayısı sınırlıdır. Bu seri sonsuz olamaz, bu yüzden onu "m" çubukla sınırlamamız gerekir. Ayrıca, simetriyi korumak için ilk terimi kaldırdım, böylece formül değerleri "+" ve "-" aralıklarında en simetrik sinyalleri üretecektir. Ancak bu şekilde sadece 1 çubuğa bağlı olarak bir fonksiyon seçebiliriz! Tüm çubuk değerlerinin formülde mevcut olduğundan emin olmalıyız. Ayrıca, bir çubuğun 1 değil 6 parametresi vardır. Bu 6 parametre bu serinin ikinci makalesinde ele alınmıştır. Burada, geri kalan tüm çubukları hesaba katabilmek adına tek çubuk işleme hassasiyetini feda etmemiz gerekiyor. İdeal olarak, bu miktar bir diğerine sarılmalıdır. Ancak polinomu karmaşıklaştırmak istemiyorum ve bu nedenle şimdilik en basit versiyonunu kullanacağız:

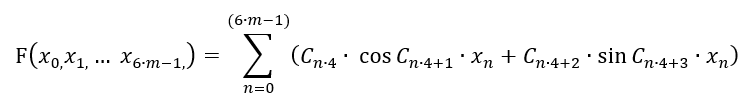
Aslında tek boyutlu bir fonksiyon çok boyutlu bir fonksiyona dönüşmüştür. Ancak bu, bu polinomun seçilen çok boyutlu hiperküpte herhangi bir çok boyutlu fonksiyonu tanımlayabileceği anlamına gelmez. Her halükarda, bu fonksiyon Taylor serileri tarafından düzgün bir şekilde kapsanamayan diğer modelleri tanımlayabilen başka bir çok boyutlu fonksiyon ailesi sağlar. Bu, aynı veri örneklemi üzerinde daha iyi bir model bulma şansı tanır. 

Kodda bu fonksiyon şu şekilde görünecektir:

if ( Method == "FOURIER" )
   {
      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(Close[i+1]-Open[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Close[i+1]-Open[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(High[i+1]-Open[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(High[i+1]-Open[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(Open[i+1]-Low[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Open[i+1]-Low[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(High[i+1]-Close[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(High[i+1]-Close[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(Close[i+1]-Low[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Close[i+1]-Low[i+1])/_Point);
         iterator+=4;
         }         

   return Val;
   }

Bu, fonksiyonun tamamı değil, sadece polinomu uygulayan kısmıdır. Basitliğine rağmen, bu tür formüller bile piyasaya uyarlanabilir.

Bu formülün işe yarayabileceğini göstermek için bu yöntemi kullanarak geçen yıla ait geçmiş veriler için çok hızlı bir brute force gerçekleştirdim. Ancak, iyi çalışıp çalışmadığını öğrenmemiz gerekecek. Aslında, bu formülü kullanarak gerçekten etkili bir çözüm bulmayı başaramadım. Ancak bunun bir zaman ve hesaplama kapasitesi meselesi olduğunu düşünüyorum. İlk versiyonla çalışmak için çok zaman harcadım. Bu, son yıl üzerinde USDJPY M15 için elde etmeyi başardığım sonuçtur:

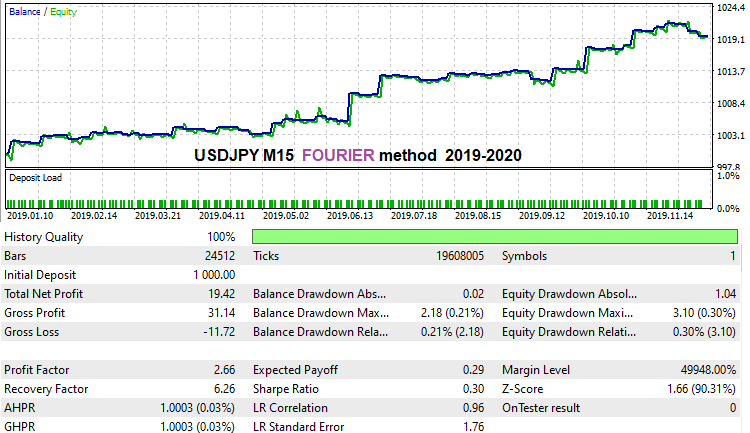
Bu formülde hoşuma gitmeyen şey, makas gürültüsünü bastırma açısından çok dengesiz olmasıdır. Belki de bu, bu yöntem çerçevesinde harmonik fonksiyonların özellikleriyle bağlantılıdır. Belki de formülü tam olarak doğru formüle edemedim. İkinci sekmedeki "Spread Control" seçeneğini etkinleştirdiğinizden emin olun. Bu, optimizasyon sırasında makas gürültüsünü bastırma mekanizmasını devre dışı bırakacak ve oldukça iyi varyantlar üretecektir. Muhtemelen formül çok "nazik"tir. Yine de oldukça iyi varyantlar bulabiliyor.

İçeriden yazılım uygulaması hakkında

Bu konuya önceki makalelerimde çok az yer vermiştim. İçeriden nasıl çalıştığını göstermek için bu bölümü yazmaya karar verdim. En ilginç ve kolay kısım, formül için katsayıların oluşturulmasıdır. Bu kısmın açıklanması, katsayıların nasıl oluşturulduğunun anlaşılmasına yardımcı olabilir:

public void GenerateC(Tester CoreWorker)
   {
   double RX;
   TYPE_RANDOM RT;
   RX = RandomX.NextDouble();
   if (RandomType == TYPE_RANDOM.RANDOM_TYPE_R) RT = (TYPE_RANDOM)RandomX.Next(0, Enum.GetValues(typeof(TYPE_RANDOM)).Length-1);
   else RT = RandomType;

   for (int i = 0; i < CoreWorker.Variant.ANum; i++)
      {
      if (RT == TYPE_RANDOM.RANDOM_TYPE_0) 
         {
         if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i-1]*RandomX.NextDouble();
         else CoreWorker.Variant.Ci[0]=1.0;
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_5)
         {
         if (RandomX.NextDouble() >= 0.5)
            {
            if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i - 1] * RandomX.NextDouble();
            else CoreWorker.Variant.Ci[0] = 1.0;
            }
         else
            {
            if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i - 1] * (-RandomX.NextDouble());
            else CoreWorker.Variant.Ci[0] = -1.0;
            }
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_1) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
      if (RT == TYPE_RANDOM.RANDOM_TYPE_2)
         {
         if (RandomX.NextDouble() >= 0.5) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
         else CoreWorker.Variant.Ci[i] = -RandomX.NextDouble();
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_3)
         {
         if (RandomX.NextDouble() >= RX)
            {
            if (RandomX.NextDouble() >= RX + (1.0 - RX) / 2.0) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
            else CoreWorker.Variant.Ci[i] = -RandomX.NextDouble();
            }
         else CoreWorker.Variant.Ci[i] = 0.0;
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_4)
         {
         if (RandomX.NextDouble() >= RX) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
         else CoreWorker.Variant.Ci[i] = 0.0;
         }
      }
   }

Oldukça basittir: rastgele sayı üretimi için birkaç sabit tür vardır ve her şeyi aynı anda uygulayan genel bir tür vardır. Üretim türlerinin her biri pratikte test edilmiştir. "RANDOM_TYPE_R" genel üretim türünün maksimum verimliliği gösterdiği ortaya çıktı. Sabit türler, farklı enstrümanlar ve zaman dilimlerindeki fiyatların farklı doğası nedeniyle her zaman bir sonuç vermemektedir. Görsel olarak çoğu durumda bu farklılıklar görülemez, ancak makine her şeyi görür. Bazı zaman dilimlerindeki bazı sabit türler maksimum kalitede daha fazla sinyal sağlayabilir. Örneğin, NZDUSD H1'de, RANDOM_TYPE_4, yani "sadece sıfırlar ve pozitif sayılar" kullanıldığında sonuçların kalitesinde keskin bir artış olduğunu fark ettim. Bu, gözle görülemeyen gizli dalga süreçlerinin net bir işareti olabilir. Farklı enstrümanları daha detaylı incelemek isterdim ama bunu tek başıma yapmak zor.

Makas gürültüsüyle mücadele ve makasın muhasebeleştirilmesi için yeni mekanizma

Önceki makalede belirtildiği gibi, makas fiyat verilerini bozar, böylece bulunan modellerin çoğu çoğunlukla makas içerisinde yer alır. Makas, herhangi bir stratejinin en büyük düşmanıdır, çünkü çoğu strateji, makası karşılamak için yeterli matematiksel beklenti sağlayamaz. Bir gerçek hesapta bir ay veya hatta bir yıl boyunca yapılan geriye dönük teste veya pozitif ticaret istatistiklerine aldanmamalısınız, çünkü bu veri örneklemi gelecekteki performansı değerlendirmek için çok küçüktür. “Gece scalper’ları” adı verilen ayrı bir ticaret stratejileri ve otomatik ticaret sistemleri sınıfı vardır. Bu robotlar sınırlı bir süre içerisinde küçük kârlar yakalar. Brokerlar, gece yarısından sonra makasları genişleterek bu tür sistemlerle aktif olarak mücadele etmektedir. Makas, çoğu stratejinin kâr sağlayamayacağı bir seviyede belirlenmiştir.

Çoğu broker için neredeyse aynı olan bir değer vardır:

• Spread = (Ask-Bid)/_Point
• MidPrice = (Ask+Bid)/2

Bu fiyat yeşil renkle vurgulanmıştır. Bu, emir defterinin ortasıdır. Emir defteri genellikle bu fiyata göre sıralanır ve her iki fiyat da bu fiyattan eşit uzaklıktadır. Aslında, emir defterinin klasik tanımına bakarsak, bu fiyat hiçbir anlam ifade etmez çünkü orada hiçbir ticaret emri yoktur. Tüm brokerların kendi makasları olduğunu varsaysak bile, bu fiyat tüm brokerlar için neredeyse aynı olabilir. Bu durumu bir diyagramda çizeyim:

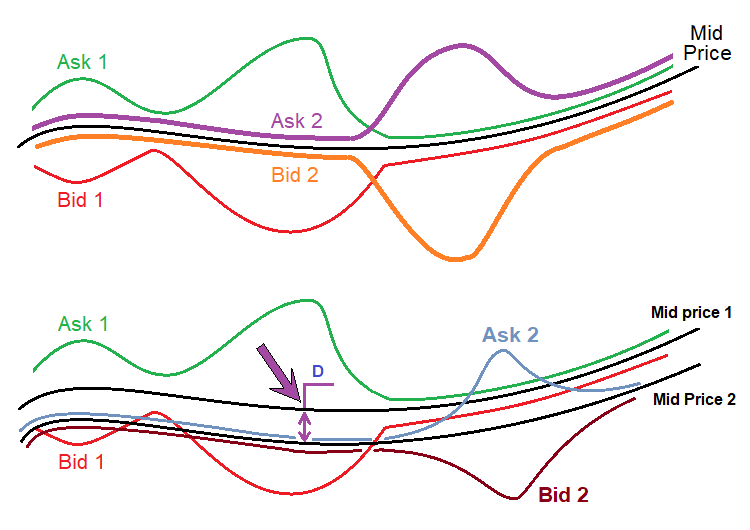
Üstteki şekilde rastgele seçilen iki brokerın fiyat serileri gösterilmektedir. Her zaman alış ve satış fiyatlarını simgeleyen bir "Ask" fiyatı ve bir "Bid" fiyatı vardır. Siyah çizgi her iki fiyat serisi için de aynıdır. Bu fiyat yukarıda gösterdiğim gibi kolayca hesaplanabilir. En önemli şey, bu değerin pratikte belirli bir brokerın genişleyen veya daralan makaslarına bağlı olmamasıdır, çünkü tüm değişiklikler ilgili fiyata göre neredeyse eşittir.

Alttaki şekil, farklı brokerlardan gelen fiyatlarla gerçekleşen gerçek bir durumu göstermektedir. Mesele şu ki, bu ortalama fiyat bile farklı akışlarda farklıdır. Bunun nedenlerini şahsen bilmiyorum. Bilseydim bile, ticaret için pek faydası olmazdı. Bu gerçeği, tüm bu nüansların son derece önemli olduğu arbitraj ticareti yaparken keşfettim. Bizim yöntemimizle ilgili olarak, yalnızca şu önemlidir:

• MidPrice1 = f(t)
• MidPrice2 = MidPrice1-D
• MidPrice1 '(t) = MidPrice2 '(t)

Başka bir deyişle, her iki fiyat serisinin ortalama fiyatı (zaman fonksiyonları olarak gösterilirse) aynı türeve sahiptir, çünkü bu fonksiyonlar sadece "D" sabitinde farklılık gösterir. Polinomumuz fiyatları değil farklarını kullandığından, tüm değerler bu ortalama fiyat fonksiyonlarının türevlerinin fonksiyonelleri olacaktır. Bu türevler tüm brokerlar için aynı olduğundan, ayarların farklı brokerlarla verimli olabileceğini bekleyebiliriz. Alternatif olarak, eğer bulduğumuz ayarlar bir brokerda gerçek tikler üzerinde geriye dönük testte başarısız olursa, buna bağlı olarak ayarlarımızın başka bir brokerda da uygulanabilir olma şansı düşük olacaktır.

Bu mekanizmayı uygulayabilmek için çözümün tüm unsurlarında uygun değişiklikler yapmam gerekti. İlk olarak, fiyat dosyasını yazarken çubuğun tüm önemli noktalarındaki makasları kaydetmek gerekir. Bunlar Open[], Close[], High[] ve Low[] noktalarıdır. Çubuklar Bid fiyatlarına dayandığından, değerleri ayarlamak ve böylece Ask fiyatını elde etmek için makas kullanılacaktır. Fiyat yazan Uzman Danışmanlar artık çubuklara değil tiklere dayanmaktadır. Bu çubukları kaydetme fonksiyonu şimdi aşağıdaki gibi görünmektedir:

void WriteBar()
   {
   FileWriteString(Handle0x,"\r\n");
   FileWriteString(Handle0x,DoubleToString(Close[1],8)+"\r\n");
   FileWriteString(Handle0x,DoubleToString(Open[1],8)+"\r\n");
   FileWriteString(Handle0x,DoubleToString(High[1],8)+"\r\n");
   FileWriteString(Handle0x,DoubleToString(Low[1],8)+"\r\n");         
   FileWriteString(Handle0x,IntegerToString(int(Time[1]))+"\r\n");
   FileWriteString(Handle0x,IntegerToString(PrevSpread)+"\r\n");
   FileWriteString(Handle0x,IntegerToString(CurrentSpread)+"\r\n");
   FileWriteString(Handle0x,IntegerToString(PrevHighSpread)+"\r\n");
   FileWriteString(Handle0x,IntegerToString(PrevLowSpread)+"\r\n");   
   MqlDateTime T;
   TimeToStruct(Time[1],T);
   FileWriteString(Handle0x,IntegerToString(int(T.hour))+"\r\n");
   FileWriteString(Handle0x,IntegerToString(int(T.min))+"\r\n");
   FileWriteString(Handle0x,IntegerToString(int(T.day_of_week))+"\r\n");         
   }      

Dört satır yeşil renkle vurgulanmıştır - bu satırlar çubuğun dört noktasındaki makası kaydeder. Önceki sürümde bu değerler kaydedilmiyordu ve hesaplamalarda dikkate alınmıyordu. Bu veriler kolayca elde edilebilir ve kaydedilebilir. Aşağıdaki basit tik tabanlı fonksiyon, Yüksek ve Düşükteki makası elde etmek için kullanılır:

void RecalcHighLowSpreads()
   {
   if ( Close[0] > LastHigh )
      {
      LastHigh=Close[0];
      HighSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD));
      }
   if ( Close[0] < LastLow )
      {
      LastLow=Close[0];
      LowSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD));
      }      
   }

Bu fonksiyon yalnızca mevcut çubuk oluşturulurken çubuğun Yüksek ve Düşük noktasındaki makası belirler. Yeni bir çubuk göründüğünde, mevcut çubuğun tamamen oluştuğu kabul edilir ve verileri dosyaya yazılır. Bu fonksiyon başka bir çubuk tabanlı fonksiyonla birlikte çalışır:

bool bNewBar()
   {
   ArraySetAsSeries(Close,false);                        
   ArraySetAsSeries(Open,false);                           
   ArraySetAsSeries(High,false);                        
   ArraySetAsSeries(Low,false);                              
   CopyOpen(_Symbol,_Period,0,2,Open);
   CopyClose(_Symbol,_Period,0,2,Close);
   CopyHigh(_Symbol,_Period,0,2,High);
   CopyLow(_Symbol,_Period,0,2,Low);
   ArraySetAsSeries(Close,true);                        
   ArraySetAsSeries(Open,true);                           
   ArraySetAsSeries(High,true);                        
   ArraySetAsSeries(Low,true);                                 
   if ( Time0 < Time[1] )
      {
      if (Time0 != 0)
         {
         Time0=Time[1];
         PrevHighSpread=HighSpread;
         PrevLowSpread=LowSpread;         
         PrevSpread=CurrentSpread;
         CurrentSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD));
         HighSpread=CurrentSpread;
         LowSpread=CurrentSpread;         
         return true;
         }
      else
         {
         Time0=Time[1];
         return false;
         }
      }
   else return false;
   }

Bu fonksiyon hem bir dayanak fonksiyonudur hem de dört makasın tamamının nihai olarak belirlendiği mantığın önemli bir unsurudur. Benzer şekilde program içerisinde de uygulanır. OnTick işleyicisinde çok basit bir şekilde çalışır:

RecalcHighLowSpreads();
if ( bNewBar()) WriteBar();

Fiyat dosyası aşağıdaki verileri içerecektir:

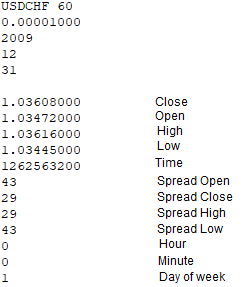
Ortalama fiyatları içeren dizi, program içerisinde aynı şekilde uygulanır:

OpenX[1]=Open[1]+(double(PrevSpread)/2.0)*_Point;
CloseX[1]=Close[1]+(double(Spread)/2.0)*_Point;
HighX[1]=High[1]+(double(PrevHighSpread)/2.0)*_Point;
LowX[1]=Low[1]+(double(PrevLowSpread)/2.0)*_Point;

Bu yaklaşımın makas gürültüsünün bastırılması için kullanılabileceği düşünülebilir. Ancak sorun, belirli sayıda toplanmış tik gerektirmesidir (zaman dilimi ne kadar yüksekse, çubuk başına o kadar fazla tik gerekir). Çok sayıda tikin toplanması çok zaman gerektirir. Ayrıca, çubuklar Ask fiyatlarını veya makas değerlerini saklamaz, bu nedenle hesaplamalar için Bid'i kullandık.

Ek bir seçenek olarak, sonuçları optimize ederken makası dikkate almak için bir mekanizma ekledim. Testler, bu mekanizmanın isteğe bağlı olduğunu, ancak yeterli hesaplama gücüyle oldukça iyi sonuçlar verebileceğini gösterdi. Buradaki fikir, algoritmanın yalnızca makas gerekli değeri aşmadığında emirleri açmasını ve kapatmasını gerektirmektir. Mevcut sürüm, makası çubuk verilerine kaydeder, böylece değer kontrol edilebilir ve makas hariç gerçek test değerlerini hesaplamamıza olanak tanır.

Kısa alanlarda lot varyasyonu

Lot varyasyonu (çeşitlerinden biri) sadece çok kısa alanlarda değil, aynı zamanda uzun alanlarda da kullanılabilir. İki risk/lot yönetim mekanizması bulunmaktadır.

• Lotu artırma
• Lotu azaltma

İlk mekanizma, sinyalin yakında tersine dönmesini beklediğimizde tersine çevrilmiş ticarette kullanılmalıdır. İkinci seçenek yalnızca sinyalin stabil olduğu ve uzun süre devam edeceği biliniyorsa işe yarar. Herhangi bir kontrol fonksiyonunu kullanabilirsiniz. Ben en basit olanları kullandım - doğrusal fonksiyonlar. Başka bir deyişle, lot zaman içerisinde değişir. Mekanizmanın işleyişini pratikte görelim.

Bu, USDJPY M15 fiyatı kullanılarak yapılacaktır. Bu durumda, robotun MQL4 versiyonunu gösterme amaçlı kullanıyorum, çünkü robot artan makas noktalarında ticaret yaptığı için gerçek tikler üzerinde geriye dönük testlerde başarısız olmaktadır. Düşük zaman dilimlerinde iyi bir brute force yaklaşımının, brute force’un süresine eşit veya daha büyük bir aralıkta iyi ileriye dönük sonuçlar sağlayabileceğini kanıtlamak istedim. Bilgisayar kapasitem sınırlı olduğu için çalışmayı çok geniş gerçekleştiremedim. Ancak bu, iki lot yönetim mekanizmasını açıklamak için yeterli olacaktır. Arama aralığında bulunan varyant ile başlayalım. Aralık bir yıla eşittir:

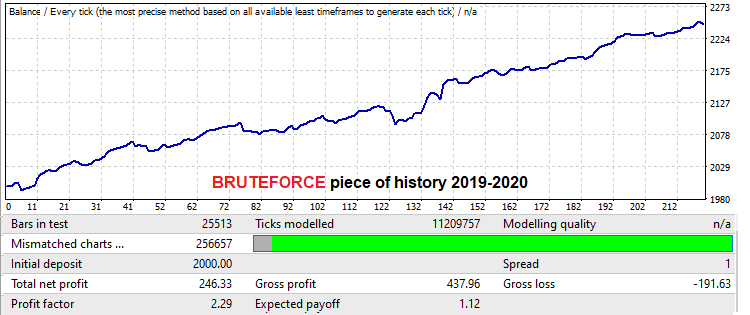
Buradaki matematiksel beklenti 12 puandan biraz daha fazladır (bu sefer makas olmadan, ki bu bizim için önemli değildir çünkü bu sefer makası göz ardı ediyoruz). Kâr faktörüne bakacağız. Bir yıllık ileriye dönük test aşağıdaki gibidir:

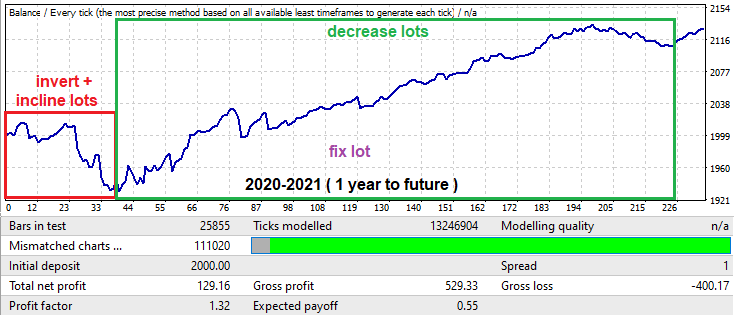
Arama sadece bir yıl sürmesine rağmen, en az bir yıl boyunca çalışmaya devam etti. Pratikte bu, iyi bir bilgisayarınız varsa, bir veya iki hafta içinde düşük makaslı tüm ana döviz çiftlerini analiz edebileceğiniz, ardından en iyilerini seçebileceğiniz ve en az bir yıl daha modelden yararlanabileceğiniz anlamına gelir. Sistemin MetaTrader 5'te gerçek tikler üzerindeki geriye dönük testi geçtiğinden emin olmayı unutmayın. Daha fazla kanıt elde etmek için, sonuçları toplamak ve istatistikleri derlemek amacıyla birkaç bilgisayarda verileri analiz etmek üzere küçük bir ekibe katılmak iyi bir fikirdir.

Şimdi ileri teste bakalım - başlangıçta çok büyük bir düşüş (drawdown) vardır, bu genellikle bir yıl gibi küçük zaman aralıklarında modeller aradığımızda çok yaygındır. Bununla birlikte, bu düşüş bile kendi amaçlarımız için kullanılabilir. Bu aralık yukarıdaki grafikte kırmızı çerçeve içerisinde gösterilmektedir. Buradaki Uzman Danışman çalışma süresi ayarlarda 50 işlem günü ile sınırlıdır (cumartesi ve pazar günleri sayılmaz). Ayrıca, düşüşü kâra dönüştürmek için sinyal ters çevrildi. Bunu, terse çevrildikten sonra negatife dönüşeceği için düşüşten sonraki grafik kısmını kesmek için yaptım. Ortaya çıkan geriye dönük test aşağıdaki gibidir:

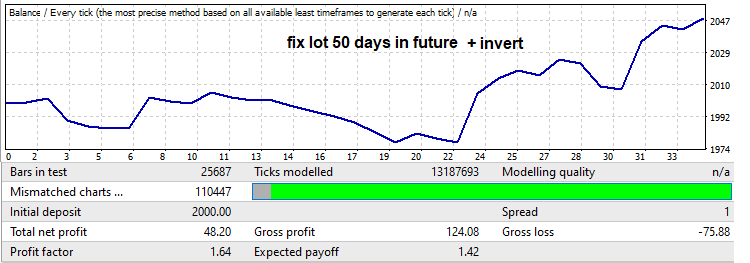
Kâr faktörüne dikkat edin. Onu artıracağız. Bir geri çekilmenin olup olmayacağını ve bu geri çekilmenin ne kadar ileri gideceğini asla bilemezsiniz, ancak genellikle brute force segmentinde meydana gelen hareketin oldukça büyük bir kısmı kadar geri çekilir. Minimumdan maksimuma doğrusal bir lot artışı uygulayarak, böyle bir geriye dönük test ve kâr faktöründe bir artış elde edeceğiz:

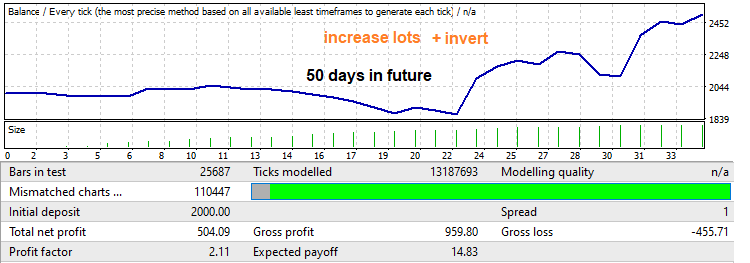
Şimdi de bir yıllık ileriye dönük testte yeşil çerçeve içerisinde gösterilen mekanizmayı görelim. Bu kısım, büyük bir büyüme ve ardından modelin tersine döndüğünü göstermektedir. Bu durumda lot azaltma yöntemini kullanacağız. Robot, bu segmentin sonuna kadar ticaret yapmaya ayarlanmıştır. İlk olarak, sonuçları daha sonra karşılaştırabilmek adına sabit bir lot ile test edelim:

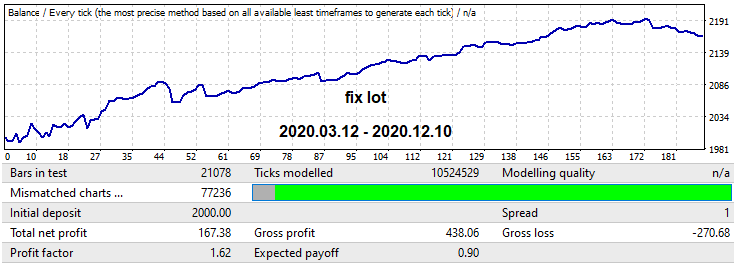
Şimdi zaman içerisinde lot düşüşü uygulayan mekanizmayı etkinleştirelim. Bu aynı zamanda kâr faktöründe bir artışa neden olurken, grafik daha yumuşak hale gelir ve sonunda düşüş olmaz:

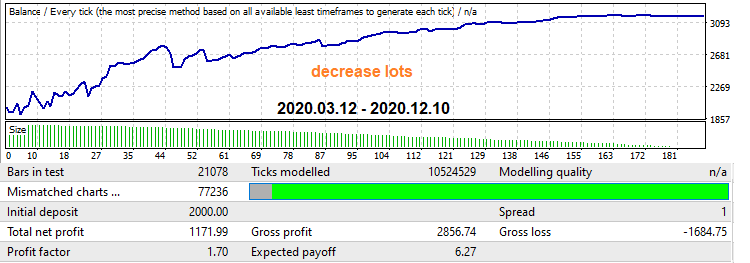
Birçok Mağaza satıcısı bu teknikleri kullanır. Doğru zamanda ve doğru yerde uygulandıklarında, hem kârlılığı artırabilir hem de zararları azaltabilirler. Ancak pratikte durum daha karmaşıktır. Bu mekanizmalar programım tarafından oluşturulan Uzman Danışmanlarda sağlanmıştır, böylece gerektiğinde onları etkinleştirebilir ve devre dışı bırakabilirsiniz.

Global geçmiş üzerinde çalışan varyantlar

Birçok okuyucunun, gerçek tik geçmişi üzerinde global geriye dönük testleri geçebilen çalışan ayarlara sahip bazı varyantlar görmek ve kontrol etmek isteyeceğini düşünüyorum. Böyle ayarlar buldum. Sınırlı hesaplama kapasitesi nedeniyle ve tek başıma brute force uyguladığım için arama oldukça uzun sürdü. Ancak yine de birkaç varyant bulmayı başardım. Bunlar, şu şekildedir:

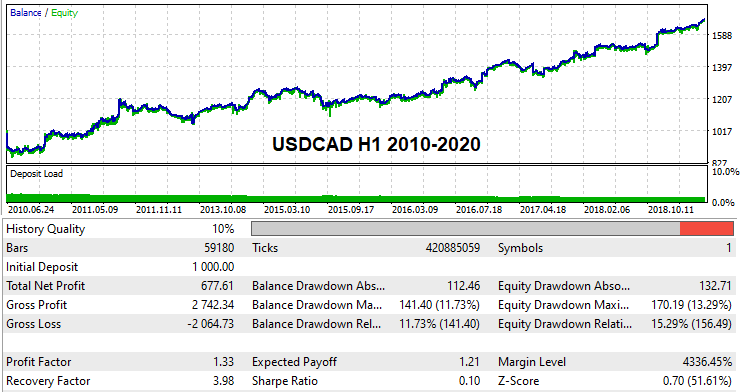
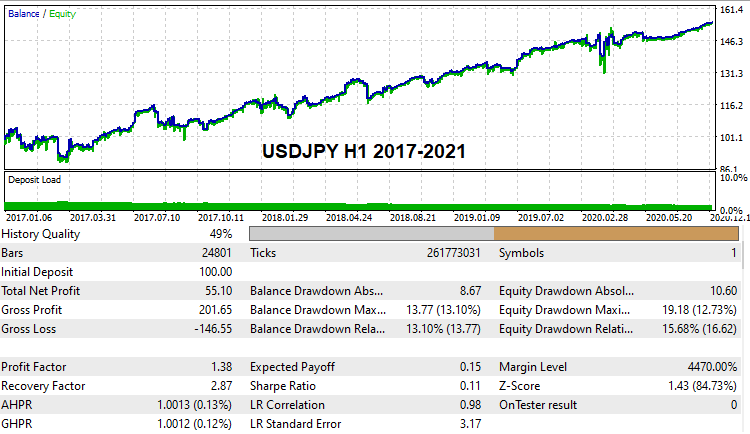
Bu ayarlar aşağıda eklenmiştir, böylece dilerseniz test edebilirsiniz. Ayrıca kendi ayarlarınızı bulmaya çalışabilir ve onları demo hesaplarda geriye dönük olarak test edebilirsiniz. Programın bu sürümünden itibaren herkes bu yöntemi deneyebilir.

Brute force matematiği

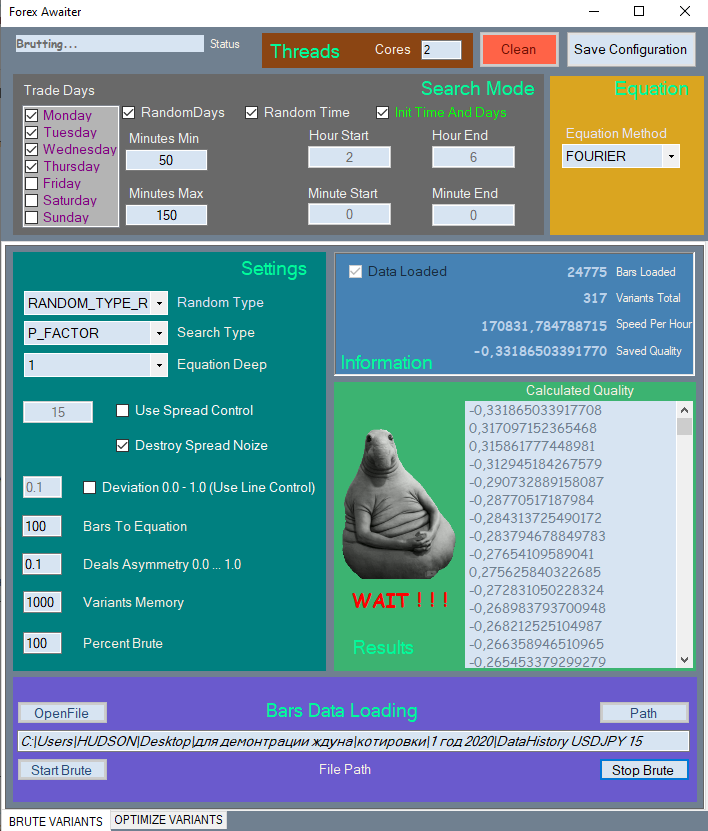
Bu bölüm, kullanıcıların altta yatan hesaplama ilkelerini anlamalarına yardımcı olmak için kapsamlı bir açıklamaya ihtiyaç duymaktadır. Programın ilk sekmesinin nasıl çalıştığı ve sonuçlarının nasıl yorumlanacağı ile başlayalım.

İlk sekmede brute force

Aslında, herhangi bir brute force algoritmasında gerçekleşen her şey her zaman olasılık teorisiyle bağlantılıdır, çünkü her zaman bir modelimiz ve bir yinelememiz vardır. Buradaki bir yineleme, mevcut strateji varyantının analizinin tam bir döngüsüdür. Tam bir döngü, özel yaklaşıma bağlı olarak bir veya birden fazla testten oluşabilir. Testlerin ve diğer manipülasyonların sayısı çok önemli değildir çünkü her şey bir yineleme olarak sınıflandırılabilir. Bir yineleme, sonuca yönelik gereksinimlere bağlı olarak başarılı veya başarısız olarak değerlendirilebilir. Analiz yöntemine bağlı olarak çok çeşitli nicel değerler iyi bir sonuç için kriter olarak kullanılabilir.

Algoritma her zaman gereksinimlerimize uygun bir veya daha fazla varyant çıkarır. Algoritmaya bellekte ne kadar sonuç depolanması gerektiği konusunda talimat verebiliriz. Gereksinimi karşılayan ancak depolama alanına sığmayan diğer tüm sonuçlar atılacaktır. Brute force algoritmamızda kaç adım olursa olsun, bu işlem her zaman gerçekleşecektir. Aksi takdirde, kasıtlı olarak düşük kaliteli verileri işlemek için çok fazla zaman harcayacağız. Bu şekilde, tek bir varyant bile kaybolmaz, ancak bu, arama hızını düşürebilir. Hangi yaklaşımı kullanacağınız nihayetinde size bağlıdır.

Şimdi doğrudan konuya girelim. Herhangi bir sonuç arama süreci nihayetinde Bernoulli şemasına göre bağımsız testler sürecine indirgenir (algoritmanın sabit olması koşuluyla). Her şey iyi bir varyant elde etme olasılığına bağlıdır. Bu olasılık sabit bir algoritma için her zaman sabittir. Bizim durumumuzda bu olasılık aşağıdaki değerlere bağlıdır:

• Örneklem büyüklüğü
• Algoritma değişkenliği
• Tabana yakınlık
• Nihai sonuç için gereksinimlerin katılığı

Bu bağlamda, elde edilen sonuçların miktarı ve kalitesi Bernoulli formülüne göre yineleme sayısı ile birlikte artar. Ancak, bunun tamamen olasılıksal bir süreç olduğunu unutmayın! Yani, hangi sonuç kümesini elde edeceğimizi kesin olarak tahmin etmek mümkün değildir. Sadece istenen sonucu bulma olasılığını hesaplamak mümkündür:

• Pk - yinelemenin belirtilen gereksinimlere sahip çalışan bir varyant üretme olasılığı (bu olasılık gereksinimlere bağlı olarak büyük ölçüde değişebilir)
  
• C(n, m) - kombinasyon işlemi
  
• Pa = Sum(m0...m...n)[C(n, m)*Pow(Pk, m)*Pow(1-Pk, n-m)] - n yinelemeden sonra gereksinimlerimizi karşılayan en az m0 birincil varyanta sahip olma olasılığımız
• m0 - tatmin edici prototiplerin minimum sayısı
• Pa - "n" yinelemeden en az "m0" veya daha fazlasını elde etme olasılığı
• n - çalışan prototipleri aramak için mevcut maksimum döngü sayısı (sonuçları ne kadar süre beklemeye hazır olduğumuz)

Döngü sayısı zaman cinsinden de ifade edilebilir: ilk sekmedeki sayaçtan brute force hızını ve mevcut verileri işlemek için harcamaya hazır olduğunuz süreyi alın:

• Sh - saat başına yineleme sayısı olarak hız
• T - beklemeye hazır olduğumuz saat cinsinden zaman
• n = Sh*T

Benzer şekilde, belirli kalite gerekliliklerine uygun varyantlar bulma olasılığını hesaplamak mümkündür. Yukarıdaki formüller, sonucun doğrusallığı için bir gereklilik olan "Deviation" filtresinin kapsamına giren varyantların bulunmasına olanak sağlar. Bu filtre etkinleştirilmezse, her yineleme başarılı olarak kabul edilecek ve her zaman varyantlar olacaktır. Bulunan varyantlar kalite puanına göre sıralanacaktır. İhtiyaç duyulan kaliteye bağlı olarak, "Ps" değeri modülü alınan kalite değerinin bir fonksiyonu olacaktır. İhtiyacımız olan kalite ne kadar yüksekse, bu fonksiyonun değeri de o kadar düşük olur:

• Ps - belirli ek kalite gereksinimlerine sahip bir sonuç bulma olasılığı
• q - gerekli kalite
• qMax - mevcut en yüksek kalite
• Ps = Ps(|q|) = K*Px(|q|), q <= qMax
• K = Pk - bu katsayı rastgele bir varyant elde etme olasılığını dikkate alır (kaliteye dayalı varyantlar bu varyantlar arasından seçilir)
• Ps ' (|q|) < 0
• Lim (q-->qMax)[Ps(|q|)] = 0

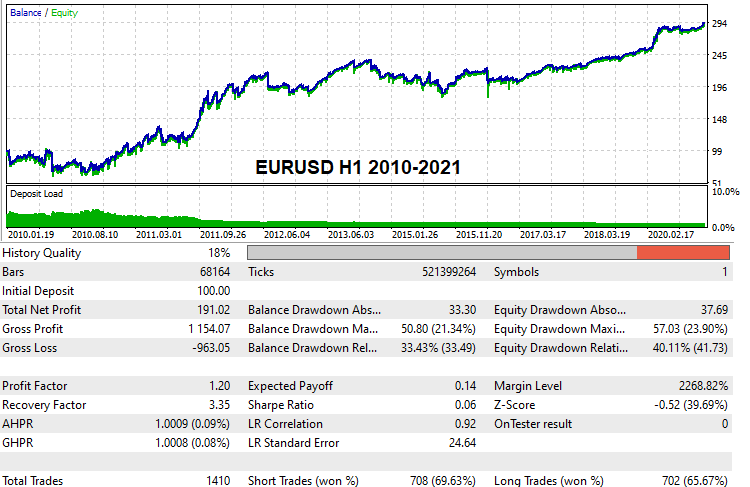
Bu fonksiyonun ilk türevi negatiftir ve gereksinimler arttıkça onları karşılama olasılığının sıfıra doğru eğilim gösterdiğini sembolize eder. "q" mevcut maksimum değere yöneldiğinde, bu bir olasılık olduğundan, bu fonksiyonun değeri "0"a yönelir. Eğer "q" maksimum değerden büyükse, seçilen algoritma daha yüksek bir kaliteye sahip olamayacağı için bu fonksiyon anlamsızdır. Bu fonksiyon, "q" rastgele değişkeninin olasılık yoğunluk fonksiyonundan kaynaklanır. Aşağıdaki şekil Ps(q) ve rastgele değişken P(q)'nun olasılık yoğunluğunun yanı sıra diğer önemli büyüklükleri göstermektedir:

Bu görüntülere dayanarak:

• Integral(q0, qMax)[P(q)] = Integral(-qMax, -q0)[P(q)] = K*Px(|q|) = Ps(|q|) - bu, q0 ile qMax arasında |q| olan bir varyantın mevcut yineleme sırasında bulunma olasılığıdır
• Integral(q1, q2)[P(q)] - yineleme sonucunda q1 ve q2 arasında bir kalite değerinin elde edilme olasılığı (bu, rastgele değişken dağılım fonksiyonunun nasıl yorumlanacağına dair bir örnektir)
  

Dolayısıyla, ne kadar çok kalite istersek, o kadar çok zaman harcamamız gerekecek ve o kadar az varyant bulunacaktır. Buna ek olarak, her yöntemin kalite değeri üzerinde bir üst sınırı vardır ve bu hem analiz ettiğimiz verilere hem de yöntemimizin mükemmelliğine bağlıdır.

İkinci sekmede optimizasyon

İkinci sekmedeki optimizasyon süreci birincil arama sürecinden biraz farklıdır. Yine de bir yineleme ve gereksinimlerimizi karşılayan bir varyant elde etme olasılığını kullanır. Bu sekmede çok daha fazla filtre vardır, buna bağlı olarak iyi sonuçlar elde etme olasılığı daha düşüktür. Bununla birlikte, ikinci sekme zaten işlenmiş varyantları geliştirdiğinden, ilk sekmede bulunan seçenekler ne kadar iyi olursa, ikincisinde de o kadar iyi sonuçlar elde edilecektir. Belirli bir varyantın geliştirildiği nihai formül Bernoulli denklemine biraz benzemektedir. İlgilendiğimiz şey, filtrelerimizin kapsamına giren en az bir varyant elde etme olasılığıdır. Bunu açıklayacağım:

• Py = Sum(1...m...n)[Sum(0...i...C(n, m)-1){Çarpım(0...j...i-1)[Pk[j])*Çarpım(i...j...m)[1-Pk[j]]}] - filtre gereksinimlerini karşılayan en az bir varyant elde etme olasılığı
  
• Pk[i] - ikinci sekmedeki filtrelerin gereksinimlerini karşılayan bir varyant elde etme olasılığı
  
• n - optimizasyon aralığını bölme (ikinci sekmedeki Interval Points değeri)

Optimizasyon, MetaTrader 4 ve MetaTrader 5 optimize edicileriyle tamamen aynı şekilde gerçekleştirilir, ancak yalnızca alış veya satış sinyali olan bir parametreyi optimize ederiz. Optimizasyon adımı, optimizasyon aralığını kaç parçaya böldüğümüze bağlı olarak otomatik olarak hesaplanır (Interval Points). Optimize edilen sayının en yüksek değeri, ilk sekmedeki arama işlemi sırasında hesaplanır. İlk sekmedeki işlem tamamlandıktan sonra, optimize edilen sayının değerlerindeki dalgalanma aralığını biliriz. Dolayısıyla, ikinci sekmede, bu aralığı bölmek için yalnızca grid hassasiyetini ayarlamamız gerekir. Varyant, daha iyi bir kalite elde edildiğinde güncellenecek olan ikinci sekmede bir yuvada yer alır. 

Yine, kalite gerekliliklerine sahip bazı varyantları elde etme olasılığı, yukarıdakine benzer bir dağılım fonksiyonuna sahip olacaktır. Bu, aynı formülleri küçük bir ayarlamayla kullanabileceğimiz anlamına gelir:

• Integral(q0, qMax)[P(q)] = Integral(-qMax, -q0)[P(q)] = K*Px(|q|) = Pz(|q|) - bu, mevcut yineleme sırasında q0 ile qMax arasında |q| olan bir varyantın bulunma olasılığıdır
• K = Py

Buradaki tek fark, yukarıda elde ettiğimiz yeni olasılığa eşit olan "K" katsayısıdır. Gerekli kalitede bir varyant elde etme olasılığı çok düşüktür, ancak ilk sekmede bu türden çok sayıda varyantımız vardı, bu nedenle ne kadar çok varyant elde edersek o kadar iyi olur. Ayrıca, ilk sekmede ne kadar çok varyant üretilirse, ikincisinde o kadar iyi varyantlar elde edilebilir. Hesaplama benzerdir. Ne yazık ki Bernoulli formülü burada uygulanamaz, ancak onun yerine daha önce ele alınan yapı kullanılabilir. Bu durumda, bir varyantın optimizasyonu ayrı bir yineleme olarak yorumlanır. Dolayısıyla yineleme sayısı tam olarak bu sayıya eşit olacaktır. Gereksinimlerimizi karşılayan en az bir varyanta ihtiyacımız vardır, bu nedenle önceki formül bize mükemmel bir şekilde uymaktadır. Burada Pk, Pz[j](|q|) fonksiyonları ailesi tarafından belirlenen Pz ile değiştirilir, çünkü her optimizasyon varyantı için ayrı bir fonksiyon vardır.

• Pb = Sum(1...m...n)[Sum(0...i...C(n, m)-1){Çarpım(0...j...i-1)[Pz[j])*Çarpım(i...j...m)[1-Pz[j]]}]
  
• n - ilk sekmede bulunan varyantların sayısı

Dolayısıyla, ne kadar uzun süre brute force uygularsanız, o kadar iyi kalite elde edersiniz. Ancak, her parametrenin olasılıkları ve sonucu etkilediğini unutmayın. Aşırı kaynak tüketimini önlemek adına makul ayarlar kullanın. Modern bilgisayarlar çok güçlüdür, ancak makul ayarların ve süreç ayrıntılarının bilinmesinin hesaplama verimliliğini birçok kat artırabileceğini unutmayın.

Geçmişe takılı kalmak ve aşırı uyum üzerine

Birçok otomatik ticaret sistemindeki sorun, aşırı eğitim almaları ve geçmişe uyum sağlamalarıdır. Ayda yüzde 1000'e varan etkileyici sonuçlar gösterecek bir sistem oluşturmak mümkündür. Ancak bu tür sistemler gerçekte çalışmaz.

Bir ticaret sistemi ne kadar çok girdi parametresine sahipse ve Uzman Danışman mantığının değişkenliği ne kadar büyükse, böyle bir Uzman Danışman geçmişe o kadar güçlü yapışır. Mesele şu ki, bir fiyatın başka bir veri formatına nasıl dönüştürüleceğine dair çok basit bir sürecimiz vardır. Her zaman hem ileri hem de geri veri dönüştürme işlemi sağlayabilen ileri ve geri dönüştürme işlevleri vardır. Bu, şifreleme ve şifre çözme ile karşılaştırılabilir. Örneğin, WinRar arşivi bir şifreleme örneğidir. Görevimiz bağlamında, şifreleme algoritması optimizasyon sürecinin ve ticaret mantığının varlığının bir kombinasyonudur. Optimize edicide yeterli sayıda geriye dönük test ve belirli bir esnek mantık bir mucize yaratabilir. Bu durumda, ticaret mantığı, geçmişteki değerlere dayanarak gelecekteki fiyatların kodunu çözen bir kod çözücü görevi görür.

Ne yazık ki, tüm Uzman Danışmanlar bir dereceye kadar geçmişe takılıdır. Bununla birlikte, gelecekte bir miktar işlevselliği koruması gereken mantıklı bir kısım da vardır. Böyle bir algoritmanın elde edilmesi son derece zordur. Belirli bir algoritmanın maksimum adil tahmin kapasitesini bilmiyoruz ve bu nedenle aşırı eğitim sınırlarını belirleyemiyoruz. Öyle bir algoritmaya ihtiyacımız var ki, bir sonraki mum hareketini mümkün olan en yüksek olasılıkla tahmin edebilsin. Burada, fiyat verisini sıkıştırma derecesi ne kadar güçlü olursa, algoritma o kadar güvenilir olur. Örneğin sin(w*t) fonksiyonunu ele alalım. Fonksiyonun sonsuz sayıda [X[i], Y[i]] noktasına karşılık geldiğini biliyoruz - bu, kısa bir sinüs fonksiyonuna sıkıştırılmış sonsuz uzunlukta bir veri dizisidir. Bu ideal bir veri sıkıştırmasıdır. Böyle bir sıkıştırma gerçekte mümkün değildir ve her zaman bir tür veri sıkıştırma oranına sahip oluruz. Bu katsayı ne kadar yüksek olursa, piyasa formülü tanımının kalitesi de o kadar yüksek olur.

Benim yöntemim sabit miktarda değişken veri kullanmaktadır. Bununla birlikte, diğer tüm yöntemlerde olduğu gibi, aşırı uyum olasıdır. Geçmiş aşırı eğitiminden kaçınmanın tek yolu sıkıştırma oranını artırmaktır. Bu sadece analiz edilen geçmiş bölümünün büyüklüğünü artırarak uygulanabilir. Ayrıca ikinci bir yol daha vardır - formüldeki analiz edilen çubukların sayısını (Bars To Equation) azaltmaktır. İlk yöntemi kullanmak daha iyidir, çünkü formüldeki çubuk sayısını azaltarak "qMax" üst sınırını artırmak yerine düşürürüz. Özetle, eğitim için en iyisi büyük örneklemler ve yeterli "Bars To Equation" kullanmaktır, ancak aynı zamanda bu değerdeki aşırı artışın brute force hızını azalttığı ve kaçınılmaz olarak daha yüksek bir oranın geçmişe aşırı uyum sağlama riskini yarattığı unutulmamalıdır.

Kullanım önerileri

Test sırasında, Awaiter.exe ana programını yapılandırmak için bazı önemli ince ayrıntılar belirledim. İşte bunlardan en önemlileri:

1. Tüm sekmelerde istediğiniz ayarları yaptıktan sonra, onları kaydettiğinizden emin olun (Save Settings düğmesi)
2. Spread Control ikinci sekmede etkinleştirilebilir
3. HistoryWriter Uzman Danışmanı aracılığıyla fiyat oluştururken mümkün olduğunca büyük bir örneklem kullanın (en az 10 yıllık geçmiş)
4. İlk sekmede daha fazla varyant kaydedilebilir, 1000 yeterli görünmektedir (Variants Memory)
5. Optimizasyon sekmesinde büyük bir Interval Points değeri ayarlamayın (20 - 100 yeterlidir)
6. Gerçek tikler üzerinde bir geriye dönük testi geçebilecek iyi ayarlar elde etmek istiyorsanız, varyantlarda çok sayıda emir gerektirmeyin (Min Orders)
7. Varyant arama hızını kontrol etmelisiniz (brute force uzun süredir çalışıyorsa ve hiçbir varyant bulunamıyorsa, muhtemelen ayarları değiştirmelisiniz)
8. Kararlı sonuçlar elde etmek için Deviation değerini "0.1 - 0.2" aralığında ayarlayın; 0.1 en iyi seçenektir
9. Optimizasyon sekmesinde FOURIER denklemini kullanırken, "Spread Control" seçeneğini etkinleştirin (formül makas gürültüsüne karşı son derece hassastır)

Sonuç

Lütfen bu çözümü kutsal bir kase olarak görmeyin. Bu sadece bir araçtır. MetaTrader 4 ve MetaTrader 5 terminallerinde ek programlama veya optimizasyon olmadan kullanılabilecek verimli ve kullanıcı dostu bir çözüm uygulamak zordur. Bu çözüm tam olarak bu şekildedir ve genel kullanıma hazırdır. Umarım bu yöntem sizin için faydalı olur. Tabii ki, hala iyileştirme için çok yer vardır, ancak genel olarak hem piyasa araştırması hem de ticaret için çalışan bir araçtır.

Proje hakkında bazı fikirlerim daha var, boş zamanım oldukça onları da yavaş yavaş gerçekleştirmeyi umuyorum. Bunlardan biri, en ünlü osilatör göstergelerine ve Bollinger Bands veya Moving Average gibi fiyat göstergelerine dayanan mantıksal bir polinomun oluşturulmasıdır. Ancak bu konsept biraz daha karmaşıktır. "Gösterge çaprazlamasında ticaret yapmak" yerine daha faydalı fikirler uygulamak istiyorum. Ayrıca makalenin okuyucular için yeni şeyler ve bazı genel faydalı bilgiler sağlamasını umuyorum.

Serinin önceki makalelerine linkler

• Model aramada brute force yaklaşımı (Bölüm III): Yeni ufuklar
  
• Model aramada brute force yaklaşımı (Bölüm II): Yoğunlaşma
  
• Model aramada brute force yaklaşımı