Otomatik ticaret için faydalı ve ilginç teknikler

Giriş

Yazarların veya yatırımcıların kârlı olması gerektiğini düşündüğü birçok ticaret tekniği vardır. Bu makalede bu teknikleri ele almayacağım, çünkü çok çeşitli kaynaklarda bunlar hakkında çok fazla bilgi vardır. Bu yöntemlerle ilgili yeni ya da ilginç bir şey söyleyemem. Bunun yerine, bu makaleyi hem teorik hem de pratik olarak faydalı olabilecek birkaç yararlı ve standart dışı tekniğin bir koleksiyonu olarak oluşturmaya karar verdim. Bu tekniklerden bazıları size tanıdık gelebilir. En ilginç yöntemleri ele almaya çalışacağım ve neden kullanmaya değer olduklarını açıklayacağım. Ayrıca, bu tekniklerin pratikte ne şekilde kullanılabileceklerini göstereceğim.

Son çubuk hareketini kullanan kısmi pozisyon kapatma algoritması

Teori:

Bu yaklaşım, bir pozisyon açtığımızda ve fiyatın hangi yönde daha fazla hareket edeceğinden emin olmadığımızda yararlı bir ticaret tekniği olarak hizmet edebilir. Akıllı kısmi pozisyon kapatma, makastan kaynaklanan kayıpları telafi edebilir ve hatta iyi bir optimizasyonun ardından kâr sağlayabilir.

Nereden çıkacağımızı bilmediğimizi, ancak halihazırda bir pozisyona girmiş olduğumuzu varsayalım. Hangi yöne girdiğimiz önemli değildir. Her halükarda, bir noktada pozisyonu kapatmak zorunda kalacağız. Elbette bazı yatırımcılar pozisyonlarını yıllarca koruyabilir. Ancak, robotun yoğun bir şekilde ticaret yapması ve yüksek bir işlem sıklığı sağlaması gerektiğini varsayıyoruz. Tüm hacimden bir anda veya pozisyonu kısmen kapatarak birkaç adımda çıkmak mümkündür. Piyasanın yatay bir yapıya sahip olduğunu biliyoruz, bu da fiyatın mevcut yarım dalganın başlangıcındaki konuma geri dönme eğiliminde olacağını ifade eder. Başka bir deyişle, yukarı yönlü bir hareket, devam etme olasılığının her zaman %50'den az olduğu anlamına gelir. Dolayısıyla, ters yönde bir hareket olasılığı da %50'den fazladır. Tüm pozisyonu kapatırsak, tüm dalgaları ve kârı kaçırabiliriz, çünkü dalgaların gelecekteki genliğini bilmiyoruz. Kısmi kapatma burada yardımcı olabilir. Gelecekteki dalgaların doğasını bilmediğimiz gerçeğine dayanarak maksimum kârı elde edebileceğiz.

Artık dalgaların ne olduğunu ve piyasadan asla kaybolmayacaklarını bildiğimize göre, giriş yanlış yapılsa bile en azından bir miktar kâr elde edilmesini sağlayacak olan pozisyon kapatma prensibiyle başlayabiliriz. Böyle bir mekanizma aslında mevcuttur.

Bu tür birçok algoritma olabilir, ancak ben sadece en verimli olduğuna inandığım bir tanesini göstereceğim. Bir önceki tam oluşmuş mumdaki hareket ne kadar büyük ve güçlüyse, oldukça güçlü bir geri çekilme hareketinin olma olasılığının o kadar yüksek olduğu varsayımından yararlanır. Genel olarak konuşursak, bu mekanizmanın amacı nedir? Çok basittir. Amaç, zararı azaltırken kârı artırmaktır. Güçlü hareketler (impulse’lar) de aslında dalgalardır. Ancak bu dalgalar normal klasik dalgalardan çok daha kullanışlıdır. Mesele şu ki, piyasaya en yakın olan dalgalar daha güvenilirdir. Güçlü hareket ne kadar güçlü ve meydana gelme süresi ne kadar kısa olursa, yakın gelecekte bir geri çekilme olasılığı ve beklenen geri çekilmenin büyüklüğü de o kadar yüksek olur. Buradaki fikir, mekanizmayı, güçlü hareketin gücü arttığında kısmi pozisyon kapatmanın da daha güçlü olacak şekilde düzenlemektir. Bunu bir şekil üzerinde göstereceğim:

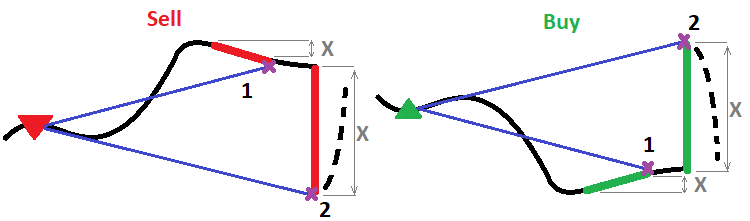
Pozisyonun kapatılacak kısmının hacmini hesaplamak için herhangi bir fonksiyon kullanılabilir. İki tanesini göstereceğim. Biri doğrusal, diğeri ise kuvvettir:

• {D} - kuvvet
• {X} - önceki çubuğun puan cinsinden hareketi
• {C} - ölçek katsayısı
• {Lc(X) = C*Pow(X, D)} - mevcut mumda kapatılacak lotu hesaplayan kuvvet fonksiyonu
• {Lc(X) = C*X} - mevcut mumda kapatılacak lotu hesaplayan doğrusal fonksiyon

Yakından bakarsanız, doğrusal fonksiyon D = 1 için kuvvet fonksiyonunun özel bir durumudur, bu yüzden sadece düşünme mantığının başlangıcına bir örnek olduğu için onu atlayabiliriz. Düşünmek ilk başta her zaman basittir, ancak üzerinde yeterli süre düşündükten sonra çok daha çok yönlü araçlar elde ederiz. Yalnızca basit bir şeyle başlamak gerekir.

Bu katsayıları doğrudan belirleme ve ardından etkilerini önemseme ihtiyacından kaçınmak için, bu katsayıları belirleyecek birkaç kontrol parametresi sunacağız:

• {StartLotsToOnePoint} - X = 1 olduğunda pozisyon bu değer kadar kapatılır (girdi parametresi)
• {PointsForEndLots} - son pozisyon kapanış hızı için bir önceki mumun kâr yönüne doğru hareketi (girdi parametresi)
• {EndLotsToOnePoint} - X = PointsForEndLots olduğunda pozisyon bu değer kadar kapatılır (girdi parametresi)

Şimdi katsayıları hesaplamak ve fonksiyonun girdi parametreleriyle ifade edilen son halini elde etmek için bir denklem sistemi oluşturalım. Bu amaçla, düşünceler matematiksel ifadelere dönüştürülmelidir:

1. {Lc(1) = StartLotsToOnePoint}
2. {Lc(PointsForEndLots) = EndLotsToOnePoint}
   

Tüm denklemlerimiz hazır. Şimdi onları genişletilmiş biçimde yazacağız ve kademeli olarak dönüştürerek çözmeye başlayacağız:

1. {C*Pow(1, D) = StartLotsToOnePoint}
2. {C*Pow(PointsForEndLots, D ) = EndLotsToOnePoint}
   

İlk denklemde, herhangi bir derecedeki 1'in kendisine eşit olduğu göz önüne alındığında, C'yi hemen bulabiliriz:

• {C = StartLotsToOnePoint}

İkinci denklemin her iki tarafını "C"ye böldüğümüzde ve ardından denklemin her iki tarafının "PointsForEndLots" tabanına göre logaritmasını hesapladığımızda aşağıdaki sonucu elde ederiz:

• {log(PointsForEndLots)[Pow(PointsForEndLots, D)] = log(PointsForEndLots)[EndLotsToOnePoint/C]}

Tabanı içeriğine eşit olan, herhangi bir kuvvete yükseltilmiş logaritmanın ilgili kuvvete eşit olduğunu düşünürsek, denklemi istenen kuvvete göre çözebiliriz:

• {D =  log(PointsForEndLots)[EndLotsToOnePoint/C]}

İkinci bilinmeyen katsayıyı bulduk. Ancak hepsi bu kadar değildir, çünkü MQL4 ve MQL5'te ihtiyacımız olan herhangi bir tabanda logaritma uygulayan temel bir fonksiyon yoktur, yalnızca doğal algoritma bulunmaktadır. Dolayısıyla, logaritmamızın tabanını doğal logaritma ile değiştirmemiz gerekir (doğal algoritma, tabanı Euler sayısı olan logaritmadır). Herhangi bir logaritma doğal logaritma cinsinden ifade edilebildiğinden, dilde başka logaritmaların olmaması bir sorun teşkil etmez. Bu, matematikten en azından bir şeyler anlayan herkes için oldukça kolay olacaktır. Tabanı değiştirdikten sonra, istediğimiz katsayı için formül aşağıdaki gibi görünecektir:

• {D = ln(EndLotsToOnePoint/C)/ln(PointsForEndLots)}

Halihazırda bilinen C katsayısını yerine koyalım, böylece şunu elde ederiz:

• {D = ln(EndLotsToOnePoint/StartLotsToOnePoint)/ln(PointsForEndLots)}

Şimdi her iki katsayıyı da fonksiyonumuzun şablonuna yerleştirebilir ve nihai formunu elde edebiliriz:

• {Lc(X) = StartLotsToOnePoint*Pow(X, ln(EndLotsToOnePoint/StartLotsToOnePoint)/ln(PointsForEndLots))}
  

Bu fonksiyonun avantajı, derecenin bire eşit, birden büyük veya birden küçük olabilmesidir. Böylece, herhangi bir piyasa ve ticaret enstrümanına uyum sağlamada maksimum esneklik sağlar. D = 1 ise, doğrusal fonksiyon elde ederiz. D > 1 ise, fonksiyon tüm dalgaların ölçeklenebilir olduğu ve belirli bir genlikteki dalga sayısının genlikle ters orantılı olduğu varsayımına göre ayarlanır (yani, aynı zaman aralığında örneğin M5 ve H1'deki dalga sayısını sayarsak, H1'de 12 kat daha az dalga olduğu ortaya çıkacaktır, çünkü saatlik mum sayısı beş dakikalık mum sayısından 12 kat daha azdır). D < 1 ise, küçük dalgalardan daha fazla yüksek genlikli dalga olmasını bekleriz. D > 1 durumunda da çoğunlukla düşük genlikli dalgalar olduğunu varsayarız. 

Ayrıca, çubuklar şeklinde ayrıştırılmış bir fiyat serisi kullanmak zorunda olmadığınızı da unutmayın - tikler ve uygun gördüğünüz diğer fiyat segmentlerini kullanabilirsiniz. Halihazırda çubuklarımız olduğu için burada çubukları kullanıyoruz.

Kod:

Kodda bu fonksiyon şu şekilde görünecektir:

double CalcCloseLots(double orderlots0,double X)
   {
   double functionvalue;
   double correctedlots;
   if ( X < 0.0 ) return 0.0;
   functionvalue=StartLotsToOnePoint*MathPow(X ,MathLog(EndLotsToOnePoint/StartLotsToOnePoint)/MathLog(PointsForEndLots));
   correctedlots=GetLotAniError(functionvalue);
   if ( correctedlots > orderlots0 ) return orderlots0;
   else return correctedlots;
   }

Lotları yalnızca doğru değeri alacak şekilde düzelten fonksiyon mor renkle vurgulanmıştır (içerisini göstermenin bir anlamı yoktur). Fonksiyonun kendisi yeşil renkle vurgulanan operatör altında hesaplanır, ancak burada çağıracağımız daha genel bir fonksiyonun bir parçasıdır:

void PartialCloseType()// close order partially
   {
   bool ord;
   double ValidLot;
   MqlTick TickS;
   SymbolInfoTick(_Symbol,TickS);
            
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == _Symbol )
         {
         if ( OrderType() == OP_BUY )
            {
            ValidLot=CalcCloseLots(OrderLots(),(Open[0]-Open[1])/_Point);
            if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.bid,MathAbs(SlippageMaxClose),Green);
            }
         if ( OrderType() == OP_SELL )
            {
            ValidLot=CalcCloseLots(OrderLots(),(Open[1]-Open[0])/_Point);
            if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.ask,MathAbs(SlippageMaxClose),Red);
            }         
         break;
         }
      }

MT4Orders kütüphanesini kullandığımız için bu kod MQL5'te de derlenebilir. Lütfen bu fonksiyonların sadece test için uygun olduğunu unutmayın. Gerçek ticaret için kullanmak amacıyla, onları hatalar ve hesaplanmamış durumlar açısından dikkatlice incelemeli ve iyileştirmelisiniz. Mevcut sürüm, strateji sınayıcıda test etmek için oldukça uygun durumdadır.

Uzman Danışmanı test etme:

Nasıl çalıştığını göstermek adına MetaTrader 4 için bir Uzman Danışman sürümü oluşturdum, çünkü MetaTrader 5'te test ederken, makas muhtemelen görmek istediğimiz her şeyi gizleyecektir. Bunun yerine, makası 1 olarak ayarladım ve rastgele bir yönde pozisyon açmayı seçtim:

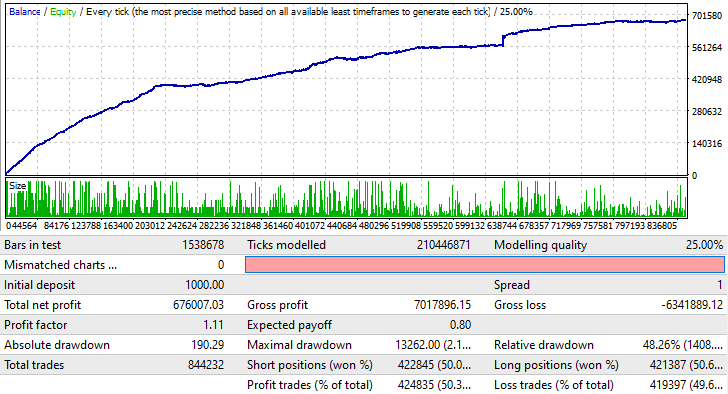
Bu aynı zamanda diğer döviz çiftlerinde de aynı şekilde çalışır. Daha yüksek zaman dilimlerinde de çalışabilir, ancak bu, uygun ayarları bulmak için biraz sabır gerektirir. Ancak bu test, bu Uzman Danışmanı hemen bir gerçek hesapta başlatabileceğiniz anlamına gelmez. Bu sadece, bu tekniğin doğru kullanıldığında faydalı olabileceğinin bir kanıtıdır. Bu noktada bu Uzman Danışman bile kâr açısından çok ama çok yetersizdir. Ancak iyi bir sinyal ve uygun bir yaklaşımla birleştirildiğinde, bu yöntem kârlı olabilir.

Hibrit lot varyasyonu algoritması

Piyasa araştırmasının en başından beri, herhangi bir sistemin kâr faktörünü pozitif değerlere doğru nasıl kaydırabileceğimi merak ediyordum. Bu, makasa çok fazla bağlı olmayan herhangi bir stratejinin, kâr faktörü bire yakın olan diğer stratejilere kıyasla çok büyük bir avantaj elde edeceği anlamına gelir. Kâr faktörünün tam olarak neden iyileştirilmesi gerekiyor? Cevap çok basittir: çünkü hem tüm sistemin göreceli düşüşü hem de sistemin kârlılığı bu değişkene bağlıdır. Böyle bir teknik vardır ve bunu size göstereceğim. Ama önce, lot manipülasyonunu kullanabilen en ünlü ticaret tekniklerini hızlıca gözden geçirelim. Kâr faktörünü arttırmak için aşağıdaki teknikler bulunmaktadır:

• Martingale
• Ters martingale

Aslında her şey, sıklıkla tartışılan ancak hayal kırıklığından başka bir şey getirmeyen iki yönteme dayanmaktadır. Her şey, Grid ve martingale: bunlar nedir ve nasıl kullanılır? makalesinde açıkladığım çok basit bir matematiksel prensiple ilgilidir. Prensiplerin kendilerini değil, hepsinde ortak olan şeyi tanımlamaktadır. Ortak olan şey, bazı koşullara bağlı olarak lotun azaltılması ya da artırılmasıdır. Koşulların fiyat oluşumunun doğasıyla hiçbir ilgisi yoksa, böyle bir sistem açıkça kârsız olur.

Lot varyasyonu kullanan her strateji temel bir sinyale sahiptir. Tüm emirler için lotun aynı olmasını sağlayarak bunu elde edebiliriz. Bu, sinyalin herhangi bir şekilde fiyat oluşumunun doğasıyla ilgili olup olmadığını anlamamıza yardımcı olacaktır. Çoğu durumda, böyle bir sinyal sıfır matematiksel beklenti üretecektir. Ancak bu sinyalde aynı anda hem ileri hem de ters martingale kullanmamıza izin verebilecek bir parametre vardır. Gerekli koşul, çok sayıda düşük genlikli dalganın varlığıdır. Martingale ve ters martingale’i birlikte doğru bir şekilde kullanırsanız, onları sıfır matematiksel beklentiyi pozitif bir beklentiye dönüştürecek bir tür hibrit bir mekanizmaya dönüştürebilirsiniz. Aşağıdaki görüntü bunun nasıl görünebileceğini göstermektedir:

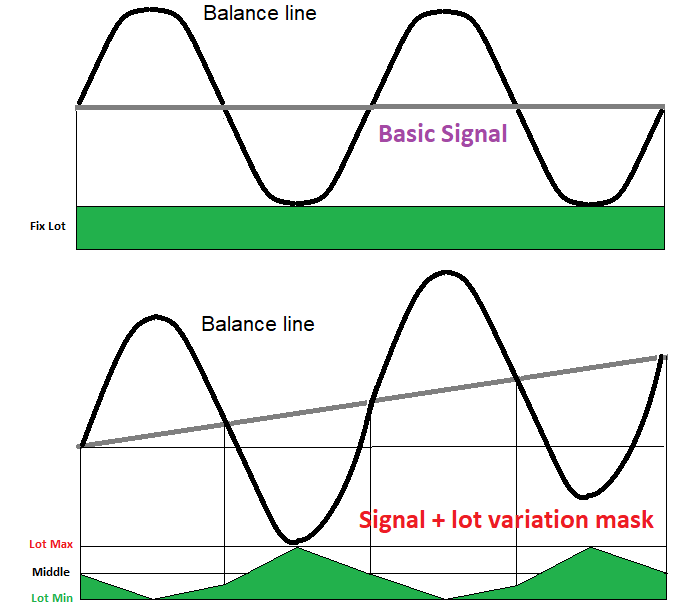
Teori:

Burada, makas ve komisyonu hesaba katmadan, bir gün başlangıç bakiyesine göre pozitif veya negatif bir kârla ticareti durdurmaya karar verene kadar veya sistem makaslar, komisyonlar ve swaplardan kaynaklı olarak bakiyenizi yavaşça tüketene kadar her zaman başlangıç bakiyesi seviyesinin yakınında dolaşacak olan belirli bir bakiye çizgisine sahip olacağımızı varsayıyoruz. Bu, bakiye çizgisinin başlangıç bakiyesi etrafında dalgalanan dalgalı bir süreç olduğu anlamına gelir.

Buna dayanarak, tüm bakiye çizgisini yükselen ve düşen bölümlere ayırabiliriz (şekilde bir tam dalganın dörtte biri gösterilmektedir). Dalga çeyreği yükseliyorsa, lotlar azaltılmalıdır (ters martingale); dalga düşüyorsa, lotlar artırılmalıdır (martingale). Sonsuz lot artışının önündeki tek engel, herhangi bir hesabın izin verilen maksimum pozisyon hacmine sahip olmasıdır. Dolayısıyla, böyle bir durum mümkün olsa bile, bakiye ekstra pozisyon açmamıza izin vermeyecektir. Bu bağlamda, lot belirli bir değer koridorunda dalgalanmalı ve onun ötesine geçmemelidir. Bu nedenle önemli olan nokta, dalgaların genliğinin çok büyük olmaması, tercihen daha fazla küçük dalga ve daha az büyük dalga olmasıdır. Şekle ve aşağıdaki lot varyasyonu maskesine yakından bakarsanız, hibrit varyasyonu kullanarak, dalgalanmaların meydana geldiği çizginin nasıl yukarı doğru bir eğim kazanabileceğini anlayacaksınız, bu da pozitif bir matematiksel beklenti ve kâr faktörüne eşdeğerdir.

Bu durumda lotlar nasıl hesaplanır? Durum ilk bakışta belirsiz görünebilir. Açıkçası, lot kanalımızın sınırlarından birine ulaşabilir ve asla dışarı çıkmayabilir. Böyle bir durumda, ortalama lot değeri etrafında istikrarlı dalgalanmalar elde etmek adına başlangıç lotuna geri dönmek için bir mekanizma sağlamalıyız. Böyle bir sistemin bariz ve tek dezavantajı, büyük genlikli dalgalara karşı toleranssız olmasıdır. Düşük genlikli bir harekette mekanizma mükemmel performans gösterecektir. Bu sorun, bir sonraki lotu, fonksiyonun kendisi lotları ortaya doğru itecek şekilde hesaplayan bir fonksiyonla çözülür ve önceki kapalı emrin lotu sınırlardan birine ne kadar yakınsa, itme o kadar güçlü olur. Bunu aşağıdaki şekilde göstereceğim:

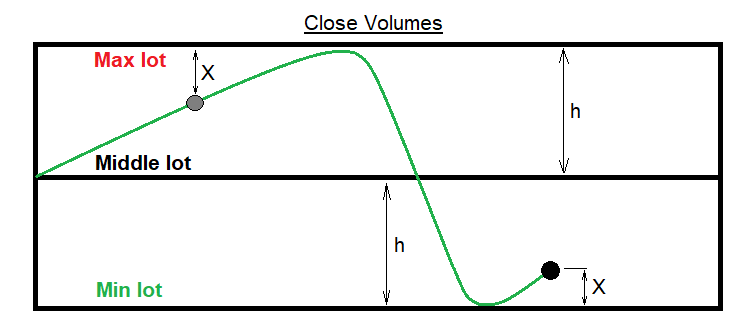
Şimdi şekildeki gösterimi kullanarak bu görev için uygun olan bir fonksiyonun genel bir formunu yazacağım. Ama önce, girdi parametrelerini ve yardımcı değişkenleri tanımlayalım:

Hibrit lot varyasyonunu kontrol etmek için girdi değişkenleri

• {MaxLot} - koridorun maksimum lotu (girdi parametresi)
• {MinLot} - koridorun minimum lotu (girdi parametresi)
• {LotForMultiplier} - hacmi artırmak veya azaltmak için referans lot
• {ProfitForMultiplier} - referans lot artışı veya azalışı için puan cinsinden zarar ve kâr

Yardımcı değişkenler

• {MiddleLot = (MaxLot+MinLot)/2} - maksimum ve minimum lot arasındaki orta lot
• {h = (MaxLot-MinLot)/2} - kanalın yarısının genişliği (hesaplamalar için gereklidir)
• {L} - geçmişteki son işlemin lotu
• {X} - yardımcı değişken
• {OrderProfit, OrderComission, OrderSwap, OrderLots} - komisyonsuz kâr, komisyon, swap ve geçmişteki son emrin kapanış hacmi (bunlar bilinmektedir)
• {TickSize} - hacminin 1 lota eşit olması ve fiyatın istenen yönde 1 puan hareket etmesi koşuluyla açık pozisyonun kârındaki artış
• {PointsProfit = (OrderProfit+OrderComission+OrderSwap)/(OrderLots*TickSize)} - puan cinsinden geçmişteki son emrin kârı

Lotların merkez çizgisinin üstünde veya altında olduğu durumlar için fonksiyon

• {L >= MiddleLot ? X = MaxLot-L} - eğer lotlar koridorun üst kısmındaysa, "X" değeri kanalın üst sınırına olan mesafedir
• {L < MiddleLot ?  X = L-MinLot} - eğer lotlar koridorun alt kısmındaysa, "X" değeri kanalın alt sınırına olan mesafedir
• {L >= MiddleLot & PointsProfit < 0 ? Lo(X) = OrderLots-LotForMultiplier*(PointsProfit/ProfitForMultiplier)*(X/h)} - kanalın üst sınırına yaklaşırken yavaşlayan lot artışı
• {L < MiddleLot & PointsProfit >= 0 ?  Lo(X) = OrderLots-LotForMultiplier*(PointsProfit/ProfitForMultiplier)*(X/h)} - kanalın alt sınırına yaklaşırken yavaşlayan lot düşüşü
• {L >= MiddleLot & PointsProfit >= 0 ?  Lo(X) = OrderLots-LotForMultiplier*(PointsProfit/ProfitForMultiplier)/(X/h)} - hızlandırılmış lot düşüşü 
• {L < MiddleLot & PointsProfit < 0 ?  Lo(X) = OrderLots-LotForMultiplier*(PointsProfit/ProfitForMultiplier)/(X/h)} - hızlandırılmış lot artışı

Okunması zor olduğu için tüm bu ilişkileri algılamak oldukça zordur. Her şeyi sürekli bir fonksiyonda birleştirmeye çalışırsanız, o kadar karmaşık bir yapı elde edersiniz ki, onunla çalışmak imkansız olur. Kodda nasıl göründüğünü daha sonra göstereceğim, böylece her şey daha net hale gelecektir. Burada MQL4 tarzı kod uygulamasını gösteriyorum. Kullanışlı ve popüler MT4Orders kütüphanesini kullanırsanız kod MQL5'te de kolayca çalıştırılabilir:

Kod:

double CalcMultiplierLot()
   {
   bool ord;
   double templot=(MaxLot+MinLot)/2.0;
   for ( int i=OrdersHistoryTotal()-1; i>=0; i-- )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_HISTORY );
      if ( ord && OrderSymbol() == CurrentSymbol &&  OrderMagicNumber() == MagicF )
         {
         double PointsProfit=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*MarketInfo(CurrentSymbol,MODE_TICKVALUE));
         if ( OrderLots() >= (MaxLot+MinLot)/2.0 )
            {
            if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0));
            if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0)) ;
            if ( PointsProfit == 0.0 ) templot=OrderLots();
            break;
            }
         else
            {
            if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((OrderLots()-MinLot)/((MaxLot-MinLot)/2.0));
            if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((Orderlots()-MinLot)/((MaxLot-MinLot)/2.0));
            if ( PointsProfit == 0.0 ) templot=OrderLots();
            break;
            }
         }
      }
   if ( templot <= MinLot ) templot=(MaxLot+MinLot)/2.0;
   if ( templot >= MaxLot ) templot=(MaxLot+MinLot)/2.0;
         
   return templot;
   }

Bu kütüphane özellikle her bir açık emri kontrol etmeniz gereken durumlarda faydalı olacaktır. Bu aslında bu yaklaşımın tüm mantığıdır. Algoritmanın girdi değişkenleri sarı renkle vurgulanmıştır.

Uzman Danışmanı test etme:

Bu Uzman Danışman, önceki Uzman Danışman ile aynı nedenle MetaTrader 4 için de tasarlanmıştır, çünkü kâr faktöründe bir iyileşme görmek daha kolay olacaktır:

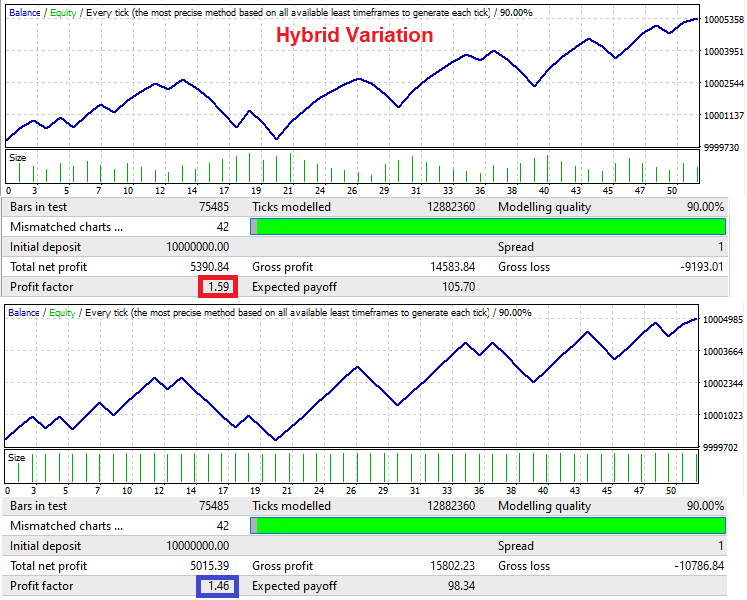
Bu Uzman Danışmandaki sinyaller sırayla oluşturulur. Alışı satış takip eder ve satışı da alış takip eder. Bu, mekanizmanın özünü göstermek için yapılır. İkinci testte sabit bir lot kullanılırken, ilk test için hibrit lot varyasyonu kullanılmıştır. Sistem, yalnızca orijinal sinyalde minimum bakiye dalgalanmaları olması durumunda kâr faktöründe bir iyileşme sağlayabilir. Sistem büyük dalgalara dayanamayacaktır.

Ortalama alma prensibi

Ortalama alma prensibi oldukça ilginç bir algoritmadır. Martingale ve piramitleme gibi kârsız olmasına rağmen, dalga ticaretinde yardımcı olabilecek çok ilginç bir özelliği vardır. Hareketin belirli bir seviyeye kadar devam edeceği ve daha sonra mutlaka belirli sayıda puan geri çekilme olacağı biliniyorsa, bu durumda martingale ile ortalama alma uygulanabilir. Bu teknik özellikle martingale ile iyi çalışır, çünkü martingale kâr faktörünü 1.0'dan büyük tutarken gerekli geri çekilmeyi azaltmanıza izin verir.

Bu prensip, fiyatın açık pozisyonumuz yönünde hareket etmemesi durumunda, bir süre sonra şüphesiz bu hareketin bir kısmı kadar geri çekileceği varsayımından yararlanır. Ama bu gerçekte her zaman gerçekleşmez, ancak dalgalarının doğasını inceleyerek birçok sembol için bu algoritmaya ince ayar yapabilirsiniz. Bu geri çekilmeden kâr elde edebilmek için onu tahmin etmemiz ya da deneysel olarak belirlememiz gerekir.

Bu aynı zamanda güçlü seviyelerde de işe yarar, çünkü çoğu zaman bir seviye aşıldığında piyasa terse dönüş için seviyeyi test etmeye çalışabilir. İlk işlemin yönünü doğru tahmin ettiysek ve kâr gerekli değere ulaştıysa, işlemi kapatır ve daha cazip görünen yönde yeni bir işlem açarız. Fiyat yanlış yöne gittiyse, belirli adımlarla pozisyonumuzun hacmini artırmayı deneyebiliriz. Pozisyonu artırırken çok dikkatli olmalıyız - beklenen geri çekilmeye bağlı olarak hassas bir şekilde yapılmalıdır. Aşağıda iki olası örnek verilmiştir.

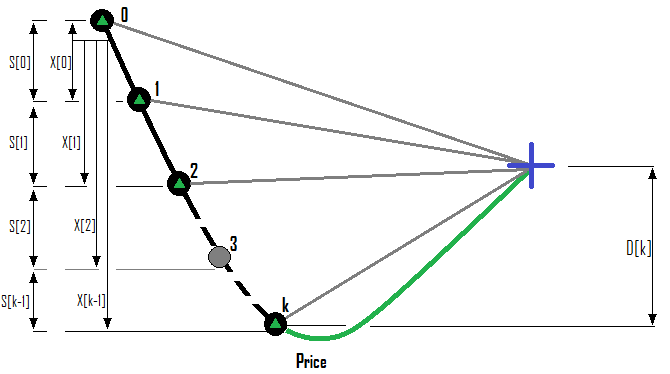
Bir Alış emri serisi için örnek:

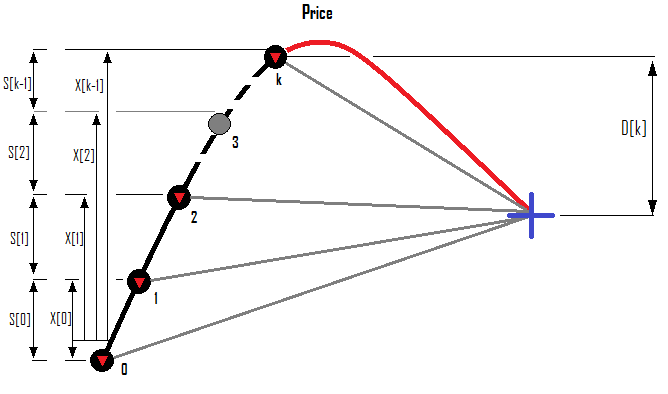
Bir Satış emri serisi için örnek:

Şimdi tüm emirlerin kâr veya zararının nasıl hesaplandığını ve mevcut duruma göre, gerekli geri çekilmeye dayalı olarak bir sonraki emrin lotunun nasıl hesaplanacağını göstereceğim. Bir pozisyon yelpazesini kapatmak için, bu yelpazenin neden inşa edilmesi gerektiğini ve hangi koşulun onu yararlı kıldığını bilmek gerekir. Ben olsam Kâr Faktörünü kullanırdım. Yelpaze pozitifse, kâr faktörü de pozitiftir. Tüm emirlerin toplam kârı pozitif olur olmaz yelpazeyi kapatmak aptalca olacaktır, çünkü sunucudaki herhangi bir fiyat dalgalanması veya bir kayma kârı negatif yöne taşıyabilir - bu tür yelpazeler bu koşullar altında işe yaramaz görünebilir. Buna ek olarak, döngünün kâr faktörü, otomatik bir stratejiyi optimize ederken veya ayarları manuel olarak ararken kullanılabilecek ortalama alma agresifliğinin ek olarak ayarlanması için bir olanak sağlar.

Bir serideki maksimum emir sayısında bir sınır olduğunu varsayalım. Ardından, k adet emir açtığımız bilinmeyen bir durumda olduğumuzu düşünelim - indeksleri herhangi bir koleksiyon veya dizide olduğu gibi 0'dan başlar. Dolayısıyla, serideki son emrin indeksi "k-1" olacaktır. Bir sonraki emri açtığımızda, endeksi k olacak ve emir sayısı ise "k + 1" olacaktır. Çıkarımlarımızı problemin girdi verilerine göre biçimlendirelim:

• {MaxOrders} - bir seride izin verilen maksimum emir sayısı
• {k = 0 ... 1 ... 2 ...  (MaxOrders-1)} - önceki öngörüden kâr elde edemezsek açmak istediğimiz serideki bir sonraki emrin endeksi
• {ProfitFactorMax} - kapanış için izin verilen kâr faktörü
• {i = 1 ... 1 ... 2 ... k} - yelpazenin mevcut emirlerinin ve açmak istediğimiz bir sonraki emrin indeksleri
• {S[i-1]} - bir önceki emirden mevcut emre olan puan cinsinden mesafe
• {X[i-1]} - serinin sıfırıncı emrinden mevcut emrine kadar olan puan cinsinden mesafe
• {D[k]} - serinin son emrinin açılış fiyatına göre istenen yönde tahmin edilen geri çekilme

Ek olarak, MQL4 ve MQL5 dillerinin, belirli bir emre atıfta bulunduğumuzda, tüm hesaplama seçeneklerini tanımlamak için ihtiyaç duyduğumuz aşağıdaki verileri sağladığını söyleyebiliriz:

• {P[i]} -komisyon ve swap hariç olmak üzere emrin kârı
• {С[i]} - seçilen emrin komisyonu
  
• {S[i]} - pozisyonu 0:00'da bir sonraki güne taşıma (rollover) sırasında emrin hesaplanan swapı
  
• {L[i]} - emrin hacmi
  
• {Sp[i]} - Alış/Satış pozisyonu açarken makas
• {TickSize} - hacminin 1 lota eşit olması ve fiyatın istenen yönde 1 puan hareket etmesi koşuluyla açık pozisyonun kârındaki artış

Bu değerlerin tümü otomatik ticarette pratik kullanım için gerekli olmayacaktır, ancak bu değerlerin hesaplanması için tüm olası seçeneklerin vurgulanmasına olanak tanırlar. Alakalı olan ve fiyatla ilişkili olarak gösterilebilecek bu değerlerden bazıları yukarıdaki şekillerde gösterilmiştir. Kodumda kullandığım en basit hesaplama yöntemiyle başlayalım:

İlk emir pozitif sonuçla kapanırsa, hiçbir şey yapmayız. Uygun gördüğümüz herhangi bir anda, istenen yönde yeni bir emir açarız. Fiyat hedefe ulaşmadıysa ve ters yönde gittiyse, bir sonraki emri açmak için fiyatın zarar oluşturan yönde kaç puan hareket etmesi gerektiğine karar vermeliyiz (S[k-1]). Fiyat bu seviyeye ulaştıysa, hangi geri çekilmenin uygun olduğuna karar vermeliyiz (D[k]). Devamında, şimdi açacağımız emrin lotunu belirlemeliyiz, böylece planlı bir geri çekilme ile, seçtiğimiz değerden (ProfitFactorMax) daha büyük tüm emirlerin gerekli kâr faktörünü elde ederiz. Bunu yapmak için, öncelikle halihazırda açık olan emirlerden hangi kârın elde edileceğini, hangi zararın oluşacağını ve bunların toplam değerini hesaplamamız gerekir. Bunun amacını daha sonra, ilgili formülleri yazdıktan sonra açıklayacağım:

Öncelikle, her bir spesifik emir için gelecekteki kâr değerini tanıtalım. Bu değer, gerekli geri çekilmenin gerçekleşmesi koşuluyla, mevcut kârdan ve emrin alacağı artıştan oluşur:

• {j = 0 ... 1 ... 2 ... k-1}
  
• {PF[j] = P[j]+С[j]+S[j]+(D[k]*L[j]*TickSize)} - gerekli geri çekilme gerçekleştiğinde emrin kârı bu değere eşit olacaktır
• {PF[k] = {(D[k]-Spread[k])*L[k]*TickSize} - bu değer, açmak istediğimiz pozisyonun gerekli lotunu içerdiğinden hesaplanamaz; ancak bu ifadeye daha sonra ihtiyaç duyulacaktır
  

İlk durumda P[i] değeri bilinmektedir ve bunu yerleşik dil fonksiyonlarını kullanarak elde edebileceğimiz gibi kendimiz de hesaplayabiliriz. Bu hesaplama yöntemi makalenin sonunda bir ek olarak gösterilecektir, çünkü her şey standart dil araçları kullanılarak bulunabilir. Serideki açacağımız son emre gelince, onun da bir komisyon ve swapa ihtiyacı vardır, ancak bu değerler yalnızca halihazırda açık olan emirler için elde edilebilir. Ayrıca, pozisyonun 0:00'dan geçip geçmeyeceğini bilmediğimiz için swap değerini belirlemek imkansızdır. Her zaman yanlış değerler olacaktır. Yalnızca pozitif swaplara sahip döviz çiftlerini seçebiliriz. 

Devamında, kârda ve zararda olan emirleri ayırmak ve ortaya çıkan kâr faktörünü hesaplamak için bu tahmin edilen kârı kullanabiliriz:

• {i = 0 ... 1 ... 2 ... k} - halihazırda açık olan emirlerin indeksleri
• {Pr[i] >= 0, Ls[i] >= 0} - işaretine bağlı olarak emrin kârını veya zararını kabul edecek 2 dizi ekleyelim (kâr ve zararın "+" işaretli olduğunu varsayacağız, bu, kâr faktörünü hesaplamak için yararlı olacaktır)
• {PF[i] < 0 ?  Pr[i] = 0 & Ls[i] = -PF[i]} - emrin kârı negatifse, kârı "0" olarak yazılır ve kâr değeri ters işaretle zarar değişkenine kaydedilir
• {PF[i] > 0 ? Ls[i] = 0 & Pr[i] = PF[i]} - emrin kârı pozitifse, uygun diziye yazılır ve zarar dizisine sıfır değeri ayarlanır
  

Bu dizileri doldurduktan sonra, toplam kâr ve zararı hesaplamak için formül yazabiliriz.

• {SummProfit = Summ[0, k](PF[i])} - tüm kârda olan emirlerin toplam kâr modülü
• {SummLoss = Summ[0, k](Ls[i])} - tüm zararda olan emirlerin toplam zarar modülü
  

Şimdi döngü kapanış koşulunu yazmamız gerekiyor:

• {SummLoss > 0 ? SummProfit/SummLoss = ProfitFactorMax}

Bu denklemi kullanabilmek adına, pozisyon yelpazesini kapatırken serideki son emrin kârının her zaman pozitif olduğunu anlamamız gerekir. Buna dayanarak şunu yazabilirsiniz:

• {SummProfit = Summ[0, k-1](PF[j])+PF[k]}
  

Bu değeri denklemde yerine koyarız ve aşağıdakileri elde ederiz:

• {(Summ[0, k-1](PF[j])+PF[k])/SummLoss = ProfitFactorMax}
  

Şimdi, bu denklemi PF[k] için çözerek şunu elde ederiz:

• {PF[k] = ProfitFactorMax*SummLoss-Summ[0, k-1](PF[j])}
  

PF[k] değeri için halihazırda bir formülümüz olduğundan, bu ifadeyi burada yerine koyabiliriz ve böylece şunu elde ederiz:

• {(D[k]-Spread[k])*L[k]*TickSize = ProfitFactorMax*SummLoss-Summ[0, k-1](PF[j])}
  

Şimdi bu denklemi L[k]'ya göre çözebiliriz. Böylece, son olarak, açılacak pozisyonun gerekli hacmini hesaplamak için formülü elde edeceğiz:

• {L[k] = (ProfitFactorMax*SummLoss-Summ[0, k-1](PF[j]))/((D[k]-Spread[k])*TickSize)}
  

Hepsi bu kadar. Şimdi yerleşik fonksiyonları kullanmadan P[i] değerini nasıl hesaplayacağımızı ele alalım.

• {P[i] = (X[i-1]-Spread[i])*L[i]*TickSize+С[j]+S[j]}
  

Geri çekilme değerinin hesaplanması

Şimdi geri çekilme değerinin hesaplanma yöntemlerine bakalım. Ben iki yol kullanıyorum. Çok sayıda yöntem olabilir, ancak ben sadece en faydalı olduğunu düşündüğüm iki yöntemi sunacağım. Geri çekilme, fiyatın ne kadar yanlış yöne gittiğine bağlı olarak hesaplanır. Bu, D[i] ve X[i]'nin tüm pozitif X ekseninde pozitif olan herhangi bir fonksiyonla ilişkilendirilebileceği anlamına gelir:

• {D = D(X)}
• {D[k] = D(X[k-1])}

Geri çekilmeyi hesaplamak için iki fonksiyon kullanıyorum. Birincisi doğrusaldır. İkincisi bir kuvvet fonksiyonudur. İkinci fonksiyon daha zor ama daha ilginçtir. İşte fonksiyonlar:

• {D = K*X}
• {D = DMin+C*Pow(S, X)}

Seçtiğimiz katsayılar renkli olarak vurgulanmıştır. Bu katsayılara bağlı olarak, fonksiyonlar farklı şekilde çalışmaya başlar ve buna göre stratejimizi belirli bir döviz çiftine veya zaman dilimine göre esnek bir şekilde ayarlayabiliriz.

1. {K} - doğrusal fonksiyon için geri çekilme katsayısı (otomatik bir sistem için girdi parametresi olarak da kullanılır) 
   
2. {DMin} - izin verilen minimum geri çekilme (D >= DMin, kuvvet fonksiyonu durumunda)
   
3. {C} - kuvvet fonksiyonunun ölçekleme katsayısı
4. {S} - üs alma işleminin tabanı

Açıkçası, dereceye C eklenebilir, ancak bu formda fonksiyonun daha okunabilir ve kullanımı kolay olduğunu düşünüyorum. Ayrıca K ve DMin değerlerinin girdi parametreleri olduğunu, dolayısıyla bu katsayıların bizim tarafımızdan zaten bilindiğini unutmayın. Kalan iki katsayının nasıl hesaplanacağı açık değildir. Şimdi bunu yapalım. 2 bilinmeyen değeri bulmak için en az iki denklemden oluşan bir sisteme ihtiyacımız vardır. Böyle bir sistemi yazabilmek için öncelikle fonksiyon formunun nasıl kontrol edileceğine karar vermemiz gerekir. Aslında, kuvvet fonksiyonunun mevcut formunu seçtim çünkü geri çekilmede yumuşak bir azaltma yapmak daha kolay ve daha uygun olacaktır. Bu yüzden kuvvet fonksiyonunu seçtim. Dikkate alınanlar aşağıdaki gibidir:

1. {HalfX} - ek geri çekilmenin yarısı için fiyat hareketi (fonksiyonu kontrol etmek için ek girdi parametresi)
2. {D(0) = DMin+K*DMin}
3. {D(HalfX) = DMin+K*DMin/2}

Böylece, çözeceğimiz gerekli denklem sistemini elde ederiz. Başka bir deyişle, fiyat hareketini ilk açık emre göre zarara doğru ayarlıyoruz, burada geri çekilme ilavesi başlangıçtaki değerin yarısıdır. Bu eklemenin başlangıçta maksimum bir değeri vardır. Sonuç olarak, minimum geri çekilmeden daha düşük bir değer alamayan bir fonksiyon elde ederiz ve X sonsuza yaklaştıkça, fonksiyon minimum geri çekilmeye ulaşır. Matematiksel olarak aşağıdaki şekilde ifade edilir:

• {D >= DMin}
  
• {Lim(X->+infinity) = DMin}

Şimdi bu denklem sistemini çözmeye başlayabiliriz, ancak önce tüm sistemi yeniden yazalım:

1. {DMin+C*Pow(S, 0) = DMin+K*DMin}
2. {DMin+C*Pow(S, HalfX) = DMin +K*DMin/2}

İlk denklemde, sıfır kuvvetindeki herhangi bir sayının bir olduğu gerçeğini göz önünde bulundurarak C'yi hemen bulabiliriz. Bu nedenle, S değişkenini hariç tutuyoruz. Şimdi tek yapmamız gereken denklemi C değişkenine göre çözmektir.

• {С = K*DMin}
  

Artık C'ye sahip olduğumuza göre, C değişkeni yerine basitçe önceki ifadeyi koyarak kalan bilinmeyen S'yi bulabiliriz:

• {Pow(S, HalfX) = 0.5}

Dereceyi ortadan kaldırmak için denklemin her iki kısmını da HalfX'in tersine yükseltmemiz gerekir. Sonuç olarak, aradığımız katsayı olacak aşağıdaki basit ifadeyi elde edeceğiz:

• {S = Pow(0.5, 1/HalfX)}

Şimdi katsayıları yerine koyarak kuvvet fonksiyonumuzu yazabiliriz. Böylece, bu stratejiyi uygulamak için ihtiyacımız olan her şeyi tanımlamış oluruz:

• {D(X) = DMin+K*DMin*Pow(Pow(0.5, 1/HalfX),X)}

Bu fonksiyon kodda bu şekilde görünecektir:

Kod:

double D(double D0,double K0,double H0,double X)
   {
   return D0+(D0*K0)*MathPow(MathPow(0.5,1.0/H0),X);
   }

İşte teoriyi test etmek için Uzman Danışmanda kullanılacak birkaç önemli fonksiyon daha. İlki, fiyattan serideki en yakın açık emre olan puan cinsinden mesafeyi belirleyen fonksiyondur:

double CalculateTranslation()
   {
   bool ord;
   bool bStartDirection;
   bool bFind;
   double ExtremumPrice=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL ) bStartDirection=false;
         if ( OrderType() == OP_BUY ) bStartDirection=true;
         ExtremumPrice=OrderOpenPrice();
         bFind=true;
         break;
         }
      }      
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                        
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         if ( OrderType() == OP_BUY && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         }
      }
   if ( bFind )
      {
      if ( bStartDirection ) return (ExtremumPrice-Close[0])/_Point;
      else return (Close[0]-ExtremumPrice)/_Point;      
      }   
   else return -1.0;
   }

Serideki emirler arasında gerekli adımı korumak için bu fonksiyona ihtiyacımız vardır. Bu adım sabit olacaktır. "Close[]" dizisinin MQL5'te uygulanmadığını ve önceki makalelerimde gösterildiği gibi bağımsız olarak uygulanması gerektiğini unutmayın. Bu adımın oldukça net olduğunu düşünüyorum.

Mevcut X ve D değerlerini hesaplamak için, diğer tüm fonksiyonlar gibi geri dönüş değeri olmayan aşağıdaki fonksiyonu kullanacağız. Sonucu global değişkenlere yazacaktır (emirlere erişimi en aza indirmek ve geçmişle çalışan fonksiyonların gereksiz çağrılarından kaçınmak daha iyidir):

double Xx;//shift of X
double Dd;//desired rollback of D
void CalcXD()//calculate current X and D
   {
   bool ord;
   bool bStartDirection=false;
   bool bFind=false;
   double ExtremumPrice=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL ) bStartDirection=false;
         if ( OrderType() == OP_BUY ) bStartDirection=true;
         ExtremumPrice=OrderOpenPrice();
         bFind=true;
         break;
         }
      }   
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                        
      if ( OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         if ( OrderType() == OP_BUY && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         }
      }
   Xx=0.0;
   Dd=0.0;   
   if ( bFind )
      {
      if ( !bStartDirection ) Xx=(Close[0]-ExtremumPrice)/_Point;
      if ( bStartDirection ) Xx=(ExtremumPrice-Close[0])/_Point;
      if ( MODEE==MODE_SINGULARITY ) Dd=D(DE,KE,XE,Xx);
      else Dd=Xx*KE;
      }      
   }

Bu kod MT4Orders kütüphanesi ile tamamen uyumludur ve tıpkı aşağıda verilecek fonksiyonlar gibi MQL5'te sorunsuz bir şekilde derlenebilir. Algoritmanın girdi değişkenleri sarı renkle vurgulanmıştır.

Mevcut ve tahmin edilen kârı hesaplamak için üç değişken kullanacağız:

double TotalProfitPoints=0.0;   
double TotalProfit=0;
double TotalLoss=0;   

Geri dönüş değerleri bu değişkenlere eklenirken, fonksiyonların kendilerinin geri dönüş değerleri olmayacaktır - böylece her seferinde kodun çalışmasını birkaç kez yavaşlatan emir yinelemelerinden kaçınmış oluruz.

Sonraki iki fonksiyondan biri kapanış koşulu için kullanılacak, diğeri ise halihazırda açık olan pozisyonların tahmin edilen kârını hesaplamak için kullanılacaktır:

void CalcLP()//calculate losses and profits of all open orders
   {
   bool ord;
   double TempProfit=0.0;
   TotalProfit=0.0;   
   TotalLoss=0.0;    
   TotalProfitPoints=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         TempProfit=OrderProfit()+OrderCommission()+OrderSwap();
         TotalProfitPoints+=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE));
         if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit;
         else TotalLoss-=TempProfit;
         }
      }
   }
   
void CalcLPFuture()//calculate losses and profits of all existing orders in the future
   {
   bool ord;
   double TempProfit=0;
   TotalProfit=0;   
   TotalLoss=0;    
    
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         TempProfit=OrderProfit()+OrderCommission()+OrderSwap()+(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE)*Dd);
         if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit;
         else TotalLoss-=TempProfit;
         }
      }
   }

Ayrıca, burada emir serisi kapanış koşulu için dayanak fonksiyonu bulunmaktadır:

bool bClose()
   {
   CalcLP();
   if ( TotalLoss != 0.0 && TotalProfit/TotalLoss >= ProfitFactorMin ) return true;
   if ( TotalLoss == 0.0 && TotalProfitPoints >= DE*KE ) return true;
   return false;
   }

Uzman Danışmanı test etme:

MetaTrader 5 için tanımlanan prensibi kullanarak bir Uzman Danışman oluşturdum, çünkü bu yöntem doğru uygulandığında neredeyse tüm makasların, komisyonların ve swapların üstesinden gelebilir. İşte ortalama alma prensibinden yararlanan Uzman Danışmanın test sonucu:

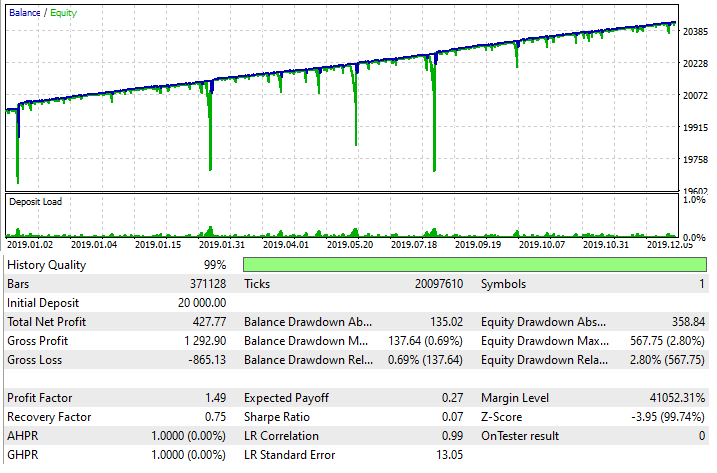
Ancak, bunun yalnızca çok dikkatli kullanılması gereken bir ticaret tekniği olduğunu lütfen unutmayın. Bununla birlikte, çok esnektir ve çok çeşitli stratejilerle birlikte kullanılabilir. Tekrar ediyorum, lütfen dikkatli olun.

Bir ticaret tekniğinin tutarlılığının doğrudan ve dolaylı işaretleri

Bu makale çerçevesinde, geriye dönük testin hangi matematiksel değişkenlerinin, kullanılan tekniğin stratejimizi güçlendirip güçlendirmediği veya hatta zarar oluşturan bir stratejiyi kârlı bir stratejiye dönüştürüp dönüştürmediği hakkında bilgi sağlayabileceğini incelemek faydalı olacaktır. Bu konu çok önemlidir, çünkü geriye dönük test sonuçlarını yanlış yorumlarsak, gerçekten çalışan bir tekniği dışlayabilir veya yanlış bir tekniği kullanabiliriz. Yeni ticaret teknikleri geliştirirken her zaman iki kuralı takip ederim; bu kurallar, çalışan tekniklerin en olası şekilde tespit edilmesi ve yanlış olanların en olası şekilde reddedilmesi için gerekli ve yeterli bir koşul oluşturur:

1. İstatistiksel değerlendirme için veri örnekleminin büyüklüğünün yanı sıra geriye dönük testteki işlem sayısı da en üst düzeye çıkarılmalıdır
2. Geriye dönük test değerlerindeki küçük bir değişiklik bile olumlu değişikliklere işaret edebilir

Çoğu durumda, herhangi bir olumlu değişiklik ticaret için yararlı olacak şekilde güçlendirilebilir. İnkar edilemez avantajları vardır:

1. Bu tür ticaret teknikleri herhangi bir ticaret enstrümanı üzerinde çalışabilir
2. Teknikler birleştirilebilir ve hibrit hale getirilebilir
3. Doğru kullanıldığında, kâr elde etme şansınız, makas varlığında bile zarar etme şansınızdan daha yüksektir

Şimdi bir ticaret tekniği kullanmaya çalışırken hangi değişkenlerin analiz edilmesi gerektiğini göstereceğim. Bu makalede ele alınan son ticaret tekniği örneğini kullanalım. Geriye dönük test ölçütleriyle başlayalım ve iyileştirmeleri tespit etmek üzere sentetik ölçütler oluşturmak için onları nasıl kullanacağımızı görelim.

Öncelikle aşağıdaki değişkenlere dikkat edin:

• Nihai geriye dönük test kârı
• Maksimum bakiye düşüşü
• Maksimum varlık düşüşü

Yardımcı olabilecek, ancak strateji sınayıcı raporlarında bulunmayan bazı ek, daha doğru değişkenler vardır:

• Ortalama bakiye düşüşü
• Ortalama varlık düşüşü

Bu ölçütler neden sistemin ne kadar güvenli ve kârlı olduğunu doğru bir şekilde göstermektedir? Mesele şu ki, herhangi bir geriye dönük test için, demo veya gerçek hesapta ticaret yapan herhangi bir ticaret sisteminde olduğu gibi, aşağıdaki matematiksel ifadeler vardır:

• {i = 0 ... 1 ... 2 ... m} - yükselen yarım dalga sayısı (bu yarım dalga, büyüyen bir varlık veya bakiye segmentidir (bu yükselen yarım dalgayı düşen bir yarım dalga takip eder))
• {j = 0 ... 1 ... 2 ... k} - düşen yarım dalga sayısı (bakiye segmentleri pozisyon açma ve kapama noktasında başlar ve biter, varlık segmentleri de diğer noktalarda biter ve başlar)
• {OrderProfit[j]-OrderComission[j]-OrderSwap[j] < 0 !  Lim(m-->+infinity)[Summ(i)[Summ(j)[OrderProfit[j]-OrderComission[j]-OrderSwap[j]]]/m] = komisyon ve swap hariç toplam kâr} - geriye dönük test veya bakiye için ortalama düşüş
• {SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] < 0 !  Lim(m-->+infinity)[ Summ(i)[Summ(j)[SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j]]]/m] = komisyon ve swap hariç toplam kâr  } - geriye dönük test veya varlık için ortalama düşüş

Başka bir deyişle, işlem maliyeti sıfır olsaydı, stratejinin demo veya gerçek hesapta sonsuz bir geriye dönük test veya sonsuz kullanımı ile hem bakiye hem varlık açısından ortalama düşüş, nihai bakiyenin değerine eğilim gösterir. Elbette bu, yalnızca stratejinin belirgin bir pozitif kârı olduğunda geçerlidir. Toplam kâr negatif işarete sahipse varsa, negatif segmentleri değil, pozitif olanları toplamanız gereken ayna formülleri kullanabilirsiniz. Ancak, halihazırda bilinen pozitif bir geriye dönük test ile çalışmak ve daha sonra buna bazı teknikler uygulamak en uygunudur. Ama bu, global bir geriye dönük testin kâr göstereceği anlamına gelmez. Stratejinin kâr gösterdiği bu tür geçmiş aralıklarını bulmalısınız (tercihen bu tür birkaç aralık).  

Şimdi basit bir martingale kullanarak istikrarını nasıl güçlendirebileceğimizi ve performansını nasıl hafifçe kâra doğru kaydırabileceğimizi görelim. Yukarıda verilen formüllere dayanarak, ticaret tekniğinin ticaret üzerindeki etkisini birkaç küçük segment çerçevesinde bir bütün olarak değerlendirmenin mümkün olduğu bu tür sentetik ölçütler hazırlamak mümkündür:

Sentetik ölçütler için girdi verileri:

• {Tp} - geriye dönük testin veya ticaretin nihai kârı
• {BdM} - ortalama bakiye düşüşü
• {EdM} - ortalama varlık düşüşü
• {BdMax} - maksimum bakiye düşüşü
• {EdMax} - maksimum varlık düşüşü

Renk, geriye dönük testte mevcut olmayan verileri vurgulamaktadır. Ancak bu veriler kodda hesaplanabilir ve ticaretin veya geriye dönük testin sonunda görüntülenebilir. Ancak ben mevcut olan diğer verileri kullanmayı tercih ediyorum. Mesele şu ki, ortalama düşüş ne kadar küçük olursa, çoğu durumda her iki değerden de maksimum düşüş o kadar küçük olur. Bu değerler olasılıklarla çok yakından bağlantılıdır ve bir ölçütteki değişiklikler genellikle başka bir ölçütte yaklaşık orantılı değişikliklere neden olur. 

Sentetik ölçütler:

• {A = Tp/BdM} - strateji geleceği tahmin edemiyorsa bire eşittir; tahmin edebiliyor ve kazanç sağlıyorsa birden büyüktür (bu, kârlılığı hakkındaki soruyu yanıtlamaya eşdeğerdir)
• {B = Tp/EdM} - önceki değerle aynıdır
• {C = Tp/BdMax} - bu ölçütte bir artış varsa, tekniğin yöntemin etkinliğini artırdığı sonucuna varabiliriz (azalma olumsuz etki anlamına gelir)
• {D = Tp/EdMax} - önceki değerle aynıdır

Bu 4 kriterden herhangi biri kullanılabilir. Bunlardan ilk ikisi daha doğrudur, ancak geriye dönük test onları hesaplamak için gerekli verileri sağlayamaz, bu nedenle girdi verilerini kendiniz okumanız gerekir. Diğer ikisi, geriye dönük testten elde edilen değerler kullanılarak hesaplanabilir. Ben şahsen son iki ölçütü kullanıyorum çünkü onlar mevcuttur ve kolayca bulunabilir. Şimdi, durma emirleriyle kapanan basit bir martingale örneğini temel alarak bu yöntemin uygulanmasını görelim. Son ilginç yaklaşımı kullanarak değişkenlerini güçlendirmeye çalışacağız.

Bakiye ve varlık dalgalarını kullanma

Aslında, bu teknik sadece martingale için değil, aynı zamanda yeterince yüksek işlem frekansına sahip diğer stratejiler için de kullanılabilir. Bu örnekte, bakiye düşüşüne dayalı ölçütü kullanacağım. Çünkü bakiye ile ilgili her şey daha kolay değerlendirilir. Bakiye grafiğini yükselen ve düşen segmentlere ayıralım. İki komşu segment bir yarım dalga oluşturur. Yarım dalgaların sayısı, işlem sayısı sonsuza doğru gittikçe sonsuza doğru gider. Martingale'i biraz daha kârlı hale getirmemiz için sonlu bir örneklem yeterli olacaktır. Aşağıdaki diyagram bu fikri açıklamaktadır:

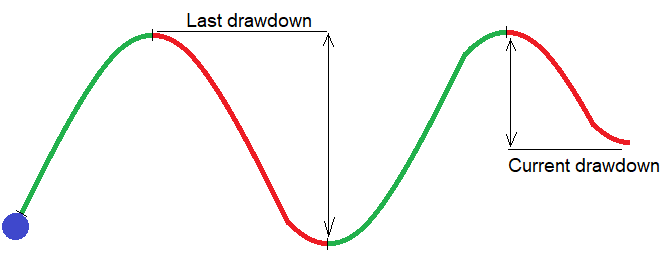
Şekilde oluşmuş ve yeni başlamış bir yarım dalga görünmektedir. Herhangi bir bakiye grafiği bu tür yarım dalgalardan oluşur. Bu yarım dalgaların büyüklüğü sürekli dalgalanır ve grafikte bu tür yarım dalga gruplarını her zaman ayırt edebiliriz. Bu yarım dalgaların büyüklüğü bir dalgada daha küçük, diğerinde ise daha büyüktür. Dolayısıyla, lotu kademeli olarak düşürerek, mevcut grupta kritik bir düşüşe sahip bir yarım dalga görünene kadar bekleyebiliriz. Bu kritik düşüşün lotu seride minimum olacağından, bu tüm dalga gruplarının genel ortalama ölçütlerini artıracak ve sonuç olarak orijinal testin aynı performans değişkenleri de artacaktır.

Uygulama sırasında martingale için iki ek girdi parametresine ihtiyacımız olacaktır:

• {DealsMinusToBreak} - döngünün başlangıç lotunu başlangıç değerine sıfırladığımız bir önceki döngü için zararda olan işlem sayısı
• {LotDecrease} - işlem geçmişinde yeni bir döngü ortaya çıktığında döngünün başlangıç lotunu azaltma adımı

Bu iki parametre, güvenli yarım dalga grupları için artırılmış lotlar ve tehlikeli yarım dalga grupları için azaltılmış lotlar sağlamamıza olanak tanıyacak ve bu da teorik olarak yukarıda belirtilen performans ölçütlerini artıracaktır.

Aşağıdaki kod martingale Uzman Danışmanına eklenecektir. Bir sonraki döngünün başlangıç lotunu hesaplar ve gerekirse sıfırlar.

Kod:

double DecreasedLot=Lot;//lot to decrease
double CalcSmartLot()//calculate previous cycle
   {
   bool ord;
   int PrevCycleDeals=0;
   HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent());
   for ( int i=HistoryDealsTotal()-1; i>=0; i-- )
      {
      ulong ticket=HistoryDealGetTicket(i);
      ord=HistoryDealSelect(ticket);
      if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
      && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
      && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
         {
         if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) > 0 )
            {
            for ( int j=i+1; j>=0; j-- )//found a profitable deal followed by losing (count them)
                {
                ticket=HistoryDealGetTicket(j);
                ord=HistoryDealSelect(ticket);
                if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
                && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
                && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
                   {
                   if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 )
                      {
                      PrevCycleDeals++;
                      }
                   else
                      {
                      break;
                      }
                   }                
                }
            break;    
            }
         else
            {
            break;
            }
         }
      }
      
   if ( PrevCycleDeals < DealsMinusToBreak ) DecreasedLot-=LotDecrease;
   else DecreasedLot=Lot;
   if ( DecreasedLot <= 0.0 ) DecreasedLot=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);

   return DecreasedLot;
   }

Girdi parametreleri sarı renkle vurgulanmıştır. Lütfen bunun bir test fonksiyonu olduğunu ve bu haliyle yalnızca strateji sınayıcıda test için uygun olduğunu unutmayın. Ancak bu varsayımın ilk kaba ve basit testini yapmamız yeterli olacaktır. Makale yalnızca fikri anlamak için gereken minimum kodu sunmaktadır. Gereksiz düşüncelerle okuyucunun dikkatini dağıtmamak adına Uzman Danışman kodunun geri kalanını vermeyeceğim. Aynı durum, makalenin yazımı sırasında oluşturulan diğer Uzman Danışmanlar için de geçerlidir. Şimdi normal martingale’i test edelim ve ardından yeni modu açıp performans değişkenlerini nasıl etkilediğini görelim. Bu Uzman Danışman, MetaTrader 5 için de tasarlanmıştır, çünkü ilk sinyal, farklı makaslarla aynı performansı gösteren normal bir martingale’dir.

Uzman Danışmanı test etme:

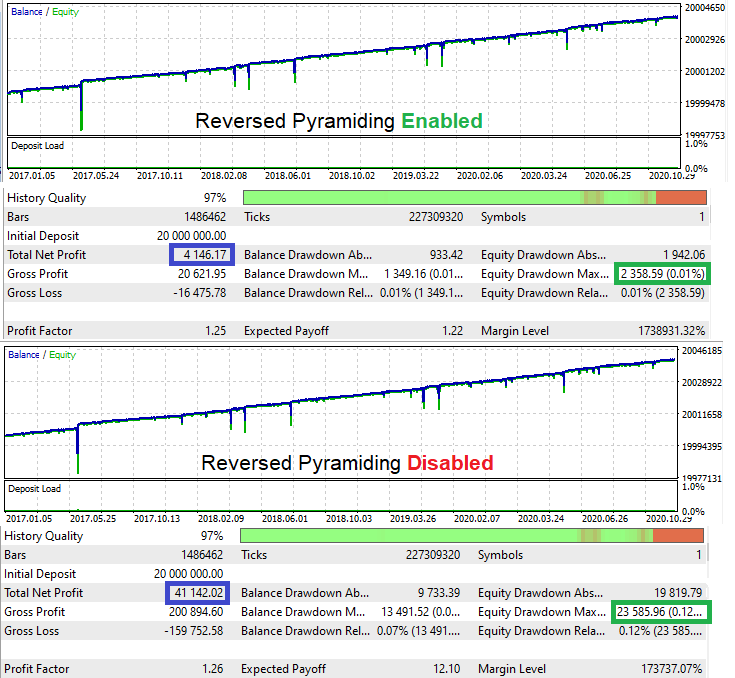
Orijinal test için D'yi hesaplarsak, 1.744 değerini alacaktır. Yeni mod etkinleştirildiğinde bu değer 1.758 olur. Kârlılık hafifçe doğru yöne kaymıştır. Elbette birkaç test daha yaparsak bu değer düşebilir, ancak ortalama olarak değişkende bir artış olmalıdır. Açık konuşmak gerekirse, mantık iyi seçilmemiştir, ancak açıklama amaçlı yeterlidir.

Sonuç

Bu makalede, otomatik ticaret sistemi geliştiricileri için yararlı olabilecek en ilginç ve yararlı teknikleri toplamaya çalıştım. Bu tekniklerden bazıları, uygun çalışma ve araştırmadan sonra kârın artırılmasına yardımcı olabilir. Umarım bu materyal faydalı olmuştur. Bu teknikler bir araç kutusu olarak düşünülebilir, ancak bir Kutsal Kasenin nasıl inşa edileceğine dair bir kılavuz değildir. Bu tür tekniklerle basit bir tanışıklık bile sizi acele yatırımlardan veya kritik zararlardan kurtarabilir. Daha fazla zaman ve çaba harcayarak, iki göstergenin çaprazlamasına dayanan geleneksel bir ticaret sisteminden daha ilginç ve istikrarlı bir şey yaratmaya çalışabilirsiniz.