Grid ve martingale: bunlar nedir ve nasıl kullanılır?

Giriş

Bu makalede, bu stratejileri incelemek ve kârlılıklarını değerlendirmek için matematik ve programlama kullanacağım. Makalede bir matematiksel bölüm ve bir de pratik bölümü yer alacaktır. Matematiksel bölümde, stratejilerin beklenen getirisini ve birçok yatırımcı tarafından dikkate alınmayan diğer önemli parametreleri hesaplamak için denklemler sunacağım. Pratik bölümünde ise basit bir grid ve martingale geliştireceğim ve denklemleri gerçeklikle karşılaştıracağım. Bu makale özellikle yeni başlayanlar için faydalıdır çünkü bu stratejiler genellikle ilk karşılaştıkları stratejilerdir. Onlara körü körüne inanmak, zamanında benim de başıma geldiği gibi, hayal kırıklıklarına ve zaman kaybına yol açabilir. Matematiği bilmeseydim, belki de hala onlara inanıyor olurdum. Ancak bu stratejilere doğru bir şekilde bakarsanız hala bir mantığı vardır. İşte bunu kanıtlayacağım.

Bu iki stratejinin ortak noktası nedir?

Bu iki stratejinin popülerliğini anlamak için, tüm acemi Forex yatırımcılarının ne istediğine bir göz atmalıyız. Çoğu acemi yatırımcı, zekalarının hızlı ve kolay bir şekilde zengin olmalarına yardımcı olabileceğini düşünen matematikçiler ve hayalperestlerdir. Ben de bir zamanlar böyle bir hayalperesttim. Bu stratejilerin her ikisi de, strateji sınayıcıda sürekli yükselen grafikler şeklinde kârlı ticaret görünümü verir. Fiyat geçmişinin birçok bölümünde, sınayıcı herhangi bir filtre olmadan bile Kutsal Kase benzeri sonuçlar gösterebilmektedir. Herhangi bir faaliyet alanında ve herhangi bir işte, daha bilgili kişilerin sizin zararınıza kendilerini zenginleştirme tehlikesi vardır. Forex ticareti de bir istisna değildir. Forex'te bu tür aldatıcı uygulamalar bol miktarda bulunmaktadır ve bu iki strateji bunun en açık ve popüler kanıtıdır. Bu stratejileri ilk kez kullandığınızda, inanılmaz kâr faktörleri ve beklenen getirilerle tüm döviz çiftlerinde çalıştıklarını ve hatta herhangi bir makas ile başa çıkabildiklerini göreceksiniz, bu nedenle bu algoritma piyasanın ötesinde görünmektedir. Bunun nedeni, saf matematiğe dayanmaları ve mantıksız olmalarıdır. Bunca yıl sonra bile, fiyat yönünden bağımsız olarak her zaman kâr elde etmemi sağlayan algoritmalar bulmak istiyorum. Matematikçiler genellikle ilginç insanlardır. Gerçekte doğru olup olmadığına bakmaksızın uygun denklemlerle her şeyi kanıtlayabilirler. Genel olarak bu iki strateji, sizi kendilerini kullanmaya ikna etmek için breakeven yanılsamasından yararlanır. Her ikisi de herhangi bir döviz çifti ve herhangi bir zaman dilimi üzerinde çalışır veya daha doğrusu çalışma yanılsaması yaratır ve sizi basitliklerine ve etkinliklerine ikna eder. Bu stratejileri araştırırken, er ya da geç hiçbir şey bilmediğinizi fark edeceksiniz. Ancak, rasyonel düşünmeye başlamanın ve piyasanın gerçek doğasını ve gerçekten hangi stratejileri kullanmanız gerektiğini anlamanın tek yolu bu olduğu için bu aşama gereklidir.

Grid ve temel denklemleri

Grid, herhangi bir piyasada kâr elde etmek amacıyla oluşturulmuştur. Düşüyor ya da yükseliyor olması fark etmez, eğer piyasada açıkça görülebilen bir hareket varsa, o zaman fikir çerçevesinde, grid akıllı bir emir açma sistemi kullanarak emirler açar, böylece toplamda bu emirler bir noktada hepsinin bir kerede kapatılması için yeterli kâr elde eder. Bunu aşağıdaki görüntülerde göstereyim:

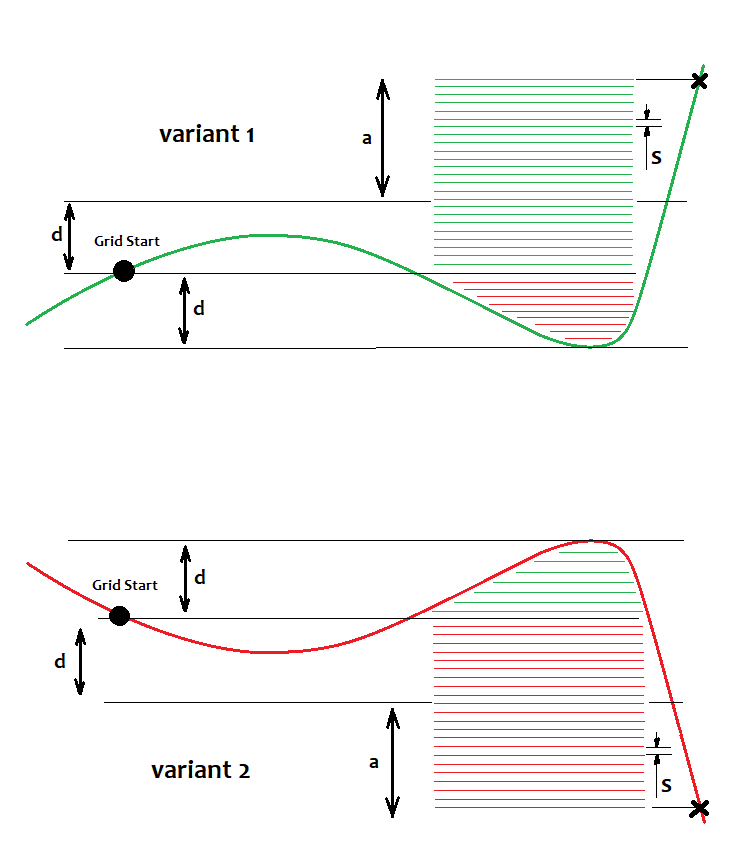
Burada sırasıyla yükselen ve düşen piyasalar için iki seçenek gösterdim. Grid stratejisine göre, hangi seçeneği seçersek seçelim kazanmalıyız. Grid’i kullananlar her zaman en iyi fiyattan tetiklendikleri için bekleyen emirleri kullanmayı söylerler. Bu doğrudur, ancak piyasa emirlerinin daha kötü olmadığına inanıyorum (giriş sırasında makası ve kaymayı kontrol edebildiğiniz gerçeğiyle). Ayrıca, girişi biraz erteleyebilirsiniz. Ancak, limit emirleri bu stratejide daha iyidir. Emirlerin verildiği bir başlangıç noktamız vardır. Bu noktanın üzerinde, "s" adımıyla alış emirleri belirlerken, altında satış emirleri belirleriz. Fiyat onlara ulaşırsa, piyasa emirlerine dönüşürler. Görüntü, belirli fiyatlama durumuna göre halihazırda açık emirleri göstermektedir. Burada limit emirlerini görüntülemenin bir anlamı yoktur, çünkü süresiz olarak yukarı ve aşağı giderek aynı seviyelerde kalırlar. Sadece açık gerçek emirler bizim için önemlidir, çünkü onların kâr veya zararı sırasıyla toplam kâr veya zararı oluşturur. Kâr sağlamak için, bazı emirler diğerlerinden "K" kat daha büyük olmalıdır, yani K >= K0 olduğu yerde K = a/d sağlamalıyız. К0'a ulaşıldığında, tüm grid emirlerinin toplam kârı sıfır eşiğini aşar. MetaTrader 4 durumunda bir pozisyonun veya emirlerin mevcut kârını da aynı basit şekilde hesaplayabiliriz. Aksi takdirde, fiyat hemen belirli bir yönde hareket ettiğinde bir durumla karşılaşırız ve fiyat "n" puan yukarı veya aşağı hareket ettikten sonra kârı alırız. Açıkçası, bu katsayı hesaplanabilir ancak manuel olarak kolayca seçilebilir. Olası hesaplama aşağıdaki gibidir:

• Nl = d/s-1
• NP = (a+d)/s-1
• Pr = Sum(1,NP)(s*i) = (s+s*NP)*Np/2
• Ls = Sum(1,Nl)(s*j+s*NP) = (s+s*Nl)*Nl/2+s*NP^2

Tüm emirlerin zarar veya kârını topladığımızda, bu toplamların aritmetik ilerleme olduğunu görebiliriz. Aritmetik ilerlemenin toplamını (ilk ve son terimlerini kullanarak) tanımlayan bir denklem vardır ve bu denklem burada uygulanır.

Pr-Ls = 0 kabul edildiğinde, bu denklem çözüldüğünde "a" elde edilir ve ardından K0 = a/d hesaplanabilir. Ayrıca, bu denklemlerin kullanılması, açık alış ve satış pozisyonlarını içeren ticaret döngülerinin kâr faktörünü ve beklenen getirisini tanımlamaya olanak tanır.

• Prf = Pr/Ls 
• M = (Pr-Ls)/(Np+Nl)

Bu denklemler, grafiğin tamamı yerine belirli bir ticaret döngüsünün kâr faktörünü ve beklenen getirisini hesaplar. Grafiğimizin döngünün son noktasında sona ermesi koşuluyla, kâr faktörü pozitif olacaktır. Bir döngü ayrı bir grid’dir. Grid oluşturulur, mümkün olan maksimum ölçüde kullanılır, pozisyonlar kapatılır ve yeni bir grid oluşturulur. Sonsuz bakiye durumunda bu sonsuz bir süreçtir. Bakiye eğrisinde yaklaşık olarak şu şekilde görünür:

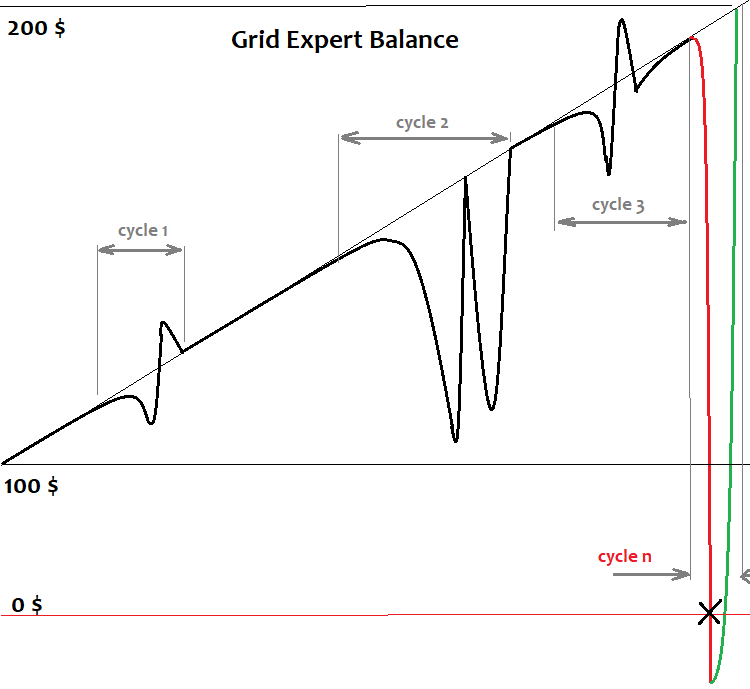
Burada, geçmiş boyunca çalışan bir grid robotunun bakiye grafiğinin basitleştirilmiş bir temsilini sundum. Bakiyenin dayanabildiği ve grafiğin yükseldiği birkaç döngü vardır. Ancak bu kaçınılmaz olarak, bakiyenin yetersiz olduğu ve tüm görünür kârımızın brokera gittiği bir döngü ile sona erer. Matematik açısından bu, tamamlanmamış bir döngü olarak kabul edilir. Tamamlanmamış bir döngü her zaman kârsızdır ve zararı, sonuna kadar çalışan döngüler sırasında kazanılan tüm kârın üzerine biner. Döngü, grid’i devam ettirmek için gerekli emir miktarının yetersiz olması nedeniyle de tamamlanamayabilir. Tüm brokerlar, terminalde veya belirli bir çiftte aynı anda açık olan emirlerin sayısına sınır koyar. Grid sonsuza kadar inşa edilemez. Bunu yapabildiğimizi varsaysak bile, yine de eninde sonunda yukarıdaki sonucu elde ederiz. Makalenin sonunda bunun nedenini matematik açısından kısaca açıklayacağım.

Martingale ve temel denklemleri

Grid gibi, martingale'in arkasındaki fikir de piyasanın yönünden bağımsız olarak kazanmaktır. Aynı sonsuz kâr yanılsamasına dayanmaktadır. Bir emir açarsak ve kârlı çıkarsa, daha fazla işlem yaparız. Zarar ettiğimiz anda, bir sonraki emrin lotunu kaybettiğimiz pozisyona göre "n" kat artırırız. Emrimiz kârlıysa, basitçe kapatır ve lotu başlangıç değerine geri sıfırlarız. Emrin tekrar zarar ettirdiği ortaya çıkarsa, döngü içerisindeki tüm kaybettiren pozisyonların lotlarının toplamına göre lotu "n" kat artırarak önceki adımı tekrarlarız. Tekrar kârlı bir işlem elde edene kadar bunu tekrarlarız. Döngüdeki son işlem her zaman kârlıdır ve kârı her zaman kaybedilen işlemlerin zararını karşılar. Grafik bu şekilde döngülerden oluşmaya başlar. Grafiğin son döngü ile sona ermesi koşuluyla, pozitif bir beklenen getiri ve kâr faktörü elde ederiz. Bu emirleri nasıl ve nerede açtığımızın hiçbir önemi yoktur. Tercihen, bu emirler sabit kâr ve zarara sahip olmalı veya sadece sabit durma seviyelerinde kapanmalıdır. İşte martingale robotunun bakiye grafiğinin nasıl göründüğü:

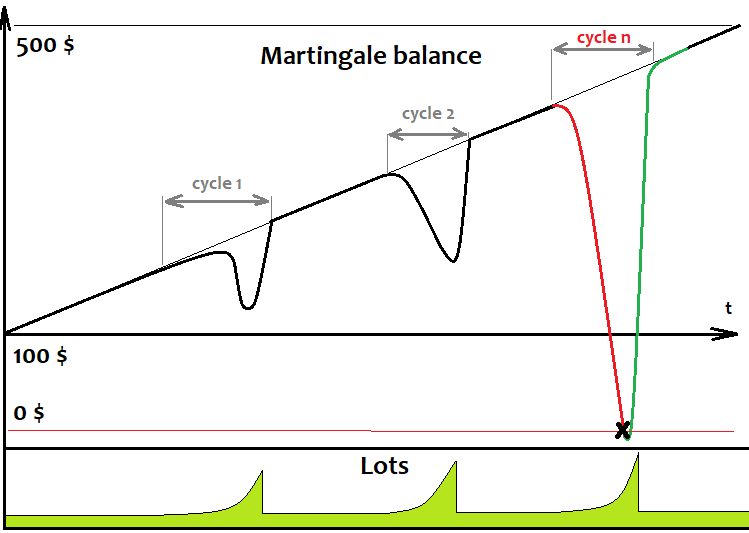
Gördüğümüz üzere, martingale tıpkı grid gibi döngüler halinde çalıştığı için grid bakiye grafiğine çok benzemektedir. Tek fark, her zaman tek bir emir açar ve bir sonrakini açmak için kapanana kadar bekler. Tıpkı grid durumunda olduğu gibi, er ya da geç bakiye döngüyü bitirmek için yetersiz kalır, tüm emir kapatılır ve bakiye silinir. Kârlı döngüler sağlamak için, son işlemin kârı öncekilerin zararını karşılamalıdır:

• Nl
• Np = 1
• Pr = L[Nl+Np]*TP[Nl+Np]*TickSize
• Ls = Sum(1,Nl)(L[i]*SL[i])*TickSize

Burada kâr, sistem lot büyüklüğü ile ilgilendiğinden, puan yerine işlem hesabınızın para birimi cinsinden hesaplanır. Belirli bir sıradaki lotlar özyineleme kullanılarak hesaplanır:

• L[1] = StartLot
• for(2,Nl)L[i] = (K*Sum(1,i-1)(L[j]*SL[j]))/TP[i]

Burada "K" döngünün gerekli kâr faktörüdür. Makas, komisyon ve swap burada dikkate alınmamıştır ancak bunun önemli olduğunu düşünmüyorum. İhtiyaç duyulması halinde denklemler kolaylıkla değiştirilebilir, ancak bunda bir anlam görmüyorum. Martingale denklemlerini grid denklemlerine benzer hale getirmeye çalıştım. SL ve TP, emrin elde edilen zararı ve istenen kârıdır. Aşağıdaki basit denklemi çözerek tanımı elde edebiliriz: K = (L[i]*TP[i])/Sum(1,i-1)(L[j]*SL[j])

En basit grid Uzman Danışmanının geliştirilmesi ve test edilmesi

Yukarıdaki varsayımları test etmek için MQL5 dilinde basit bir grid Uzman Danışmanı ve basit bir martingale yazalım ve sonuçları görelim. Grid ile başlayacağım. İlk olarak, şablonumuza pozisyonlarla çalışmak için birkaç kullanışlı sınıf ekleyelim:

#include <Trade\PositionInfo.mqh>
#include <Trade\Trade.mqh>
CPositionInfo  m_position=CPositionInfo();// trade position object
CTrade         m_trade=CTrade();          // trading object

Bu iki kütüphane MetaTrader 5'te varsayılan olarak her zaman mevcuttur, bu nedenle derleme sorunu olmayacaktır. 

Daha sonra, gerekli tüm girdileri tanımlayalım:

///grid variables
input int MaxChannelSizePoints=500;//Max Of a+d
input int MinMoveToClose=100;//Mininum Move
input int GridStepPoints=20;//Grid Step In Points
input int BarsI=999;//Bars To Start Calculate
input double KClose=3.5;//Asymmetry
///

////////minimum trading implementation
input int SlippageMaxOpen=15; //Slippage For Open In Points
input double Lot=0.01;//Lot
input int MagicC=679034;//Magic
/////////

İlk blok gerekli tüm grid parametrelerini uygularken, ikincisi en basit haliyle sabit bir lotla işlem gerçekleştirme yeteneğini uygular.

Uzman Danışmanı başlatırken, çalışmanın yanlış sonlandırılması durumunda önceki oturumdaki grid parametrelerinin doğrulanmasına ve kurtarılmasına ihtiyacımız olacaktır. Bu özellik isteğe bağlıdır ancak bu tür şeyleri önceden uygulamak daha iyidir:

void DimensionAllMQL5Values()//////////////////////////////
   {
   ArrayResize(Time,BarsI,0);
   ArrayResize(High,BarsI,0);
   ArrayResize(Low,BarsI,0);
   }

void CalcAllMQL5Values()///////////////////////////////////
   {
   ArraySetAsSeries(High,false);                        
   ArraySetAsSeries(Low,false);                              
   ArraySetAsSeries(Time,false);                                                            
   CopyHigh(_Symbol,_Period,0,BarsI,High);
   CopyLow(_Symbol,_Period,0,BarsI,Low);
   CopyTime(_Symbol,_Period,0,BarsI,Time);
   ArraySetAsSeries(High,true);                        
   ArraySetAsSeries(Low,true);
   ArraySetAsSeries(Time,true);
   }

Bu kod, ilk analizi tamamlamak adına önceden tanımlanmış dizileri uygulamak için gereklidir. Bu dizilere daha sonra ihtiyacımız olmayacaktır. Onları yalnızca ilk hesaplama sırasında kullanacağız.

Kurtarma işlemi aşağıdaki şekilde gerçekleştirilir:

void RestoreGrid()//recover the grid if the robot is restarted
   {
   DimensionAllMQL5Values();
   CalcAllMQL5Values(); 
   bool ord=PositionSelect(Symbol());
   if ( ord && int(PositionGetInteger(POSITION_MAGIC)) == MagicC )
      {
      GridStartTime=datetime(PositionGetInteger(POSITION_TIME));
      GridStartPrice=double(PositionGetDouble(POSITION_PRICE_OPEN));
      GridUpPrice=GridStartPrice;
      GridDownPrice=GridStartPrice;      
      
      for(int i=0;i<BarsI;i++)
         {
         if ( High[i] > GridUpPrice ) GridUpPrice=High[i];
         if ( Low[i] < GridDownPrice ) GridDownPrice=Low[i];
         if ( Time[i] < GridStartTime ) break;         
         }
      bCanUpdate=true;
      bTryedAlready=false;         
      }
   }

Grid’in mevcut durumunu izlemek için, grid’in var olduğu süre boyunca üst ve alt fiyatları, grid’in başlangıç fiyatını ve ayarlandığı zamanı gösteren ek değişkenlere ihtiyacımız vardır.

datetime GridStartTime;//grid construction time
double GridStartPrice;//grid starting price
double GridUpPrice;//upper price within the corridor
double GridDownPrice;//lower price within the corridor

Ayrıca, fiyat hareketi sırasında grid değişkenlerini izlemek veya güncellemek ve ilk girişim başarısız olursa grid’i kapatmak adına ek girişimler yapmak için iki boolean değişkenine ihtiyacımız vardır.

bool bCanUpdate;//whether it is possible to update the grid
bool bTryedAlready;//whether there was an attempt to close a position

Geliştirme sırasında grid parametrelerinin oluşturulması ve güncellenmesi aşağıdaki gibi görünmektedir:

void CreateNewGrid()//create a new grid
   {
   SymbolInfoTick(Symbol(),LastTick);  
   GridStartTime=TimeCurrent();
   GridStartPrice=LastTick.bid;
   GridUpPrice=GridStartPrice;
   GridDownPrice=GridStartPrice;
    
   double SummUp=LastTick.ask+double(GridStepPoints)*_Point;
   double SummDown=LastTick.bid-double(GridStepPoints)*_Point;
   
   while ( SummUp <= LastTick.ask+double(MaxChannelSizePoints)*_Point )
      {
      m_trade.BuyStop(Lot,SummUp,Symbol());
      SummUp+=double(GridStepPoints)*_Point;
      }
     
   while ( SummDown >= LastTick.bid-double(MaxChannelSizePoints)*_Point )
      {
      m_trade.SellStop(Lot,SummDown,Symbol());
      SummDown-=double(GridStepPoints)*_Point;
      }
   }

void UpdateGrid()//update the grid parameters
   {
   SymbolInfoTick(Symbol(),LastTick);
   if ( LastTick.bid > GridUpPrice ) GridUpPrice=LastTick.bid;
   if ( LastTick.bid < GridDownPrice ) GridDownPrice=LastTick.bid;
   }

Pozisyonları kapatma ve kalan limit emirlerini temizleme fonksiyonlarının yanı sıra grid’i kapatma koşulunu tespit eden dayanak fonksiyonu:

void ClosePosition()//close a position by a symbol
   {
   bool ord;
   ord=PositionSelect(Symbol());
   if ( ord && int(PositionGetInteger(POSITION_MAGIC)) == MagicC  )
      {
      if(m_position.SelectByIndex(0)) m_trade.PositionClose(m_position.Ticket());          
      }
   }

void CleanLimitOrders()//clear limit orders
   {
   int orders=OrdersTotal();
   for(int i=0;i<orders;i++)
      {
      ulong ticket=OrderGetTicket(i);
      if(ticket!=0)
         {
         m_trade.OrderDelete(ticket);
         }
      }
   }

bool bCanClose()//closure condition
   {
   if ( GridStartPrice == GridUpPrice && (GridStartPrice-GridDownPrice)/_Point >= MinMoveToClose ) return true;
   if ( GridStartPrice == GridDownPrice && (GridUpPrice-GridStartPrice)/_Point >= MinMoveToClose ) return true;
   
   if ( GridStartPrice != GridUpPrice && GridStartPrice != GridDownPrice 
   && (GridStartPrice-GridDownPrice)/(GridUpPrice-GridStartPrice) >= KClose 
   && (GridStartPrice-GridDownPrice)/_Point >= MinMoveToClose ) return true;
   if ( GridStartPrice != GridDownPrice && GridStartPrice != GridUpPrice 
   && (GridUpPrice-GridStartPrice)/(GridStartPrice-GridDownPrice) >= KClose
   && (GridUpPrice-GridStartPrice)/_Point >= MinMoveToClose ) return true;
   
   /*
   if ( GridUpPrice >= GridStartPrice+MaxChannelSizePoints*_Point 
   //|| GridDownPrice <= GridStartPrice-MaxChannelSizePoints*_Point ) return true;
   */
   return false;
   }

Dayanak fonksiyonundaki son koşulu yorum haline getirdim. Fiyatın grid’in dışına çıkması durumunda grid’i kapatır. İstediğiniz zaman kullanabilirsiniz, başka hiçbir şeyi değiştirmez. Şimdi sadece ana ticaret fonksiyonunu yazmamız gerekiyor:

void Trade()//the main function where all actions are performed
   {
   bool ord=PositionSelect(Symbol());
   
   if ( bCanUpdate ) UpdateGrid();
   
   if ( ord && bCanClose() )//if there is a position and the closing condition is met
       {
       ClosePosition();
       CleanLimitOrders();
       bCanUpdate=false;
       bTryedAlready=true;
       }
   if ( bTryedAlready ) ClosePosition();
          
   if ( !bCanUpdate && !ord )
       {
       CleanLimitOrders();
       CreateNewGrid();
       bCanUpdate=true;
       bTryedAlready=false;
       }
   }

 Ayrıca, Uzman Danışmanı başlatırken nerede ne çağrılacağını ve ne yapılacağını tanımlayalım:

int OnInit()
  {
  m_trade.SetExpertMagicNumber(MagicC);//set the magic number for positions
  RestoreGrid();//restore the grid if present
   return(INIT_SUCCEEDED);
  }

void OnTick()
  {
  Trade();
  }

Grid Uzman Danışmanını geliştirdik. Şimdi onu test edelim ve nasıl davrandığını görelim:

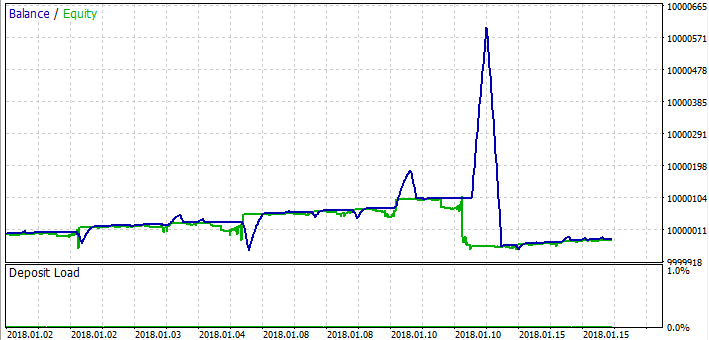
Gördüğünüz gibi, kârsız döngü hakkındaki varsayımlar doğrulandı. İlk başta, grid oldukça iyi çalışmaktadır, ancak daha sonra grid’in yetersiz kaldığı bir an geliyor ve tüm kârı mahveden bir zarar döngüsüne yol açıyor. Trend olan piyasa segmentleri genellikle iyi sonuçlar gösterirken, kayıplar çoğunlukla yatay segmentlerde meydana gelmektedir. Makasa sahip olduğumuz için genel sonuç her zaman zarardır.

En basit martingale Uzman Danışmanının geliştirilmesi ve test edilmesi

Grid’i ele aldığımıza göre, şimdi martingale Uzman Danışmanına geçebiliriz. Kodu çok daha basit olacaktır. Pozisyonlarla çalışmak için, grid Uzman Danışmanında uygulanan kütüphaneleri kullanacağız. Kodu ikinci kez görüntülemenin bir anlamı yoktur. Hemen girdilere bakalım:

input int SLE=100;//Stop Loss Points
input int TPE=300;//Take Profit Points
input int SlippageMaxOpen=15; //Slippage For Open In Points
input double Lot=0.01;//Start Lot
input int MagicC=679034;//Magic
input int HistoryDaysLoadI=10;//History Deals Window Days

Daha fazla basitlik için, pozisyonların katı bir şekilde zararı durdur veya kârı al ile kapatıldığı sistemi seçtim. Son değişken, tüm emir geçmişini sürekli olarak yüklemekten kaçınmamızı, bunun yerine yalnızca gerekli pencereyi yüklememizi sağlar (tamamen optimizasyon için). Diğer değişkenlerin kendi kendini açıkladığına inanıyorum.

Uzman Danışman sadece iki fonksiyona sahip olacaktır:

double CalcLot()//calculate the lot
   {
   bool ord;
   double TotalLot=0;
   HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent());
   for ( int i=HistoryDealsTotal()-1; i>=0; i-- )
      {
      ulong ticket=HistoryDealGetTicket(i);
      ord=HistoryDealSelect(ticket);
      if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
      && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
      && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
         {
         if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 )
            {
            TotalLot+=HistoryDealGetDouble(ticket,DEAL_VOLUME);
            }
         else
            {
            break;
            }
         }
      } 
   return TotalLot == 0 ? Lot: TotalLot;
   }


void Trade()//the main function where all actions are performed
   {
   bool ord=PositionSelect(Symbol());
   SymbolInfoTick(Symbol(),LastTick);
   if ( !ord )
      {
      if ( MathRand() > 32767.0/2.0 )
         {
         m_trade.Buy(CalcLot(),_Symbol,LastTick.ask,LastTick.bid-double(SLE)*_Point,LastTick.ask+double(TPE)*_Point);
         }
      else
         {
         m_trade.Sell(CalcLot(),_Symbol,LastTick.ask,LastTick.ask+double(SLE)*_Point,LastTick.bid-double(TPE)*_Point);
         }
      }
   }

İlki, işlem geçmişine baktıktan sonra bir pozisyon açmak için kullanılan nihai lotu hesaplamak için gereklidir. Eğer son işlem kârlı değilse, bir sonraki lot, ilk kârlı işleme kadar olan önceki kayıp işlemlerin lotlarının toplamına eşit olacaktır. Son işlem kârlıysa, lot başlangıç değerine sıfırlanır. Ana fonksiyonda, sabit durma seviyeleri ile farklı yönlerde rastgele emirler açıyoruz (hacimler ilk fonksiyon kullanılarak hesaplanır). Tüm bunların doğru çalışması için, tıpkı grid’de olduğu gibi, ana fonksiyonu OnTick işleyicisinde çağırmamız ve başlatıcıda Uzman Danışmana bir sihirli sayı atamamız gerekir.

Böylece, en basit martingale geliştirilmiş olur. Şimdi onu test edelim ve nasıl davrandığını görelim:

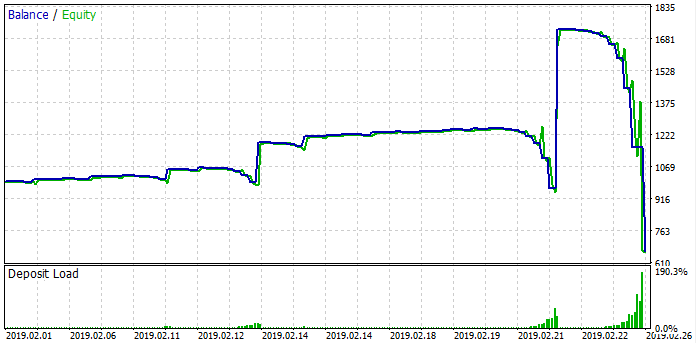
Durum grid’e benzerdir. Döngüleri görebiliyoruz. Martingale Uzman Danışmanı, zarar döngüsü başlamadan önce bir süre boyunca çalışmıştır. Ardından, teminat bir sonraki pozisyonu açmak için yetersiz kalınca zarar meydana gelmiştir. Tıpkı grid gibi, bir yerde çalışır, bir yerde çalışmaz, ama sonunda her zaman zararla sonuçlanır. Şimdi her iki stratejiyi de incelediğimize göre, bizi bu iki stratejiyi anlamaktan daha önemli cevaplara götürecek matematiksel sonuçlar çıkarmanın zamanı geldi.

Grid ve martingale arkasındaki ortak matematik

Grid ve martingale'in arkasındaki ortak matematiğin neden bu kadar önemli olduğuna inanıyorum? Bunu iyice anlarsak, inanmak istesek de bize asla kâr getirmeyecek bir dizi fikre nihayet veda edebiliriz. En azından, hangi koşulların bu stratejilerin performansına katkıda bulunabileceğini anlayacağız. Ayrıca, saf martingale ve grid'in neden kaybettiren stratejiler olduğunu öğreneceğiz.

Herhangi bir stratejinin sonsuz sayıda en basit stratejiden oluştuğunu düşünelim. Bir emir açıldığında, bunlardan biri etkinleştirilir. Bu emirlerin sabit bir zarar veya kârla kapatıldığını varsayacağız. Onları C[i] ve Lot[i] dizilerine karşılık olarak koyalım, bu dizilerin büyüklüğü eşittir ve sonsuza eğilimlidir. Her bir strateji tarafından uygulanan lotun her zaman farklı olduğunu varsayalım. Ayrıca, bu stratejilerden herhangi birinin tetiklenme olasılığını da tanıtalım. PC[i], elbette bu olaylar bir kapsamlı olaylar grubu oluşturur, böylece Sum(0,n)(PC[i]) = 1 olur. Bu olayların tüm sonuçları, sırasıyla zarar ve kâr etkinleşmelerini temsil eden yeni olay uzayları S[i] ve T[i]’yi oluşturur. Bu olayların kendi koşullu olasılıkları PS[i] ve PT[i] vardır ve elbette bunlar da bir kapsamlı olaylar grubu oluşturur. Grafiksel gösterim aşağıda verilmiştir:

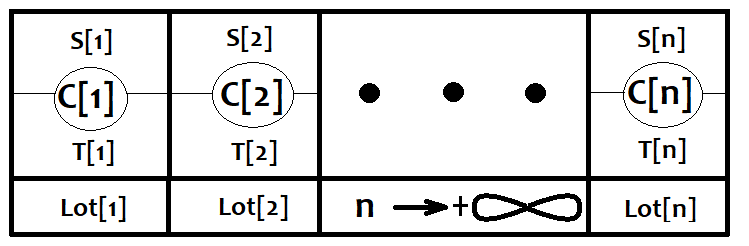
Şimdi bu listeden herhangi bir stratejiyi ele alalım ve beklenen getirisini hesaplayalım.

• M[i] = (PT[i]*TP-PS[i]*SL)*Lot[i]*TickSize

Pozisyon açılış noktalarındaki fiyat yönünü bilmiyorsak, M[i] = 0 diyebiliriz, burada M[i] belirli stratejilerin beklenen getiriler dizisidir. Başka bir deyişle, fiyatın nereye gideceğini bilmiyorsak, işlem sayısının sonsuza gitmesi koşuluyla nasıl işlem gerçekleştirirsek gerçekleştirelim 0 elde ederiz.

Genel beklenen getiri denklemi aşağıdaki gibidir:

• M0 = Sum(0,n)(PC[i]*M[i])

Biliyoruz ki n sonsuza yöneldiğinde, tüm M[i] sıfıra yönelir, yani toplamımızın tüm terimleri, strateji sayısının sonlu, işlem sayısının ise sonsuz olması durumunda 0'a yönelir. Bu da genel beklenen getiri M0’ın hala 0'a eşit olduğu anlamına gelir. Daha fazla düşünürsek, bu tür sonlu strateji kümelerinin sonsuz bir kümesinin de sıfıra eşit olduğu ortaya çıkar, çünkü sonsuz sayıda sıfırın toplamı 0 ile sonuçlanır. Grid durumunda, lot büyüklüğü her yerde aynıdır, martingale durumunda ise farklıdır, ancak bu fark nihai beklenen getiriyi hiçbir şekilde etkilemez. Her iki strateji de kombinatorikle uğraşmadan bu genel denklem kullanılarak tanımlanabilir. Her şey oldukça basit ve anlaşılırdır.

Bu stratejiler bu denklem kullanılarak tanımlanabildiğinden, her strateji için geçerlidir. Bu, işlem hacimlerinin manipülasyonunu içeren tüm stratejilerin ve herhangi bir karmaşıklıktaki emir açma/kapama sistemlerinin, işlemlerin açıldığı ve kapatıldığı andaki yaklaşık hareket yönünü veya en azından bazı yardımcı piyasa parametrelerini bilmeden başarısız olmaya mahkum olduğu sonucunu doğurur. Doğru bir öngörü olmadan, tüm çabalarımız sadece zaman ve para kaybıdır.

Grid ve martingale nasıl doğru kullanılır?

Grid, belirli bir yönde yaklaşan piyasa hareketi hakkında bilgi sahibi olmanız veya böyle bir olayın olasılığının yüksek olması durumunda yararlı olabilirken, bir gap riski de vardır. Gap’ler ve grid’ler birbiriyle anlaşamazlar. Bunun nedeni, emirlerin belirli bir adımla yerleştirilmesidir ve bir sonraki tikin tüm emirleri geçip grid’in çok ötesinde görünmesi meydana gelebilir. Elbette bu nadir bir durumdur, ancak kaçınılmaz olarak sistem performansını düşürür. Grid büyüklüğü tahmin edilen harekete eşit veya biraz daha küçük olarak ayarlanmalıdır, hareketin yönünü bilmemiz gerekmez, sadece yaklaşık değerini bilmemiz gerekir. Aşağıda, başarılı bir trend algılama algoritması durumunda bakiye grafiğinin nasıl göründüğü gösterilmektedir:

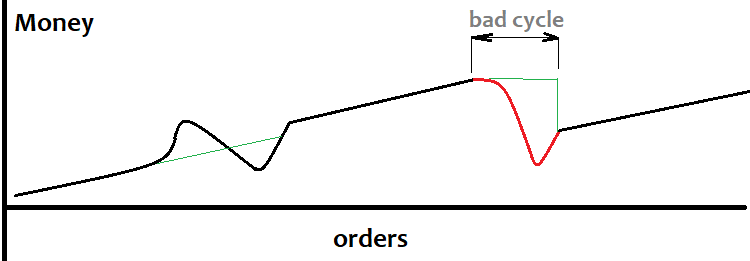
Bir trendi önceden tanımlamak her zaman mümkün değildir. Bu genellikle döngülerin kaybedilmesine yol açar (yukarıda kırmızı ile işaretlenmiştir) ve düşüş de oldukça büyüktür. Grid, büyük hareketleri tespit etme yöntemlerine sahip olanlar için faydalı olabilir. Bu durumda, grid özel sinyale dayalı olabilir. Bu konuyla henüz ilgilenmedim, bu nedenle güçlü hareketleri tespit etmek için iyi algoritmaları olan biri varsa, deneyiminizi paylaşmaktan çekinmeyin.

Şimdi martingale'i ele alalım. Beklenen getirisi "0" olan herhangi bir sinyalimiz varsa, ancak zararlar dizisinin, üst üste belirli sayıda zarar için kârlı bir işlem olasılığının bire yakın olacağı şekilde olduğu biliniyorsa, bu sinyal martingale için kullanılabilir. Bakiye grafiği şu şekilde görünür:

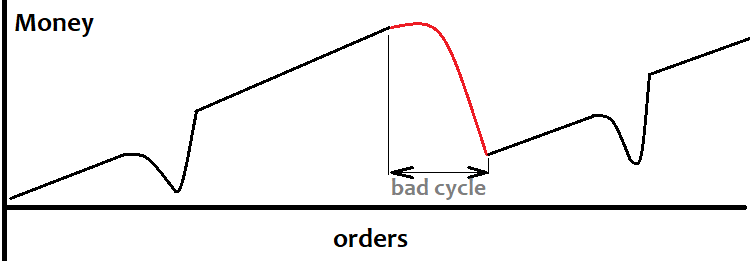
Ancak ben şahsen martingale'in her durumda tehlikeli olduğuna inanıyorum. Grid söz konusu olduğunda her şey daha kolay ve en önemlisi daha net görünse de, tarif ettiğim gibi koşulları elde etmenin neredeyse imkansız olduğuna inanıyorum.

Sonuç

Bu makalede, bu iki stratejiyi benzerliklerini, avantajlarını ve dezavantajlarını vurgulayarak olabildiğince açık bir şekilde anlatmaya çalıştım. Tüm açıklamaların yeni başlayanlar için bile anlaşılması kolay olduğuna inanıyorum. Makale çoğunlukla acemi yatırımcılara yöneliktir, ancak elde edilen sonuçlar, stratejilerin basit bir değerlendirmesinden ve uygulamalarının sınırlarından çok daha önemlidir. Burada sunulan genel matematiksel sonuçlar, herkesin kendi ticaret sistemlerini geliştirirken zamanlarını verimli bir şekilde kullanmalarına olanak tanıyacaktır. Makalenin kendisi piyasa fiziğini anlamaya yeni bir şey getirmemektedir, ancak birçok yatırımcının bu ilkeleri bilinçsizce kendi çıkarları için kullanmasını önleyebileceğini düşünüyorum.