MQL5 中的范畴论 (第 5 部分)：均衡器

概述

这是我们有关在 MQL5 中实现范畴论的系列文章的第五篇。 在上一篇文章中，我们探讨了如何利用跨度、实验和合成的概念来设置离场交易策略。 在本文中，我们将在上一篇文章中建立的基础上，探讨 MQL5 中均衡器的实现，从而改进有关离场交易的共享示例。 我们将探讨如何在范畴论中使用均衡器来比较和关联不同的态射，以及如何将其应用到交易策略，以便优化性能。 关于如何进一步利用这些思路来获得更准确的结果的可能指南将在最后分享。

均衡器

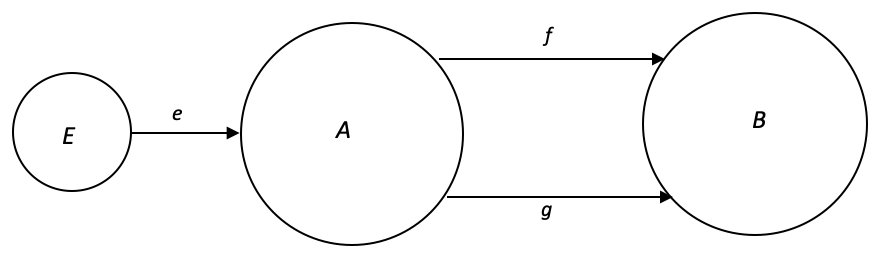
在范畴论中，均衡器被定义为范畴中的一个域，它表示两个域之间一对（或多个）平行态射的“共同行为”。 更准确地说，给定两个平行态射（f, g）：A --> B，f 和 g 的均衡器是满足以下条件的范畴中的域 E：

1. 存在一个态射 e：E --> A 使得 f . e = g . e。
2. 对于任何其它态射为 h 的域 X（上面未指出）：X --> A 如此 f . h = g . h，存在一个唯一的态射 u：X --> E 如此 h = e . u。

直观地说，均衡器是 A 的“最优大小”子域，它经由一对态射 f 和 g 映射 A 和 B，通过捕获 f 和 g 的“共同行为”，而只有映射到 B 中类似元素的 A 元素才包含在 E 中。这意味着任何其它域，类似于 E，通过 f 和 g 映射到 A 和 B，且能通过唯一的态射分解到 E（合成）。

等价关系确实满足三个性质中的至少一个；反身性、对称性和传递性。 这些定义充当等价的分类器。 他们尝试回答这些问题。 域是以哪种方式达到等价的？ 或者如何描述它们的关系？ 我们尝试从交易者的角度来描绘它们。 （符号 x R y 表示 x 与 y 的关系）。

1.     集合 A 上的关系 R 是自反的，当且仅当对于 A 中的每个 a 元素，a R a，即每个元素都与自身相关。

例如:

• 波动率微笑在外汇交易中呈现出一种反身等价关系，因为它围绕平价（at-the-money - ATM）执行价格是对称的，该价格等于货币对的远期汇率。 例如，如果 USD/EUR 货币对的 ATM 执行价格为 1.10，则波动率微笑在 1.10 执行价格附近对称。 故此，我们有执行价格 R 现货价格。
• 对于反身关系，并无很多有意义的例子可以分享，但我们可以看的一个明显的例子是汇率。 每种货币都通过其汇率与自身相关，汇率始终等于 1。 例如，美元兑美元的汇率始终为 1。 这意味着美元汇率 R 美元汇率。 

2.     集合 A 上的关系 R 是对称的，当且仅当对于每对元素，A 中的 a 和 b，如果 a R b，则 b R a。 换言之，如果 a 与 b 相关，则 b 与 a 相关。

绘述：:

• 如果两个货币对代表相同的汇率，但方向相反，则它们对称等价。 举例，EUR/USD 和 USD/EUR 对称等价，因为两者都代表欧元和美元之间的汇率，但一个以欧元报价，而另一个则以美元报价。 所以此处我们得到 EUR/USD R USD/EUR。
• 多头和空头持仓是对称等效的概念。 多头持仓涉及买入一种货币，预期其价值会上涨；而空头持仓涉及卖出一种货币，预期其价值会下跌。 这两笔持仓对称等价，因为它们代表了针对同一货币汇率的相反观点。

3.     集合 A 上的关系 R 是可传递的，当且仅当对于 A 中的每个三重元素：a、b 和 c，如果 a R b 和 b R c，则 a R c。 不同的说法就是，如果 a 与 b相关，且 b 与 c相关，则 a 与 c 传递相关。

演示:

• yi在外汇交易中，利率对等是一种理论，表明两种货币之间的汇率应该反映两国之间的利率差异。 如果货币 A 的利率高于货币 B，而货币 B 的利率高于货币 C，那么货币 A 的利率应该高于货币 C。这是传递等价的一个例子。
• 在外汇交易中，斐波那契（Fibonacci）交易涉及运用数学比率来判定货币价格的潜在支撑位和阻力位。 如果一个货币对回撤到其前一走势的 38.2%，然后又回撤到该回撤位的 50%，那么该货币对可能会继续回撤至 61.8% 的水平。 这是传递等价的一个例子。

均衡器具有开创性，因为它们为分析和优化复杂系统提供了强大的工具。 它们允许比较不同的证券、交易策略和投资组合，并可用于确保符合监管要求。 在证券交易中使用均衡器可以改变行业的交易，令交易者和投资者能够做出更明智的决策，并更有效地管控风险。

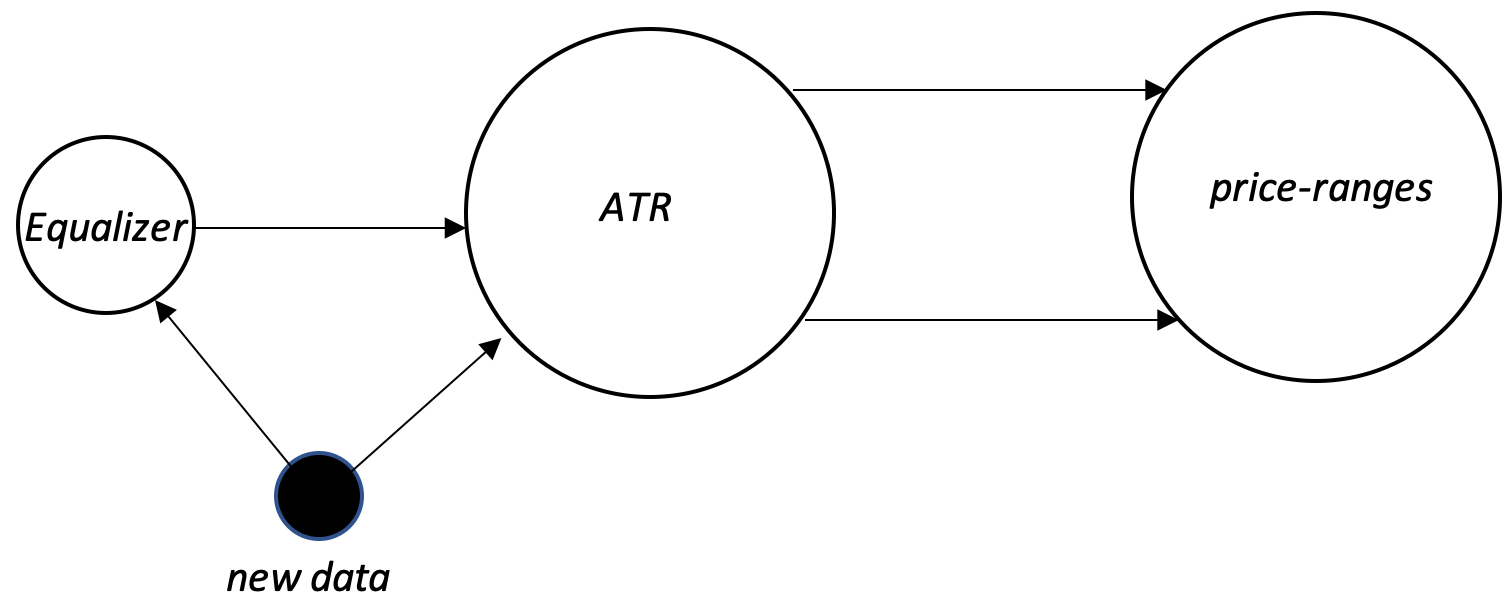
至于我们的文章，最简单的演示就是一个进行预测的指标。 根据我们上面的定义，我们得到的不是一个而是两个态射。 第一个我们可以称之为我们的假设，第二个测试结果。 我们选用 ATR 作为我们的指标，并预测价格范围变化。 这意味着我们的域 A 将是 ATR 值（我们可以将其常规化为 ATR 的变化），而协域将是价格柱线最高价减最低低的变化。

该假设是两个变体中的第一个，根据对指标操作的理论和学术理解，简单地将指标值映射到它们的参照物。 在我们的案例中，由于我们正在使用 ATR，并且我们希望它对范围的变化做出预测，我们的假设可能是这样的，“ATR 的负变化会变成柱线范围的负变化，相反，ATR 的正变化会演变为价格范围的正变化”。 如您所见，这是同构的。

ATR 变化和价格范围变化的值通常以点数为单位，这意味着它们需要常规化。 如果我们使用百分比，那么渐变就变得更容易了，因为 ATR 下降 20%，可以很容易地渐变为价格区间下降 20%。 如果为简洁起见，我们基于最后一根柱线指标值获得这些百分比，其中：

其中

            Dv 作为域值

            An 新的 ATR

            Ao 旧的 ATR

            Ao’ 旧 ATR 和点数*之间的最大值

            Cv 协域值

            Rn 新的价格范围

            Ro 旧价格范围

            Ro’ 旧价格范围和点数*之间的最大值，

 *最大值比较只是避免了零除法。

我们的公式将如上所述。 然而，即使采取了必要的步骤，我们仍然需要通过将百分比按百分位数分组或波段，来进一步常规这两个域。 故此，举例，下表展示了我们将在本例中可能采用的设置，从而达成此目的。

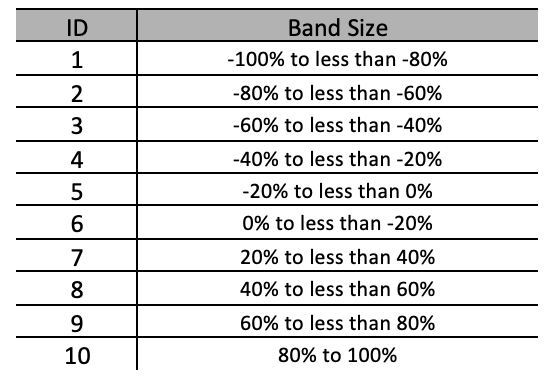
我们将有 10 个波段，每个波段的宽度约为 20%。 现在，这意味着我们可以更清晰地将域的元素映射到协域。 如此，举例，与其试图处理可能包含 12.7%、28.5%、-74.8% 等值的域数据，不如采用具有类似浮点数据的协域，我们现在于任一域中都有可以轻松配对的离散波带。

如此，为了形式化第一个态射，ATR 的假设变化与价格柱线范围的变化有一些滞后（在我们的例子中为一根柱线）正相关。 由于我们的两个域数据点是经过常规化的，它只是意味着我们的假设态射将是同构的，如上所述。 域中的 -100% 到 -80% 将映射到协域中的 -100% 到 -80%，同样，-80% 到 -60% 将映射到 -80% 到 -60%，依此类推。

对于第二个态射，我们将基于训练数据集上的样本计数进行映射。 故此，如果我们从 2021 年 01 月 01 日到 2022 年 01 月 01 日基于 EURGBP 进行测试，并且我们得出一个交叉表日志，记录了每个波段的 ATR 变化导致每个价格范围类似波段发生变化的次数。 这些测试基于 5 分钟的时间帧，且指标比较滞后单根柱线。 这意味着任何 ATR 指标读数都会与接下来的 5 分钟柱线价格范围变化进行比较。

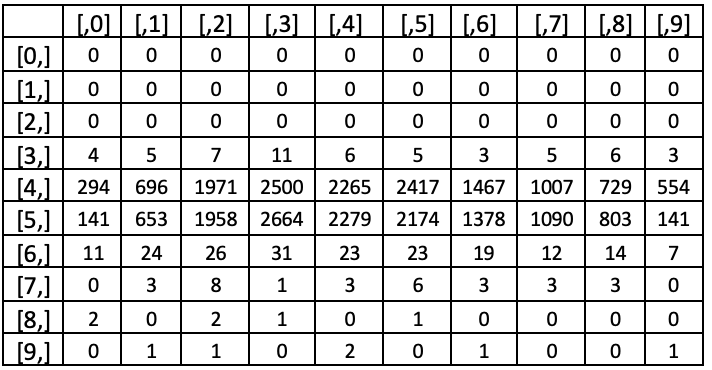
在我们的交叉表中，列标题 [,0],[,1] 等分别代表 -100% 到 -80% 以上波段大小的行，-80% 到 -60%，等等。 这些行也遵循类似的配对。 从测试结果来看，很明显大多数 ATR 百分比变化的幅度小于 20%。 这意味着运行更有意义的测试，可以在该范围内提供更多的分区（波带大小），而在超出该范围的范围中提供更少的分区（波带大小）。 所以，这意味着分布更“均匀”的样品的波带大小不会相同。 不过，如果我们坚持使用所选波段大小，我们将确定每行（在所有列中）的最高列值，这将指示它是相应 ATR 变化的最高概率价格范围变化。

因此，这就是我们的两个态射，它们的等价性能更好地描述对称。

假设的同态输出将记录如下：

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-100% to -80%)|----->(-100% to -80%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-80% to -60%)|----->(-80% to -60%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-60% to -40%)|----->(-60% to -40%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-40% to -20%)|----->(-40% to -20%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-20% to 0%)|----->(-20% to 0%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (0% to 20%)|----->(0% to 20%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (20% to 40%)|----->(20% to 40%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (40% to 60%)|----->(40% to 60%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (60% to 80%)|----->(60% to 80%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (80% to 100%)|----->(80% to 100%)

运行测试会记录以下内容：

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-100% to -80%)|----->(-100% to -80%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-80% to -60%)|----->(-100% to -80%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-60% to -40%)|----->(-100% to -80%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-40% to -20%)|----->(-40% to -20%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (-20% to 0%)|----->(-40% to -20%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (0% to 20%)|----->(-40% to -20%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (20% to 40%)|----->(-40% to -20%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (40% to 60%)|----->(-60% to -40%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (60% to 80%)|----->(-100% to -80%)

2023.03.31 17:55:58.318        ct_5 (EURUSD.ln,M5) (80% to 100%)|----->(-20% to 0%)

现在，基于这两个态射，我们可以在域内判定（ATR 的百分比变化）哪些百分比波段由两个态射与协域中的相同百分比带匹配（价格范围变化的百分比变化）。根据上面共享的定义，ATR 变化的这个子集将成为假设态射和测试运行态射的均衡器。 这些波段如下所示。

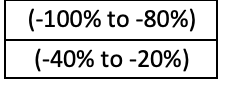
这两个态射的均衡器的主要应用将像上一篇文章一样，按照通用性质。 到目前为止，这两个态射是基于一个假设和历史数据。 在前瞻性数据上，它们不可能太可靠。 如此，在我们可以使用实时或前向数据的价格范围预测系统来做出决策之前，我们需要定义我们的锚点态射，也就是通用性质，根据定义，它将介于任何新数据点和我们的均衡器之间。 我们可以将这种通用性质态射定义为简单的包含检查，或者定义为复杂的线性甚至二次关系。

故此，如果我们首先考虑简单关系，这就是我们的系统在预测价格范围变化时处理新的 ATR 百分比变化数据的方式。 对于任何新的数据点（ATR 变化），我们会将其与我们的均衡器域进行比较，并判定它是否是该域的子集。 如果它是一个子集，则它与均衡器中相等区域之间的同构态射遵照通用性质规则推断。 这个均衡器又是我们 ATR 变化域的一个子集，假设和测试结果这两个态射源自价格柱线变化域中的“一致”。 据此，我们可以很容易地解读出这个新数据点预测的价格柱线变化。

如果我们的数据点不是均衡器的子集，这意味着不能依靠它来预测价格范围的变化，所以我们“什么都不做”，等待下一个指标数据点。

备案则是，我们可以让测试结果态射和通用性质态射都呈现出稍微复杂的关系，就像二次函数一样，它分别包含 ATR 变化和新数据作为指数。 这些变化必然会引导更准确的预测，但应注意避免过度拟合，测试应该在很长一段时间内进行，最好是针对您的经纪商的真实跳价数据。

结束语

总之，我们已经看到了如何运用范畴论中的均衡器来估算基于 ATR 指标的波动性变化。 通过使用均衡器，我们能够比较和关联不同的态射，并开发一种研究采样期间波动趋势的方法。

通过应用通用性质，我们能够从样本数据中提取见解，并对样本外数据的波动性变化进行估算。 这可能会导致更明智的交易决策，不仅在于此处所示的离场持仓，而且涵盖常见交易系统的其它方面。