MQL5 中的范畴论 (第 6 部分):单态回拉和满态外推
概述
在上一篇文章中,我们讨论了如何运用范畴论中的均衡器,基于抽样数据评估波动率变化。 在这篇跟进文章中,我们将通过探索各种锥体设置相对于最终分析结果的重要性,来深入研究范畴论中的合成和锥体。 我们并非在研究可预测或描述市场某些方面的的另一个范畴论概念,而是更具体地对范畴论合成和锥体进行敏感性分析。
在此之前,我们回顾一下上一篇文章概念的双重性,协均衡器。
协均衡器
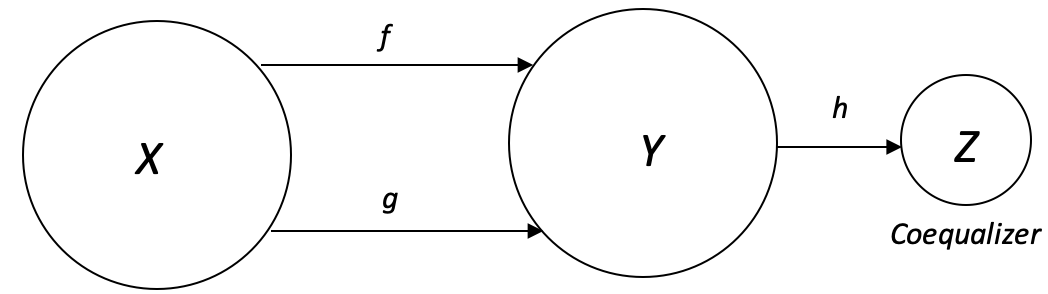
协均衡器,即上一篇文章中介绍的均衡器的对偶性,是从通常不同的共域中获取元素的域(回想一下,均衡器专注于相似的元素),并通过协均衡器态射,为每个域元素视差产生一个元素。 在新均衡器域中创建的公共元素是针对域中的每个元素所做的。 这通常绘制如下:
因此,函数 h 充当商值,因为对于域中的每个值 d,可以根据态射(无论是 f 还是 g)映射到不同的值,协均衡器域中的最终结果(元素)是相同的。
一个值数组乘以 “公共值分子 Z” 除以相同的值数组将始终产生公共值。 如此,除以 Y 中的值数组就像 Y 的商。这通常表示为:
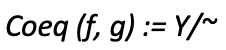
依据 h,商函数定义为
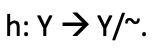
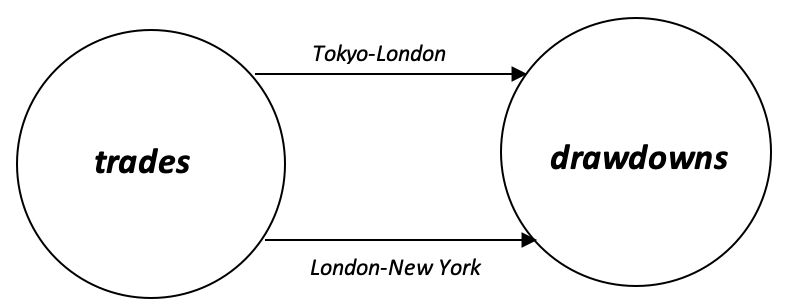
如此,在实践中,对于交易者来说,如果我们有以下来自最近交易活动的日志;
我们可以推断出以下示图:
依据这张示图,我们可以选择提出一个协均衡器,基于我们是在交易东京-伦敦重叠,亦或伦敦-纽约重叠,来指导我们的持仓规模。 如果我们根据记录的回撤针对仓位规模进行逆向加权,我们将得到一个基于更坏情况的协均衡器等价物。 这可在无需范畴论的情况下完成。 范畴论会有所帮助的地方是应用通用性质。 这在前两篇文章中已经强调过。 在我们的例子中,我们可以将实时回撤读数与我们加权投资组合的加权(最坏情况)值进行比较。 如果当前值比我们预期的差,那么我们将针对持仓规模进行适当的更改。
单态回拉
单态性是一种单射同态,其基数域小于或等于共域,从域的所有态射映射到共域中的不同元素。 范畴论中的回拉是锥体中的一个域(又名纤维乘积),在典型的 4 域锥体中,它与乘积域对角线相对。
将这两个概念放在一起会产生一个有趣的性质。 如果我们参考下图:
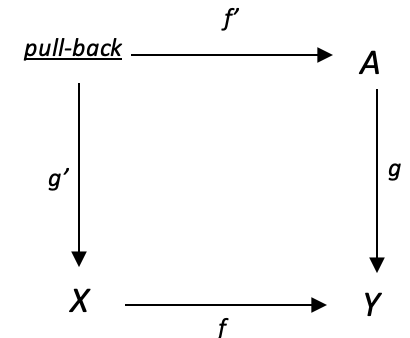
如果 g:A --> Y 是单态,那么对于任何函数 f:X --> Y,图中的左映射 g':回拉 --> X 也是单态,前提是有代偿。
为了描绘这一点,我们考虑一个包含乘积域 Y、因子域 X、因子域 A,和回拉域的锥体;最近 N 根柱线的 EURJPY,EURUSD,USDJPY,和 USDX(美元指数)分别与前 N 根柱线相关值。
N 的值可以从遵循斐波那契数列的分位数桶中选择。 在我们的例子中,我们将选用五个值,即 3,5,8,13, 和 21。 故此,每个域都将拥有这些周期当中每一个的相关性。 这些值确实会不时更改,这就是为什么本体日志有助于每次记录所有这些值的原因。 故此,本体日志将为每个周期提供一个圆锥体。
我们不会在本文中使用本体日志,但是我们将在周线时间帧内计算和呈现 6 个月内各种锥体值的测试日志。
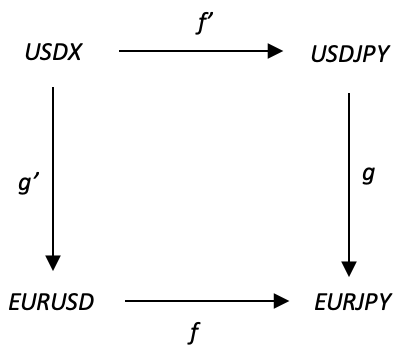
不过,为了继续上面的图表,每个域都包含跨周期 3、5、8、13 和 21 的相关性,同态 f、g、f' 和 g' 将简单地将这些同态配对到这些周期的域中。 因此,USDX 最近 5 周和之前的 5 周之间的相关性(在 f' 下)将与 USDJPY 最近 5 周和之前的 5 周之间的相关性配对,依此类推。
乘积域 EURJPY 还将包含上述 5 个周期的相关值,但其值将是域 EURUSD 和 USDJPY 之间乘积的结果。 这两个域的乘积则是两个域的几何平均值。 现在,几何平均值通常是两个乘积的平方根。 在我们的例子中,这些乘积将是两个相关性。 因为这些相关性可能是负的,我们不会深入研究虚数,所以谨慎的做法是将相关值常规化,令其范围从 0.0 到 2.0,而不是 -1.0 到 1.0。 一旦获得平方根/几何值后,我们可以恢复为 -1.0 到 1.0 的标准格式。
故此,为了常规化,我们将在计算几何平均值之前将相关值加 1.0。 一旦我们有了平均值,我们只需减去 1.0 即可恢复到标准。
如果出于控制目的,我们首先使用我们的锥体运行测试,其不用该性质,而只是使用上面的周期长度分位数桶,从 2021-07-01 到 2022-01-01(约 26 周)在周线时间帧内,同时仅选择 USDX 中相关性最高的周期,这些将是我们的结果:
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [,0] [,1] [,2] [,3] [,4] [,5] 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 0,] " DATE " ," N period " ," EURUSD corr. " ," USDJPY corr. " ," geometric mean "," actual corr. " 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 1,] "2021.07.04 00:00","13" ,"0.49" ,"0.90" ,"0.69" ,"0.25" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 2,] "2021.07.11 00:00","5" ,"0.70" ,"0.00" ,"0.30" ,"-0.00" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 3,] "2021.07.18 00:00","5" ,"0.70" ,"0.10" ,"0.37" ,"0.20" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 4,] "2021.07.25 00:00","5" ,"0.50" ,"-0.20" ,"0.10" ,"0.70" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 5,] "2021.08.01 00:00","5" ,"0.80" ,"0.10" ,"0.41" ,"0.50" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 6,] "2021.08.08 00:00","5" ,"0.80" ,"0.30" ,"0.53" ,"0.20" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 7,] "2021.08.15 00:00","5" ,"0.90" ,"0.30" ,"0.57" ,"0.70" 2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1) [ 8,] "2021.08.22 00:00","5" ,"0.40" ,"0.50" ,"0.45" ,"0.90" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 9,] "2021.08.29 00:00","5" ,"0.20" ,"0.70" ,"0.43" ,"0.50" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [10,] "2021.09.05 00:00","5" ,"-0.20" ,"0.60" ,"0.13" ,"0.00" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [11,] "2021.09.12 00:00","21" ,"0.69" ,"0.27" ,"0.46" ,"-0.79" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [12,] "2021.09.19 00:00","5" ,"0.60" ,"-0.20" ,"0.13" ,"0.50" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [13,] "2021.09.26 00:00","5" ,"0.30" ,"0.20" ,"0.25" ,"0.60" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [14,] "2021.10.03 00:00","3" ,"1.00" ,"1.00" ,"1.00" ,"-0.50" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [15,] "2021.10.10 00:00","13" ,"0.55" ,"0.49" ,"0.52" ,"-0.29" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [16,] "2021.10.17 00:00","13" ,"0.60" ,"0.65" ,"0.62" ,"-0.36" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [17,] "2021.10.24 00:00","13" ,"0.62" ,"0.51" ,"0.56" ,"-0.45" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [18,] "2021.10.31 00:00","13" ,"0.64" ,"0.53" ,"0.59" ,"-0.55" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [19,] "2021.11.07 00:00","5" ,"0.80" ,"-0.50" ,"-0.05" ,"-0.10" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [20,] "2021.11.14 00:00","5" ,"0.50" ,"0.50" ,"0.50" ,"-0.70" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [21,] "2021.11.21 00:00","3" ,"1.00" ,"1.00" ,"1.00" ,"1.00" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [22,] "2021.11.28 00:00","3" ,"0.50" ,"0.50" ,"0.50" ,"1.00" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [23,] "2021.12.05 00:00","8" ,"0.76" ,"-0.62" ,"-0.18" ,"-0.02" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [24,] "2021.12.12 00:00","8" ,"0.62" ,"-0.52" ,"-0.12" ,"-0.12" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [25,] "2021.12.19 00:00","8" ,"0.40" ,"-0.05" ,"0.16" ,"-0.26" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [26,] "2021.12.26 00:00","3" ,"0.50" ,"0.50" ,"0.50" ,"0.50"
在这些结果中,几何平均值和实际值之间的相关性为 -0.07,这意味着我们从 USDX 中选择最高相关周期的设想并不能准确预测 EURJPY 的值。
如果我们继续查看上面的单态性质,实现将意味着域将不会得到相同的基数。 我们最初根据斐波那契级数的一部分选择了一组周期,包括 3、5、8、13 和 21。 从上面的测试运行日志中,选择了与美元指数(USDX)相关性最高的日志。 例如,在 2021 年 09 月 05 日,选择 5 周期意味着当前 5 根 USDX 柱线与前 5 根柱线的相关性是所有周期 3、5、8、13 和 21 中最高的,因此选中它,并用作 EURUSD 和 USDJPY 的相关周期。
不过,如果我们确实将单态性质应用于 USDJPY 趋向 EURJPY 和 USDX 趋向 EURUSD 平行边上的锥体,我们可以得到更有趣的结果。 为了达成这一点,我们将重点关注域的基数。 我们的锥体由 USDX 趋向 EURJPY 组成,由于单态与域相比需要相等或更大的共域,因此我们可以通过将域规模从 USDX 趋向 EURJPY 轻松确保每个同态都是单射的,并避免任何态射指向共域中的相同元素。
我们扩展域规模的单位是我们分配给每个域的周期长度的分位数桶。 故此,我们需要像上一篇文章中尝试的那样为每个域提供分位数桶。 因此,将其与我们的锥体流程放在一起意味着域 USDX 将具有最少的存储桶,但随着我们往 EURJPY 迈进,每个域的分位数存储桶数量将增加。
为了特别匹配我们上面的单态性质,我们将有如上所述 |USDX| = 5,但我们将有 |EURUSD| = 19,|USDJPY| = 5,和 |EURJPY| = 19。 因此,周期不会根据上面使用的斐波那契数列进行分桶,但对于域,USDJPY 和 EURJPY 将在 3 到 21 的范围内单独使用。 因此,态射 g 和 g',我们的单态,将使用另一个指标来帮助从较小规模的域映射到较大规模的域。
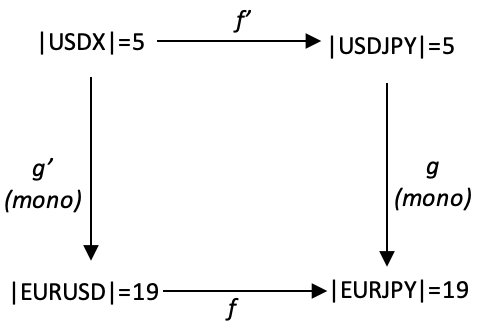
我们映射态射 g' 和 g 所用的指标是 RSI。 由于 RSI 是循环的,并且很容易从 0-100 归一化,因此它是合适的。 您可以选择类似的不同指标,但在我们的例子中,指标读数将决定共域的相关比例。 极端值 3 和 21 将保持原样不变,但值 5 将与 RSI 读数成正比映射到 4、5、6 或 7。
运行与上述类似的测试,在 USDX 中采用相同的周期选择准则,为我们提供这些日志。
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [,0] [,1] [,2] [,3] [,4] [,5] 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 0,] " DATE " ," N period " ," EURUSD corr. " ," USDJPY corr. " ," geometric mean "," actual corr. " 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 1,] "2021.07.04 00:00","13" ,"0.13" ,"0.90" ,"0.47" ,"0.24" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 2,] "2021.07.11 00:00","5" ,"-0.49" ,"0.00" ,"-0.28" ,"-0.49" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 3,] "2021.07.18 00:00","5" ,"0.37" ,"0.10" ,"0.23" ,"-0.09" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 4,] "2021.07.25 00:00","5" ,"0.20" ,"-0.20" ,"-0.02" ,"-0.09" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 5,] "2021.08.01 00:00","5" ,"0.43" ,"0.10" ,"0.25" ,"0.14" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 6,] "2021.08.08 00:00","5" ,"0.26" ,"0.30" ,"0.28" ,"0.37" 2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1) [ 7,] "2021.08.15 00:00","5" ,"-0.20" ,"0.30" ,"0.02" ,"0.09" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [ 8,] "2021.08.22 00:00","5" ,"-0.71" ,"0.50" ,"-0.35" ,"0.14" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [ 9,] "2021.08.29 00:00","5" ,"-0.89" ,"0.70" ,"-0.56" ,"-0.31" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [10,] "2021.09.05 00:00","5" ,"-0.77" ,"0.60" ,"-0.40" ,"-0.31" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [11,] "2021.09.12 00:00","21" ,"0.68" ,"0.27" ,"0.46" ,"-0.88" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [12,] "2021.09.19 00:00","5" ,"-0.31" ,"-0.20" ,"-0.26" ,"-0.09" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [13,] "2021.09.26 00:00","5" ,"0.54" ,"0.20" ,"0.36" ,"0.77" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [14,] "2021.10.03 00:00","3" ,"-0.80" ,"1.00" ,"-0.37" ,"-0.20" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [15,] "2021.10.10 00:00","13" ,"0.16" ,"0.49" ,"0.32" ,"-0.42" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [16,] "2021.10.17 00:00","13" ,"0.43" ,"0.65" ,"0.53" ,"-0.47" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [17,] "2021.10.24 00:00","13" ,"0.68" ,"0.51" ,"0.59" ,"-0.53" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [18,] "2021.10.31 00:00","13" ,"0.78" ,"0.53" ,"0.65" ,"-0.58" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [19,] "2021.11.07 00:00","5" ,"0.89" ,"-0.50" ,"-0.03" ,"0.71" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [20,] "2021.11.14 00:00","5" ,"0.89" ,"0.50" ,"0.68" ,"0.37" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [21,] "2021.11.21 00:00","3" ,"-0.40" ,"1.00" ,"0.10" ,"-0.20" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [22,] "2021.11.28 00:00","3" ,"-0.40" ,"0.50" ,"-0.05" ,"1.00" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [23,] "2021.12.05 00:00","8" ,"0.33" ,"-0.62" ,"-0.29" ,"-0.12" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [24,] "2021.12.12 00:00","8" ,"0.43" ,"-0.52" ,"-0.17" ,"-0.23" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [25,] "2021.12.19 00:00","8" ,"0.60" ,"-0.05" ,"0.23" ,"0.10" 2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1) [26,] "2021.12.26 00:00","3" ,"0.40" ,"0.50" ,"0.45" ,"-0.80"
两个结果集之间没有明显的统计差异。 而这次的结果 -0.08 同样增加了近 15%。 域的锥体和链接,以及它们的各种元素(在这种情况下是相关性)确实为研究形态和趋势提供了机会,这些心态和趋势本身并不明显,但在交易中却非常确定。
满态外推
满态是一种满射同态,其域的基数比共域大,并且从域映射到共域中所有元素的态射意味着没有一个是未链接的。 范畴论中的外推是锥体中的一个域(又名纤维共积),在典型的 4 域锥体中,它与共积域对角线相对。
像我们对单态回拉所做的那样,将这两者放在一起,也给了我们一个性质。 如下图所示:
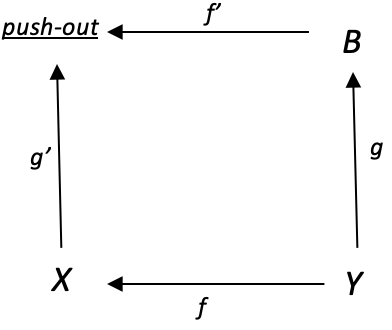
如果 g:Y --> B 是满态,那么对于任何函数 f:Y --> X,图中左边映射 g':X --> 外推也是一个满态。 为了探索这一点,我们再次参考一个锥体,其共积域 Y 是任何证券买入价的布林线范围值。 两个共积因子域(X 和 B)将是布林带上、下包络线。 这两者之间的差值(或“共积联合”)将为我们提供对布林线范围的预测。 推出域将是布林带的基线移动平均线,据其得出上、下包络线。
就像我们使用周期长度作为变量,在上面的单态回调中提出各种相关系数一样,我们将再次采用周期长度为每个域推导各种移动平均值,从而为我们提供各种各样的布林包络线。 如上所述,对于我们的探索性测试,我们可以从周期 3、5、8、13 和 21 开始。
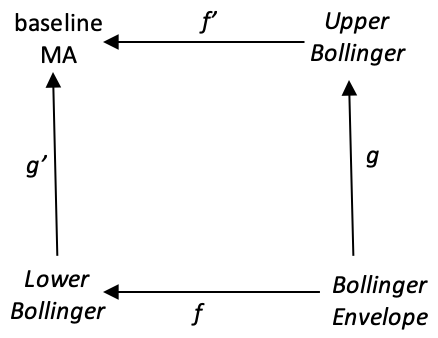
如此,我们的锥体由布林包络线域趋至基线 MA 域组成。 它的组成方向与我们单态推出的第一个锥体相反,因为它的顶点是共积,而不是像以前那样的乘积。 态射箭头显示同态方向。 每个域中元素的链接将简单地遵循我们上面所说的各自的 N 周期。
因此,如果我们运行测试,在应用满态性质之前,通过根据最小标准偏差在基线 MA 域选择周期,我们将得到以下日志:
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [,0] [,1] [,2] [,3] [,4] [,5] [,6] 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 0,] " DATE " ," N period " ," Baseline-MA " ," Upper Bands " ," Lower Bands " ," Envelope Delta "," Actual Range " 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 1,] "2021.07.04 00:00","8" ,"103.425" ,"105.548" ,"101.301" ,"4.248" ,"0.850" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 2,] "2021.07.11 00:00","8" ,"103.425" ,"105.548" ,"101.301" ,"4.248" ,"0.758" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 3,] "2021.07.18 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"0.691" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 4,] "2021.07.25 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"1.193" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 5,] "2021.08.01 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"1.030" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 6,] "2021.08.08 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"0.735" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 7,] "2021.08.15 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.270" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 8,] "2021.08.22 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.868" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [ 9,] "2021.08.29 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.854" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [10,] "2021.09.05 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.750" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [11,] "2021.09.12 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.912" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [12,] "2021.09.19 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.565" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [13,] "2021.09.26 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.325" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [14,] "2021.10.03 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.770" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [15,] "2021.10.10 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.811" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [16,] "2021.10.17 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.700" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [17,] "2021.10.24 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.035" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [18,] "2021.10.31 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.842" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [19,] "2021.11.07 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.400" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [20,] "2021.11.14 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"1.305" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [21,] "2021.11.21 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"0.933" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [22,] "2021.11.28 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.115" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [23,] "2021.12.05 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.747" 2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1) [24,] "2021.12.12 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.077" 2023.04.07 19:04:11.242 ct_6 (USDX-JUN23,W1) [25,] "2021.12.19 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.685" 2023.04.07 19:04:11.242 ct_6 (USDX-JUN23,W1) [26,] "2021.12.26 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.778"
我们在分析与实际之间的相关性检查处在 0.12,这仍旧不太明显。
这就把我们带到了满态性质。 如果我们将其应用于锥体的平行两侧,就是说 “下布林线 --> 基线 MA 和布林线包络线 --> 上布林线”,我们可能会得到不同的结果。 为了达成这一点,我们将再次关注域的基数。 我们的锥体由来自布林包络线的基线 MA 组成,因为它是共积,而不是先前的乘积。 由于与共域相比,满态需要相等或更大的域,因此我们可以通过将共域规模从布林包络增加到基线 MA 来轻松确保每个同态都是满射的,并确保每个相应的共域中的所有元素都映射到它。
如上所述,由于我们应用了基于斐波那契的分位数桶,我们可以简单地明确我们希望更大的域。 如上所述,这意味着我们的基数将是 | LOWER-BOLLINGER| = 19 且 | BOLLINGER-ENVELOPE | = 19。 较大的域保持在顶点和较低因子域,因为给定共积的组成是相反的。
采用这些设置运行测试,为我们提供了以下结果:
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [,0] [,1] [,2] [,3] [,4] [,5] [,6] 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 0,] " DATE " ," N period " ," Baseline-MA " ," Upper Bands " ," Lower Bands " ," Envelope Delta "," Actual Range " 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 1,] "2021.07.04 00:00","8" ,"103.425" ,"105.548" ,"101.301" ,"4.248" ,"0.850" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 2,] "2021.07.11 00:00","8" ,"103.425" ,"105.548" ,"101.301" ,"4.248" ,"0.758" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 3,] "2021.07.18 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"0.691" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 4,] "2021.07.25 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"1.193" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 5,] "2021.08.01 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"1.030" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 6,] "2021.08.08 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"0.735" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 7,] "2021.08.15 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.270" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 8,] "2021.08.22 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.868" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [ 9,] "2021.08.29 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.854" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [10,] "2021.09.05 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.750" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [11,] "2021.09.12 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.912" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [12,] "2021.09.19 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.565" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [13,] "2021.09.26 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.325" 2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1) [14,] "2021.10.03 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.770" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [15,] "2021.10.10 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.811" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [16,] "2021.10.17 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.700" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [17,] "2021.10.24 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.035" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [18,] "2021.10.31 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.842" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [19,] "2021.11.07 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.400" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [20,] "2021.11.14 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"1.305" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [21,] "2021.11.21 00:00","13" ,"102.993" ,"105.163" ,"100.822" ,"4.341" ,"0.933" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [22,] "2021.11.28 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.115" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [23,] "2021.12.05 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.747" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [24,] "2021.12.12 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"1.077" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [25,] "2021.12.19 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.685" 2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1) [26,] "2021.12.26 00:00","21" ,"103.616" ,"106.326" ,"100.906" ,"5.420" ,"0.778"
再一次,结果与 0.16 不同,这意味着变化超过 30%。
结束语
总之,我们已经看到由其域组成的锥体,如何通过观察指标和时间序列的方式将其联系起来并进行分析,而这些并不总是显而易见的。 范畴论中的锥体在配对域中提出了许多排列,这本身就导致了多种观察、解释和预测的方式。 具体来说,在本文中,我们已经看到了如何通过应用单态回拉和满态推出对锥体组成进行轻微的限制性调整,可以将最终结果改变 15 - 30%。 通过应用权重和其它变化来观察态射,不仅可以开发新颖的入场信号,还可以开发成熟的资金管理系统。 通过本文附带的脚本文件,读者可以根据自己的特定指标和交易风格对其进行微调。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/12437
 付款和付款方式
付款和付款方式
 MQL5.community - 用户手册
MQL5.community - 用户手册