Teoría de Categorías en MQL5 (Parte 10): Grupos monoidales
Introducción
En el artículo anterior, continuamos nuestro análisis de los monoides tomando la acción de monoides como un medio para transformar conjuntos de monoides ampliando sus posibles elementos. Hasta ahora en general hemos considerado los conceptos: dominios, morfismos y axiomas de categorías, incluyendo los productos fibrados monomorfos y los coproductos fibrados epimórficos. Mientras que algunos podrían argumentar que la realización de los conceptos de la teoría de categorías requiere una exploración más amplia de todos o la mayoría de sus conceptos, el enfoque adoptado aquí consiste en analizar qué ideas podrían resultar útiles desde el punto de vista de una visión básica o limitada del tema. Cada uno de estos artículos (aunque en algunos casos los conceptos se han tomado prestados de artículos anteriores) ha demostrado la capacidad de simplificar la vida de los tráders y, en algunos casos, de mejorar los sistemas comerciales. En el presente artículo, veremos los monoides en grupos. Al igual que las acciones de monoides tratadas en el artículo anterior, se verán como una redefinición del monoide en el momento de la decisión de la transacción. Recordemos que las acciones de monoides se consideraban extensiones del conjunto de monoides. Aquí sobreestimaremos otro parámetro del monoide, a saber, el elemento de identidad, ya que una vez más redefiniremos nuestros monoides. Dentro del alcance de este artículo no se encuentra la construcción de sistemas comerciales completos, como sucedió en algunos artículos anteriores, donde creamos ejemplares de clase de señal y/o asesores de seguimiento con el fin de construir asesores completos con el Wizard MQL5 incorporado. En su lugar, examinaremos las funciones individuales que forman parte de nuestras clases codificadas, acciones y grupos de monoides, y analizaremos cómo pueden ser útiles para el tráder en puntos de decisión clave.
Comprendiendo los grupos de monoides
Como recordará, los monoides son conjuntos, elementos iguales que pertenecen a esos conjuntos y operaciones binarias que utilizan dos elementos cualesquiera del conjunto y siempre devuelven un elemento que es miembro del conjunto. Además, si algún miembro de un conjunto está asociado a un elemento igual en una operación binaria, el resultado será siempre ese elemento. Las acciones de monoides de las que hablamos en nuestro último artículo, son una forma de función definida por un conjunto y una operación binaria que asocia elementos de un conjunto de monoides con el conjunto de esa función y siempre da como salida un elemento que es miembro del conjunto de la función. Los consideramos como un medio de transformación de monoides porque la salida de la operación monoidal binaria era cerrada, ya que todos los resultados eran estrictamente miembros del conjunto de monoides.
Sin embargo, convendría empezar señalando que no existen diferencias entre los grupos y los grupos monoidales. La única diferencia es que nosotros nos referimos estrictamente a conjuntos (o dominios) pertenecientes a una categoría. Así, un grupo monoide, partiendo de la definición de grupo, es un monoide con la propiedad adicional de que cada elemento del conjunto de monoides debe tener un elemento inverso. Cuando un elemento y su inversión se emparejan en una operación monoidal binaria, el resultado será siempre el elemento equivalente del monoide.
Formalmente la propiedad inversa que distingue al grupo de monoides
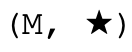
de los monoides habituales para cada
![]()
existe también un elemento inverso
![]()
del tipo que:
![]()
donde e es el elemento de identidad del monoide.
La aplicación para tráders se tratará de la misma forma que en el artículo anterior. Como recordará, estamos analizando los monoides (conjuntos) como un conjunto de opciones de decisión entre las que puede elegir un tráder. En el artículo anterior, consideramos la posibilidad de aumentar el tamaño de este conjunto usando acciones de monoides o monoidales. Asimismo, investigamos qué impacto tendría esto en el rendimiento del sistema comercial si ampliáramos el alcance de monoides específicos basándonos en una lista de factores que ponderan la importancia relativa de los puntos de decisión (parámetros) del sistema comercial. Los resultados fueron inferiores a la media en comparación con los obtenidos en el artículo que consideraba los monoides restringidos (por defecto). En el caso de los grupos monoidales, en lugar de ampliar el ámbito de nuestros conjuntos de monoides, volveremos a los monoides restringidos que tenían una acción y se transformaron en grupos. Así, consideraremos el cambio de la composición de los conjuntos tras la acción de dicho monoide, pero la implementación real del sistema comercial no se analizará en este artículo. Le sugiero que estudie este tema por su cuenta.Implementación de grupos monoidales en MQL5
Al configurar nuestro entorno de MQL5 para implementar grupos monoidales, lanzaremos la IDE y crearemos un nuevo archivo script usando el wizard.
Nombremos nuestro script ct_10 en la pestaña contigua y clicaremos en Finish. El script hará referencia al archivo de clase ct_10.mqh, que es una modificación de la clase ct_9.mqh de la que hablamos en el artículo anterior. Para una panorámica más completa, podría ser útil repasar los pasos de creación de la clase monoidal que formaba parte de ct_9.mqh, que mencionamos en los dos artículos anteriores. Como recordaremos, nuestra unidad de construcción básica es una clase de elementos, que es básicamente un array de objetos de tipo de datos T. El tipo de datos T se establece al inicializar el elemento.
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ template <typename T> class CElement : public CObject { protected: int cardinal; T element[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
La clase de elementos, a su vez, es llamada por el conjunto (clase de dominio) como un array.
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ template <typename T> class CDomain : public CObject { protected: int cardinal; CElement<T> elements[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
Hemos ido un poco más allá y hemos definido no solo una clase de categorías que definan formalmente los grupos monoidales como distintos de los grupos, sino también las clases de morfismos, homomorfismos y otra serie de nociones. Dado que (al igual que sucede en la clase de categorías) no tienen por sí mismas importancia crítica para la construcción de una clase monoidal, no las enumeraremos ni las consideraremos en este artículo. Sabemos que un monoide es un conjunto, un elemento de identidad y una operación binaria. Si tuviéramos que definir una operación binaria, podríamos hacerlo enumerando nuestros parámetros en forma de enumeración. En los dos últimos artículos, hemos usado algo parecido a esto.
//+------------------------------------------------------------------+ //| Enumeration for Monoid Operations | //+------------------------------------------------------------------+ enum EOperations { OP_FURTHEST=5, OP_CLOSEST=4, OP_MOST=3, OP_LEAST=2, OP_MULTIPLY=1, OP_ADD=0 };
No vamos a revisar el código de nuestro artículo. Baste decir que establece los medios que permiten personalizar y definir las operaciones binarias para los elementos correspondientes de un conjunto de monoides. Las posibilidades aquí son interesantes. Pasando a la clase monoidal, vamos a crear nuestra clase como heredada públicamente de la clase de dominio en lugar de definir una nueva clase con un ejemplar del conjunto (dominio). Este es un código eficiente que muestra intuitivamente que un monoide es simplemente un dominio con una operación binaria y un elemento de identidad unido a él.
//+------------------------------------------------------------------+ //| Monoid Class | //+------------------------------------------------------------------+ template <typename T> class CMonoid : public CDomain<T> { protected: //double weights[]; int identity; EOperations operation; public: double weights[]; ... void Operation(EOperations Value) { operation=Value; } EOperations Operation() { return(operation); } ... CMonoid(){ identity=0; operation=OP_ADD; }; ~CMonoid(){}; };
A esta clase añadiremos dos axiomas adicionales de operación binaria y un elemento de identidad. Nuestro elemento igual, sin embargo, no será otro ejemplar del elemento. Ya está en el array de elementos de dominio. En su lugar, simplemente haremos referencia al índice de este array que apunta a nuestro elemento de identidad. La clase monoidal se puede inicializar con un puntero automático en nuestro script, como se muestra en el siguiente ejemplo.
La clase de acciones monoidales descrita en el artículo anterior se heredará de esta clase monoidal.
No obstante, para los grupos monoidales, no hay semánticamente ninguna diferencia en el código de la clase entre un monoide y un grupo monoidal. Solo podremos comprobar el requisito de inversión con los grupos monoidales. Por lo tanto, para nuestro objetivo, la clase de grupo monoidal tendrá una función de comprobación HasInversion como se muestra a continuación.
//+------------------------------------------------------------------+ //| Monoid Group Class | //+------------------------------------------------------------------+ template <typename T> class CMonoidGroup : public CMonoid<T> { protected: public: bool HasInversion() { bool _has_inversion=true; for(int i=0;i<this.Cardinality();i++) { bool _has_inverse=false; for(int ii=0;ii<this.Cardinality();ii++) { if(Operate(i,ii)==Identity()){ _has_inverse=true; } } if(!_has_inverse){ _has_inversion=false; break; } } return(_has_inversion); } CMonoidGroup(){}; ~CMonoidGroup(){}; };
En los dos artículos anteriores, la clase monoidal y los elementos de acción monoidal no constituían datos normalizados. Esto significa que había que convertirlos a un formato que permitiera una comparación justa antes de usarlos en operaciones binarias. En este artículo nos referiremos a este formato como pesos (weights). En artículos anteriores, estos pesos se calculaban y usaban durante la ejecución. Aquí introduciremos parámetros a la clase de grupo monoidal (monoid-group) para establecer, almacenar y recuperar los valores de estos pesos dentro de la clase. Todos los pesos serán datos de tipo double.
CMonoidGroup<int> _vg; //valid inversion group CMonoidGroup<int> _ig; //invalid inversion group _vg.Weights(5); //set group size _ig.Weights(5); //set group size for(int i=0;i<5;i++) { CElement<int> _ve;_ve.Cardinality(1); _ve.Set(0,i-2); _vg.Set(i,_ve,true); //set element _vg.SetWeight(i,double(i-2)); //set weight CElement<int> _ie;_ie.Cardinality(1); _ie.Set(0,i); _ig.Set(i,_ie,true); //set element _ig.SetWeight(i,double(i)); //set weight } _vg.Operation(OP_ADD); //set monoid operation to add _vg.Identity(2); //set identity element index to 2 _ig.Operation(OP_ADD); //set monoid operation to add _ig.Identity(2); //set identity element index to 2 as above or any index printf(" it is: "+string(_vg.HasInversion())+", vg has inversion, given the weights. "); ArrayPrint(_vg.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT); printf(" it is: "+string(_ig.HasInversion())+", ig has inversion, given the weights. "); ArrayPrint(_ig.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);
Para ver este código en acción, crearemos un ejemplar del grupo monoidal y ejecutaremos una comprobación utilizando nuestras funciones de clase para ver lo que obtenemos en la salida. Nuestro código (adjunto al presente artículo) simplemente validará la inversión en el conjunto. Cada elemento deberá tener una inversión respecto al elemento de identidad.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: true, vg has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)-2, -1,0,1,2
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: false, ig has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1) 0,1,2,3,4
A efectos prácticos, al grupo monoidal '_vg' se le ha asignado un tamaño de 5, pero su tamaño real no estará limitado, ya que para cumplir todos los axiomas del grupo, cualquier emparejamiento de números en una operación binaria siempre deberá dar como resultado un número que sea miembro del conjunto del grupo. Con lo que usamos, emparejar dos y uno daría como resultado tres, y este valor no está en el conjunto. Por consiguiente, _vg será un conjunto no limitado de números enteros(Z).
Utilización de grupos monoidales en el trading algorítmico
En los dos artículos anteriores, desde que empezamos a estudiar los monoides, los hemos utilizado como puntos de decisión. En particular, se han usado en decisiones relativas a:
- la duración del periodo de análisis retrospectivo que debe considerarse;
- el marco temporal utilizado;
- el precio aplicado;
- el indicador utilizado;
- el método comercial (seguir la tendencia o negociar contra la tendencia).
Como puntos de decisión, los conjuntos de cada uno de estos monoides representaban las opciones a las que podía enfrentarse un tráder. Lo que no se mencionaba explícitamente en estos artículos, aunque se aplicaba, era la ponderación de cada elemento en los conjuntos de monoides correspondientes. Antes de realizar las operaciones binarias de los monoides sobre todos los elementos del conjunto para hacer una selección, había que normalizar los elementos del conjunto. En algunos casos (como sucede con el precio aplicado), no resultaba fácil comparar las barras de precios, cosa que requieren algunas situaciones comerciales. Así que necesitábamos encontrar una forma de cuantificar estos elementos del conjunto de una manera que se adaptara a medida que la acción del precio (o cualquier otra métrica básica elegida) cambiase con el tiempo. Así pues, esta "cuantificación" de los elementos del conjunto es lo que llamaremos pesos en este artículo.
Tras ponderar los valores de nuestros elementos para utilizar grupos, necesitaremos aplicar la función OperateModulo en la clase de acción monoidal modificada. El conjunto real de grupos que se encuentra en nuestra clase de acción no se especificará, ya que supondrá simplemente una lista de números enteros hasta el tamaño determinado por nuestra entrada para el script. Lo que se registra es un conjunto relativo para este grupo, ya que la acción por el módulo sobre el conjunto inicial provocará necesariamente repeticiones.
A continuación le mostramos la implementación de la función Operate como método con una clase de acción monoidal.
int OperateModulo(int Index,int Modulo=1) { int _operate=-1; if(Index>=0 && Index<this.Cardinality()) { int _value=int(round(set.weights[Index])); _operate=_value%Modulo; } return(_operate); }
Así, una vez transformados nuestros conjuntos monoidales en un conjunto "circular" más pequeño, la operación binaria para este monoide más pequeño, al emparejar dos elementos cualesquiera, puede dar como resultado el elemento más alejado del elemento identidad, donde, en nuestro caso, el elemento identidad será siempre el índice medio. Para establecer el tamaño del grupo monoidal, el tamaño deberá ser un número impar.
Si dos elementos son equidistantes del elemento de identidad, se seleccionará el elemento de identidad. Así que, resumiendo aquí nuestra acción monoidal, normalizaremos de forma efectiva el conjunto monoidal básico en un grupo. A continuación, tomaremos la decisión de combinar los elementos según su valor en el conjunto de acciones monoidales con la operación binaria de la acción monoidal.
Como no estamos codificando ni probando un asesor para este artículo, para ilustrar los resultados de los grupos monoidales, en cada uno de nuestros cinco parámetros mencionados imprimiremos un conjunto monoidal con las opciones a las que se enfrenta el tráder, los pesos a los que se convierten estos valores de conjunto, los valores de acción monoidal para estos pesos que dan lugar a los valores de grupo monoidal y el conjunto relativo de ese grupo de monoides. Nótese que volvemos a referirnos a los conjuntos relativos del artículo anterior, porque para tener un conjunto de acciones monoidales como grupo, usaremos un módulo del tamaño de entrada para normalizar y ajustar todos los valores de nuestros pesos al conjunto de acciones que también constituirán el grupo. Al normalizar estos valores del módulo, nos encontraremos inevitablemente con repeticiones, por lo que el conjunto de acciones no será un grupo en el sentido estricto, sino un conjunto relativo de un grupo cuyos miembros serán simplemente todos los números enteros partiendo de cero hasta el tamaño de la entrada menos uno.
Nuestros logs terminarán con los elementos del conjunto de acciones que pertenezcan al grupo, como se ha indicado anteriormente. A continuación, el lector deberá transmitir los valores calculados en cada monoide de acción del monoide de marco temporal al monoide de decisión, eligiendo según los axiomas de grupo descritos anteriormente. En un conjunto grupal, como sucede con los monoides, si alguno de los elementos emparejados fuera el elemento de identidad, tendríamos un elemento de no-identidad en la salida. Además, si los elementos emparejados son inversos entre sí, entonces tendremos un elemento de identidad en la salida.
Además, a diferencia de lo que hemos considerado en los dos artículos anteriores, podría resultar útil tomar decisiones partiendo de un marco temporal y luego utilizar un periodo de análisis retrospectivo. Así es como obtendremos nuestros pesos para el monoide de marco temporal, considerando lo anterior.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void WeighTimeframes(CMonoidGroup<ENUM_TIMEFRAMES> &G) { for(int i=0;i<G.Cardinality();i++) { ResetLastError(); int _value=0; ArrayResize(__r,3);//ArrayInitialize(_buffer,0.0);//ArraySetAsSeries(_buffer,true); if(CopyRates(_Symbol,__TIMEFRAMES[i],0,3,__r)>=3) { _value=int(round(10000.0*fabs(__r[0].close-__r[1].close)/fmax(_Point,fabs(__r[0].close-__r[1].close)+fabs(__r[1].close-__r[2].close)))); } else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); } ResetLastError(); if(!G.SetWeight(i,_value)) { printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError())); } } }
Nótese que todos los pesos se normalizarán ahora al formato entero, porque queremos utilizar el módulo cuando los convirtamos (utilizando la acción monoidal) a un conjunto relativo a un grupo. Así, como la ponderación era un valor positivo de tipo double que nunca era superior a uno, para nuestros marcos temporales la hemos convertido en un número entero, que puede ser cualquier valor de 0 a 10 000. Además, nuestro parámetro de tamaño de entrada para los marcos temporales, que por defecto es 51, será el valor que utilicemos para obtener el resto, un miembro del conjunto de grupos. Los valores restantes se almacenarán en un array de pesos de la clase de acción monoidal.
Así, si adjuntamos nuestro script al gráfico de USDJPY en el marco temporal de un minuto, veremos el siguiente resultado para el monoide de marco temporal a partir del 15.06.2023.
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)with an input size of: 21 timeframe weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)7098, 8811, 1686, 1782, 1280, 5920, 1030, 5130
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) {(0),(12),(6),(18),(20),(19),(1),(6)}
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
Utilizaremos una serie de marcos temporales ligeramente modificados de nuestros artículos anteriores. Una vez más, dependerá del lector decidir qué conjunto de marcos temporales se adapta mejor a su tema de estudio. Si representamos los logs del monoide de análisis retrospectivo, veremos lo siguiente.
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)with an input size of: 5 lookback weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)3149, 1116, 3575, 3779, 7164, 8442, 4228, 5756
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(4),(1),(0),(4),(4),(2),(3),(1)}
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 0,1,2,3,4
Podemos ver que se ha seleccionado el marco temporal de una hora en el marco temporal monoidal. La repetición de la elección final real en cada monoide siguiendo los axiomas de grupo no se implementará en este artículo ni en el código adjunto. Podrá investigar por su cuenta y dar ese primer paso en los grupos de monoides, en la dirección que crea que mejor se adapta a su estrategia. Los logs del precio utilizado con un periodo de análisis retrospectivo de 8 son los siguientes.
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)with an input size of: 21 appliedprice weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)1469254, 1586223, 1414566, 2087897 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(10),(9),(6),(14)} 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
Conclusión
Hoy hemos analizado qué son los grupos monoidales, introduciendo la noción de simetría en un monoide típico, y añadiendo el axioma adicional de que todos los miembros de un grupo monoidal deben tener inversión, mientras que las operaciones binarias entre elementos espejados deben producir siempre un elemento de identidad del grupo monoidal. El presente artículo supone la continuación de nuestro artículo anterior, en el que examinamos las acciones monoidales.
Al igual que en el artículo anterior, hemos mostrado cómo los grupos monoidales pueden ser útiles para los tráders en conjuntos restringidos. Además, hemos tomado conjuntos de monoides como un conjunto fijo de opciones para el tráder en una etapa determinada. En el artículo anterior, sin embargo, intentamos estudiar el efecto de la ampliación de los conjuntos monoidales seleccionados sobre la eficiencia del comercio.
Aquí solo hemos "insinuado" el potencial de los grupos monoidales sin mostrar los asesores que los involucran. Invitamos al lector a seguir desarrollando este tema y a implementar la posibilidad de elección en cada monoide siguiendo las reglas de los grupos que hemos mencionado pero que no hemos implementado en el código.
En el próximo artículo analizaremos un concepto más de la teoría de categorías.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/12800
- Aplicaciones de trading gratuitas
- VPS fórex gratuito por 24 horas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso