Teoria das Categorias em MQL5 (Parte 10): Grupos monoides
Introdução
No artigo anterior, avançamos em nossa análise sobre monoides, focalizando a ação dos monoides como uma ferramenta para transformar conjuntos monoides, expandindo seus elementos possíveis. Até o momento, abordamos em profundidade conceitos como domínios, morfismos e axiomas de categorias, incluindo produtos fibrados monomórficos e coprodutos fibrados epimórficos. Embora possa haver o argumento de que a compreensão completa da teoria das categorias exige um estudo mais abrangente de todos ou da maioria de seus conceitos, nossa abordagem foca em entender quais ideias são úteis sob uma perspectiva mais básica ou restrita do tema. Cada artigo desta série (ainda que em alguns casos os conceitos tenham sido inspirados por artigos precedentes) destacou a capacidade de simplificar o dia a dia dos traders e, em determinados cenários, aperfeiçoar os sistemas de negociação. Neste artigo, vamos considerar grupos monoides. Assim como as ações de monoide discutidas anteriormente, eles serão abordados como uma reinterpretação do monoide no momento da tomada de decisão sobre uma operação. Vale lembrar que as ações de monoide foram tratadas como uma expansão do conjunto monoide; aqui, faremos uma reavaliação de outro aspecto do monoide, especificamente o elemento de identidade, à medida que reconfiguramos nossos monoides novamente. O objetivo deste artigo não é desenvolver sistemas de negociação completos, como foi feito em trabalhos anteriores, onde implementamos instâncias de classes de sinais e/ou rastreamento de estratégias para compilar EAs com a ajuda do assistente integrado do MQL5. Em vez disso, focaremos em funções específicas presentes em nossos monoides codificados, ações de monoides e classes de grupos monoides, analisando sua relevância para o trader em momentos críticos de decisão.
Entendendo os grupos monoides
Para recapitular, os monoides consistem em três elementos, a saber, um conjunto, um elemento identidade que pertence a esse conjunto e uma operação binária que aceita quaisquer dois elementos desse conjunto e sempre retorna um elemento que é membro do conjunto. Além disso, se qualquer membro do conjunto estiver associado ao elemento identidade na operação binária, o resultado será sempre esse elemento. As ações de monoide, discutidas em nosso último artigo, são uma forma de função definida por um conjunto e uma operação binária que associa elementos de um conjunto monoide com o conjunto dessa função e sempre produz um elemento que é membro do conjunto da função. Vimos isso como um meio de transformar um monoide porque lembre-se de que a saída da operação binária de um monoide era fechada, pois todas as saídas eram estritamente membros do conjunto monoidal.
No entanto, seria prudente começar ressaltando que não há distinção per se entre grupos e o que estamos chamando aqui de grupos monoides. A única diferença é que estamos estritamente nos referindo a conjuntos (ou domínios) que pertencem a uma categoria. Assim, um grupo monoide, com base na definição de grupo, é um monoide com uma propriedade adicional de que cada elemento no conjunto monoidal deve ter outro elemento que seja seu inverso. Quando um elemento e seu inverso são emparelhados na operação binária do monoide, a saída é sempre o elemento de identidade do monoide.
Formalmente, a propriedade inversa que distingue o grupo de monoides
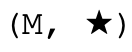
dos monoides usuais para cada
![]()
existe também um elemento inverso
![]()
tal que:
![]()
onde e é o elemento de identidade do monoide.
A implementação para traders será abordada da mesma forma que na matéria anterior. Como você deve se recordar, tratamos os monoides (conjuntos) como um leque de opções de decisão dentre as quais um trader pode optar. No artigo anterior, consideramos a possibilidade de aumentar o tamanho desse conjunto usando ações monoides. Analisamos qual seria o impacto sobre a eficiência do sistema de negociação se ampliássemos a abrangência de monoides específicos, baseando-nos em uma lista de fatores que determinam a relevância relativa dos pontos de decisão (parâmetros) desse sistema. Os resultados foram piores quando comparados ao que obtivemos no artigo que tratava dos monoides em sua forma restrita (padrão). No contexto de grupos de monoides, em vez de expandir a abrangência de nossos conjuntos, retornaremos aos monoides restritos que sofreram uma ação e foram convertidos em grupos. Estudaremos a mudança na composição do conjunto após a ação deste monoide, porém, a efetiva implementação do sistema de negociação não será objeto de discussão neste artigo. Sugiro que você explore esse assunto por conta própria.Implementando grupos monoides em MQL5
Para configurar nosso ambiente MQL5 para implementar grupos monoides, vamos iniciar a IDE e criar um novo arquivo de script usando o assistente.
Em seguida, nomeamos nosso script como 'ct_10' na próxima guia e clicamos em concluir. Este script fará referência a um arquivo de classe 'ct_10.mqh', que será uma modificação da classe que discutimos no artigo anterior 'ct_9.mqh'. Para completar, pode ser útil percorrer as etapas de criação da classe monoide, que fazia parte de 'ct_9.mqh', que mencionamos nos dois artigos anteriores. Lembre-se de que nossa unidade de construção básica é a classe de elementos, que principalmente constitui um array de objetos do tipo de dados 'T'. O tipo de dados 'T' é definido quando o elemento é inicializado.
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ template <typename T> class CElement : public CObject { protected: int cardinal; T element[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
A classe Element é chamada por um conjunto (classe de domínio) como um array.
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ template <typename T> class CDomain : public CObject { protected: int cardinal; CElement<T> elements[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
Fomos mais além e definimos não apenas a classe de categorias, que define formalmente grupos monoides como distintos de grupos, mas também classes para morfismos, homomorfismos e uma série de outros conceitos. Como elas, assim como a classe de categorias, não são essenciais para a construção de uma classe monoidal, não as listaremos nem as consideraremos neste artigo. Sabemos que um monoide é um conjunto, um elemento de identidade e uma operação binária. Se começarmos definindo o que é uma operação binária, podemos fazer isso listando nossas opções na forma de uma enumeração. Usamos algo semelhante a isso nos últimos 2 artigos.
//+------------------------------------------------------------------+ //| Enumeration for Monoid Operations | //+------------------------------------------------------------------+ enum EOperations { OP_FURTHEST=5, OP_CLOSEST=4, OP_MOST=3, OP_LEAST=2, OP_MULTIPLY=1, OP_ADD=0 };
Não abordaremos o código em detalhe no nosso artigo. O essencial é que ele determina como as operações binárias podem ser ajustadas e estabelecidas para os elementos correspondentes de um conjunto monoidal. Essa capacidade apresenta possibilidades atrativas. Ao nos referirmos à classe monoide, estabeleceremos nossa classe como publicamente herdada da classe de domínio, em vez de criar um novo classificador com uma instância do conjunto (domínio). Esse é um código eficaz, que indica claramente que um monoide é apenas um domínio com uma operação binária e um elemento de identidade associado.
//+------------------------------------------------------------------+ //| Monoid Class | //+------------------------------------------------------------------+ template <typename T> class CMonoid : public CDomain<T> { protected: //double weights[]; int identity; EOperations operation; public: double weights[]; ... void Operation(EOperations Value) { operation=Value; } EOperations Operation() { return(operation); } ... CMonoid(){ identity=0; operation=OP_ADD; }; ~CMonoid(){}; };
A esta classe, adicionaremos dois axiomas adicionais de operação binária e um elemento de identidade. No entanto, o nosso elemento de identidade não é uma nova instância do elemento. Ele já está presente no array de elementos de domínio. Apenas fazemos referência ao índice desse array que indica o nosso elemento de identidade. A classe monoide pode ser inicializada com um ponteiro automático no nosso script, conforme o exemplo subsequente.
A classe de ações monoidais, detalhada no artigo anterior, é derivada desta classe monoidal.
Contudo, quando tratamos de grupos de monoides, não há diferença semântica no código da classe entre um monoide e um grupo monoide. Podemos apenas confirmar a exigência de inversão com grupos monoides. Assim, para os nossos objetivos, a classe do grupo monoide terá uma função denominada HasInversion, conforme mostrado a seguir.
//+------------------------------------------------------------------+ //| Monoid Group Class | //+------------------------------------------------------------------+ template <typename T> class CMonoidGroup : public CMonoid<T> { protected: public: bool HasInversion() { bool _has_inversion=true; for(int i=0;i<this.Cardinality();i++) { bool _has_inverse=false; for(int ii=0;ii<this.Cardinality();ii++) { if(Operate(i,ii)==Identity()){ _has_inverse=true; } } if(!_has_inverse){ _has_inversion=false; break; } } return(_has_inversion); } CMonoidGroup(){}; ~CMonoidGroup(){}; };
Nos dois artigos anteriores, os elementos da classe monoide e as ações monoides não constituíam dados normalizados. Isso significa que, antes de usá-los em operações binárias, eles tiveram de ser convertidos em um formato que permitisse uma comparação justa. Esse formato será chamado de pesos neste artigo. Nos artigos anteriores, esses pesos foram calculados e usados em tempo de execução. Aqui, vamos introduzir parâmetros na classe monoid-group para definir, armazenar e recuperar os valores desses pesos dentro da classe. Todos os pesos serão dados do tipo double.
CMonoidGroup<int> _vg; //valid inversion group CMonoidGroup<int> _ig; //invalid inversion group _vg.Weights(5); //set group size _ig.Weights(5); //set group size for(int i=0;i<5;i++) { CElement<int> _ve;_ve.Cardinality(1); _ve.Set(0,i-2); _vg.Set(i,_ve,true); //set element _vg.SetWeight(i,double(i-2)); //set weight CElement<int> _ie;_ie.Cardinality(1); _ie.Set(0,i); _ig.Set(i,_ie,true); //set element _ig.SetWeight(i,double(i)); //set weight } _vg.Operation(OP_ADD); //set monoid operation to add _vg.Identity(2); //set identity element index to 2 _ig.Operation(OP_ADD); //set monoid operation to add _ig.Identity(2); //set identity element index to 2 as above or any index printf(" it is: "+string(_vg.HasInversion())+", vg has inversion, given the weights. "); ArrayPrint(_vg.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT); printf(" it is: "+string(_ig.HasInversion())+", ig has inversion, given the weights. "); ArrayPrint(_ig.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);
Para ver esse código em ação, vamos criar uma instância do grupo monoide e executar uma verificação usando nossas funções de classe para ver o que obtemos como resultado. Nosso código, que está anexado a este artigo, simplesmente valida a inversão no conjunto. Cada elemento deve ter uma inversão com relação ao elemento de identidade.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: true, vg has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)-2, -1,0,1,2
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: false, ig has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1) 0,1,2,3,4
Para fins práticos, o grupo monoidal '_vg' recebeu um tamanho de 5, mas seu tamanho real é ilimitado, já que para atender a todos os axiomas de um grupo, qualquer par de números na operação binária deve sempre resultar em um número que seja membro do conjunto do grupo. Com o que usamos, emparelhar dois e um resultará em três, o que não está listado no conjunto. Portanto, '_vg' é um conjunto ilimitado de inteiros (Z).
Uso de grupos monoides na negociação algorítmica
Nos dois artigos anteriores, desde que começamos a analisar monoides, os consideramos como pontos de decisão. Especificamente, eles foram usados para decidir sobre:
- o comprimento do período de análise retrospectiva a ser considerado;
- o período de tempo a ser usado;
- o preço aplicado a ser usado;
- o indicador a ser usado;
- e o método de negociação a ser adotado (se seguir a tendência ou contra a tendência).
Como pontos de decisão, os conjuntos de cada um desses monoides representavam as opções que um trader poderia se deparar. O que não foi claramente mencionado nestes artigos, embora tenha sido implementado, foi a ponderação de cada elemento nos conjuntos respectivos dos monoides. Antes de realizar as operações binárias dos monoides em todos os elementos do conjunto para fazer uma seleção, os elementos do conjunto precisavam ser normalizados. Em alguns casos, como com o preço aplicado, por exemplo, não era fácil fazer comparações com base em barra de preço por barra de preço, que é o que algumas situações de negociação exigem. Por esse motivo, tivemos que encontrar uma maneira de quantificar esses elementos do conjunto de uma forma que se adaptasse à ação do preço, ou seja, à métrica base escolhida, à medida que mudava com o tempo. Portanto, esta "quantificação" dos elementos do conjunto é o que chamaremos de pesos para este artigo.
Agora, após ponderar os valores dos nossos elementos, a fim de usar grupos, precisaríamos aplicar a função 'OperateModulo' na classe de ação monoidal modificada. O conjunto real do grupo que está em nossa classe de ação não está listado, pois é simplesmente uma lista de inteiros até um tamanho definido por nossos inputs no script. O que é registrado é um conjunto relativo a esse grupo, uma vez que a ação do módulo no conjunto inicial está destinada a gerar repetições.
A seguir, mostramos a implementação da função Operate como um método com uma classe de ação monoide.
int OperateModulo(int Index,int Modulo=1) { int _operate=-1; if(Index>=0 && Index<this.Cardinality()) { int _value=int(round(set.weights[Index])); _operate=_value%Modulo; } return(_operate); }
Então, uma vez que nossos conjuntos monoides são transformados em um conjunto menor 'circular', a operação binária para este monoide menor, ao emparelhar quaisquer dois elementos, pode resultar no elemento mais distante do elemento de identidade, onde, no nosso caso, o elemento de identidade será sempre o índice do meio. Para definir o tamanho do grupo monoide, é necessário que o tamanho seja um número ímpar.
Se dois elementos estiverem equidistantes do elemento de identidade, então o elemento de identidade é escolhido. Portanto, para recapitular, nossa ação monoidal aqui está normalizando efetivamente o conjunto monoidal base em um grupo. Em seguida, tomaremos nossa decisão a partir do emparelhamento dos elementos com base em seu valor no conjunto de ação monoidal, com a operação binária de ação monoidal.
Uma vez que não estamos codificando e testando um Expert Advisor para este artigo, para ilustrar as saídas dos grupos monoides, em cada um de nossos cinco parâmetros mencionados anteriormente, iremos imprimir o conjunto monoidal com as opções com que um trader se depara, as ponderações para as quais esses valores do conjunto são convertidos, os valores da ação monoidal nessas ponderações que resultam em valores do grupo monoidal e o conjunto relativo deste grupo monoidal. Observe que estamos nos referindo a conjuntos relativos novamente desde um artigo anterior, porque, para ter o conjunto da ação monoidal como um grupo, usaremos o módulo de um tamanho de entrada para normalizar e ajustar todos os valores de nossas ponderações em um conjunto de ação que também será um grupo. Ao normalizar esses valores com o módulo, estamos destinados a ter repetições, motivo pelo qual o conjunto de ação estritamente não é um grupo, mas um conjunto relativo a um grupo cujos membros simplesmente constituem todos os inteiros, começando do zero até o tamanho de entrada menos um.
Nossos registros de impressão concluirão nos elementos do conjunto de ação, que é relativo a um grupo, como mencionado acima. Cabe ao leitor levar adiante os valores calculados em cada ação monoidal, desde o monoide de período até o monoide de decisão, fazendo seleções seguindo os axiomas dos grupos mencionados anteriormente. Apenas para reiterar, em um conjunto de grupos, assim como nos monoides, se algum dos elementos emparelhados for o elemento de identidade, o resultado será um elemento não identidade, e além disso, se os elementos emparelhados forem inversos um do outro, o resultado será o elemento de identidade.
Além disso, pode ser esclarecedor fazer seleções começando pelo período de tempo e depois pelo período de análise retrospectiva, ao contrário do que consideramos nos dois artigos anteriores. Veja como obtemos nossos pesos para o período de tempo monoide com base no exposto acima.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void WeighTimeframes(CMonoidGroup<ENUM_TIMEFRAMES> &G) { for(int i=0;i<G.Cardinality();i++) { ResetLastError(); int _value=0; ArrayResize(__r,3);//ArrayInitialize(_buffer,0.0);//ArraySetAsSeries(_buffer,true); if(CopyRates(_Symbol,__TIMEFRAMES[i],0,3,__r)>=3) { _value=int(round(10000.0*fabs(__r[0].close-__r[1].close)/fmax(_Point,fabs(__r[0].close-__r[1].close)+fabs(__r[1].close-__r[2].close)))); } else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); } ResetLastError(); if(!G.SetWeight(i,_value)) { printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError())); } } }
Observe que todas as ponderações agora serão normalizadas para o formato inteiro, porque desejamos usar o módulo para convertê-las, por meio da ação monoidal, em um conjunto relativo a um grupo. Por isso, para nossos períodos de tempo, uma vez que a ponderação era um número real positivo que nunca era superior a um, isso será convertido em um número inteiro que pode ser qualquer valor de 0 a 10.000. Além disso, nosso parâmetro de tamanho de entrada para os períodos de tempo, com padrão em 51, será o valor que usamos para obter o resto, um membro do conjunto do grupo. Os valores do resto são armazenados no array de ponderações da classe de ação monoidal.
Assim, se anexarmos nosso script ao gráfico de USDJPT no período de um minuto, a partir de algum momento em 15/06/2023, este foi o resultado para o monoide de período de tempo.
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)with an input size of: 21 timeframe weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)7098, 8811, 1686, 1782, 1280, 5920, 1030, 5130
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) {(0),(12),(6),(18),(20),(19),(1),(6)}
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
Estamos usando um conjunto ligeiramente modificado de períodos de tempo em relação aos nossos artigos anteriores. Novamente, cabe a você escolher uma faixa de períodos de tempo que seja a melhor para o que você está estudando. Se exibirmos o log do monoide da análise retrospectiva, veremos o seguinte.
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)with an input size of: 5 lookback weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)3149, 1116, 3575, 3779, 7164, 8442, 4228, 5756
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(4),(1),(0),(4),(4),(2),(3),(1)}
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 0,1,2,3,4
Vemos que o período de uma hora foi selecionado no período monoide. Para repetir, a seleção real final em cada monoide, seguindo os axiomas do grupo, não está implementada neste artigo ou código anexado. Isso fica a cargo do leitor explorar e dar o primeiro passo nos grupos monoides na direção que considerarem melhor para sua estratégia. Os logs do preço usado com o período retrospectivo igual a 8 são os seguintes.
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)with an input size of: 21 appliedprice weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)1469254, 1586223, 1414566, 2087897 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(10),(9),(6),(14)} 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
Considerações finais
Consideramos o que são grupos monoides ao introduzir o conceito de simetria em um monoide típico, no qual adicionamos o axioma adicional de que todos os membros de um grupo monoidal precisam ter um inverso, e também que operações binárias entre elementos espelhados são restritas a sempre produzir o elemento de identidade do grupo monoidal. Esta foi uma continuação de nosso artigo anterior, no qual analisamos as ações monoidais.
Como no artigo anterior, mostramos como os grupos de monoides podem ser úteis para traders em conjuntos monoides restritos. Naquele artigo, consideramos conjuntos monoides como um conjunto fixo de escolhas de um trader em um determinado estágio. Isso é diferente da abordagem de ações monoides que adotamos no último artigo, onde exploramos os impactos da expansão de conjuntos monoides selecionados no desempenho da negociação.
Ao apenas "sugerir" o potencial dos grupos monoides e não apresentar Expert Advisors que os utilizem, como fizemos nos dois artigos anteriores, convidamos o leitor a explorar mais a fundo este material, implementando seleções em cada monoide seguindo as regras dos grupos que mencionamos, mas não codificamos.
Em nosso próximo artigo, abordaremos outro conceito da teoria de categorias.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/12800
- Aplicativos de negociação gratuitos
- VPS Forex grátis por 24 horas
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso