Algorithmes d'optimisation de la population : Optimisation des Colonies de Fourmis (Ant Colony Optimization - ACO)
Le grand secret de tout comportement est le comportement social...
F. Bartlett
Sommaire
1. Introduction
2. Principes de l'algorithme
3. Version modifiée
4. Résultats des tests
1. Introduction
Le chercheur belge Marco Dorigo a créé un modèle mathématique qui décrit scientifiquement le processus d'intelligence collective d’une colonie de fourmis. Il l'a publié dans sa thèse de doctorat en 1992 et l'a implémenté sous forme d'algorithme. L'optimisation des colonies de fourmis (ACO) est une méthode de recherche stochastique basée sur la population pour résoudre un large éventail de problèmes d'optimisation combinatoire. L’ACO est basé sur le concept de « stigmergie ». En 1959, Pierre-Paul Grasset invente la théorie de la stigmergie pour expliquer le comportement de nidification des termites. Stigmergy se compose de deux mots grecs : stigma (signe) et ergon (action).
La définition canonique est un type d'interaction indirecte entre les membres d'une population prolongée dans le temps par l'interaction avec l'environnement. En d'autres termes, l'un des agents laisse une trace ou modifie d'une manière ou d'une autre les paramètres régionaux afin qu'un autre agent reçoive des informations lorsqu'il entre dans sa zone. Dans le cas des fourmis, la stigmergie est constituée de phéromones. Un exemple de stigmergie est la communication des fourmis dans le processus de recherche de nourriture : les fourmis communiquent indirectement entre elles, laissant des traînées de phéromones sur le sol et influençant ainsi les processus de prise de décision des autres fourmis. Cette forme simple de communication entre les fourmis individuelles donne lieu au comportement et aux capacités complexes de la colonie dans son ensemble.
Les fourmis sont des insectes sociaux, elles vivent en colonies. Le comportement des fourmis est contrôlé par le but de rechercher de la nourriture. Tout en cherchant, elles parcourent leurs colonies. La fourmi saute à plusieurs reprises d'un endroit à un autre à la recherche de nourriture. En se déplaçant, elle dépose sur le sol un composé organique appelé phéromone. Ainsi, les fourmis communiquent entre elles à l'aide des traces de phéromones.
Lorsqu'une fourmi trouve de la nourriture, elle en transporte autant qu'elle peut. Au retour, elle dépose des phéromones en cours de route, en fonction de la quantité et de la qualité des aliments. D'autres fourmis peuvent ainsi suivre cette route à leur tour. Plus le niveau de phéromone est élevé, plus la probabilité de choisir ce chemin particulier est élevée. Et plus les fourmis passent par un chemin particulier, plus il restera de phéromones sur ce chemin.
Voyons l'exemple suivant : supposons qu'il existe 2 façons d'obtenir de la nourriture pour la colonie. Au début, il n'y a pas de phéromone au sol. La probabilité de choisir l’une de ces 2 voies est donc égale (50%). Supposons que deux fourmis choisissent deux chemins différents vers la nourriture. Les distances de ces deux chemins sont différentes. La fourmi empruntant le chemin le plus court arrivera à la nourriture avant l'autre. Lorsqu'elle trouve la nourriture, elle en prend une partie et retourne à la colonie. En retraçant son chemin, elle dépose une phéromone sur le sol. La fourmi prenant un chemin plus court atteindra la colonie plus tôt.
Lorsque la troisième fourmi veut sortir à la recherche de nourriture, elle empruntera un chemin plus court en fonction du niveau de phéromone au sol. Parce que le chemin le plus court a plus de phéromones que le plus long, la troisième fourmi suivra le chemin qui a le plus de phéromones. Au moment où la fourmi, suivant le chemin le plus long, est revenue à la colonie, plus de fourmis auront déjà emprunté le chemin avec des niveaux plus élevés de phéromones. Lorsqu'une autre fourmi essaie ensuite de se rendre à sa destination (nourriture) depuis la colonie, elle constatera que chaque chemin a le même niveau de phéromones. Elle en choisira donc un au hasard. En répétant ce processus encore et encore, et après un certain temps, le chemin le plus court gagnera plus de phéromones que les autres et la probabilité que les fourmis empruntent ce chemin sera plus élevée.
L'algorithme ACO est une sorte d'algorithme d'intelligence en essaim. En modélisant le processus de recherche de nourriture d'une colonie de fourmis, le chemin le plus court dans divers environnements est établi à l'aide du mécanisme de transfert de données interne de la colonie de fourmis. Plus la concentration de phéromone restant sur le chemin est élevée, plus la probabilité que la fourmi choisisse ce chemin est élevée. Dans le même temps, la concentration de phéromones diminue avec le temps. Par conséquent, en raison du comportement de la colonie, les fourmis apprennent et optimisent constamment grâce à un mécanisme de rétroaction pour déterminer le chemin de recherche de nourriture le plus court. L'algorithme ACO est largement utilisé dans la planification de trajectoire.
2. Principes de l'algorithme
Dans l’ACO, un ensemble d'agents logiciels appelés fourmis artificielles recherchent de bonnes solutions à un problème d'optimisation donné. Pour appliquer l’ACO, le problème d'optimisation est transformé en problème de recherche du meilleur chemin sur un graphe pondéré. Les fourmis artificielles (appelées ici fourmis) construisent progressivement des solutions se déplaçant le long du graphique. Le processus de construction d'une solution est stochastique et dépend du modèle de phéromones : un ensemble de paramètres associés aux composants du graphe (nœuds ou arêtes) dont les valeurs sont modifiées par les fourmis lors de l'exécution.
Considérons l'algorithme du problème du voyageur de commerce : nous avons un ensemble d'emplacements (villes) et de distances entre eux. Le problème est de trouver un chemin fermé de longueur minimale qui ne visite chaque ville qu'une seule fois. Un graphe défini en associant un ensemble de villes à un ensemble de sommets de graphe est appelé graphe de construction. Puisqu'il est possible de se déplacer d'une ville donnée vers n'importe quelle autre ville, le graphe de construction est entièrement connecté et le nombre de sommets est égal au nombre de villes. Nous fixons des longueurs d'arête entre les sommets proportionnelles aux distances entre les villes représentées par ces sommets. Et nous associons des valeurs de phéromones et des valeurs heuristiques aux arêtes du graphe. Les valeurs de phéromone changent au moment de l'exécution et représentent l'expérience cumulée de la colonie de fourmis, et les valeurs heuristiques sont des valeurs dépendantes du problème.
Les fourmis construisent des solutions de la manière suivante : Chaque fourmi part d'une ville choisie au hasard (un sommet du graphe de construction). Puis, à chaque étape de construction, elle se déplace le long des bords du graphe. Chaque fourmi stocke la mémoire de son chemin. Aux étapes suivantes, elle choisit parmi les arêtes qui ne mènent pas aux sommets déjà visités. La fourmi a construit une solution dès qu'elle a visité tous les sommets du graphe. A chaque étape de construction, la fourmi choisit de façon probabiliste une arête à suivre parmi celles qui mènent à des sommets encore non visités. La règle probabiliste est basée sur les valeurs de phéromones et sur les informations heuristiques : plus la valeur de phéromone et heuristique associée à un bord est élevée, plus la probabilité que la fourmi choisisse ce bord particulier est élevée. Une fois que toutes les fourmis ont terminé leur voyage, les phéromones aux bords sont mises à jour. Chacune des valeurs de phéromone est initialement réduite d'un certain pourcentage. Cette procédure est répétée jusqu'à ce que le critère de fin soit satisfait.
La communication basée sur les phéromones est l'une des méthodes de communication les plus efficaces répandues dans la nature. Les phéromones sont utilisées par les insectes sociaux tels que les abeilles, les fourmis et les termites pour la communication entre les agents. En raison de leur faisabilité, les phéromones artificielles ont été adoptées dans les systèmes multi-robots et en essaim.
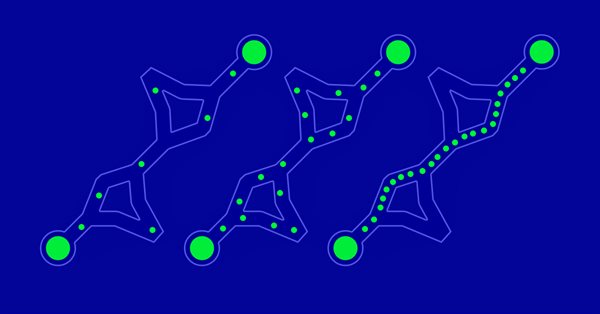
Comment comprendre que nos fourmis aient vraiment trouvé le chemin le plus court ? Il existe un excellent cas de test pour cela : des points disposés en cercle. Le chemin le plus court sera toujours le même - un cercle.
Le premier algorithme ACO s'appelait le système des fourmis. Il visait à résoudre le problème du voyageur de commerce, dont le but est de trouver le chemin le plus court aller-retour pour relier un certain nombre de villes. L'algorithme général est relativement simple et repose sur un ensemble de fourmis, pour lequel chacune fait un tour possible des villes. A chaque étape, la fourmi choisit un chemin d'une ville à l'autre selon quelques règles :
- Elle doit visiter chaque ville exactement une fois ;
- Une ville éloignée a moins de chances d'être sélectionnée (visibilité) ;
- Plus la traînée de phéromones posée à la frontière entre deux villes est forte, plus il est probable que cette frontière soit choisie ;
- Ayant terminé son chemin, la fourmi dépose plus de phéromones sur toutes les arêtes qu'elle a traversées si le chemin est court ;
- Après chaque itération, les traînées de phéromones s'évaporent.

Fig. 1 : Un exemple de cheminements possibles avec 5 points nodaux
3. Version modifiée
Plusieurs des variantes les plus populaires des algorithmes ACO sont connues. Voyons-les :
Système de Fourmis (AS)
Le système de fourmis est le premier algorithme ACO.
Système de Colonies de Fourmis (ACS)
Dans l'algorithme du système de colonies de fourmis, le système de fourmis d'origine a été modifié sous 3 aspects :
1. La sélection des bords est biaisée vers l'exploitation (c'est-à-dire en faveur de la probabilité de choisir les bords les plus courts avec plus de phéromones) ;
2. Lors de la construction d'une solution, les fourmis modifient le niveau de phéromones sur les bords qu'elles choisissent en appliquant une règle de mise à jour locale des phéromones ;
3. A la fin de chaque itération, seule la meilleure fourmi peut mettre à jour les traces en appliquant la règle de mise à jour globale des phéromones modifiée.
Système de Fourmis Elite
Dans cet algorithme, la meilleure solution globale dépose la phéromone sur sa piste après chaque itération (même si la piste n'a pas été revisitée) avec toutes les autres fourmis. Le but de la stratégie élite est de diriger la recherche de toutes les fourmis pour construire une solution contenant les liens du meilleur itinéraire actuel.
Système de Fourmis max-min (MMAS)
Cet algorithme contrôle le nombre maximum et minimum de phéromones sur chaque piste. Seule la meilleure tournée mondiale ou la meilleure tournée répétée peut ajouter des phéromones à son parcours. Pour éviter la stagnation de l'algorithme de recherche, la plage des quantités possibles de phéromones sur chaque trace est limitée par l'intervalle [τ max, τ min]. Toutes les arêtes sont initialisées avec τ max pour accélérer l'exploration de la solution. Les traces sont réinitialisées à τ max à l'approche de la stagnation.
Système de Fourmis basé sur les rangs (Asrank)
Toutes les solutions sont classées en fonction de leur longueur. Seul un nombre fixe des meilleures fourmis de cette itération peuvent mettre à jour leurs défis. La quantité de phéromone déposée est pesée pour chaque solution, de sorte que les solutions avec des trajets plus courts déposent plus de phéromone que les solutions avec des trajets plus longs.
Optimisation parallèle des Colonies de Fourmis (PACO)
Système de colonies de fourmis (ACS) avec des stratégies de communication.
Les fourmis artificielles sont divisées en plusieurs groupes. 7 méthodes de communication sont proposées pour mettre à jour les niveaux de phéromones entre les groupes de l'ACS qui travaillent sur le problème du voyageur de commerce.
Colonie de Fourmis Orthogonales Continues (COAC)
Le mécanisme de dépôt de phéromones COAC permet aux fourmis de rechercher des solutions de manière collaborative et efficace. En utilisant la méthode de conception orthogonale, les fourmis dans la zone autorisée peuvent explorer rapidement et efficacement les zones choisies avec des capacités et une précision de recherche globale améliorées. La méthode de conception orthogonale et la méthode de réglage adaptatif du rayon peuvent également être étendues à d'autres algorithmes d'optimisation pour fournir des avantages plus larges dans la résolution de problèmes pratiques.
Optimisation Récursive d'une Colonie de Fourmis
Il s'agit d'une forme récursive d'une colonie de fourmis qui divise toute la zone de recherche en plusieurs sous-domaines et résout le problème dans ces sous-domaines. Les résultats de tous les sous-domaines sont comparés et les meilleurs passent au niveau suivant. Les sous-domaines correspondant aux résultats sélectionnés sont ensuite subdivisés et le processus est répété jusqu'à ce que la précision souhaitée soit obtenue. Cette méthode a été testée sur des problèmes d'inversion géophysique incorrecte prouvant son efficacité.
Les algorithmes de colonies de fourmis considérés ci-dessus ont été développés à l'origine pour résoudre des problèmes d'optimisation sur des graphes. Le problème est intégré dans ces algorithmes et les conditions du problème sont données comme paramètres (les coordonnées des nœuds du graphe). Les algorithmes basés sur les principes ACO sont ainsi hautement spécialisés. Mais ces algorithmes ne sont pas applicables à nos tâches car nous n'utilisons pas de coordonnées fixes. Nous pouvons avoir n'importe quelles coordonnées, y compris des coordonnées similaires. Pour résoudre un large éventail de problèmes d'optimisation dans le domaine du trading d'instruments financiers (y compris la formation de réseaux de neurones), nous devons développer un nouvel algorithme universel, afin qu'il puisse passer nos tests spéciaux, c'est-à-dire qu'il devrait s'agir d'un tout nouvel ACO.
Réfléchissons au concept de base de ce nouvel algorithme. Tout comme dans la version canonique, nous aurons une colonie de fourmis. On ne peut pas baliser les chemins parcourus avec des phéromones, elles peuvent aller n'importe où dans un espace multidimensionnel, mémoriser et sauvegarder des itinéraires. Un pas continu ne semble pas approprié, car la probabilité d'emprunter le même itinéraire tend vers zéro. Et il n'est pas du tout nécessaire de mémoriser les nœuds, car il n'y a pas de problème de passage séquentiel sans répétitions : il est nécessaire de retirer le problème de l'algorithme. Alors que devrions-nous faire? A ce stade, on ne sait absolument pas quelle direction prendre dans le développement du concept.
Ainsi, encore une fois, nous notons les principaux points qui distinguent notre nouvel algorithme de l’algorithme canonique :
1. Il n'y a pas de points fixes dans l'espace.
2. Il n'est pas nécessaire de parcourir le chemin dans un certain ordre.
3. Puisqu'il n'y a pas de chemins, il n'y a rien à marquer avec des phéromones.
Découvrons ensuite ce que nous avons en tête en gardant à l'esprit l'idée d'une colonie de fourmis. Nous pouvons marquer avec des phéromones les points mêmes où les fourmis ont marché, mais pas le chemin qu'elles ont parcouru. Définissons la valeur de la fonction de fitness comme le nombre de phéromones à l'emplacement de la fourmi à l'itération actuelle. Les fourmis devront ensuite se déplacer vers les coordonnées où se trouvent le plus de phéromones. Mais nous pouvons rencontrer un problème lorsque toutes les fourmis courent simplement vers un seul point, celui qui a le plus de phéromones. Ce n'est pas nécessairement la meilleure solution au problème étant donné que les points sont les variables de la fonction optimisée. Nous nous souvenons qu'en ACO classique, la longueur du chemin vers le nœud compte également. Plus le chemin choisi est court, mieux c'est. Nous devons donc calculer la distance entre l'emplacement actuel et l'endroit où la fourmi doit aller. L'endroit suivant est celui où se trouvent les autres fourmis. C'est-à-dire que nous acceptons le concept selon lequel les fourmis se déplacent les unes vers les autres avec une certaine quantité de hasard.
Quel genre d'aléatoire pouvons-nous ajouter au mouvement ?
- Tout d'abord, ajoutons le facteur aléatoire lors du choix de la position suivante PheromoneEffect_P.
- Ensuite, ajoutons un facteur aléatoire tenant compte de la distance à la position suivante PathLengthEffect_P (plus la distance est petite, meilleur est le choix).
Nous avons donc 2 critères pour choisir la position suivante : la quantité de phéromones dans chaque position spécifique où se trouvent les fourmis et la distance entre tous ces points par paires. Mais, même si nous le faisons en utilisant uniquement ces 2 critères de sélection, les fourmis se déplaceront dans l'espace le long des bords d'une figure imaginaire, dont les nœuds sont leur propre emplacement. Il n'y aura donc aucun progrès dans la recherche d'un meilleur endroit.
Dans ce cas, ajoutons le rayon d'influence de la phéromone PheromoneRadius_P (rapport de la distance entre les points), à l'intérieur duquel les fourmis peuvent la sentir. Les fourmis pourront ensuite passer au-delà du point où elles se sont déplacées. Cela donnera un degré de liberté supplémentaire aux fourmis lorsqu'elles se déplacent dans l'espace multidimensionnel.
Pour que les fourmis explorent de nouvelles zones, elles doivent être autorisées à s'écarter du vecteur de direction le long de n'importe laquelle des coordonnées. Introduisons le rapport PathDeviation_P qui donnera l'écart par rapport à l'incrément à une coordonnée spécifique. Puisque nous avons un espace multidimensionnel, suivant le vecteur de déplacement, certaines coordonnées peuvent avoir un incrément positif, et d'autres peuvent avoir un incrément négatif. Les incréments peuvent avoir des valeurs modulo différentes. Ce rapport permettra de prendre en compte tout cela et donnera un certain degré de liberté aux fourmis dans la recherche de nourriture (l'extremum de la fonction).
Alors, quel est le vecteur de déplacement et comment mesure-t-on la distance que la fourmi doit parcourir ? Pour répondre à ces questions, utilisons l'équation de calcul de la distance entre 2 points dans l'espace tridimensionnel :
![]()
Une représentation visuelle du vecteur de déplacement peut être obtenue en regardant la figure 2 :
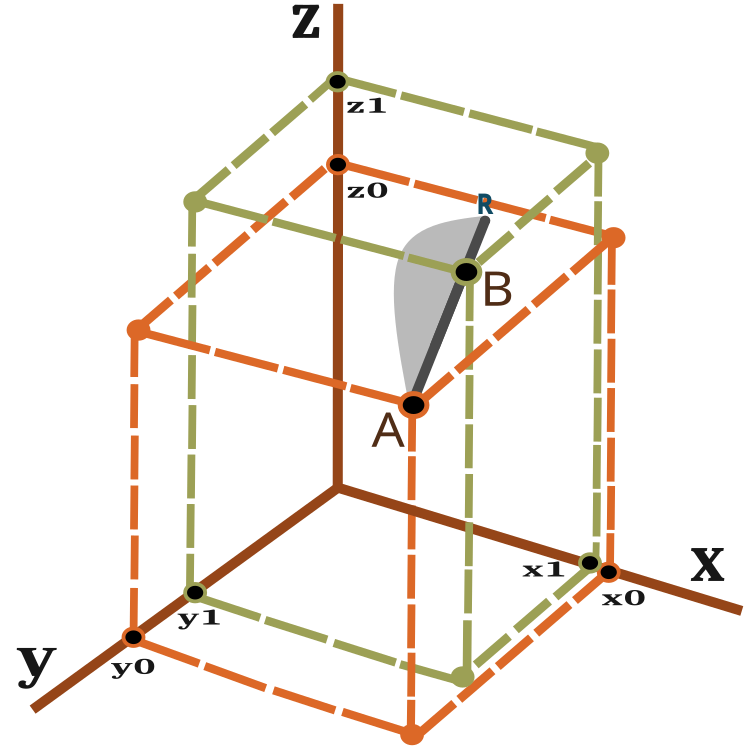
Fig. 2 : Vecteur de déplacement d’une fourmi
Pour les espaces à n dimensions, le calcul est similaire.
Une fourmi sur une itération (époque) se déplace du point A au point B avec un glissement possible vers le point R. La distance entre le point R et le point B dépend du rapport PheromoneRadius_P et peut être calculée comme BR = AB x PheromoneRadius_P.
La probabilité d'un nouvel emplacement sur la ligne AR est illustrée à la figure 2 sous forme de zone grise schématiquement (pas à l'échelle). Ainsi, le nouvel emplacement de la fourmi est plus susceptible de tendre vers le point B. Le principe du décalage de probabilité a été abordé dans l'articleprécédent.
L'algorithme comprend les étapes suivantes à chaque itération :
1) Positionnement aléatoire des fourmis dans l'espace.
2) Détermination de la valeur de la quantité de phéromone (fonction fitness) pour les fourmis.
3) Calcul de la distance d'une fourmi à une autre.
4) Choix du point préféré où la fourmi se déplacera.
5) Calcul de la probabilité d'un point sur le vecteur AR.
6) Calcul des coordonnées du point obtenu sur le vecteur AR.
7) Répétition à partir de l'étape 2 jusqu'à ce que la condition d'arrêt soit remplie.
Passons à la description du code de l'algorithme. Ecrivons tout d’abord une structure contenant une description de la fourmi, avec :
- c[] - les coordonnées de la fourmi,
- cLast[] - les coordonnées précédentes,
- cB [] - les meilleures coordonnées pour toutes les itérations,
- f - la valeur actuelle de la phéromone,
- fB - la valeur maximale de phéromone atteinte dans toutes les itérations.
Dans le constructeur de la structure ant, nous initialisons la valeur de f et fB avec la valeur minimale possible pouvant être représentée par le type 'double'.
//—————————————————————————————————————————————————————————————————————————————— struct S_Ants { double cLast []; //last coordinates double c []; //coordinates double cB []; //best coordinates double f; //pheromone of the current coordinates double fB; //pheromone of the best coordinates S_Ants () { f = -DBL_MAX; fB = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Nous avons besoin d'une structure dont le tableau nous permettra de stocker les distances par paires entre toutes les fourmis.
struct S_Paths { double a []; };
Je vais écrire notre algorithme ACO modifié sous forme de classe, dans laquelle il n'y a encore que 3 méthodes publiques qui sont suffisantes et nécessaires dans le cadre de la construction d'un algorithme d'optimisation :InitAnts(), Preparation() et Dwelling(). Il existe également des méthodes privées GenerateRNDants() et AntsMovement(), ainsi que d'autres méthodes privées qui sont déjà devenues standard pour nos algorithmes. Le tableau de structure ants[] correspond à une colonie de fourmis.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACO { public: //---------------------------------------------------------------------------- S_Ants ants []; //ants double rangeMax []; //maximum search range double rangeMin []; //manimum search range double rangeStep []; //step search double cB []; //best coordinates double fB; //pheromone of the best coordinates void InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP); void Preparation (); void Dwelling (); private: //---------------------------------------------------------------------------- S_Paths paths []; int coordinates; //number of coordinates int antHillSize; //ant hill size double goals []; double pheromoneEffect; double pathLengthEffect; double pheromoneRadius; double pathDeviation; bool dwelling; void GenerateRNDants (); void AntsMovement (); double SeInDiSp (double in, double inMin, double inMax, double step); double RNDfromCI (double min, double max); double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
Dans la méthode d'initialisation, affectons des valeurs initiales aux variables et à la taille du tableau.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP) { fB = -DBL_MAX; coordinates = coordinatesP; antHillSize = antHillSizeP; pheromoneEffect = pheromoneEffectP; pathLengthEffect = pathLengthEffectP; pheromoneRadius = pheromoneRadiusP; pathDeviation = pathDeviationP; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); dwelling = false; ArrayResize (ants, antHillSize); ArrayResize (paths, antHillSize); for (int i = 0; i < antHillSize; i++) { ArrayResize (ants [i].c, coordinates); ArrayResize (ants [i].cLast, coordinates); ArrayResize (ants [i].cB, coordinates); ArrayResize (paths [i].a, antHillSize); } ArrayResize (cB, coordinates); ArrayResize (goals, antHillSize); } //——————————————————————————————————————————————————————————————————————————————
La méthode Preparation() est appelée en premier à chaque itération.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Preparation () { if (!dwelling) { fB = -DBL_MAX; GenerateRNDants (); dwelling = true; } else AntsMovement (); } //——————————————————————————————————————————————————————————————————————————————
La méthode GenerateRNDants() est responsable de la création d'une colonie de fourmis aléatoire. Les coordonnées des fourmis sont attribuées au hasard dans les limites données.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::GenerateRNDants () { for (int s = 0; s < antHillSize; s++) { for (int k = 0; k < coordinates; k++) { ants [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); ants [s].c [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); ants [s].cLast [k] = ants [s].c [k]; ants [s].cB [k] = ants [s].c [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Stockons les coordonnées actuelles des fourmis dans la méthode Dwelling() et mettons à jour les valeurs maximales de phéromones obtenues au moment de l'itération en cours.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Dwelling () { for (int i = 0; i < antHillSize; i++) { ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY); //remember the best coordinates for the ant if (ants [i].f > ants [i].fB) { ants [i].fB = ants [i].f; ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY); } //remember the best coordinates for the anthill if (ants [i].f > fB) { fB = ants [i].f; ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
La méthode principale de l'algorithme AntsMovement() effectue les actions suivantes : calcul de la distance d'une fourmi à l'autre, calcul du choix d'un point préféré où la fourmi se déplacera, calcul de la probabilité d'un point sur le vecteur AR. Calcul des coordonnées du point obtenu sur le vecteur AR.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::AntsMovement () { double rndPh; double rndPt; double summCoordinates = 0.0; double scores []; ArrayResize (scores, antHillSize); double maxPh = -DBL_MAX; double minPh = DBL_MAX; double maxPt = -DBL_MAX; double minPt = DBL_MAX; double goal; double goalBest = -DBL_MAX; int goalInd = 0; //measure the distance between all the ants----------------------------------- for (int i = 0; i < antHillSize; i++) { for (int k = 0; k < antHillSize; k++) { if (i == k) { paths [i].a [k] = DBL_MAX; continue; } for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0); paths [i].a [k] = pow (summCoordinates, 0.5); if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k]; if (minPt > paths [i].a [k]) minPt = paths [i].a [k]; } } //---------------------------------------------------------------------------- for (int i = 0; i < antHillSize; i++) { maxPh = -DBL_MAX; minPh = DBL_MAX; for (int k = 0; k < antHillSize; k++) { if (i != k) { if (maxPh < ants [k].f) maxPh = ants [k].f; if (minPh > ants [k].f) minPh = ants [k].f; } } goalBest = -DBL_MAX; goalInd = 0; for (int k = 0; k < antHillSize; k++) { if (i != k) { rndPh = RNDfromCI (0.0, pheromoneEffect); rndPt = RNDfromCI (0.0, pathLengthEffect); goal = Scale (ants [k].f, minPh, maxPh, 0.0, 1.0, false) * rndPh * Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true) * rndPt; if (goalBest < goal) { goalBest = goal; goalInd = k; } } } double wayToGoal = paths [i].a [goalInd]; double radiusNearGoal = wayToGoal * pheromoneRadius; double endWay = wayToGoal + radiusNearGoal; double x = RNDfromCI (-1.0, 1.0); double y = x * x; if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay, false); else y = Scale (y, 0.0, 1.0, 0.0, wayToGoal, true); for (int j = 0; j < coordinates; j++) { double incrementFactor = y / wayToGoal; double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j]; ants [i].c [j] = ants [i].cLast [j] + (coordDistance * incrementFactor); double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation; ants [i].c [j] += w; ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Il convient de prêter attention à la fonction de mise à l'échelle d'un nombre d'une plage numérique à une autre. J'y ai déjà pensé dans des articles précédents. Je vais cette fois étendre ses fonctionnalités. L'entrée d'inversion est utilisée pour modifier le sens de mise à l'échelle, comme illustré dans la figure ci-dessous :
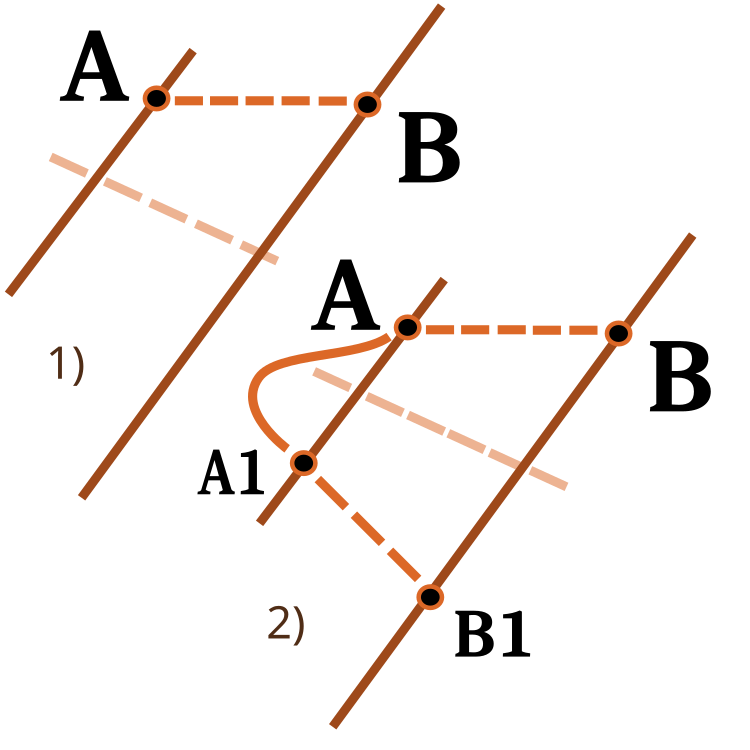
Fig. 3 : Mise à l'échelle d'un nombre d'une plage numérique à une autre.
1) Mise à l'échelle directe - 2) Mise à l'échelle inversée
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return revers ? OutMAX : OutMIN; if (In > InMAX) return revers ? OutMIN : OutMAX; double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); if (!revers) return res; else return OutMAX - res; } } //——————————————————————————————————————————————————————————————————————————————
4. Résultats des tests
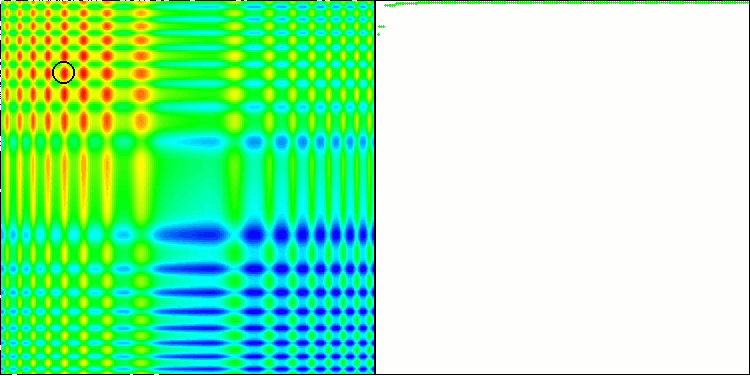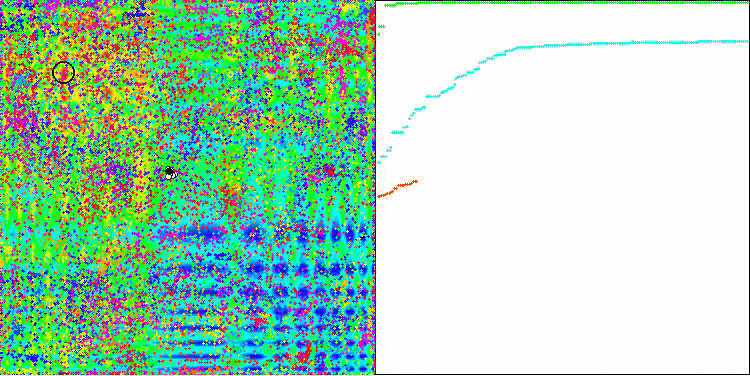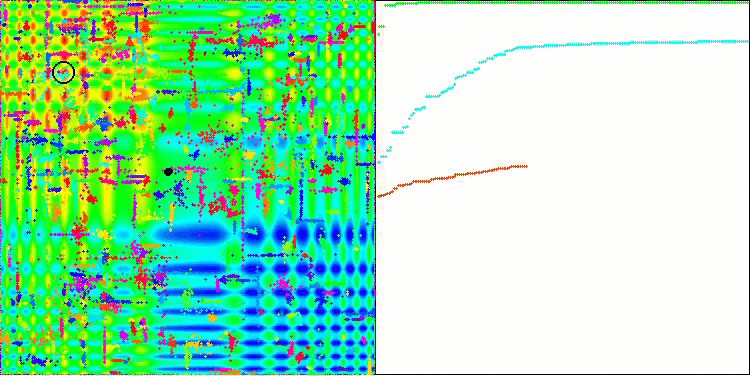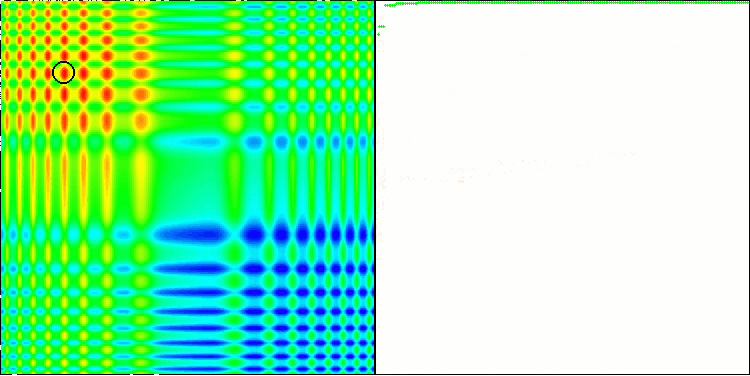
ACO sur la fonction de test Skin.
ACO sur la fonction de test Forest.
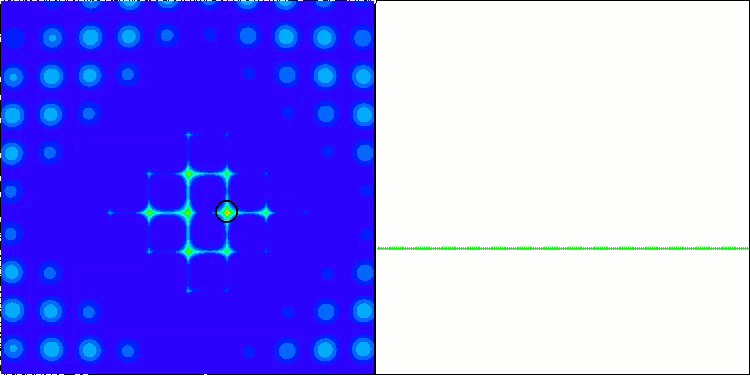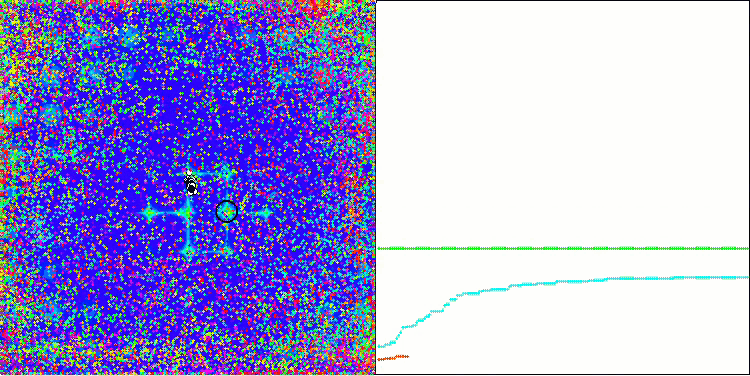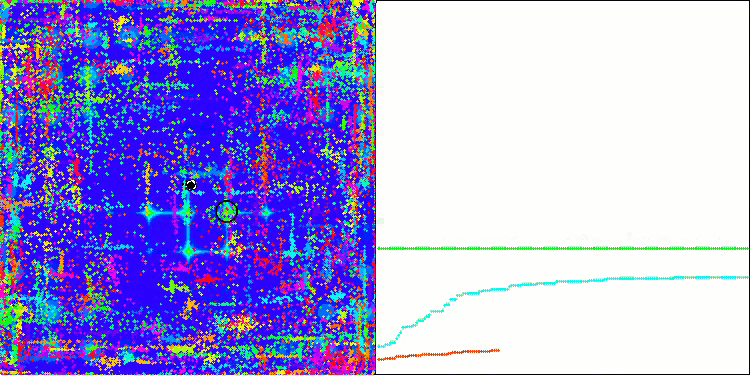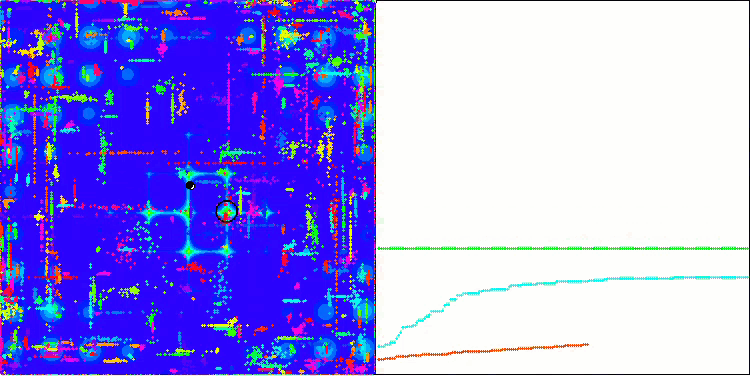
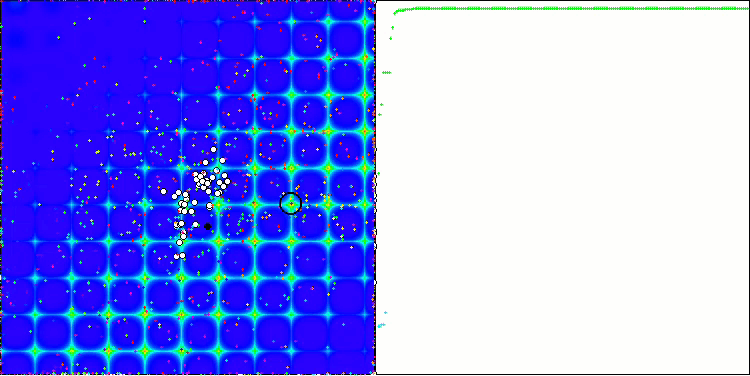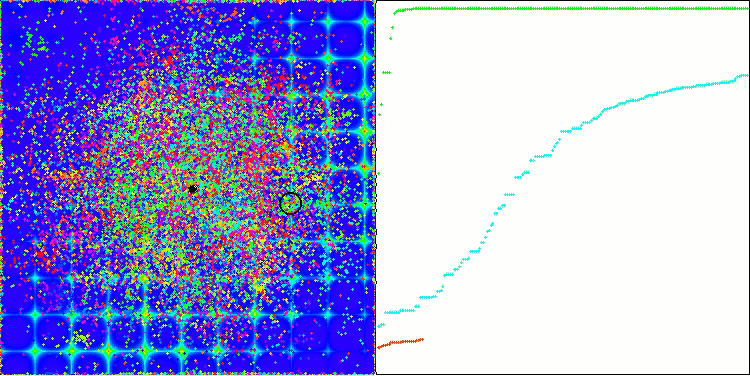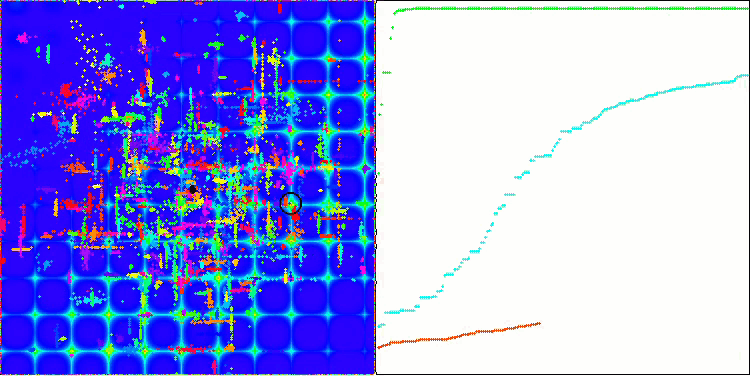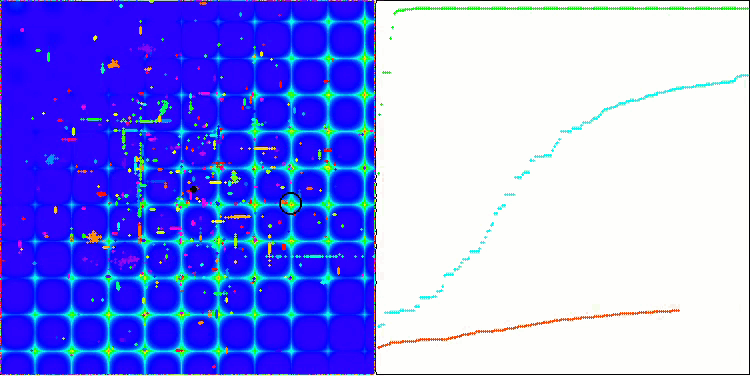
ACO la fonction de test Megacity.
Il est maintenant temps de tirer des conclusions. D'une part, l'algorithme conventionnel Ant Colony n'est pas applicable aux problèmes d'optimisation pour le trading d'instruments financiers. Pourtant, dans une tentative d'éviter les limites de la version conventionnelle, nous avons assisté à l'émergence d'un tout nouveau concept de l'algorithme Colonie de Fourmis permettant un développement ultérieur de l'ACO. Ce type d’algorithme peut déjà être appliqué à un large éventail de problèmes, y compris le problème du voyageur de commerce.
Nous avons également maintenant un nouveau leader dans la table de notation. Examinons les résultats plus en détail. Faites tout d’abord attention aux résultats des tests :
2022.10.27 16:46:28.678 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) 1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) Score1: 0.99502; Score2: 0.99599 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) 20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) Score1: 0.69826; Score2: 0.86403 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) 500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) Score1: 0.50498; Score2: 0.58800 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) 1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) Score1: 0.99087; Score2: 0.99302 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) 20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) Score1: 0.22374; Score2: 0.65571 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) 500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) Score1: 0.08408; Score2: 0.17442 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) 1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) Score1: 0.78667; Score2: 0.78667 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) 20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) Score1: 0.11667; Score2: 0.26133 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) 500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) Score1: 0.04224; Score2: 0.08208 2022.10.27 16:49:41.075 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) All score for C_AO_ACO: 0.5468768583006471
L'algorithme s'est bien comporté sur la fonction Skin lisse, démontrant une excellente convergence et de bonnes capacités de mise à l'échelle, étant particulièrement bien en avance dans les tests de 20 et 500 fonctions. Sur la fonction Forest lisse avec des pauses nettes, la séparation est encore plus perceptible. L'algorithme continue la recherche même lorsqu'il atteint des extrêmes locaux. Sur la fonction discrète Megacity, l'algorithme n'a cédé à l'algorithme RND aléatoire que sur le problème à 500 fonctions.
| AO | Exécutions | Skin | Forest | Megacity (discrète) | Résultat final | ||||||
| 2 paramètres (1 F) | 40 paramètres (20 F) | 1 000 paramètres (500 F) | 2 paramètres (1 F) | 40 paramètres (20 F) | 1 000 paramètres (500 F) | 2 paramètres (1 F) | 40 paramètres (20 F) | 1 000 paramètres (500 F) | |||
| 1 000 | 0,99502 | 0,69826 | 0,50498 | 0,99087 | 0,22374 | 0,08408 | 0,78667 | 0,11667 | 0,04224 | 0,54688 | |
| 10 000 | 0,99599 | 0,86403 | 0,58800 | 0,99302 | 0,65571 | 0,17442 | 0,78667 | 0,26133 | 0,08208 | ||
| 1 000 | 0,98744 | 0,61852 | 0,49408 | 0,89582 | 0,19645 | 0,14042 | 0,77333 | 0,19000 | 0,14283 | 0,51254 | |
| 10 000 | 0,99977 | 0,69448 | 0,50188 | 0,98181 | 0,24433 | 0,14042 | 0,88000 | 0,20133 | 0,14283 | ||
| 1 000 | 0,98436 | 0,72243 | 0,65483 | 0,71122 | 0,15603 | 0,08727 | 0,53333 | 0,08000 | 0,04085 | 0,47695 | |
| 10 000 | 0,99836 | 0,72329 | 0,65483 | 0,97615 | 0,19640 | 0,09219 | 0,82667 | 0,10600 | 0,04085 | ||
| 1 000 | 0,96678 | 0,64727 | 0,57654 | 0,80616 | 0,13388 | 0,06800 | 0,53333 | 0,08067 | 0,04211 | 0,45144 | |
| 10 000 | 0,99505 | 0,64986 | 0,57654 | 0,90401 | 0,18194 | 0,07104 | 0,74667 | 0,10400 | 0,04211 | ||
Conclusions
L'algorithme a beaucoup de paramètres, il est donc possible d'obtenir des résultats encore meilleurs. Possibilité de personnaliser pour des types de tâches spécifiques. Le premier paramètre PheromoneEffect_P affecte directement le taux de convergence. Ceci est particulièrement bon pour les fonctions monotones lisses, par exemple une parabole. La convergence sera de 100%, mais cela contribuera simultanément à rester coincé dans les extrêmes locaux sur les fonctions discrètes si elle est fixée grande.
Le deuxième paramètre PathLengthEffect_P montre le degré de paresse des fourmis. Dans le cas d'une valeur de paramètre élevée, des cibles plus proches seront sélectionnées pour le déplacement. Il est nécessaire d'équilibrer ce paramètre avec le premier afin d'obtenir le meilleur résultat. Ce paramètre est conçu pour fournir un contrepoids au désir de la fourmi d'aller au point où il y a plus de nourriture, au lieu de choisir parfois les cibles les plus proches pour un examen plus détaillé de petites zones, ce qui peut être très utile comme dans l'exemple de la fonction Forest, où le meilleur point peut s'avérer très proche.
La meilleure réalisation est que nous avons réussi à nous débarrasser du principal problème de l'ACO canonique : la capacité à résoudre uniquement des problèmes combinatoires discrets. L'algorithme Colonie de Fourmis peut être utilisé pour former des réseaux de neurones.
Visuellement, l’ensemble des tests est très intéressant à observer du fait d'un certain regroupement. Les fourmis sont concentrées dans les mesures d'une fonction multidimensionnelle mettant en évidence les groupes caractéristiques des extrêmes locaux. Peut-être que cet effet peut être utilisé pour résoudre des problèmes spécifiques, mais cela nécessitera des recherches supplémentaires.
L'algorithme a une propriété intéressante : lors de la résolution d'un problème à 2 variables, la probabilité de rester coincé dans un extrême local est un peu plus élevée que lors de l'optimisation de 40 variables. L'algorithme continue de rechercher des solutions impliquant plusieurs variables. Je suppose que c'est l'effet de l'utilisation d'un vecteur comme moyen de relier toutes les coordonnées de l'espace de recherche. Par exemple, si une fourmi se déplaçait vers un nouveau meilleur endroit, alors toutes les coordonnées changeaient spatialement pour celui-ci, au lieu que certaines coordonnées seulement n’étaient changées séparément.
L'algorithme créé est nouveau et inexploré en détail. Je serai donc reconnaissant si quelqu'un partage les paramètres de l'algorithme, dans lequel les tests afficheront une valeur finale supérieure à 0,6 afin que je puisse mettre à jour les résultats du tableau. Cette demande s'applique aux algorithmes précédemment considérés.
1. L'algorithme est assez rapide.
2. Polyvalence. L'algorithme peut être utilisé dans une variété de problèmes d'optimisation.
3. La capacité de ne pas se concentrer uniquement sur les extrêmes locaux.
4. Assez bonne convergence pour les fonctions lisses et discrètes.
5. Évolutif.
Inconvénients :
1. Peut-être que plus d'itérations sont nécessaires pour la convergence que le même PSO pour les fonctions fluides. Mais cela est partiellement compensé par la possibilité de continuer la recherche même là où le PSO s'est déjà arrêté.
2. Forte influence des paramètres de l'algorithme sur le résultat.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/11602
 Développer un Expert Advisor de trading à partir de zéro (Partie 20) : Nouveau système d'ordre (III)
Développer un Expert Advisor de trading à partir de zéro (Partie 20) : Nouveau système d'ordre (III)
 Apprendre à concevoir un système de trading basé sur la Puissance des Baissiers (Bears Power)
Apprendre à concevoir un système de trading basé sur la Puissance des Baissiers (Bears Power)
 Apprendre à concevoir un système de trading basé sur le Force Index
Apprendre à concevoir un système de trading basé sur le Force Index
- Applications de trading gratuites
- VPS Forex gratuit pendant 24 heures
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation