Algoritmi di ottimizzazione della popolazione: Ottimizzazione della Colonia di formiche (ACO)
Il grande segreto di ogni comportamento è il comportamento sociale...
F. Barlett
Contenuto
1. Introduzione
2. Principi dell’algoritmo
3. Versione modificata
4. Risultati del test
1. Introduzione
Il ricercatore belga Marco Dorigo ha creato un modello matematico che descrive scientificamente il processo di intelligenza collettiva in una colonia di formiche. Lo pubblicò nella sua tesi di dottorato nel 1992 e lo implementò come algoritmo. L'ottimizzazione delle colonie di formiche (ACO) è un metodo di ricerca stocastico basato sulla popolazione per risolvere un'ampia gamma di problemi di ottimizzazione combinatoria. ACO si basa sul concetto di stigmergia. Nel 1959, Pierre-Paul Grasset ha inventato la teoria della stigmergia per spiegare il comportamento della costruzione del nido delle termiti. La stigmergia è composta da due parole greche: stigma - segno ed ergon - azione.
La definizione canonica è un tipo indiretto di interazione tra membri di una popolazione estesa nel tempo attraverso l'interazione con l'ambiente. In altre parole, uno degli agenti lascia una traccia o in qualche modo modifica il luogo, in modo che un altro agente riceva alcune informazioni quando entra nella sua area. Nel caso delle formiche, la stigmergia è costituita dai feromoni. Un esempio di stigmergia è la comunicazione delle formiche nel processo di foraggiamento: le formiche comunicano indirettamente tra loro, lasciando scie di feromoni sul terreno e influenzando così i processi decisionali di altre formiche. Questa semplice forma di comunicazione tra le singole formiche dà origine al complesso comportamento e alle capacità della colonia nel suo insieme.
Le formiche sono insetti sociali, vivono in colonie. Il comportamento delle formiche è controllato dallo scopo della ricerca di cibo. Durante la ricerca, vagano per le loro colonie. La formica salta ripetutamente da un posto all'altro in cerca di cibo e mentre si muove, deposita sul terreno un composto organico chiamato feromone. Pertanto, le formiche comunicano tra loro utilizzando tracce di feromoni.
Quando una formica trova del cibo, ne trasporta tanto quanto ne riesce a trasportare. Al ritorno deposita feromoni lungo il percorso, a seconda della quantità e della qualità del cibo. Di conseguenza, altre formiche possono seguire questo percorso. Più alto è il livello di feromone, maggiore è la probabilità di scegliere questo particolare percorso e più formiche passano su un determinato percorso, più feromone sarà lasciato su questo percorso.
Vediamo il seguente esempio. Supponiamo che ci siano due strade per ottenere cibo dalla colonia. Innanzitutto, non ci sono feromoni sul terreno. Quindi, la probabilità di scegliere questi due percorsi è uguale (50%). Supponiamo che due formiche scelgano due percorsi differenti verso il cibo. Le distanze di questi due percorsi sono diverse. La formica che prende il percorso più breve arriverà al cibo prima dell'altra. Quando trova il cibo, ne prende un po' e torna alla colonia. Mentre ripercorre la sua strada indietro, deposita feromone sul terreno. La formica che prende un percorso più breve raggiungerà la colonia prima.
Quando la terza formica vuole uscire in cerca di cibo, prenderà un percorso che ha una distanza più breve in base al livello di feromone sul terreno. Poiché il percorso più breve ha più feromoni di quello più lungo, la terza formica seguirà il percorso che ha più feromoni. Quando la formica, seguendo il percorso più lungo, è tornata alla colonia, più formiche avevano già passato il percorso con livello più alto di feromoni. Quindi, quando un'altra formica cerca di raggiungere la sua destinazione (cibo) dalla colonia, scoprirà che ogni percorso ha lo stesso livello di feromoni. Quindi ne sceglie uno a caso. Ripetendo questo processo più e più volte, dopo un po', il percorso più breve guadagnerà più feromoni degli altri e la probabilità che le formiche seguano questo percorso sarà maggiore.
L'algoritmo ACO è una sorta di algoritmo di intelligenza dello sciame. Modellando il processo di foraggiamento di una colonia di formiche, viene stabilito il percorso più breve nei vari ambienti utilizzando il meccanismo di trasferimento dati interno della colonia di formiche. Maggiore è la concentrazione del feromone che rimane sul percorso, maggiore è la probabilità che la formica scelga questo percorso. Allo stesso tempo, la concentrazione del feromone diminuisce nel tempo. Perciò, a causa del comportamento della colonia di formiche, le formiche imparano e ottimizzano costantemente attraverso un meccanismo di feedback per determinare il percorso di foraggiamento più breve. L'algoritmo ACO è ampiamente utilizzato nella pianificazione del percorso.
2. Principi dell’algoritmo
In ACO, un insieme di agenti software chiamati formiche artificiali cerca le soluzioni migliori a un dato problema di ottimizzazione. Per applicare ACO, il problema di ottimizzazione viene trasformato nel problema di trovare il percorso migliore su un grafico ponderato. Le formiche artificiali (di seguito denominate formiche) costruiscono gradualmente soluzioni che si muovono lungo il grafico. Il processo di costruzione di una soluzione è stocastico e dipende dal modello di feromone - un insieme di parametri associati ai componenti del grafico (nodi o vertici) i cui valori vengono modificati dalle formiche durante l'esecuzione.
Consideriamo l'algoritmo per il problema del commesso viaggiatore. Abbiamo una serie di luoghi (città) e distanze tra loro. Il problema è trovare un percorso chiuso di lunghezza minima che visiti ogni città una sola volta. Un grafico definito associando un insieme di città a un insieme di vertici del grafico è chiamato grafico di costruzione. Poiché è possibile spostarsi da una data città a qualsiasi altra città, il grafico di costruzione è interamente connesso e il numero di vertici è uguale al numero di città. Impostiamo le lunghezze dei bordi tra i vertici proporzionali alle distanze tra le città rappresentate da quei vertici e associamo i valori dei feromoni e i valori euristici ai bordi del grafico. I valori dei feromoni cambiano in fase di esecuzione e rappresentano l'esperienza cumulativa della colonia di formiche, mentre i valori euristici sono valori dipendenti dal problema.
Le formiche costruiscono soluzioni nel modo seguente. Ogni formica parte da una città selezionata a caso (vertice del grafico di costruzione). Quindi, ad ogni passo della costruzione, si sposta lungo i bordi del grafico. Ogni formica conserva la memoria del proprio percorso, e, nei passaggi successivi, sceglie tra i bordi che non portano a vertici già visitati. La formica ha costruito una soluzione non appena ha visitato tutti i vertici del grafico. Ad ogni fase della costruzione, la formica sceglie probabilisticamente un bordo da seguire tra quelli che conducono a vertici non ancora visitati. La regola probabilistica si basa sui valori dei feromoni e sulle informazioni euristiche: maggiore è il feromone e il valore euristico associati ad un bordo, maggiore è la probabilità che la formica scelga quel particolare bordo. Una volta che tutte le formiche hanno completato il loro viaggio, i feromoni ai bordi vengono aggiornati. Ciascuno dei valori dei feromoni viene inizialmente ridotto di una certa percentuale. Questa procedura viene ripetuta fino a quando viene soddisfatto il criterio di terminazione.
La comunicazione basata sui feromoni è uno dei metodi di comunicazione più efficaci e diffusi in natura. Il feromone è utilizzato da insetti sociali come api, formiche e termiti per la comunicazione tra soggetti. A causa della loro fattibilità, i feromoni artificiali sono stati adottati in sistemi robotici multi-robot e a sciame.
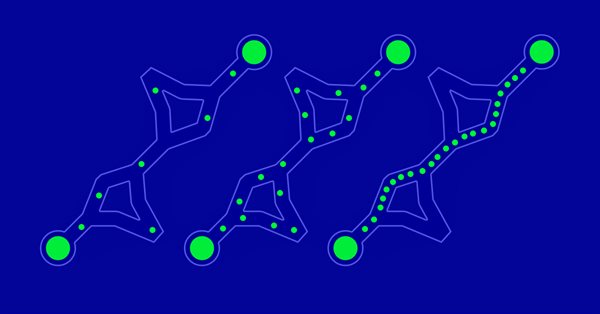
Come facciamo a capire che le nostre formiche hanno davvero trovato la via più breve? C'è un ottimo banco di prova per questo: punti disposti in cerchio. Per loro, il percorso più breve sarà sempre lo stesso - un cerchio.
Il primo algoritmo ACO fu chiamato il sistema delle formiche e mirava a risolvere il problema del commesso viaggiatore, il cui obiettivo è trovare la via più breve in avanti e al ritorno per collegare un certo numero di città. L'algoritmo generale è relativamente semplice e si basa su un insieme di formiche, ognuna delle quali compie uno dei possibili giri di città. Ad ogni tappa, la formica sceglie un percorso da una città all'altra secondo alcune regole:
- Dovrebbe visitare ogni città esattamente una volta;
- È meno probabile che venga selezionata una città lontana (visibilità);
- Più intensa è la scia di feromoni posata sul bordo tra due città, più è probabile che venga scelto questo bordo;
- Completato il suo percorso, la formica deposita più feromoni su tutti i bordi che ha attraversato se il percorso è breve;
- Dopo ogni iterazione, le scie di feromoni evaporano.

Fig. 1. Un esempio di possibili percorsi in cinque punti nodali
3. Versione modificata
Sono note molte delle varianti più popolari degli algoritmi ACO. Consideriamoli:
Sistema di formiche (AS).
Il sistema delle formiche è il primo algoritmo ACO.
Sistema di colonie di formiche (ACS).
Nell'algoritmo del sistema delle colonie di formiche, il sistema di formiche originale è stato modificato in tre aspetti:
1. La selezione dei bordi è orientata allo sfruttamento (cioè, a favore della probabilità di scegliere i bordi più corti con più feromoni);
2. Quando costruiscono una soluzione, le formiche cambiano il livello dei feromoni sui bordi che scelgono applicando una regola locale di aggiornamento dei feromoni;
3. Alla fine di ogni iterazione, solo la formica migliore può aggiornare le tracce applicando la regola modificata dell’aggiornamento globale dei feromoni.
Sistema di formiche d'élite.
In questo algoritmo, la migliore soluzione globale deposita il feromone sulla sua traccia dopo ogni iterazione (anche se la traccia non è stata rivisitata) insieme a tutte le altre formiche. L'obiettivo della strategia d'élite è dirigere la ricerca di tutte le formiche per costruire una soluzione che contenga collegamenti dell'attuale miglior percorso.
Sistema di formiche massimo-minimo (MMAS).
Questo algoritmo controlla il numero massimo e minimo di feromoni su ogni traccia. Solo il miglior tour globale o il miglior tour ripetuto possono aggiungere feromoni alla loro scia. Per evitare il ristagno dell'algoritmo di ricerca, l'intervallo di possibili quantità di feromoni su ciascuna traccia è limitata dall'intervallo [τ max, τ min]. Tutti i bordi sono inizializzati con τ max per velocizzare l'esplorazione della soluzione. Le tracce vengono reinizializzate a τ max quando ci si avvicina alla stagnazione.
Sistema di formiche basato sui ranghi (Asrank).
Tutte le soluzioni sono classificate in base alla loro lunghezza. Solo un numero fisso delle migliori formiche in questa iterazione può aggiornare le proprie sfide. La quantità di feromone depositato viene pesata per ogni soluzione, in modo che le soluzioni con percorsi più brevi depositino più feromone rispetto alle soluzioni con percorsi più lunghi.
Ottimizzazione parallela delle colonie di formiche (PACO).
Sistema di colonie di formiche (ACS) con strategie di comunicazione.
Le formiche artificiali sono divise in diversi gruppi. Vengono proposti sette metodi di comunicazione per aggiornare i livelli di feromoni tra i gruppi dell'ACS che lavorano sul problema del commesso viaggiatore.
Colonia di formiche ortogonali continue (COAC).
Il meccanismo di deposizione dei feromoni COAC consente alle formiche di cercare soluzioni collaborativamente ed efficientemente. Utilizzando il metodo di progettazione ortogonale, le formiche nell'area consentita possono esplorare in modo rapido ed efficiente le aree prescelte con capacità e precisione di ricerca globale maggiore. Il metodo di progettazione ortogonale e il metodo di regolazione del raggio adattivo possono anche essere estesi ad altri algoritmi di ottimizzazione per fornire maggiori vantaggi nella risoluzione di problemi pratici.
Ottimizzazione ricorsiva di una colonia di formiche.
Questa è una forma ricorsiva di una colonia di formiche che divide l'intera area di ricerca in diversi sottodomini e risolve il problema in questi sottodomini. I risultati di tutti i sottodomini vengono confrontati e solo alcuni tra i migliori passano al livello successivo. I sottodomini corrispondenti ai risultati selezionati vengono ulteriormente suddivisi e il processo viene ripetuto fino ad ottenere la precisione desiderata. Questo metodo è stato testato su problemi di inversione geofisica non corretta dimostrandone l'efficacia.
Gli algoritmi della colonia di formiche considerati sopra sono stati originariamente sviluppati per risolvere problemi di ottimizzazione sui grafici. Il problema è integrato in tali algoritmi e le condizioni del problema sono fornite come parametri dell'algoritmo - le coordinate dei nodi del grafico. Perciò, gli algoritmi basati sui principi ACO sono altamente specializzati. Tali algoritmi non sono applicabili per i nostri compiti poiché non utilizziamo coordinate fisse. Potremmo avere qualsiasi coordinata, comprese quelle simili. Per risolvere un'ampia gamma di problemi di ottimizzazione nel campo del trading di strumenti finanziari, incluso l'addestramento delle reti neurali, dobbiamo sviluppare un nuovo algoritmo universale, in modo che possa superare i nostri test speciali, ovvero dovrebbe essere un nuovo tipo di ACO.
Riflettiamo sul concetto di base dell'algoritmo. Proprio come nella versione canonica, avremo una colonia di formiche. Non possiamo contrassegnare i percorsi battuti con i feromoni, possono andare ovunque in uno spazio multidimensionale, memorizzare e salvare percorsi. Con un passo continuo, non sembra appropriato, perché la probabilità di percorrere lo stesso percorso tende a zero. Inoltre, non è affatto necessario memorizzare i nodi, poiché non vi è alcun problema di passaggio sequenziale senza ripetizioni - è necessario eliminare il problema dall'algoritmo. Così, cosa dovremmo fare? In questa fase, non è del tutto chiaro quale direzione prendere nello sviluppo del concetto.
Bene, allora ancora una volta notiamo i punti principali che distinguono il nostro nuovo algoritmo da quello canonico:
1. Non ci sono punti fissi nello spazio.
2. Non è necessario seguire il percorso in un certo ordine.
3. Poiché non ci sono percorsi, non c'è nulla da contrassegnare con i feromoni.
Quindi, scopriamo cosa abbiamo in mente tenendo presente l'idea di una colonia di formiche. Possiamo contrassegnare con i feromoni i punti stessi in cui le formiche hanno camminato, non il percorso in cui hanno viaggiato. Impostiamo il valore della funzione di fitness come il numero di feromoni nella posizione della formica all'iterazione corrente. Quindi le formiche dovranno spostarsi verso le coordinate dove ci sono più feromoni. Ma possiamo incorrere in un problema quando tutte le formiche si spostano semplicemente verso un punto - quello che ha più feromoni. Questa non è necessariamente la migliore soluzione al problema considerando che i punti sono le variabili della funzione ottimizzata. Ricordiamo che nell'ACO classico conta anche la lunghezza del percorso verso il nodo. Più breve è il percorso scelto, meglio è. Quindi dobbiamo calcolare la distanza dalla posizione corrente a dove dovrebbe andare la formica. Il posto successivo è dove si trovano le altre formiche, cioè accettiamo il concetto che le formiche si muovono l'una verso l'altra con una certa casualità.
Che tipo di casualità possiamo aggiungere al movimento?
- Innanzitutto, aggiungere il fattore casuale quando si sceglie la posizione successiva PheromoneEffect_P.
- In secondo luogo, aggiungere un fattore casuale tenendo conto della distanza dalla posizione successiva PathLengthEffect_P (minore è la distanza, migliore è la scelta).
Quindi, abbiamo due criteri per scegliere la posizione successiva - la quantità di feromoni in ogni posizione specifica in cui si trovano le formiche e la distanza tra tutti questi punti a coppie. Tuttavia, anche se lo facciamo utilizzando solo questi due criteri di selezione, le formiche si muoveranno nello spazio lungo i bordi di una figura immaginaria, i cui nodi sono la loro posizione. Quindi, non ci saranno progressi nella ricerca di un posto migliore.
In questo caso, aggiungiamo il raggio di influenza del feromone PheromoneRadius_P (rapporto della distanza tra i punti), entro il quale le formiche possono sentirlo. Quindi le formiche saranno in grado di scivolare oltre il punto in cui si sono spostate. Ciò darà un ulteriore grado di libertà alle formiche quando si muovono nello spazio multidimensionale.
Affinché le formiche possano esplorare nuove aree, devono essere abilitate a deviare dal vettore di direzione lungo una qualsiasi delle coordinate. Introduciamo il rapporto PathDeviation_P , che darà la deviazione dall'incremento a una coordinata specifica. Poiché abbiamo uno spazio multidimensionale, seguendo il vettore di movimento, alcune coordinate possono avere un incremento positivo, mentre altre possono averne uno negativo, e gli incrementi possono avere differenti valori di modulo. Questo rapporto renderà possibile tenere conto di tutto ciò e darà un certo grado di libertà alle formiche nella ricerca del cibo (l'estremo della funzione).
Quindi qual è il vettore di movimento e come misuriamo la distanza che la formica deve percorrere? Per rispondere a queste domande, usiamo l'equazione per calcolare la distanza tra due punti in uno spazio tridimensionale:
![]()
Una rappresentazione visiva del vettore di movimento può essere ottenuta osservando la Figura 2.
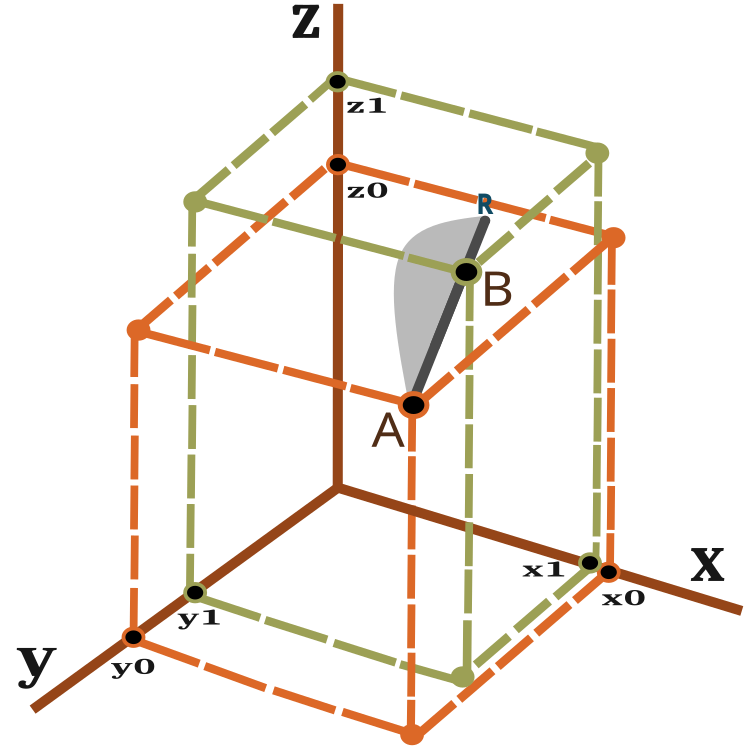
Figura 2. Vettore in movimento della formica
Per gli spazi n-dimensionali, il calcolo è simile.
Una formica in un'iterazione (epoca) si sposta dal punto A al punto B con possibile slittamento al punto R. La distanza dal punto R al punto B dipende dal rapporto PheromoneRadius_P e può essere calcolato come BR = AB x PheromoneRadius_P.
La probabilità di una nuova posizione sulla linea AR è mostrata nella Figura 2 come un'area grigia in modo schematico (non in scala). Pertanto, è più probabile che la nuova posizione della formica tenda al punto B. Il principio dello spostamento di probabilità è stato discusso nell'articolo precedente.
L'algoritmo include i seguenti passaggi ad ogni iterazione:
1) Disposizione casuale delle formiche nello spazio.
2) Determinazione del valore della quantità di feromone (funzione di fitness) per le formiche.
3) Calcolo della distanza da una formica all'altra.
4) La scelta del punto preferito dove si muoverà la formica.
5) Calcolo della probabilità di un punto sul vettore AR.
6) Calcolo delle coordinate del punto ottenuto sul vettore AR.
7) Ripetere dal passaggio 2 finché non viene soddisfatta la condizione di arresto.
Procediamo alla descrizione del codice dell'algoritmo. Prima di tutto, scriviamo una struttura contenente una descrizione della formica, dove:
- c [] - coordinate della formica,
- cLast [] - coordinate precedenti,
- cB [] - migliori coordinate per tutte le iterazioni,
- f - valore attuale del feromone,
- fB - valore massimo del feromone raggiunto in tutte le iterazioni.
Nel costruttore della struttura della formica, inizializziamo il valore di f e fB con il valore minimo possibile che può essere rappresentato dal tipo 'double'.
//—————————————————————————————————————————————————————————————————————————————— struct S_Ants { double cLast []; //last coordinates double c []; //coordinates double cB []; //best coordinates double f; //pheromone of the current coordinates double fB; //pheromone of the best coordinates S_Ants () { f = -DBL_MAX; fB = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Abbiamo bisogno di una struttura il cui array ci consenta di memorizzare le distanze a coppie tra tutte le formiche.
struct S_Paths { double a []; };
Scriverò il nostro algoritmo ACO modificato come una classe, in cui ci sono ancora solo tre metodi pubblici che sono sufficienti e necessari nell'ambito del concetto sviluppato di costruzione di algoritmi di ottimizzazione, considerati negli articoli precedenti - InitAnts (), Preparation () e Dwelling (). Ci sono anche metodi privati GenerateRNDants () e AntsMovement () , così come altri metodi privati che sono già diventati standard per i nostri algoritmi. L'array della struttura ants[] è una colonia di formiche.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACO { public: //---------------------------------------------------------------------------- S_Ants ants []; //ants double rangeMax []; //maximum search range double rangeMin []; //manimum search range double rangeStep []; //step search double cB []; //best coordinates double fB; //pheromone of the best coordinates void InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP); void Preparation (); void Dwelling (); private: //---------------------------------------------------------------------------- S_Paths paths []; int coordinates; //number of coordinates int antHillSize; //ant hill size double goals []; double pheromoneEffect; double pathLengthEffect; double pheromoneRadius; double pathDeviation; bool dwelling; void GenerateRNDants (); void AntsMovement (); double SeInDiSp (double in, double inMin, double inMax, double step); double RNDfromCI (double min, double max); double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
Nel metodo di inizializzazione, assegno i valori iniziali alle variabili e alla dimensione dell'array.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP) { fB = -DBL_MAX; coordinates = coordinatesP; antHillSize = antHillSizeP; pheromoneEffect = pheromoneEffectP; pathLengthEffect = pathLengthEffectP; pheromoneRadius = pheromoneRadiusP; pathDeviation = pathDeviationP; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); dwelling = false; ArrayResize (ants, antHillSize); ArrayResize (paths, antHillSize); for (int i = 0; i < antHillSize; i++) { ArrayResize (ants [i].c, coordinates); ArrayResize (ants [i].cLast, coordinates); ArrayResize (ants [i].cB, coordinates); ArrayResize (paths [i].a, antHillSize); } ArrayResize (cB, coordinates); ArrayResize (goals, antHillSize); } //——————————————————————————————————————————————————————————————————————————————
Il metodo Preparation() viene chiamato per primo a ogni iterazione.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Preparation () { if (!dwelling) { fB = -DBL_MAX; GenerateRNDants (); dwelling = true; } else AntsMovement (); } //——————————————————————————————————————————————————————————————————————————————
Il metodo GenerateRNDants() è responsabile della creazione di una colonia di formiche casuale. Le coordinate della formica sono assegnate casualmente entro i limiti forniti.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::GenerateRNDants () { for (int s = 0; s < antHillSize; s++) { for (int k = 0; k < coordinates; k++) { ants [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); ants [s].c [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); ants [s].cLast [k] = ants [s].c [k]; ants [s].cB [k] = ants [s].c [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Ricordare le coordinate correnti delle formiche nel metodo Dwelling () e aggiornare i valori massimi di feromone ottenuti al momento dell'iterazione corrente.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Dwelling () { for (int i = 0; i < antHillSize; i++) { ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY); //remember the best coordinates for the ant if (ants [i].f > ants [i].fB) { ants [i].fB = ants [i].f; ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY); } //remember the best coordinates for the anthill if (ants [i].f > fB) { fB = ants [i].f; ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Il metodo principale dell'algoritmo AntsMovement() . Esegue le seguenti azioni: calcolo della distanza da una formica all'altra, calcolo della scelta di un punto preferito in cui si sposterà la formica, calcolo della probabilità di un punto sul vettore AR. Calcolo delle coordinate del punto ottenuto sul vettore AR.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::AntsMovement () { double rndPh; double rndPt; double summCoordinates = 0.0; double scores []; ArrayResize (scores, antHillSize); double maxPh = -DBL_MAX; double minPh = DBL_MAX; double maxPt = -DBL_MAX; double minPt = DBL_MAX; double goal; double goalBest = -DBL_MAX; int goalInd = 0; //measure the distance between all the ants----------------------------------- for (int i = 0; i < antHillSize; i++) { for (int k = 0; k < antHillSize; k++) { if (i == k) { paths [i].a [k] = DBL_MAX; continue; } for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0); paths [i].a [k] = pow (summCoordinates, 0.5); if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k]; if (minPt > paths [i].a [k]) minPt = paths [i].a [k]; } } //---------------------------------------------------------------------------- for (int i = 0; i < antHillSize; i++) { maxPh = -DBL_MAX; minPh = DBL_MAX; for (int k = 0; k < antHillSize; k++) { if (i != k) { if (maxPh < ants [k].f) maxPh = ants [k].f; if (minPh > ants [k].f) minPh = ants [k].f; } } goalBest = -DBL_MAX; goalInd = 0; for (int k = 0; k < antHillSize; k++) { if (i != k) { rndPh = RNDfromCI (0.0, pheromoneEffect); rndPt = RNDfromCI (0.0, pathLengthEffect); goal = Scale (ants [k].f, minPh, maxPh, 0.0, 1.0, false) * rndPh * Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true) * rndPt; if (goalBest < goal) { goalBest = goal; goalInd = k; } } } double wayToGoal = paths [i].a [goalInd]; double radiusNearGoal = wayToGoal * pheromoneRadius; double endWay = wayToGoal + radiusNearGoal; double x = RNDfromCI (-1.0, 1.0); double y = x * x; if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay, false); else y = Scale (y, 0.0, 1.0, 0.0, wayToGoal, true); for (int j = 0; j < coordinates; j++) { double incrementFactor = y / wayToGoal; double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j]; ants [i].c [j] = ants [i].cLast [j] + (coordDistance * incrementFactor); double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation; ants [i].c [j] += w; ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Vale la pena prestare attenzione alla funzione di ridimensionamento di un numero da un intervallo numerico ad un altro. L'ho già considerato in articoli precedenti. Questa volta amplierò la sua funzionalità. L'input revers viene utilizzato per modificare la direzione di ridimensionamento come mostrato nella figura seguente.
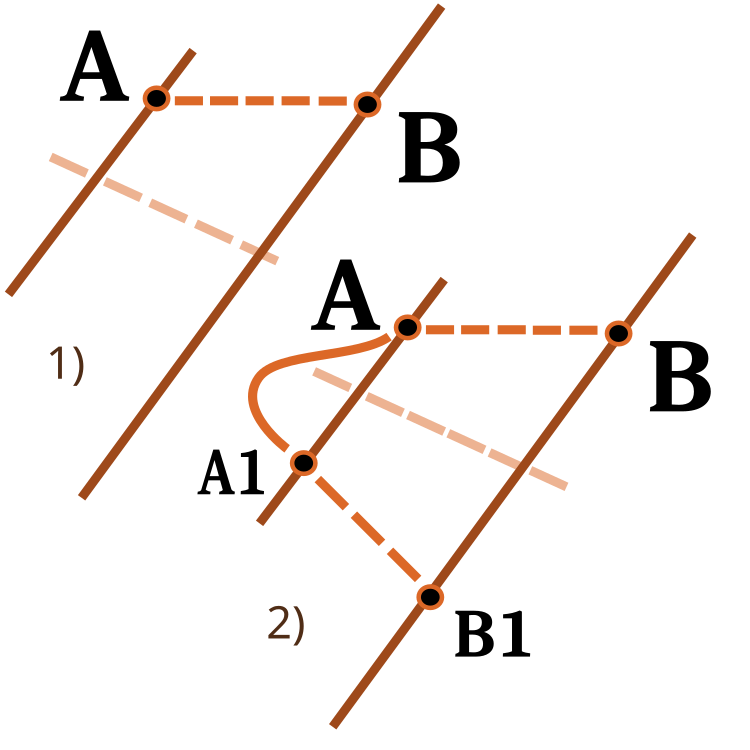
Fig. 3. Ridimensionamento di un numero da un intervallo numerico a un altro.
1) Ridimensionamento diretto; 2) Ridimensionamento inverso
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return revers ? OutMAX : OutMIN; if (In > InMAX) return revers ? OutMIN : OutMAX; double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); if (!revers) return res; else return OutMAX - res; } } //——————————————————————————————————————————————————————————————————————————————
4. Risultati del test
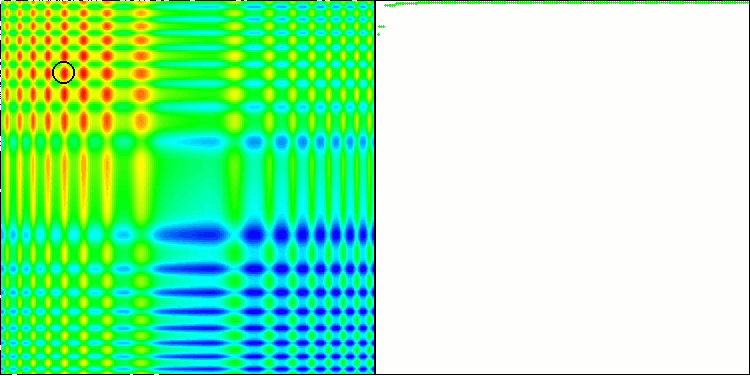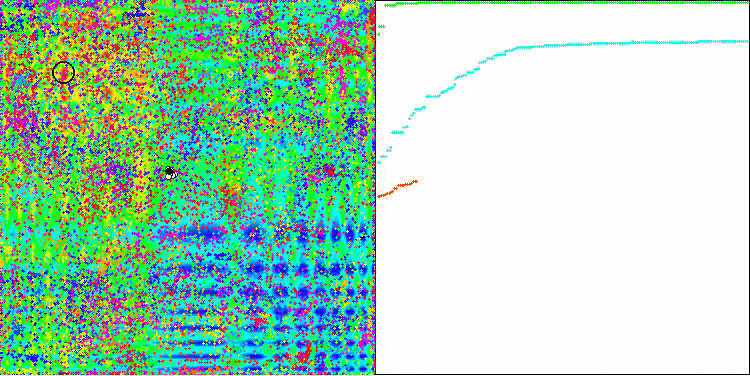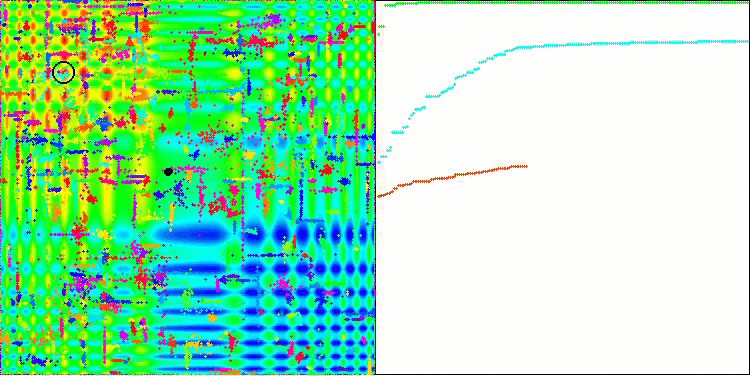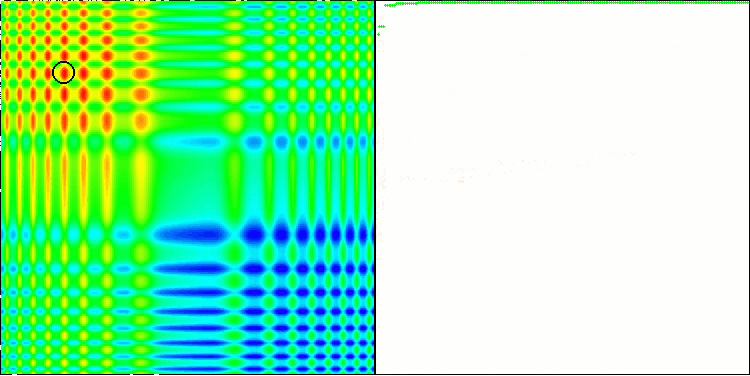
ACO sulla funzione test Skin
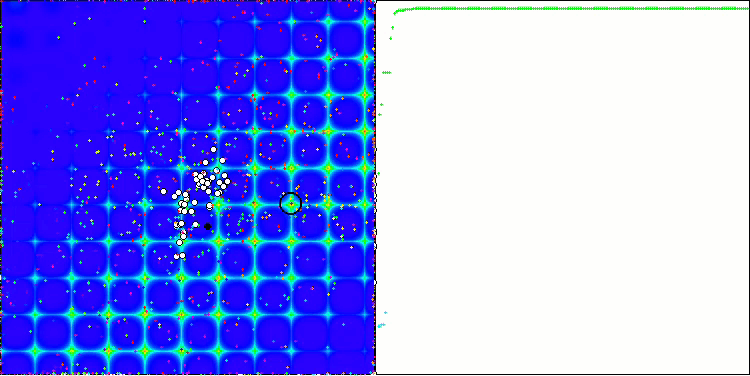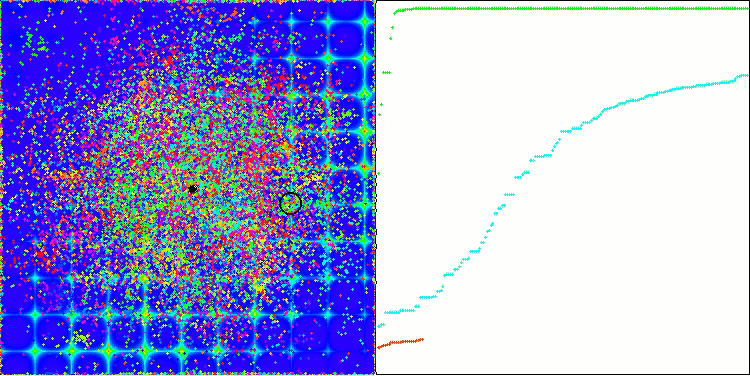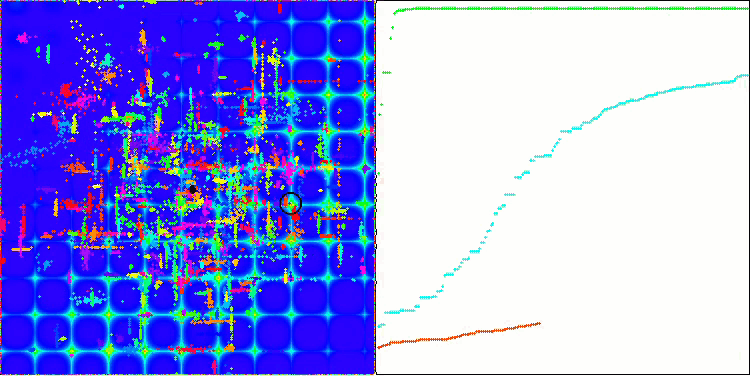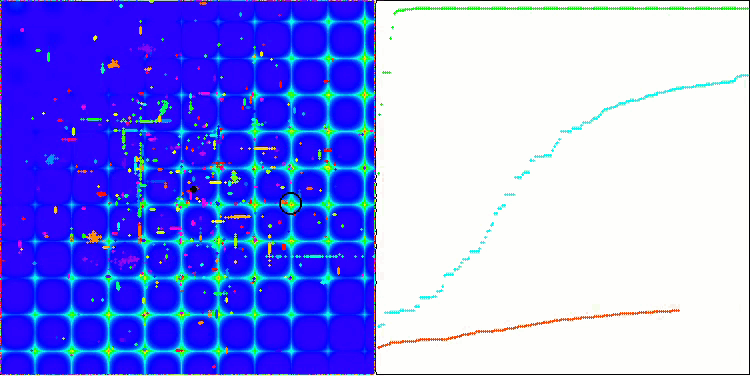
ACO sulla funzione di test Forest
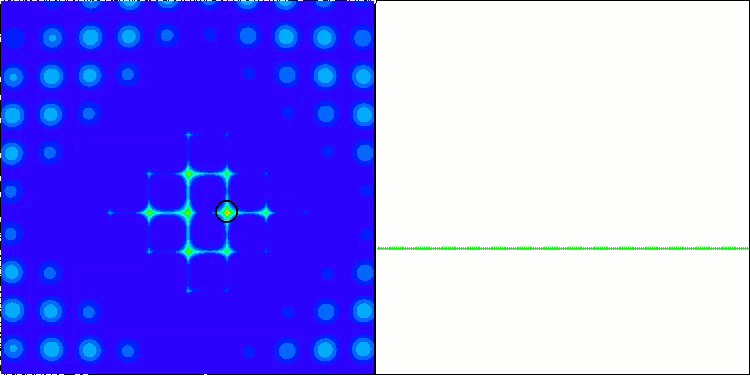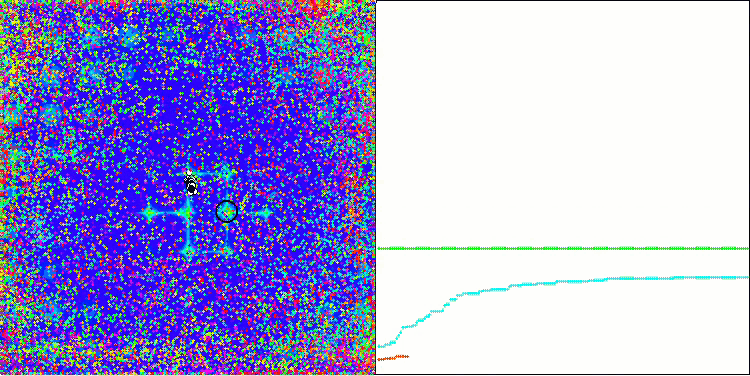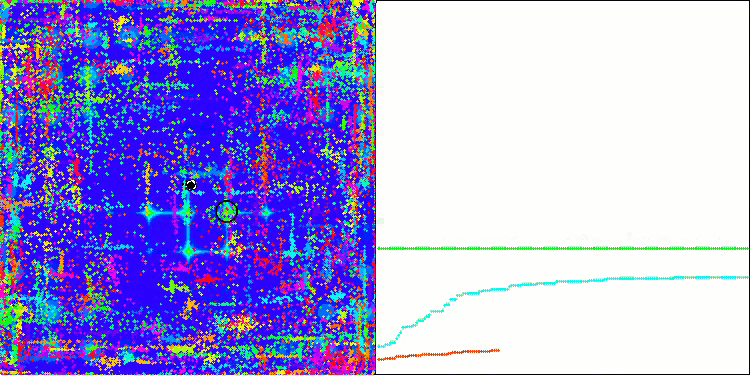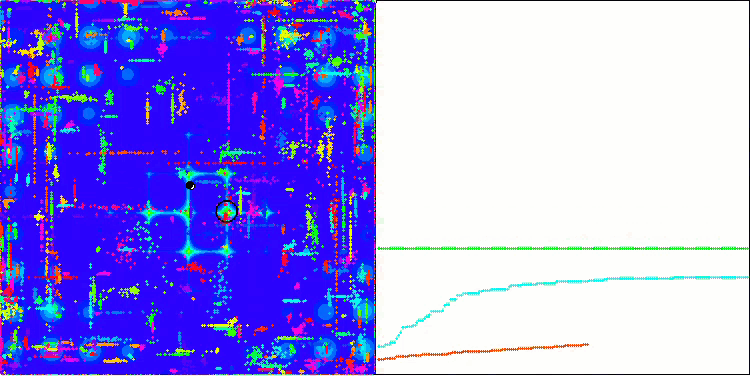
ACO sulla funzione di test Megacity
Quindi, è tempo di conclusioni. Da un lato, l'algoritmo convenzionale Ant Colony non è applicabile ai problemi di ottimizzazione per il trading di strumenti finanziari. Tuttavia, nel tentativo di evitare i limiti della versione convenzionale, abbiamo assistito all'emergere di un concetto completamente nuovo dell'algoritmo Ant Colony che consente un ulteriore sviluppo di ACO. Tale algoritmo può già essere applicato a una vasta gamma di problemi, incluso il problema del commesso viaggiatore.
Inoltre, ora abbiamo un nuovo leader della classifica. Consideriamo i risultati in modo più dettagliato. Innanzitutto, presta attenzione ai risultati del banco di prova:
2022.10.27 16:46:28.678 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) 1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) Score1: 0.99502; Score2: 0.99599 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) 20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) Score1: 0.69826; Score2: 0.86403 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) 500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) Score1: 0.50498; Score2: 0.58800 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) 1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) Score1: 0.99087; Score2: 0.99302 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) 20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) Score1: 0.22374; Score2: 0.65571 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) 500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) Score1: 0.08408; Score2: 0.17442 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) 1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) Score1: 0.78667; Score2: 0.78667 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) 20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) Score1: 0.11667; Score2: 0.26133 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) 500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) Score1: 0.04224; Score2: 0.08208 2022.10.27 16:49:41.075 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) All score for C_AO_ACO: 0.5468768583006471
L'algoritmo ha funzionato bene sulla funzione regolare Skin, dimostrando un'eccellente convergenza e buone capacità di ridimensionamento, risultando particolarmente avanti nei test di 20 e 500 funzioni. Sulla funzione regolare Forest con interruzioni nette, la separazione è ancora più evidente. L'algoritmo continua la ricerca anche quando raggiunge gli estremi locali. Sulla funzione discreta Megacity, l'algoritmo ha ceduto all'algoritmo RND casuale solo sul problema con 500 funzioni.
| AO | Cicli | Skin | Forest | Megacity (discreto) | Risultato finale | ||||||
| 2 parametri (1 F) | 40 parametri (20 F) | 1000 parametri (500 F) | 2 parametri (1 F) | 40 parametri (20 F) | 1000 parametri (500 F) | 2 parametri (1 F) | 40 parametri (20 F) | 1000 parametri (500 F) | |||
| 1000 | 0.99502 | 0,69826 | 0,50498 | 0,99087 | 0.22374 | 0.08408 | 0.78667 | 0.11667 | 0.04224 | 0,54688 | |
| 10.000 | 0,99599 | 0.86403 | 0.58800 | 0.99302 | 0.65571 | 0.17442 | 0.78667 | 0.26133 | 0.08208 | ||
| 1000 | 0,98744 | 0,61852 | 0.49408 | 0,89582 | 0.19645 | 0.14042 | 0,77333 | 0.19000 | 0.14283 | 0,51254 | |
| 10.000 | 0,99977 | 0,69448 | 0,50188 | 0.98181 | 0.24433 | 0.14042 | 0,88000 | 0.20133 | 0.14283 | ||
| 1000 | 0,98436 | 0.72243 | 0,65483 | 0.71122 | 0.15603 | 0,08727 | 0,53333 | 0,08000 | 0.04085 | 0,47695 | |
| 10.000 | 0,99836 | 0,72329 | 0,65483 | 0,97615 | 0.19640 | 0.09219 | 0,82667 | 0,10600 | 0.04085 | ||
| 1000 | 0,96678 | 0,64727 | 0,57654 | 0.80616 | 0.13388 | 0,06800 | 0,53333 | 0,08067 | 0.04211 | 0.45144 | |
| 10.000 | 0,99505 | 0,64986 | 0,57654 | 0.90401 | 0.18194 | 0.07104 | 0,74667 | 0.10400 | 0.04211 | ||
Conclusioni
L'algoritmo ha molte impostazioni, così è possibile ottenere risultati ancora migliori. Possibilità di personalizzare per specifici tipi di attività. Il primo parametro PheromoneEffect_P influenza direttamente il tasso di convergenza. Ciò è particolarmente utile per le funzioni monotone uniformi, ad esempio una parabola. La convergenza sarà del 100%, ma questo contribuirà contemporaneamente a rimanere bloccati negli estremi locali su funzioni discrete se impostato su grande.
Il secondo parametro PathLengthEffect_P mostra il grado di pigrizia delle formiche. In caso di un valore di parametro elevato, verranno selezionati obiettivi più vicini per lo spostamento. È necessario bilanciare questo parametro con il primo per ottenere il miglior risultato. Questo parametro ha lo scopo di fornire un contrappeso al desiderio della formica di andare nel punto dove c'è più cibo, scegliendo invece a volte gli obiettivi più vicini per un esame più approfondito di piccole aree, che può essere molto utile come nell'esempio della funzione Forest, dove il punto migliore può risultare essere molto vicino.
Il risultato più importante è che siamo riusciti a liberarci del problema principale dell'ACO canonico: la capacità di risolvere solo problemi combinatori discreti. Ora l'algoritmo Ant Colony può essere utilizzato per addestrare reti neurali.
Visivamente il banco prova è molto interessante da osservare per via di un certo raggruppamento, le formiche si concentrano nelle misure di una funzione multidimensionale evidenziando in un certo modo i caratteristici gruppi di estremi locali. Forse questo effetto può essere utilizzato per risolvere problemi specifici, ma ciò richiederà ulteriori ricerche.
L'algoritmo ha una proprietà interessante: quando si risolve un problema con due variabili, la probabilità di rimanere bloccati in un estremo locale è leggermente superiore rispetto a quando si ottimizzano 40 variabili. L'algoritmo continua a cercare soluzioni che coinvolgono molteplici variabili. Presumo che questo sia l'effetto dell'utilizzo di un vettore come mezzo di collegamento per tutte le coordinate dello spazio di ricerca. Ad esempio, se una formica si è spostata in un altro posto migliore, tutte le coordinate vengono modificate spazialmente in meglio, piuttosto che avere alcune coordinate che cambiano separatamente.
L'algoritmo creato è nuovo e inesplorato nel dettaglio, quindi sarò grato se qualcuno condivide le impostazioni dell'algoritmo, in cui il banco di prova mostrerà un valore finale maggiore di 0,6 in modo da poter aggiornare i risultati della tabella. Questo invito si applica agli algoritmi considerati in precedenza.
1. L'algoritmo è abbastanza veloce.
2. Versatilità. L'algoritmo può essere utilizzato in una varietà di problemi di ottimizzazione.
3. La capacità di non concentrarsi solo sugli estremi locali.
4. Convergenza abbastanza buona per entrambe le funzioni regolari e discrete.
5. Scalabile.
Contro:
1. Forse sono necessarie più iterazioni per la convergenza rispetto allo stesso PSO per funzioni regolari, ma ciò è parzialmente compensato dalla possibilità di continuare la ricerca anche dove PSO si è già fermato.
2. Forte influenza dei parametri dell'algoritmo sul risultato.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/11602
 Impara come progettare un sistema di trading tramite Bear’s Power
Impara come progettare un sistema di trading tramite Bear’s Power
 Sviluppare un Expert Advisor per il trading da zero (Parte 20): Nuovo sistema di ordini (III)
Sviluppare un Expert Advisor per il trading da zero (Parte 20): Nuovo sistema di ordini (III)
 Impara come progettare un sistema di trading tramite Force Index
Impara come progettare un sistema di trading tramite Force Index
- App di trading gratuite
- VPS Forex gratuito per 24 ore
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso