Previsão usando modelos ARIMA em MQL5

Introdução

O artigo Implementando um algoritmo de treinamento ARIMA em MQL5 descreve a classe CArima para a construção de modelos ARIMA. Embora seja tecnicamente possível usar a classe como está para aplicar um modelo e fazer previsões, não é intuitivo. Neste artigo, abordaremos essa limitação e estenderemos a classe para permitir métodos mais fáceis de usar a fim de aplicar modelos e fazer previsões. Discutiremos alguns dos desafios relacionados à implementação de previsões, bem como algumas novas funcionalidades adicionadas à classe. Para concluir, usaremos a classe completa para construir um modelo, usá-lo para prever os preços Forex aplicando-o a um Expert Advisor e indicador.

Série de parâmetros de entrada

É bem conhecido que os modelos ARIMA dependem de dependências temporais em um conjunto de dados. É por esse motivo que, para fazer uma ou mais previsões, é necessário alimentar o modelo com uma série de dados de entrada. A especificação do modelo determina o tamanho mínimo da série de entrada. Sabendo disso, torna-se óbvio que, se a série de entrada for incorreta, não será possível fazer previsões ou, pelo menos, as previsões não serão reflexo do modelo aplicado. Diferentes tipos de modelos ARIMA têm requisitos diferentes quanto ao tamanho da série de entrada, além da ordem do modelo.

A implementação de previsões para modelos autorregressivos puros é trivial, pois tudo o que é necessário é uma entrada igual ao maior atraso do modelo. Modelos mistos que utilizam termos de média móvel criam problemas ao fazer previsões. Ainda não temos nenhuma série de bugs ou inovações reais. Para superar isso, primeiro devemos decidir como serão calculados os valores de erro iniciais.

Esse processo envolve, em primeiro lugar, o uso de quaisquer parâmetros de modelo disponíveis para obter o estado inicial do modelo, o que exclui todos os termos de média móvel, pois eles são assumidos como 0 nesta fase. Os valores conhecidos da série são então usados ​​para calcular os valores de erro iniciais, percorrendo a série de previsões redundantes. Estas previsões iniciais são redundantes porque não terão nada a ver com as previsões finais nas quais estamos interessados. Isso, obviamente, aumenta as demandas quanto ao número de entradas necessárias para a previsão. O importante aqui é estimar quantos ciclos de previsão redundantes devem ser realizados para obter valores adequados da série de erros a fim de fazer previsões válidas.

Ainda há mais a considerar em termos do número de entradas do modelo. A classe CArima tem a capacidade de especificar modelos com defasagens não contíguas. Isso aumenta ainda mais as demandas quanto ao número de entradas necessárias. Neste caso, a maior defasagem de qualquer tipo (AR/MA) aumentará os requisitos de tamanho de entrada. Considere um modelo definido pela função:                                                                                             

price(t) = constant_term + AR*price(t-4)

Esta função especifica um modelo com um único termo AR em uma defasagem de quatro. Isso significa que o preço atual é parcialmente determinado pelo valor quatro intervalos de tempo antes. Embora precisemos apenas de um desses valores, devemos lembrar de preservar as relações de tempo dos dados de entrada. Assim, em vez de apenas um requisito de entrada, na verdade precisamos de quatro, além de outros requisitos do modelo. O determinante final do tamanho da série de entradas depende se é necessária alguma diferenciação.

Levando em conta a diferenciação

Os requisitos de diferenciação aumentam a quantidade de dados necessários, não devido a factores envolvidos no cálculo do(s) valor(es) previsto(s), mas porque a diferenciação leva a uma perda de informações. Ao criar uma série diferenciada, ela sempre será uma unidade menor em comprimento em relação à série original. Esta série mais curta será eventualmente passada como entrada para o modelo. Desse modo, em geral, entradas extras são necessárias para compensar aquelas que correspondem à ordem de diferenciação especificada pelo modelo.

Além do impacto que a diferenciação tem no tamanho das entradas, ela também afeta as previsões finais, pois estarão no domínio diferenciado. As previsões, juntamente com a série de entradas fornecida, devem ser combinadas e integradas para retornar valores combinados ao domínio original.

Previsão a longo prazo

Às vezes, os usuários podem estar interessados em prever vários intervalos de tempo no futuro com base em um único conjunto de entradas. Embora isso não seja recomendado, é um método que vale a pena explorar. Ao fazer previsões de longo prazo, devemos nos lembrar de certos axiomas. Primeiro, quanto mais avançamos, eventualmente temos que usar previsões de intervalos de tempo anteriores como entradas para quaisquer termos autorregressivos. Uma vez que ultrapassamos os valores conhecidos da série, que são usados como entradas iniciais, não temos mais meios para calcular os valores de erro, uma vez que os valores futuros reais são desconhecidos. Consequentemente, os termos de média móvel para esses intervalos de tempo serão e só podem ser assumidos como zero. Isso faz com que a série prevista degenere em um processo autorregressivo puro, se especificado, ou em um processo definido apenas pelo termo constante. Fazer várias previsões a longo prazo deve ser feito com consciência das limitações inerentes.

Adições à classe CArima

A primeira alteração feita na classe é em seu método pai CPowellsMethod. O método Optimize() agora está protegido por um modificador de acesso e não pode ser acessado de fora da classe. Naturalmente, esta alteração também se aplica ao CArima. Devido a essa modificação, o nome do arquivo de inclusão que contém a classe CPowellsMethod é alterado para apenas Powells.mqh.

//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
   double            P[],Xi[];
   double            Pcom[],Xicom[],Xt[];
   double            Pt[],Ptt[],Xit[];
   int               N;
   double            Fret;
   int               Iter;
   int               ItMaxPowell;
   double            FtolPowell;
   int               ItMaxBrent;
   double            FtolBrent;
   int               MaxIterFlag;
   int               Optimize(double &p[],int n=0);
public:
   void              PowellsMethod(void);
   void              SetItMaxPowell(int n)           { ItMaxPowell=n; }
   void              SetFtolPowell(double er)        { FtolPowell=er; }
   void              SetItMaxBrent(int n)            { ItMaxBrent=n;  }
   void              SetFtolBrent(double er)         { FtolBrent=er;  }
   double            GetFret(void)                   { return(Fret);  }
   int               GetIter(void)                   { return(Iter);  }
private:
   void              powell(void);
   void              linmin(void);
   void              mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
   double            brent(double ax,double bx,double cx,double &xmin);
   double            f1dim(double x);
   virtual double    func(const double &p[]) { return(0); }
  };

Uma característica significativa adicionada à classe é a capacidade de salvar e carregar modelos. Isso permite treinar e salvar um modelo para uso posterior ou inclusão em qualquer outro programa MQL5.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::SaveModel(const string model_name)
  {
   uint model_order[]= {m_const,m_ar_order,m_diff_order,m_ma_order};

   CFileBin file;
   ResetLastError();
   if(!file.Open("models\\"+model_name+".model",FILE_WRITE|FILE_COMMON))
     {
      Print("Failed to save model.Error: ",GetLastError());
      return false;
     }

   m_modelname=(m_modelname=="")?model_name:m_modelname;

   long written=0;

   written = file.WriteIntegerArray(model_order);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(m_ar_order)
     {
      written = file.WriteIntegerArray(m_arlags);

      if(!written)
        {
         Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
         return false;
        }
     }

   if(m_ma_order)
     {
      written = file.WriteIntegerArray(m_malags);

      if(!written)
        {
         Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
         return false;
        }
     }

   written = file.WriteDoubleArray(m_model);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   written = file.WriteDouble(m_sse);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }


   file.Close();

   return true;

  }

O método SaveModel permite salvar modelos e requer uma inserção de uma string que será o novo nome do modelo. O método em si é gravado em um arquivo binário .model armazenado no diretório de modelos da pasta de arquivos comuns (Terminal\Common\Files\models). O arquivo salvo contém a ordem do modelo, bem como seus parâmetros, se tiver sido treinado, incluindo o valor da soma dos erros quadrados (sse).

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::LoadModel(const string model_name)
  {
   int found=StringFind(model_name,".model");

   if(found>=0)
      m_modelname=StringSubstr(model_name,0,found);
   else
      m_modelname=model_name;

   if(StringFind(m_modelname,"\\")>=0)
      return false;

   string filename="models\\"+m_modelname+".model";

   if(!FileIsExist(filename,FILE_COMMON))
     {
      Print("Failed to find model, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   CFileBin file;
   ResetLastError();
   if(file.Open(filename,FILE_READ|FILE_COMMON)<0)
     {
      Print("Failed open operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   uint model_order[];


   file.Seek(0,SEEK_SET);

   if(!file.ReadIntegerArray(model_order,0,4))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   m_const=bool(model_order[0]);
   m_ar_order=model_order[1];
   m_diff_order=model_order[2];
   m_ma_order=model_order[3];

   file.Seek(sizeof(uint)*4,SEEK_SET);

   if(m_ar_order && !file.ReadIntegerArray(m_arlags,0,m_ar_order))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(!m_ar_order)
      ArrayFree(m_arlags);



   if(m_ar_order)
      file.Seek(sizeof(uint)*(4+m_ar_order),SEEK_SET);


   if(m_ma_order && !file.ReadIntegerArray(m_malags,0,m_ma_order))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   ArrayPrint(m_malags);

   if(!m_ma_order)
      ArrayFree(m_malags);


   if(m_ar_order || m_ma_order)
      file.Seek(sizeof(uint)*(4+m_ar_order+m_ma_order),SEEK_SET);



   if(!file.ReadDoubleArray(m_model,0,m_ma_order+m_ar_order+1))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   file.Seek(sizeof(uint)*(4+m_ar_order+m_ma_order) + sizeof(double)*ArraySize(m_model),SEEK_SET);

   if(!file.ReadDouble(m_sse))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(m_model[1])
      m_istrained=true;
   else
      m_istrained=false;

   ZeroMemory(m_differenced);
   ZeroMemory(m_leads);
   ZeroMemory(m_innovation);

   m_insize=0;

   return true;
  }

O método LoadModel precisa do nome do modelo e lê todos os atributos de um modelo previamente salvo. Ambos os métodos retornam verdadeiro ou falso, e mensagens de erro úteis são gravadas no log do terminal.

string            GetModelName(void)                      { return m_modelname;}

O método GetModelName() retorna o nome do modelo, e retornará uma string vazia se o modelo nunca tiver sido salvo, caso contrário, retornará o nome definido ao salvar o modelo.

//+------------------------------------------------------------------+
//| calculate the bayesian information criterion                     |
//+------------------------------------------------------------------+
double CArima::BIC(void)
  {
   if(!m_istrained||!m_sse)
     {
      Print(m_modelname," Model not trained. Train the model first to calculate the BIC.");
      return 0;
     }

   if(!m_differenced.Size())
     {
      Print("To calculate the BIC, supply a training data set");
      return 0;
     }
   uint n = m_differenced.Size();
   uint k = m_ar_order+m_ma_order+m_diff_order+uint(m_const);

   return((n*MathLog(m_sse/n)) + (k*MathLog(n)));

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CArima::AIC(void)
  {
   if(!m_istrained||!m_sse)
     {
      Print(m_modelname," Model not trained. Train the model first to calculate the AIC.");
      return 0;
     }

   if(!m_differenced.Size())
     {
      Print("To calculate the AIC, supply a training data set");
      return 0;
     }

   uint n = m_differenced.Size();
   uint k = m_ar_order+m_ma_order+m_diff_order+uint(m_const);

   return((2.0*k)+(double(n)*MathLog(m_sse/double(n))));
  }
//+------------------------------------------------------------------+

Também são novos os métodos BIC e AIC. O método BIC retorna o critério de informação bayesiano com base no valor sse de um modelo. O método AIC calcula o critério de informação de Akaike e funciona de maneira semelhante à função BIC. O Critério de Informação Bayesiano (BIC) e o Critério de Informação de Akaike (AIC) são medidas estatísticas usadas para seleção de modelos. Ambos os critérios visam equilibrar a adequação de um modelo com sua complexidade, de modo que modelos mais simples sejam preferidos se ajustarem aos dados quase tão bem quanto modelos mais complexos.

BIC e AIC diferem na forma como equilibram qualidade de ajuste e complexidade. O BIC dá mais peso à simplicidade do modelo do que o AIC, o que significa que ele favorece modelos ainda mais simples em relação ao AIC. Por outro lado, o AIC é mais propenso a selecionar modelos mais complexos do que o BIC. Em termos simples, o BIC e o AIC nos permitem comparar diferentes modelos e escolher aquele que melhor se ajusta aos nossos dados, levando em consideração a complexidade do modelo. Ao escolher um modelo mais simples, podemos evitar o overfitting, que ocorre quando um modelo é muito complexo e se ajusta muito bem aos dados, tornando-o menos útil para prever novas observações.

Ambos retornam 0 em caso de erro e devem ser chamados imediatamente após um modelo ter sido treinado enquanto os dados de treinamento ainda estão carregados. Quando o modelo treinado for inicializado, os dados utilizados para treinamento não estarão disponíveis, portanto nem o BIC nem o AIC poderão ser calculados.

uint              GetMinModelInputs(void)                 { return(m_diff_order + GetMaxArLag() + (GetMaxMaLag()*m_infactor));}

Agora também é possível consultar o número mínimo de entradas exigidas pelo modelo. Isso é feito usando o método GetMinModelInputs().

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CArima::Summary(void)
  {

   string print = m_modelname+" Arima("+IntegerToString(m_ar_order)+","+IntegerToString(m_diff_order)+","+IntegerToString(m_ma_order)+")\n";
   print+= "SSE : "+string(m_sse);

   int k=0;
   if(m_const)
      print+="\nConstant: "+string(m_model[k++]);
   else
      k++;
   for(uint i=0; i<m_ar_order; i++)
      print+="\nAR coefficient at lag "+IntegerToString(m_arlags[i])+": "+string(m_model[k++]);
   for(uint j=0; j<m_ma_order; j++)
      print+="\nMA coefficient at lag "+IntegerToString(m_malags[j])+": "+string(m_model[k++]);

   Print(print);

   return;

  }

Finalmente, a chamada para Summary() grava os atributos do modelo no terminal, não retornando mais uma string.

Implementação de previsões

   bool              Predict(const uint num_pred,double &predictions[]);
   bool              Predict(const uint num_pred,double &in_raw[], double &predictions[]);
   bool              SaveModel(const string model_name);
   bool              LoadModel(const string model_name);
   double            BIC(void);
   double            AIC(void);

A aplicação de um modelo para fazer previsões é implementada por meio de dois métodos sobrecarregados chamados Predict(). Ambos recebem como entrada dois parâmetros de entrada idênticos:

• num_pred — valor inteiro especificando o número de previsões desejadas.

• predictions — array duplo exibindo valores previstos.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::Predict(const uint num_pred,double &predictions[])
  {
   if(!num_pred)
     {
      Print("Invalid number of predictions");
      return false;
     }

   if(!m_istrained || !m_insize)
     {
      ZeroMemory(predictions);
      if(m_istrained)
         Print("Model not trained");
      else
         Print("No input data available to make predictions");
      return false;
     }

   ArrayResize(m_differenced,ArraySize(m_differenced)+num_pred,num_pred);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   evaluate(num_pred);

   if(m_diff_order)
     {
      double raw[];
      integrate(m_differenced,m_leads,raw);
      ArrayPrint(raw,_Digits,NULL,m_insize-5);
      ArrayCopy(predictions,raw,0,m_insize+m_diff_order);
      ArrayFree(raw);
     }
   else
      ArrayCopy(predictions,m_differenced,0,m_insize);

   return true;
  }

Os métodos Predict diferem em termos do número de parâmetros de função. O primeiro método, que requer dois parâmetros, é usado para fazer previsões com base nos dados de treinamento usados para derivar os coeficientes ótimos do modelo.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::Predict(const uint num_pred,double &in_raw[],double &predictions[])
  {
   if(!num_pred)
     {
      Print("Invalid number of predictions");
      return false;
     }

   if(!m_istrained)
     {
      ZeroMemory(predictions);
      Print("Model not trained");
      return false;
     }

   int numofinputs=0;

   if(m_ar_order)
      numofinputs+=(int)GetMaxArLag();
   if(m_ma_order)
      numofinputs+=int(GetMaxMaLag()*m_infactor);
   if(m_diff_order)
      numofinputs+=(int)m_diff_order;

   if(in_raw.Size()<(uint)numofinputs)
     {
      ZeroMemory(predictions);
      Print("Input dataset size inadequate. Size required: ",numofinputs);
      return false;
     }

   ZeroMemory(m_differenced);

   if(m_diff_order)
     {
      difference(m_diff_order,in_raw,m_differenced,m_leads);
      m_insize=m_differenced.Size();
     }
   else
     {
      m_insize=in_raw.Size();
      ArrayCopy(m_differenced,in_raw);
     }


   if(m_differenced.Size()!=(m_insize+num_pred))
      ArrayResize(m_differenced,m_insize+num_pred,num_pred);

   ArrayFill(m_differenced,m_insize,num_pred,0.0);

   if(m_innovation.Size()!=m_insize+num_pred)
      ArrayResize(m_innovation,ArraySize(m_differenced));

   ArrayInitialize(m_innovation,0.0);

   evaluate(num_pred);

   if(m_diff_order)
     {
      double raw[];
      integrate(m_differenced,m_leads,raw);
      ArrayCopy(predictions,raw,0,m_insize+m_diff_order);
      ArrayFree(raw);
     }
   else
      ArrayCopy(predictions,m_differenced,0,m_insize);

   return true;

  }

O segundo método Predict exige um terceiro parâmetro de entrada, um array que deve conter a série de entradas a serem usadas para calcular as previsões. Ambos os métodos retornam um valor booleano e também fazem uso da função privada evaluate.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CArima::evaluate(const uint num_p)
  {

   double pred=0;
   uint start_shift=(m_ma_order)?((!m_innovation[m_insize-1])?m_insize-(GetMaxMaLag()*m_infactor):m_insize):m_insize;
   uint d_size=(uint)ArraySize(m_differenced);

   int p_shift;

   for(uint i=start_shift; i<d_size; i++)
     {
      p_shift=0;
      pred=0;
      if(i>=m_insize)
         m_innovation[i]=0.0;
      if(m_const)
         pred+=m_model[p_shift++];
      for(uint j=0; j<m_ar_order; j++)
         pred+=m_model[p_shift++]*m_differenced[i-m_arlags[j]];
      for(uint k=0; i>=GetMaxMaLag() && k<m_ma_order; k++)
         pred+=m_model[p_shift++]*m_innovation[i-m_malags[k]];
      if(i>=m_insize)
         m_differenced[i]=pred;
      if(i<m_insize)
         m_innovation[i]=pred-m_differenced[i];
     }

   return;
  }

O método evaluate() é semelhante ao método func() com algumas pequenas diferenças. Ele recebe como único argumento o número desejado de previsões e varre até cinco arrays, dependendo da especificação do modelo. Ele calcula novas previsões e adiciona novos valores à série de erros (inovação) conforme necessário. Uma vez concluído, os valores previstos são extraídos e copiados para o array de destino fornecido ao método Predict(). Os métodos Predict retornam verdadeiro em caso de sucesso e falso se houver qualquer erro.

Usando a classe

Para demonstrar o uso da classe CArima modificada, construiremos um script que treina alguns modelos e salva o melhor deles, realizando uma busca de força bruta. Em seguida, mostraremos como esse modelo salvo pode ser usado em um indicador, utilizando-o para fazer previsões com um passo à frente. Por fim, usaremos o mesmo modelo para criar um Expert Advisor simples.

//+------------------------------------------------------------------+
//|                                                 TrainARModel.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Arima.mqh>

enum ENUM_QUOTES
  {
   closeprices,//Close price
   medianprices//Mid price
  };

input uint MaximumSearchLag=5;
input bool DifferenceQuotes=true;
input datetime TrainingDataStartDate=D'2020.01.01 00:01';
input datetime TrainingDataStopDate=D'2021.01.01 23:59';
input string Sy="AUDUSD";//Set The Symbol
input ENUM_TIMEFRAMES SetTimeFrame=PERIOD_M1;
input ENUM_QUOTES quotestypes = closeprices;
input string SetModelName = "ModelName";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CArima *arima[];
   uint max_it=MaximumSearchLag;
   double sse[],quotes[],mid_prices[];


   if(!max_it)
      ++max_it;


   MqlRates prices[];

   int a_size=CopyRates(Sy,SetTimeFrame,TrainingDataStartDate,TrainingDataStopDate,prices);

   if(a_size<=0)
     {
      Print("downloaded size is ", a_size," error ",GetLastError());
      return;
     }

   ArrayResize(arima,max_it);
   ArrayResize(sse,max_it);
   ArrayResize(quotes,a_size);

   for(uint i=0; i<prices.Size(); i++)
     {

      switch(quotestypes)
        {
         case medianprices:
            quotes[i]=(prices[i].high+prices[i].low)/2;
            break;
         case closeprices:
            quotes[i]=prices[i].close;
            break;
        }
     }

   uint u=0;
   for(uint i=0; i<max_it; i++)
     {
      u=uint(DifferenceQuotes);
      arima[i]=new CArima(i+1,u,0,true);
      if(arima[i].Fit(quotes))
        {
         sse[i]=arima[i].GetSSE()*1.e14;
         Print("Fitting model ",i+1," completed successfully.");
        }
      else
        {
         sse[i]=DBL_MAX;
         Print("Fitting model ",i+1, " failed.");
        }


     }

   int index = ArrayMinimum(sse);
   Print("**** Saved model *****");
   arima[index].Summary();
//save the best model for later use.
   arima[index].SaveModel(SetModelName);

   for(int i=0; i<(int)arima.Size(); i++)
      if(CheckPointer(arima[i])==POINTER_DYNAMIC)
         delete arima[i];

  }
//+------------------------------------------------------------------+

O script facilita a localização do modelo autorregressivo puro ideal que se ajusta a uma amostra de preços de fechamento. Deve-se enfatizar que esta é apenas uma demonstração. Você pode implementar modelos mais complexos com variações no número e tipos de termos (AR/MA), ao mesmo tempo que pode especificar defasagens não adjacentes para esses termos. Portanto, as possibilidades são vastas. Por enquanto, nos limitaremos a selecionar um modelo autorregressivo puro.

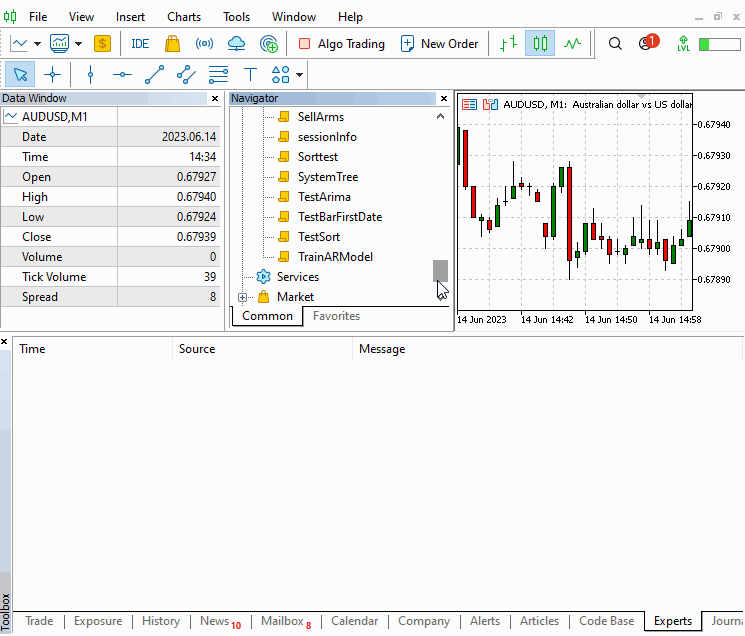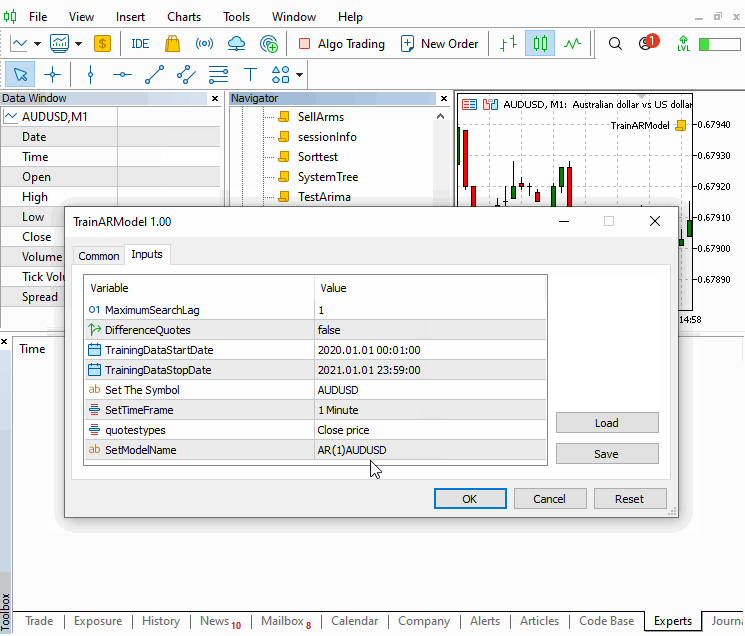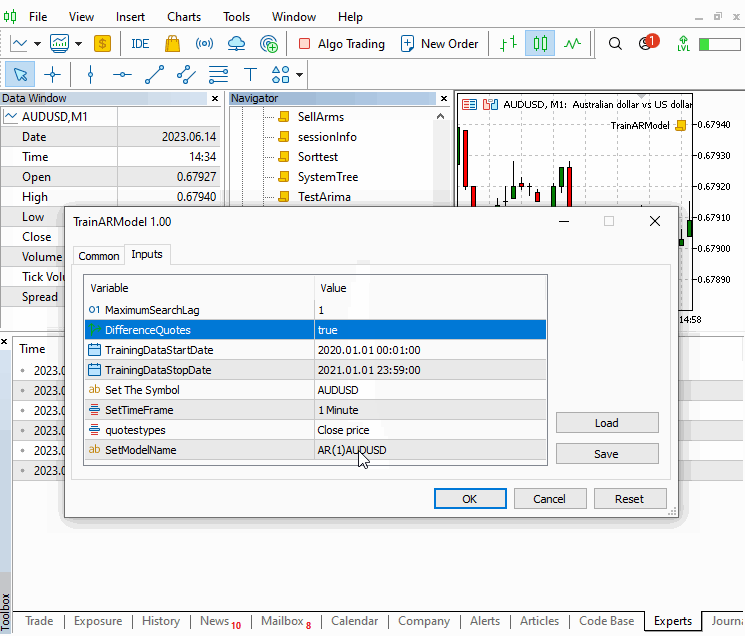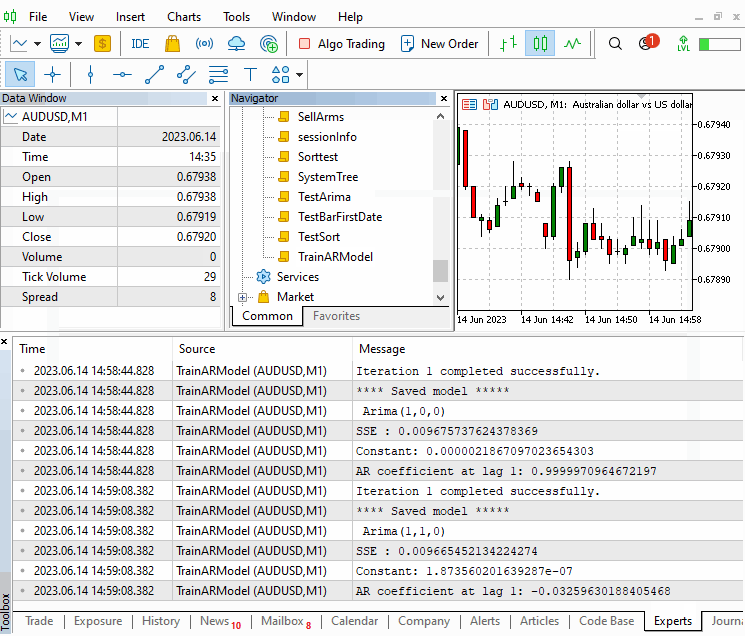
O script permite definir a ordem AR máxima para interromper a pesquisa, bem como o símbolo, prazo e período dos dados da amostra de preço. É importante usar preços de amostra que sejam representativos das condições que provavelmente serão encontradas ao aplicar o modelo para fazer previsões.

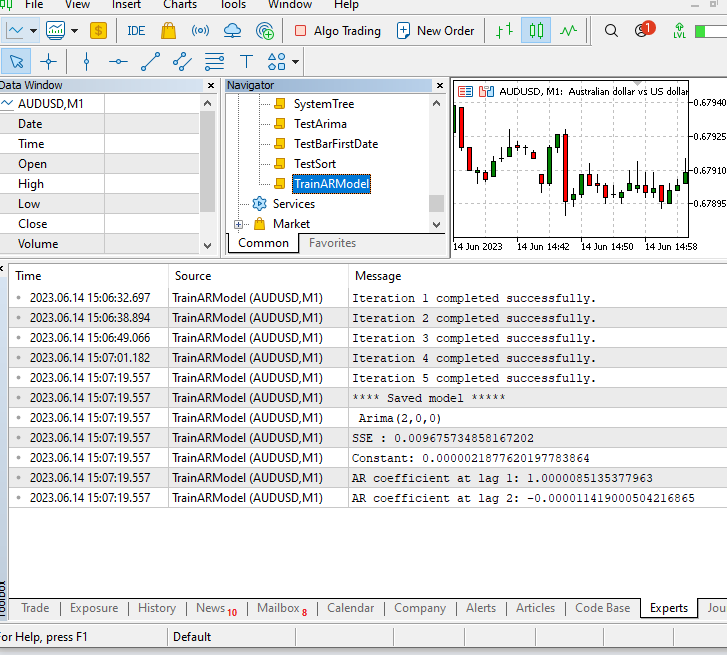
O script determina o modelo ideal selecionando aquele com o menor valor sse entre o conjunto de modelos treinados. O modelo selecionado é então salvo, e seus atributos são impressos no terminal.

//+------------------------------------------------------------------+
//|                                         ArimaOneStepForecast.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_plots   1
#include<Arima.mqh>
//--- plot PredictedPrice
#property indicator_label1  "PredictedPrice"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input string   ModelName = "Model name";

//--- indicator buffers
uint     NumberOfPredictions=1;
double         PredictedPriceBuffer[];
double         forecast[];
double         pricebuffer[];
uint         modelinputs;

CArima arima;
double mj[];

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,PredictedPriceBuffer,INDICATOR_DATA);


   ArraySetAsSeries(PredictedPriceBuffer,true);

   if(!arima.LoadModel(ModelName))
      return(INIT_FAILED);
//---
   modelinputs=arima.GetMinModelInputs();

   ArrayResize(pricebuffer,modelinputs);

   ArrayResize(forecast,NumberOfPredictions);

   if(modelinputs<=0)
      return(INIT_FAILED);

   arima.Summary();

   arima.GetModelParameters(mj);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   int limit = (prev_calculated<=0)?1000-(int)modelinputs-1:rates_total-prev_calculated+1;

   if(NewBar(time[0]))
     {
      for(int i = limit; i>=0; i--)
        {
         if(CopyClose(_Symbol,_Period,i+1,modelinputs,pricebuffer)==modelinputs)
            if(arima.Predict(NumberOfPredictions,pricebuffer,forecast))
               PredictedPriceBuffer[i]=forecast[NumberOfPredictions-1];
        }
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool NewBar(datetime c_time)
  {
   static datetime prev_time;

   if(c_time>prev_time)
     {
      prev_time=c_time;
      return true;
     }

   return false;
  }
//+------------------------------------------------------------------+

O indicador utiliza o modelo selecionado para fazer previsões com um passo à frente.

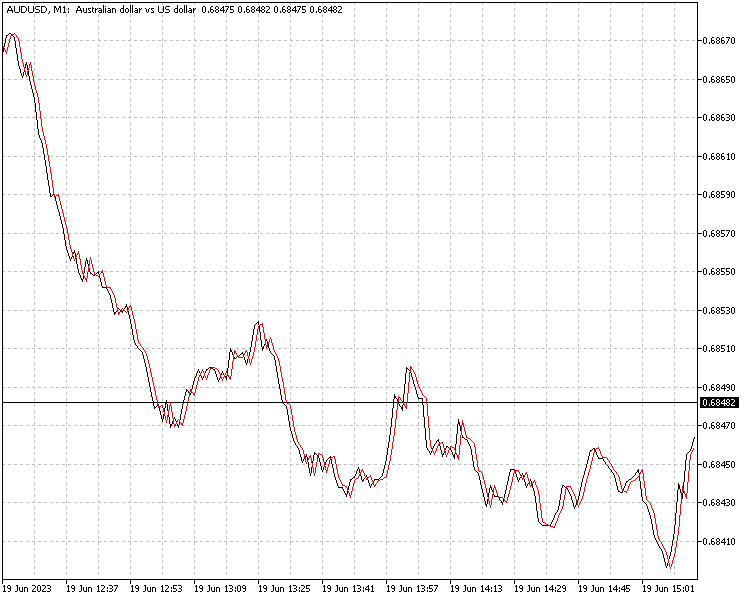
O modelo especificado é carregado durante a inicialização do indicador. O método Predict é então usado no loop principal do indicador para fazer previsões futuras com base nos preços de fechamento fornecidos.

//+------------------------------------------------------------------+
//|                                               ArForecasterEA.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include <Arima.mqh>
//---
input string ModelName   ="model name"; // Saved Arima model name
input long   InpMagicNumber = 87383;
input double InpLots          =0.1; // Lots
input int    InpTakeProfit    =40;  // Take Profit (in pips)
input int    InpTrailingStop  =30;  // Trailing Stop Level (in pips)

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int    InpOpenThreshold =1; // Differential to trigger trade (in points)
int    InpStopLoss     = 0;//   Stoploss (in pips)

//---
//+------------------------------------------------------------------+
//| ARIMA Sample expert class                                        |
//+------------------------------------------------------------------+
class CArExpert
  {
protected:
   double            m_adjusted_point;             // point value adjusted for 3 or 5 points
   CTrade            m_trade;                      // trading object
   CSymbolInfo       m_symbol;                     // symbol info object
   CPositionInfo     m_position;                   // trade position object
   CAccountInfo      m_account;                    // account info wrapper
   CArima            *m_arima;                      // Arma object pointer
   uint              m_inputs;                     // Minimum number of inputs for Arma model
   //--- indicator buffers
   double            m_buffer[];                   // close prices buffer
   double            m_pbuffer[1];                 // predicted close prices go here


   //---
   double            m_open_level;


   double            m_traling_stop;
   double            m_take_profit;
   double            m_stop_loss;

public:
                     CArExpert(void);
                    ~CArExpert(void);
   bool              Init(void);
   void              Deinit(void);
   void              OnTick(void);

protected:
   bool              InitCheckParameters(const int digits_adjust);
   bool              InitModel(void);
   bool              CheckForOpen(void);
   bool              LongModified(void);
   bool              ShortModified(void);
   bool              LongOpened(void);
   bool              ShortOpened(void);
  };

O Expert Advisor novamente aplica o modelo salvo para implementar uma estratégia simples. Com base na previsão do próximo fechamento, compramos se o fechamento previsto for maior do que o último fechamento conhecido. E vendemos se a previsão for menor. 

                                         

O código para a classe CArima completa e suas dependências estão contidos no arquivo ZIP anexado ao final do artigo, juntamente com o script, indicador e EA descritos no artigo.

Considerações finais

Os modelos de autorregressão são facilmente treinados com o terminal MetaTrader 5 e são usados em todos os tipos de programas. A parte mais difícil é a especificação e a seleção do modelo. Para superar esses desafios e criar modelos autorregressivos eficazes na análise do mercado Forex, os traders devem seguir algumas práticas recomendadas, que são:

• Comece com uma pergunta de pesquisa clara: antes de criar um modelo autorregressivo, os traders devem definir uma pergunta de pesquisa clara e a hipótese que desejam testar. Isso ajuda a garantir que o processo de modelagem permaneça focado e relevante para os objetivos do trader.

• Colete dados de alta qualidade: a precisão do modelo depende muito da qualidade dos dados usados. Os traders devem usar fontes de dados confiáveis e garantir que eles sejam limpos, completos e relevantes para a pergunta de pesquisa.

• Teste vários modelos: os traders devem testar vários modelos com diferentes latências e parâmetros para determinar o modelo mais preciso e eficiente para seus dados.

• Valide os modelos: depois de criar um modelo, os traders devem testar sua precisão usando métodos estatísticos.

• Monitore e ajuste o modelo: como as condições do mercado mudam com o tempo, a eficácia do modelo também pode mudar. Os traders devem monitorar o desempenho de seu modelo ao longo do tempo e fazer os ajustes necessários para que ele continue a prover uma representação precisa dos movimentos futuros de preços.

Seguindo essas práticas recomendadas, os traders podem criar modelos autorregressivos eficazes para analisar o mercado Forex e obter insights valiosos sobre as tendências futuras do mercado. Espero que o código seja útil para outros usuários e talvez os inspire a expandir ainda mais a biblioteca. Boa sorte!

Arquivo	Descrição
Mql5/include/Powells.mqh	arquivo include contendo a declaração e definição da classe CPowellsMethod
Mql5/include/Arima.mqh	arquivo include para a classe CArima
Mql5/indicator/ArimaOneStepForecast.mql5	código fonte do indicador mostrando como carregar e aplicar o modelo no indicador
Mql5/scripts/TrainARModel.mql5	script demonstrando como treinar um modelo e salvá-lo para uso posterior
Mql5/experts/ArForecasterEA.mql5	Expert Advisor mostrando o uso do modelo salvo no Expert Advisor.