Representações no domínio da frequência de séries temporais: O espectro de potência
Introdução
As cotações de preços que observamos nos gráficos representam dados distribuídos ao longo do tempo. A série de preços é dita estar no domínio do tempo. No entanto, esta não é a única maneira de expressar essa informação. Exibir os dados em diferentes domínios pode revelar características interessantes sobre a série que podem não ser aparentes ao realizar análises exclusivamente no domínio do tempo. Além disso, discutimos algumas perspectivas promissoras para a análise de séries temporais no domínio da frequência usando a transformada discreta de Fourier (DFT). Nos concentraremos na análise dos espectros de potência, fornecendo exemplos práticos de como calcular e reconhecer características de séries temporais identificadas usando esse método de análise. Também discutiremos brevemente técnicas importantes de pré-processamento que devem ser usadas antes de aplicar a transformada discreta de Fourier.
Transformada discreta de Fourier
Antes de demonstrarmos os métodos de análise do espectro de potência, primeiro temos que entender o que é o espectro de potência. A análise dos espectros de potência de séries temporais se enquadra no amplo tópico de processamento de sinais. No artigo "Indicadores técnicos e filtros digitais", o autor mostra como qualquer série complicada pode ser decomposta em formas comuns de ondas senoidais e cossenoidais. Isso torna possível reduzir um processo complexo em componentes simples. O que torna tudo isso possível é a representação no domínio da frequência escolhida. Isso se refere à base de representação, que é o conjunto de funções usadas para reproduzir uma série temporal.
Uma das representações mais comumente usadas de séries temporais no domínio da frequência é a transformada discreta de Fourier. Ela usa como base as ondas senoidais e cossenoidais que cobrem um ciclo ao longo de uma série. Sua característica mais valiosa é que qualquer série temporal descrita dessa forma é sempre definida de forma única, ou seja, não há duas séries que tenham representações idênticas no domínio da frequência. Um espectro de potência é uma representação de quanto poder, ou energia, um sinal possui em diferentes frequências. No contexto de dados de séries temporais, o espectro de potência fornece informações sobre a distribuição de energia nas diferentes frequências que compõem a série temporal.
Calculando a transformada discreta de Fourier
Para converter qualquer série no domínio da frequência usando a DPF, é usada a seguinte fórmula.
Onde cada termo é um número complexo e x é a série de dados bruta. Cada termo representa um componente periódico que se repete exatamente j vezes ao longo de todo o intervalo de valores. A transformada rápida de Fourier é um algoritmo que acelera o cálculo das transformadas discretas de Fourier. Ela divide recursivamente uma série ao meio, transforma cada metade e, eventualmente, combina os resultados.
O espectro de potência
Aplicando alguma matemática básica, podemos calcular a quantidade de energia devido a um componente de frequência. Traçando um número complexo em um plano cartesiano, onde a parte real é plotada no eixo x e a parte imaginária no eixo y, podemos aplicar o teorema de Pitágoras, que estabelece que o valor absoluto é a raiz quadrada da soma dos quadrados de ambas as partes reais e imaginárias. Portanto, a energia devida a uma determinada frequência é o quadrado de seu valor absoluto. A potência é calculada dividindo o quadrado do valor absoluto pela raiz quadrada do número de valores na série no domínio do tempo.
Mas antes de aplicarmos o cálculo bruto da DFT a uma série, precisamos passar por algumas etapas de pré-processamento para obter uma estimativa precisa da potência em uma frequência específica. Isso é necessário porque a DFT opera em segmentos de dados de comprimento finito e assume que o sinal de entrada é periódico, o que pode levar a vazamentos espectrais e outras distorções se os valores não atenderem a essa suposição. Para atenuar esses problemas, é aplicado o janelamento.
Função de janela
O janelamento se refere ao processo de multiplicar uma série temporal por uma função de janela, que é uma função matemática que atribui pesos a diferentes pontos na série temporal. O janelamento é uma etapa importante na preparação de dados de séries temporais para análise usando a transformada discreta de Fourier.
Quando analisamos dados de séries temporais usando a DFT, dividimos os dados em segmentos menores. Se não adicionarmos uma moldura (neste caso, uma função de janela) em torno de cada segmento, podemos perder algumas informações importantes e nossa análise será incompleta. O janelamento estreita as extremidades da série temporal, reduzindo as transições abruptas nas fronteiras da janela da DFT. A função de estreitamento geralmente é projetada para reduzir suavemente o sinal a zero nas bordas da janela, o que reduz a amplitude de qualquer componente espectral próximo à borda da janela.
No entanto, este processo introduz alguns problemas que podem causar distorção ou alterações na forma bruta dos dados. A maioria desses problemas pode ser eliminada ou minimizada centralizando a série antes de aplicar uma função de janela à série bruta. Quando uma série temporal é centralizada, o valor médio é subtraído de cada ponto de dados na série, resultando em uma nova série com média zero.
Existem muitas funções de janela disponíveis, como a janela retangular, a janela de Hamming, a janela de Hanning, a janela de Blackman e a janela de Kaiser, cada uma com suas próprias propriedades e casos de uso exclusivos. Neste texto, usaremos o janelamento Welch (Welch data window), que é outro método popular.
Esse janelamento é dado pela fórmula abaixo.
Cada valor da série temporal original deve ser multiplicado pelo correspondente m(i).
Para centralizar os valores, a média ponderada da série é calculada usando a função de janela. Essa média é então subtraída de cada ponto na série antes da aplicação da janela em si.
Suavizando o espectro de potência
O espectro de potência discreto pode ser difícil de interpretar, pois geralmente há muitos picos estreitos, sobressaindo em todos os lugares. Para ter uma melhor compreensão do que está acontecendo, pode ser necessário empregar alguma suavização. O filtro de Saviztky Golay geralmente é a escolha preferida nessas aplicações. Sua função de filtragem é definida por dois parâmetros, o comprimento pela metade e o grau dos polinômios. O comprimento pela metade especifica o número de valores adjacentes (antes e depois) a um valor que está sendo filtrado. Os graus definem o grau do polinômio a ser ajustado ao valor atual e aos valores adjacentes.
A classe CSpectrum
Nesta seção, apresentamos uma classe que permite a análise fácil de séries em MQL5. Um dos destaques da classe inclui a implementação de um método de plotagem que facilita a exibição de vários gráficos espectrais usando algumas linhas de código.
A classe inteira é definida abaixo.
//+------------------------------------------------------------------+ //| Spectrum.mqh | //| Copyright 2023, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Software Corp." #property link "https://www.mql5.com" #include<Math\Stat\Math.mqh> #include<Math\Alglib\fasttransforms.mqh> #include<Graphics\Graphic.mqh> enum ENUM_SPECTRUM_PLOT { PLOT_POWER_SPECTRUM=0,//PowerSpectrum PLOT_FILTERED_POWER_SPECTRUM,//FilteredPowerSpectrum PLOT_CUMULATIVE_SPECTRUM_DEVIATION//CumulativeSpectrumDeviation }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSpectrumAnalysis { private: bool m_window,m_initialized; int m_n,m_cases; complex m_dft[]; double m_real[]; double m_win,m_win2; double m_wsq; double m_wsum,m_dsum; int m_window_size,m_poly_order; void savgol(double &data[], double&out[], int window_size, int poly_order); public: //---constructor CSpectrumAnalysis(const bool window,double &in_series[]); //---destructor ~CSpectrumAnalysis(void) { if(m_n) { ArrayFree(m_dft); ArrayFree(m_real); } } bool PowerSpectrum(double &out_p[]); bool CumulativePowerSpectrum(double & out_cp[]); double CumulativeSpectrumDeviation(double &out_csd[]); void Plot(ENUM_SPECTRUM_PLOT plot_series,int window_size=5, int poly_order=2, color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400); };
Para usá-la, o usuário chama o construtor paramétrico passando dois parâmetros. O primeiro parâmetro especifica se aplicar uma função de janela aos dados. É importante observar que, ao usar a função de janela, a linha também é centralizada. O segundo parâmetro para o construtor é um array que contém os valores brutos a serem analisados.
A transformação de Fourier é feita no construtor e os valores complexos associados ao espectro são armazenados no array DFT.
void CSpectrumAnalysis::CSpectrumAnalysis(const bool apply_window,double &in_series[]) { int n=ArraySize(in_series); m_initialized=false; if(n<=0) return; m_cases=(n/2)+1; m_n=n; m_window=apply_window; ArrayResize(m_real,n); if(m_window) { m_wsum=m_dsum=m_wsq=0; for(int i=0; i<n; i++) { m_win=(i-0.5*(n-1))/(0.5*(n+1)); m_win=1.0-m_win*m_win; m_wsum+=m_win; m_dsum+=m_win*in_series[i]; m_wsq+=m_win*m_win; } m_dsum/=m_wsum; m_wsq=1.0/sqrt(n*m_wsq); } else { m_dsum=0; m_wsq=1.0; } for(int i=0; i<n; i++) { if(m_window) { m_win=(i-0.5*(n-1))/(0.5*(n+1)); m_win=1.0-m_win*m_win; } else m_win=1.0; m_win*=m_wsq; m_real[i]=m_win*(in_series[i]-m_dsum); } CFastFourierTransform::FFTR1D(m_real,n,m_dft); m_initialized=true; }
Para calcular e obter os valores do espectro de potência, espectro de potência cumulativo e também o desvio cumulativo do espectro, a classe fornece os métodos PowerSpectrum(), CumulativePowerSpectrum() e CumulativeSpectrumDeviation(), respectivamente. Cada método requer um único parâmetro de array, onde os valores correspondentes serão copiados.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CSpectrumAnalysis::PowerSpectrum(double &out_p[]) { if(!m_initialized) return false; ArrayResize(out_p,m_cases); for(int i=0; i<m_cases; i++) { out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im; if(i && (i<(m_cases-1))) out_p[i]*=2; } return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CSpectrumAnalysis::CumulativePowerSpectrum(double &out_cp[]) { if(!m_initialized) return false; double out_p[]; ArrayResize(out_p,m_cases); ArrayResize(out_cp,m_cases); for(int i=0; i<m_cases; i++) { out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im; if(i && (i<(m_cases-1))) out_p[i]*=2; } for(int i=0; i<m_cases; i++) { out_cp[i]=0; for(int j=i; j>=1; j--) out_cp[i]+=out_p[j]; } ArrayFree(out_p); return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSpectrumAnalysis::CumulativeSpectrumDeviation(double &out_csd[]) { if(!m_initialized) return 0; ArrayResize(out_csd,m_cases); double sum=0; for(int i=0; i<m_cases; i++) { out_csd[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im; if(i==(m_cases-1)) out_csd[i]*=0.5; sum+=out_csd[i]; } double sfac=1.0/sum; double nfac=1.0/(m_cases-1); double dmax=sum=0; for(int i=1; i<m_cases-1; i++) { sum+=out_csd[i]; out_csd[i]=sum*sfac - i*nfac; if(MathAbs(out_csd[i])>dmax) dmax=MathAbs(out_csd[i]); } out_csd[0]=out_csd[m_cases-1]=0; return dmax; }
O último método a ser analisado é a função Plot(). Com ele, o usuário pode rapidamente exibir um gráfico dentre três opções definidas pela enumeração ENUM_SPECTRUM_PLOT. O segundo e terceiro parâmetros do método Plot() definem os parâmetros de suavização aplicados ao filtro de Savitzky-Golay ao plotar o espectro de potência cumulativo filtrado. Quando outros gráficos são selecionados, esses parâmetros não têm efeito. Os demais parâmetros de Plot() controlam a cor do gráfico de linha, o tempo de exibição gráfica em segundos e o tamanho do gráfico, respectivamente.
void CSpectrumAnalysis::Plot(ENUM_SPECTRUM_PLOT plot_series,int windowsize=5, int polyorder=2,color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400) { double x[],y[]; bool calculated=false; string header=""; switch(plot_series) { case PLOT_POWER_SPECTRUM: ArrayResize(x,m_cases); calculated=PowerSpectrum(y); for(int i=0; i<m_cases; i++) x[i]=double(i)/double(m_n); header="Power Spectrum"; break; case PLOT_FILTERED_POWER_SPECTRUM: { double ps[] ; calculated=PowerSpectrum(ps); savgol(ps,y,windowsize,polyorder); ArrayResize(x,ArraySize(y)); for(int i=0; i<ArraySize(y); i++) x[i]=double((i+(windowsize/2))/double(m_n)); header="Filtered Power Spectrum"; } break; case PLOT_CUMULATIVE_SPECTRUM_DEVIATION: calculated=CumulativeSpectrumDeviation(y); ArrayResize(x,m_cases); for(int i=0; i<m_cases; i++) x[i]=i; header="Cumulative Spectrum Deviation"; break; } if(!calculated) { ArrayFree(x); ArrayFree(y); return; } ChartSetInteger(0,CHART_SHOW,false); long chart=0; string name=EnumToString(plot_series); CGraphic graphic; if(ObjectFind(chart,name)<0) graphic.Create(chart,name,0,0,0,size_x,size_y); else graphic.Attach(chart,name); //--- graphic.BackgroundMain(header); graphic.BackgroundMainSize(16); graphic.CurveAdd(x,y,ColorToARGB(line_color),CURVE_LINES); //--- graphic.CurvePlotAll(); //--- graphic.Update(); //--- Sleep(display_time_seconds*1000); //--- ChartSetInteger(0,CHART_SHOW,true); //--- graphic.Destroy(); //--- ChartRedraw(); //--- }
Para facilitar o entendimento, analisaremos as características espectrais de algumas séries hipotéticas com características particulares, ou seja, uma série autorregressiva com um único termo positivo ou negativo, uma série com componentes sazonais e de tendência óbvias. Finalmente, daremos uma olhada na natureza espectral de um processo aleatório.
Identificando padrões sazonais em séries temporais
Normalmente, ao construir modelos de previsão, precisamos aplicar algumas etapas de pré-processamento antes de avançar. É prática comum remover quaisquer características óbvias, como tendência ou sazonalidade, antes de usar uma rede neural para prever a série. Uma maneira de detectar tais características é avaliar o espectro de potência. Componentes fortes que determinam a série geralmente se revelarão como picos amplos. Vamos considerar um exemplo, considerando uma série determinística que possui um componente sazonal óbvio. A série é gerada pelo código mostrado abaixo.
input bool Add_trend=false; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- int num_samples = 100; double inputs[]; ArrayResize(inputs,num_samples); MathSrand(2023); //--- for(int i=0;i<num_samples;i++) { inputs[i]=(Add_trend)?i*0.03*-1:0; inputs[i]+= cos(2*M_PI*0.1*(i+1)) + sin(2*M_PI*0.4*(i+1)) + (double)rand()/SHORT_MAX; } //---
A visualização desses valores é mostrada nos gráficos a seguir, o primeiro representando os valores com a tendência adicionada e o último mostrando o gráfico sem o componente de tendência.
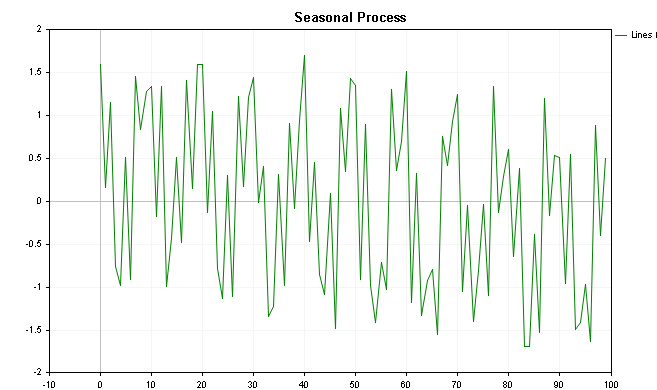
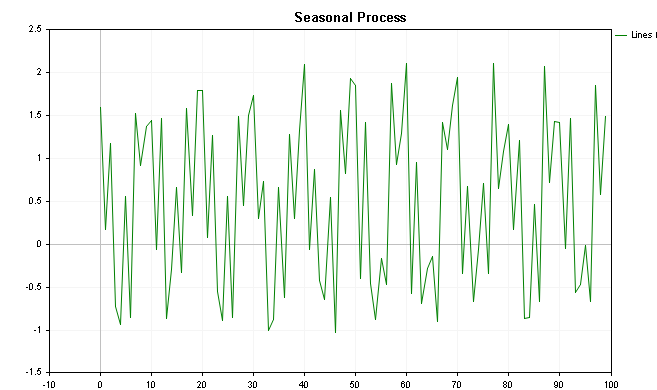
Ao colocar a classe CSpectrum para trabalhar, podemos visualizar o espectro de potência desta série, como mostrado abaixo. Podemos ver que o espectro de potência claramente mostra alguns picos proeminentes.
CSpectrumAnalysis sp(true,inputs);
sp.Plot(PLOT_POWER_SPECTRUM); 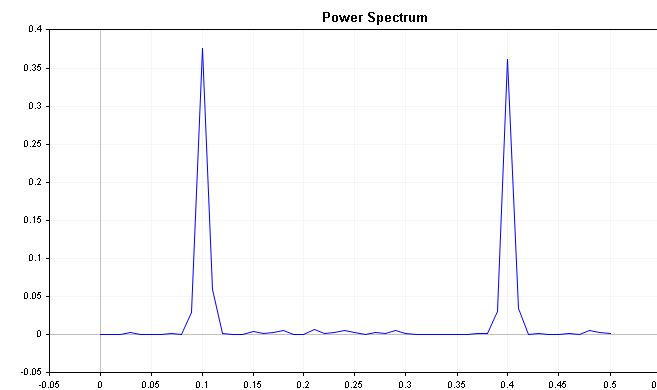
O gráfico mostra claramente que a série é fortemente influenciada pelos componentes de frequência em 0,2 e 0,4, respectivamente.
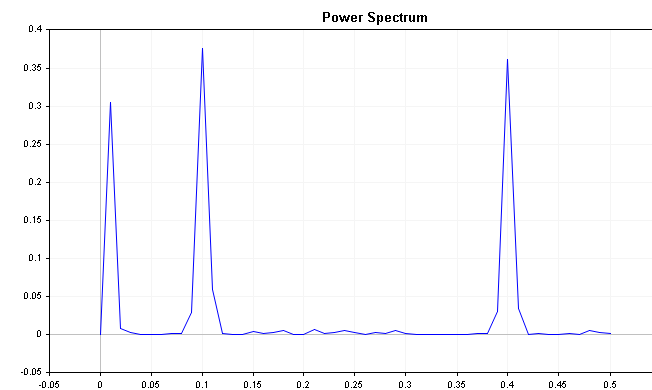
O espectro da série com uma leve tendência descendente mostra um pico inicial junto com o componente sazonal. Em uma situação como essa, pode ser prudente não apenas diferenciar a série, mas também aplicar uma diferenciação sazonal. É importante notar que a existência de tais picos nem sempre indica uma tendência e/ou sazonalidade. O exemplo mostrado tem um componente de ruído bastante moderado, enquanto conjuntos de dados do mundo real, como séries financeiras, são frequentemente afetados por ruídos. A sazonalidade em uma série geralmente se manifesta como um pico evidente no gráfico do espectro de potência.
Determinando a ordem de um modelo autorregressivo (AR)
Os modelos autorregressivos são comumente usados na análise de séries temporais para prever valores futuros de uma série com base em seus valores passados. A ordem do modelo AR determina quantos valores passados são usados para prever o próximo valor. Um método para determinar a ordem apropriada para um modelo AR é examinar o espectro de potência da série temporal.
Normalmente, o espectro de potência diminuirá à medida que a frequência aumenta. Por exemplo, uma série temporal definida por um termo autorregressivo positivo de curto prazo terá a maior parte de sua energia espectral concentrada em baixas frequências, enquanto uma série com um termo autorregressivo negativo de curto prazo deslocará sua energia espectral para altas frequências.
Vamos ver como isso se parece na prática usando outra série determinística definida por um componente autorregressivo positivo ou negativo. O código para gerar a série é mostrado abaixo.
double inputs[300]; ArrayInitialize(inputs,0); MathSrand(2023); for(int i=1; i<ArraySize(inputs); i++) { inputs[i]= 0.0; switch(Coeff_Mult) { case positive: inputs[i]+= 0.9*inputs[i-1]; break; case negative: inputs[i]+= -1*0.9*inputs[i-1]; break; } inputs[i]+=(double)rand() / double(SHORT_MAX); }
Quando a série é definida por autorregressão positiva, o espectro de potência mostra que a maior parte da energia está concentrada nas baixas frequências, com a potência diminuindo nas frequências mais altas ao longo da extensão dos valores.
Compare isso com o gráfico da série autorregressiva com um termo negativo e você verá que a potência aumenta ao amostrar frequências mais altas. Novamente, este é um exemplo simples, mas ele demonstra características importantes que podem ser aplicadas na construção de modelos autorregressivos.
Estudo do espectro de distribuição de erros para avaliar o desempenho do modelo de previsão
Finalmente, podemos usar o espectro de potência da distribuição de erros de um modelo de previsão para avaliar o quão bem ele modela um processo. Para fazer isso, primeiro ajustamos um modelo de previsão aos dados da série temporal e calculamos os resíduos ou erros (a diferença entre os valores previstos e reais).
Em seguida, examinamos o espectro de potência da distribuição de erros. Um bom modelo de previsão terá resíduos que se comportam como ruído branco, o que significa que o espectro de potência da distribuição de erros deve ser relativamente uniforme em todas as frequências. Picos proeminentes no espectro de potência em qualquer frequência sugerem que o modelo de previsão não está capturando todas as informações nos dados da série temporal, e pode ser necessário um ajuste adicional. O problema é que, na realidade, o espectro de potência do ruído branco geralmente não é uniforme como se espera. Basta olhar o espectro de uma série de ruído branco gerada a partir do código abaixo.
int num_samples = 500; double inputs[]; MathSrand(2023); ArrayResize(inputs,num_samples); for (int i = 0; i < num_samples; i++) { inputs[i] = ((double)rand() / SHORT_MAX) * 32767 - 32767/2; }
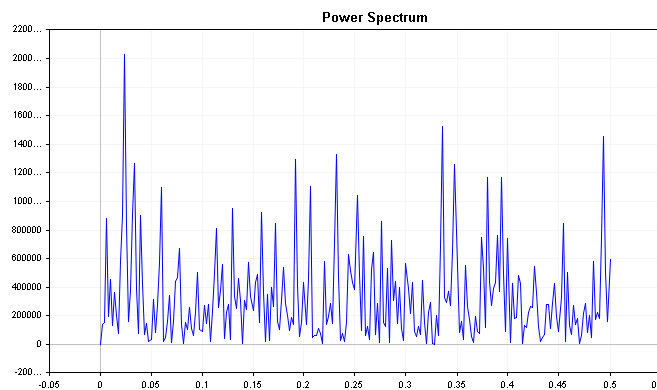
Para obter uma imagem mais clara dos componentes de frequência, podemos usar o espectro de potência cumulativo.
Teoricamente, se uma série temporal for ruído branco, todos os termos espectrais seriam iguais, portanto, o gráfico do espectro de potência cumulativo deve ser reto. Em particular, a fração da potência total contabilizada até cada termo individual deve ser igual à fração do número total de termos acumulados. Matematicamente, isso significa que a potência cumulativa do ruído branco tem uma expectativa determinística. A equação que define a potência cumulativa para cada banda de frequência amostrada é mostrada abaixo.
Se o espectro de potência mostrar uma alta concentração de energia em frequências baixas ou altas, veremos desvios em relação à forma teórica do ruído branco. Usando esse fato, podemos calcular o desvio entre os espectros cumulativos observados e teóricos, obtendo o desvio cumulativo do espectro.
Esta série pode revelar informações importantes sobre a série temporal. Por exemplo, se a energia espectral for deslocada para a esquerda, o desvio começará próximo de zero e aumentará lentamente até convergir muito mais tarde. Por outro lado, se a energia espectral for deslocada para a direita, o desvio imediatamente cairá para valores negativos e depois aumentará lentamente até voltar a zero ao longo do tempo. O ruído branco produzirá valores de desvio que variam muito menos em relação a zero.
Os gráficos abaixo mostram o desvio cumulativo do espectro de processos AR(1) positivos e negativos definidos anteriormente. Compare-os com o gráfico cumulativo do espectro de ruído branco e observe as distinções mais claras.
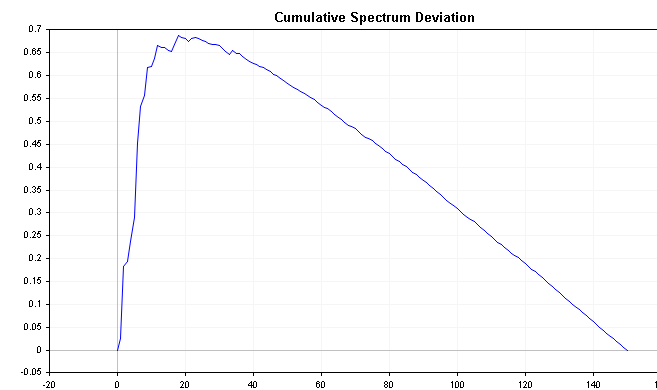
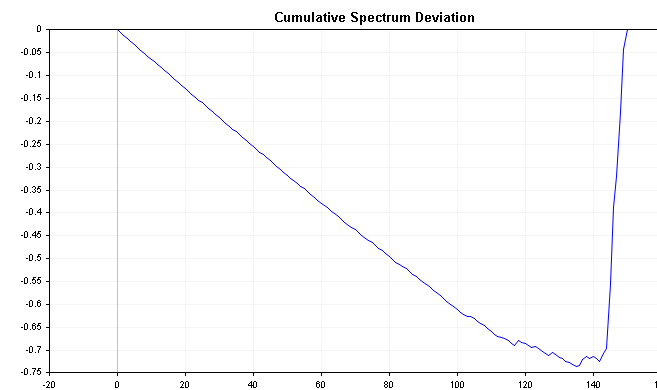
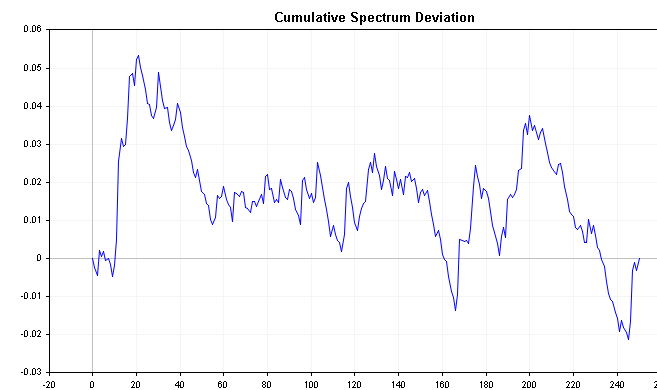
Sabe-se que a distribuição do valor absoluto máximo de todos os desvios segue a distribuição de Komogorov-Smirnov. Aplicando a fórmula abaixo, podemos testar diretamente a hipótese de que a série temporal é ruído branco. Esta fórmula calcula a estatística D de uma série.
q define os graus de liberdade, se a DFT for aplicada a uma série temporal real, q = n/2-1. Se um janelamento Welch for aplicado antes da DFT, q deve ser multiplicado por 0,72 para compensar a perda de informações causada pela janela. Alpha é o nível de significância geralmente em porcentagem. Para testar a hipótese de ruído branco, obtenha a diferença máxima ou desvio e compare-a com a estatística D.
Na classe CSpectrum, podemos obter a diferença máxima determinada pelos cálculos do desvio cumulativo do espectro chamando o método CumulativeSpectrumDeviation().
Considerações finais
O foco deste artigo foi na DFT para estimar o espectro de potência de uma série temporal, como é bem conhecido. No entanto, existe um método alternativo chamado método de máxima entropia (ME) que às vezes pode superar a DFT. O espectro ME tem a capacidade de ampliar características muito estreitas enquanto suaviza áreas com baixa energia espectral, resultando em uma exibição abrangente. No entanto, o método ME tende a encontrar picos de alta energia espectral mesmo quando eles não existem, tornando-o inadequado para ser usado sozinho. Portanto, o espectro da DFT deve sempre ser analisado ao lado dele, servindo como uma segunda opinião, por assim dizer.
Em conclusão, analisar o espectro de potência de dados de séries temporais pode fornecer informações valiosas sobre vários aspectos da análise de séries temporais, como determinar a ordem de um modelo AR, saber a necessidade de diferenciação sazonal como etapa de pré-processamento e examinar o desempenho de modelos de previsão.
| Nome do arquivo | Descrição |
|---|---|
| mql5files\include\Spectrum.mqh | Definição da classe CSpectrum |
| mql5files\scripts\OrderOneARProcess.mql5 | O script gera uma série temporal autorregressiva e aplica a classe CSpectrum |
| mql5files\scripts\SeasonalProcess.mql5 | O script gera uma série temporal com sazonalidade e aplica a classe CSpectrum |
| mql5files\scripts\WhiteNoise.mql5 | O script gera uma série temporal de ruído branco e aplica a classe CSpectrum |
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/12701
- Aplicativos de negociação gratuitos
- VPS Forex grátis por 24 horas
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso