Forex ticaretinin arkasındaki temel matematik

Giriş

5 yılı aşkın deneyime sahip bir otomatik strateji ve yazılım geliştiricisiyim. Bu makalede, Forex’te veya diğer finansal enstrümanlarda ticaret yapmaya yeni başlayanlar için gizem perdesini aralayacağız. Ayrıca, en popüler ticaret sorularını yanıtlamaya çalışacağız.

Umarım makale hem yeni başlayanlar hem de deneyimli yatırımcılar için faydalı olur. Ek olarak, burada anlatacaklarımın nihai bir hakikat olmadığını, tamamen benim deneyim ve araştırmalarıma dayanan görüşlerim olduğunu hatırlatmak isterim.

Ele alacağımız robotlardan ve göstergelerden bazıları ürünlerimde yer almaktadır. Ancak bu sadece küçük bir kısmıdır. Çok çeşitli stratejiler için çok çeşitli robotlar geliştirdim. Makale süresince, sunacağımız yaklaşımın piyasanın gerçek doğası hakkında fikir edinmeyi nasıl sağladığını ve hangi stratejilerin dikkate alınmaya değer olduğunu göstermeye çalışacağım.

Giriş ve çıkış noktalarını bulmak neden bu kadar zor?

Piyasaya nereden girip çıkacağınızı biliyorsanız, muhtemelen başka bir şey bilmenize gerek yoktur. Ne yazık ki, giriş/çıkış noktaları konusu anlaşılması zor bir konudur. İlk bakışta her zaman bir model belirleyebilir ve onu bir süre takip edebiliriz. Ancak sofistike araçlar ve göstergeler olmadan pek çok modeli nasıl tespit edebiliriz? En basit ve her zaman karşımıza çıkan modeller TREND ve YATAY'dır. Trend tek yönde uzun vadeli bir hareket iken, Yatay sık terse dönüşlerdir.

Bu modeller, insan gözü herhangi bir gösterge olmaksızın onları bulabildiği için kolayca tespit edilebilir. Buradaki temel sorun, bir modeli ancak tetiklendikten sonra görebilmemizdir. Dahası, hiç kimse herhangi bir modelin var olduğunu garanti edemez. Strateji ne olursa olsun hiçbir model bakiyenizi yok olmaktan kurtaramaz. Matematik dilini kullanarak bunun olası nedenlerini ortaya koymaya çalışacağım.

Piyasa mekanizmaları ve seviyeleri

Burada size fiyatlama ve piyasa fiyatını hareket ettiren güçler hakkında biraz bilgi vereceğim. Piyasada iki güç vardır - Piyasa ve Limit. Benzer şekilde de iki tür emir vardır - piyasa ve limit emirleri. Limit alıcıları ve satıcıları piyasa derinliğini doldururken, piyasadakiler onu parçalar. Piyasa derinliği temel olarak bir şeyi almak veya satmak isteyenleri gösteren dikey bir fiyat ölçeğidir. Limit satıcıları ile alıcıları arasında her zaman bir boşluk vardır. Bu boşluğa makas adı verilir. Makas, en iyi alış ve satış fiyatı arasındaki minimum fiyat hareketinin miktarını yansıtan mesafedir. Alıcılar en ucuz fiyattan satın almak isterken, satıcılar en yüksek fiyattan satmak isterler. Dolayısıyla, alıcıların limit emirleri her zaman altta yer alırken, satıcıların emirleri her zaman üstte yer alır. Piyasa alıcıları ve satıcıları piyasa derinliğine girer ve iki emir (limit ve piyasa emirleri) birbirine bağlanır. Piyasa hareketi, bir limit emri tetiklendiğinde gerçekleşir.

Aktif bir piyasa emri, genellikle Zararı Durdur ve Kârı Al emirlerine sahiptir. Limit emirlerine benzer şekilde, bu durma seviyeleri piyasanın her yerine dağılmış olup fiyatı hızlandırıcı veya terse döndürücü seviyeleri oluşturur. Her şey durma seviyelerinin miktarına ve türüne ve ayrıca işlem hacmine bağlıdır. Bu seviyeleri bilerek, fiyatın nerede hızlanabileceğini veya terse dönebileceğini söyleyebiliriz.

Limit emirleri, içerisinden geçilmesi zor dalgalanmalar ve kümeler oluşturabilir. Genellikle günün veya haftanın açılışı gibi önemli fiyat noktalarında ortaya çıkarlar. Seviye bazlı ticaretten bahsederken, yatırımcılar genellikle limit emir seviyelerini kullanmayı kasteder. Tüm bunlar kısaca aşağıdaki gibi gösterilebilir:

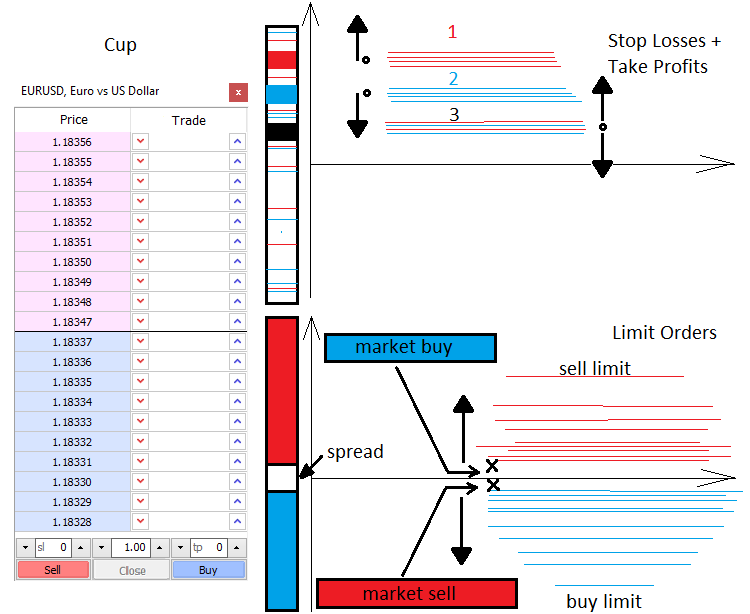
Piyasanın matematiksel tanımı

MetaTrader penceresinde gördüğümüz şey, t argümanının ayrık bir fonksiyonudur, burada t zamandır. Fonksiyon ayrıktır çünkü tik sayısı sonludur. Mevcut durumda tikler, aralarında hiçbir şey içermeyen noktalardır. Tikler, olası fiyat ayrıklaştırmasının en küçük öğeleridir, daha büyük öğeler çubuklar, M1, M5, M15 mumları ve benzeridir. Piyasada hem rastgele unsurlar hem de modeller bulunmaktadır. Modeller çeşitli ölçeklerde ve sürelerde olabilir. Bununla birlikte, piyasa çoğunlukla olasılıklı, kaotik ve neredeyse öngörülemez bir ortamdır. Piyasayı anlamak için, onu olasılık teorisinin kavramları aracılığıyla incelemek gerekir. Olasılık ve olasılık yoğunluğu kavramlarını tanıtmak için ayrıklaştırma gereklidir. 

Beklenen getiri kavramını tanıtmak için öncelikle 'olay' ve 'kapsamlı olaylar' terimlerini ele almamız gerekir:

• C1 olayı - Kâr, tp'ye eşittir
• C2 olayı - Zarar, sl'ye eşittir
• P1 - C1 olayının olasılığı
• P2 - C2 olayının olasılığı

С1 ve С2 olayları bir antitetik kapsamlı olaylar grubu oluşturur (yani her durumda bu olaylardan biri gerçekleşir). Dolayısıyla, bu olasılıkların toplamı bire eşittir: P1(tp,sl)+P2(tp,sl) = 1. Bu denklem daha sonra işe yarayabilir.

Bir Uzman Danışman veya manuel stratejiyi rastgele bir açılışla ve rastgele Zararı Durdur ve Kârı Al ile test ederken, yine de rastgele olmayan bir sonuç, "-(makas)" değerine eşit beklenen getiri elde ederiz, bu da makası sıfıra ayarlayabilseydik "0" anlamına gelirdi. Bu, durma seviyelerinden bağımsız olarak rastgele piyasada her zaman sıfır beklenen getiri elde edeceğimizi göstermektedir. Rastgele olmayan piyasada ise piyasanın ilgili modellere sahip olması koşuluyla her zaman bir kâr veya zarar elde ederiz. Beklenen getirinin (Tick[0].Bid-Tick[1].Bid) de sıfıra eşit olduğunu varsayarak aynı çıkarıma ulaşabiliriz. Bunlar, birçok şekilde ulaşılabilecek oldukça basit çıkarımlardır.

• M = P1*tp-P2*sl = P1*tp-(1- P1)*sl - herhangi bir piyasa için
  
  
• P1*tp-P2*sl = 0 - kaotik piyasa için
  

Bu, kaotik piyasanın temel formülüdür ve durma seviyelerine sahip emirlerin kaotik bir şekilde açılması ve kapanmasının beklenen getirisini tanımlar. Son denklemi çözdüğümüzde, durma değerlerini bilmemiz koşuluyla, hem tam rastgelelik hem de tersi durum için ilgilendiğimiz tüm olasılıkları elde ederiz. 

Burada sunulan denklem, herhangi bir strateji için genelleştirilebilecek en basit durum içindir. Sıfırdan farklı hale getirmemiz gereken nihai beklenen getirinin nelerden oluştuğunu tam olarak anlayabilmek adına şimdi yapacağımız şey de budur. Ayrıca, kâr faktörü kavramını tanıtacağız ve ilgili denklemleri yazacağız.

Stratejimizin hem durma seviyeleri hem de diğer bazı sinyallerle kapanmayı içerdiğini varsayalım. Bu amaçla, ilk olayın durma seviyeleri tarafından kapatıldığı, ikincisinin ise sinyaller tarafından kapatıldığı С3, С4 olay uzayını tanıtacağız. Bunlar aynı zamanda bir antitetik kapsamlı olaylar grubu oluştururlar, dolayısıyla analoji yoluyla şunu yazabiliriz:

M = P3*M3+P4*M4 = P3*M3+(1-P3)*M4, burada M3 = P1*tp-(1- P1)*sl,  M4 = Sum(P0[i]*pr[i])-Sum(P01[j]*ls[j]); Sum(P0[i])+Sum(P01[j]) = 1

• M3 - bir durma emri ile kapanırken beklenen getiri
• M4 - bir sinyal ile kapanırken beklenen getiri
• P1, P2 - her durumda durma seviyelerinden birinin tetiklenmesi koşuluyla, durma seviyelerinin etkinleşme olasılıkları
  
• P0[i] - durma seviyelerinin tetiklenmemiş olması koşuluyla, bir işlemin pr[i] kârı ile kapanma olasılığı. i - kapanış seçeneğinin numarası
  
• P01[j] - durma seviyelerinin tetiklenmemiş olması koşuluyla, bir işlemin ls[j] zararı ile kapanma olasılığı. j - kapanış seçeneğinin numarası
  

Başka bir deyişle, elimizde antitetik iki olay vardır. Onların sonuçları, kapsamlı olaylar grubunu da tanımladığımız iki bağımsız olay uzayı daha oluşturur. Ancak, P1, P2, P0[i] ve P01[j] olasılıkları artık koşulludur, P3 ve P4 ise hipotezlerin olasılıklarıdır. Koşullu olasılık, bir hipotez gerçekleştiğinde bir olayın gerçekleşme olasılığıdır. Her şey toplam olasılık formülüne (Bayes formülü) tam olarak uygundur. Konuyu kavramak için iyice incelemenizi şiddetle tavsiye ederim. Tamamen kaotik bir ticaret için M=0'dır.

Şimdi denklem, hem durma seviyeleri hem de sinyallerle kapanmayı dikkate aldığı için çok daha net ve geniş hale geldi. Bu analojiyi daha da ileri götürebilir ve dinamik durma seviyelerini bile hesaba katan herhangi bir strateji için genel denklemi yazabiliriz. Şimdi bunu yapacağız. Aynı Zararı Durdur ve Kârı Al ile açılan işlemler anlamına gelen bir kapsamlı olaylar grubu oluşturan N yeni olayı tanıtalım. CS[1] .. CS[2] .. CS[3] ....... CS[N]. Benzer şekilde, PS[1]+PS[2]+PS[3]+.......+PS[N] = 1.

M = PS[1]*MS[1]+PS[2]*MS[2]+...+PS[k]*MS[k]+...+PS[N]*MS[N], MS[k] = P3[k]*M3[k]+(1-P3[k])*M4[k], M3[k] = P1[k]*tp[k]-(1-P1[k])*sl[k], M4[k] = Sum(i)(P0[i][k]*pr[i][k])-Sum(j)(P01[j][k]*ls[j][k]); Sum(i)(P0[i][k])+Sum(j)(P01[j][k]) = 1

• PS[k] - k'nıncı durma seviyesi seçeneğinin ayarlanma olasılığı
  
• MS[k] - k'nıncı durma seviyesi ile kapatılan işlemlerin beklenen getirisi
  
• M3[k] - k'nıncı stop seviyesine sahip bir durma emri ile kapanırken beklenen getiri
• M4[k] - k'nıncı stop seviyesine sahip bir sinyal emri ile kapanırken beklenen getiri
• P1[k], P2[k] - her durumda durma seviyelerinden birinin tetiklenmesi koşuluyla, durma seviyelerinin etkinleşme olasılıkları
  
• P0[i][k] - k'nıncı stop seviyesine sahip bir sinyale göre pr[i][k] kârı ile bir işlemin kapanma olasılığı. i - kapanış seçeneği numarası
  
• P01[j][k] - k'nıncı stop seviyesine sahip bir sinyale göre ls[j][k] zararı ile bir işlemin kapanma olasılığı. j - kapanış seçeneği numarası

Önceki (daha basit) denklemlerde olduğu gibi, kaotik ticaret ve makas olmaması durumunda M=0'dır. Yapabileceğiz en fazla şey stratejinin kendisini değiştirmektir, ancak stratejinin rasyonel bir temeli yoksa, tüm bu değişkenlerin dengesini değiştirirsiniz ve yine de 0 elde edersiniz. Bu istenmeyen dengeyi bozmak için, puan cinsinden herhangi bir sabit fiyat hareketi segmenti içerisinde herhangi bir yönde piyasa hareketinin olasılığını veya sabit bir süre içerisindeki beklenen fiyat hareketi getirisini bilmemiz gerekir. Giriş/çıkış noktaları buna bağlı olarak seçilir. Onları bulmayı başarırsanız, kârlı bir stratejiniz olacaktır.

Şimdi kâr faktörü denklemini oluşturalım. PF = Kâr/Zarar. Kâr faktörü, kârın zarara oranıdır. Sayı 1'i aşarsa strateji kârlıdır, aksi takdirde kârlı değildir. Bu, beklenen getiri kullanılarak yeniden tanımlanabilir. PrF = Mp/Ml. Bu, beklenen net kâr getirisinin beklenen net zarara oranı anlamına gelir. Denklemlerini yazalım.

• Mp = PS[1]*MSp[1]+PS[2]*MSp[2]+...+PS[k]*MSp[k]+...+PS[N]*MSp[N], MSp[k] = P3[k]*M3p[k]+(1-P3[k])*M4p[k], M3p[k] = P1[k]*tp[k], M4p[k] = Sum(i)(P0[i][k]*pr[i][k])
  
  
• Ml = PS[1]*MSl[1]+PS[2]*MSl[2]+...+PS[k]*MSl[k]+...+PS[N]*MSl[N], MSl[k] = P3[k]*M3l[k]+(1-P3[k])*M4l[k], M3l[k] = (1-P1[k])*sl[k], M4l[k] = Sum(j)(P01[j][k]*ls[j][k])
  

Sum(i)(P0[i][k])+Sum(j)(P01[j][k]) = 1.

• MSp[k] - k'nıncı durma seviyesi ile kapatılan işlemlerin beklenen getirisi
• MSI[k] - k'nıncı durma seviyesi ile kapatılan işlemlerin beklenen getirisi
  
• M3p[k] - k'nıncı stop seviyesine sahip bir durma emri ile kapanırken beklenen getiri
• M4p[k] - k'nıncı stop seviyesine sahip bir sinyal emri ile kapanırken beklenen getiri
• M3l[k] - k'nıncı stop seviyesine sahip bir durma emri ile kapanırken beklenen zarar
• M4l[k] - k'nıncı stop seviyesine sahip bir sinyal emri ile kapanırken beklenen zarar

Daha derin bir anlayış için, tüm olayları iç içe bir geçmiş şekilde şematik olarak göstereceğim:

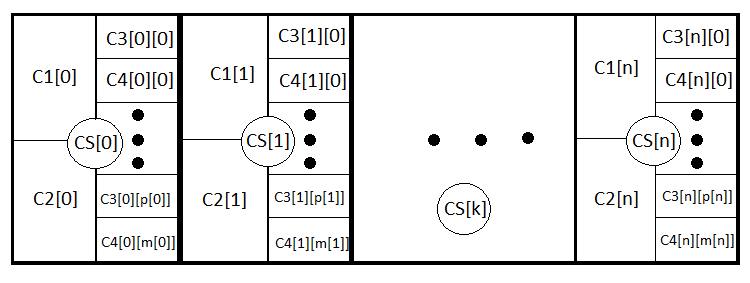
Aslında bunlar aynı denklemlerdir, ancak ilkinde zararla ilgili kısım, ikincisinde ise kârla ilgili kısım eksiktir. Kaotik ticaret durumunda, makasın yine sıfıra eşit olması koşuluyla PrF = 1 olur. M ve PrF, stratejiyi her yönden değerlendirmek için oldukça yeterli olan iki değerdir.

Özellikle, aynı olasılık teorisi ve kombinatorik kullanılarak belirli bir enstrümanın trend veya yatay yapısını değerlendirme imkanı vardır. Ayrıca, olasılık dağılım yoğunlukları yardımıyla rastgelelikten bazı farklılıklar bulmak da mümkündür.

Puan cinsinden sabit H adımında ayrıklaştırılmış bir fiyat için rastgele değer dağılımının olasılık yoğunluk grafiğini oluşturacağız. Fiyatın herhangi bir yönde H hareket etmesi halinde bir adım atılmış olduğunu varsayalım. X ekseni üzerinde rastgele bir değer olarak, grafiğin fiyat ekseni boyunca adım sayısı cinsinden ölçülen dikey hareketini çizeceğiz. Bu durumda, n adımın gerçekleşmesi gerekir, ancak o zaman genel fiyat hareketini değerlendirebiliriz.

• n - toplam adım sayısı (sabit değer)
• d - fiyat düşüşü için adım sayısı
• u - fiyat yükselişi için adım sayısı
• s - adım cinsinden nihai yukarı hareket

Bu değerleri tanımladıktan sonra u ve d değerlerini hesaplayalım:

Yukarı doğru olan nihai "s" adımını sağlamak için (değer negatif olabilir, bu da nihai hareketin aşağı doğru olduğu anlamına gelir), belirli sayıda yukarı ve aşağı adım sağlanmalıdır: "u", "d". Nihai "s" yukarı veya aşağı hareketi tüm adımlara bağlıdır:

n = u+d

s = u-d

Bu iki denklemden oluşan bir sistemdir. Çözüldüğünde u ve d elde edilir:

u = (s+n)/2, d = n-u

Ancak, tüm "s" değerleri belirli bir "n" değeri için uygun değildir. Olası s değerleri arasındaki adım her zaman 2'ye eşittir. Bu, "u" ve "d"nin doğal sayılar olmasını sağlamak için yapılır, çünkü onlar kombinatorik için veya daha doğrusu kombinasyonları hesaplamak için kullanılacaktır. Eğer bu sayılar kesirli olursa, o zaman tüm kombinatoriğin temel taşı olan faktöriyeli hesaplayamayız. Aşağıda 18 adım için tüm olası senaryolar yer almaktadır. Grafik, olay seçeneklerinin ne kadar geniş olduğunu göstermektedir.

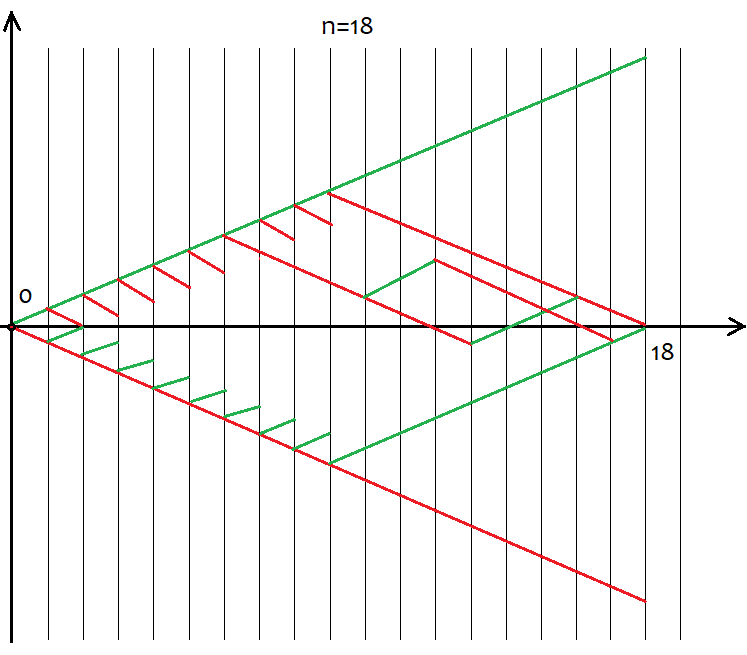
Her adımdan sonra yukarı veya aşağı olmak üzere yalnızca iki olası hareket yönü olduğundan, tüm fiyatlama varyasyonları için seçenek sayısının 2^n olduğunu tanımlamak kolaydır. Bu seçeneklerin her birini kavramaya çalışmaya gerek yoktur, çünkü bu imkansızdır. Bunun yerine sadece n adet benzersiz hücreye sahip olduğumuzu ve bunlardan u ve d’nin sırasıyla yukarı ve aşağı olması gerektiğini bilmemiz yeterlidir. Aynı u ve d'ye sahip seçenekler sonuçta aynı s'yi sağlar. Aynı "s"yi sağlayan seçeneklerin toplam sayısını hesaplamak için kombinatorikten С = n!/(u!*(n-u)!) kombinasyon formülünü ve С = n!/(d!*(n-d)!) eşdeğer formülü kullanabiliriz. Farklı u ve d durumunda, aynı C değerini elde ederiz. Kombinasyonlar hem artan hem de azalan segmentlerle yapılabildiğinden, bu kaçınılmaz olarak déjà vu'ya yol açar. Peki kombinasyonları oluşturmak için hangi segmentleri kullanmalıyız? Cevap herhangi biridir, çünkü bu kombinasyonlar farklılıklarına rağmen eşdeğerdir. Bunu aşağıda MathCad 15 tabanlı bir uygulama kullanarak kanıtlamaya çalışacağım.

Artık her senaryo için kombinasyon sayısını belirlediğimize göre, belirli bir kombinasyonun (veya olayın, nasıl isterseniz) olasılığını belirleyebiliriz. P = С/(2^n). Bu değer tüm "s"ler için hesaplanabilir ve bu olasılıkların toplamı her zaman 1'e eşittir, çünkü bu seçeneklerden biri her halükarda gerçekleşecektir. Bu olasılık dizisine dayanarak, s adımının 2 olduğunu göz önünde bulundurarak "s" rastgele değerine göre olasılık yoğunluk grafiğini oluşturabiliriz. Bu durumda, belirli bir adımdaki yoğunluk, olasılığın s adım büyüklüğüne, yani 2'ye bölünmesiyle elde edilebilir. Bunun nedeni, ayrık değerler için bir sürekli fonksiyon oluşturamamamızdır. Yoğunluk sola ve sağa doğru yarım adım, yani 1 ile ilgili kalır. Bu, düğümleri bulmamıza yardımcı olacak ve sayısal entegrasyona izin verecektir. Negatif "s" değerleri için, grafiği olasılık yoğunluk eksenine göre basitçe yansıtacağım. Çift n değerleri için düğümlerin numaralandırılması 0'dan, tek n değerleri için ise 1'den başlar. Çift n değerleri durumunda, tek s değerleri sağlayamayız, tek n değerleri durumunda da çift s değerleri sağlayamayız. Aşağıdaki hesaplama uygulaması ekran görüntüsü bunu açıklamaktadır:

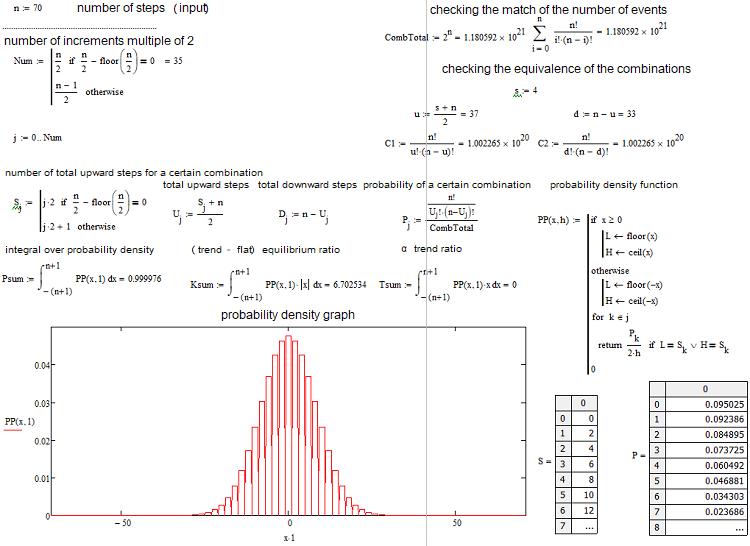
İhtiyacımız olan her şeyi listelemektedir. Parametrelerle oynayabilmeniz için uygulama aşağıya eklenmiştir. En popüler sorulardan biri, mevcut piyasa durumunun trend mi yoksa yatay mı olduğunun nasıl tanımlanacağıdır. Bir enstrümanın trend veya yatay yapısını değerlendirmek için kendi formüllerimi geliştirdim. Trendleri Alfa ve Beta olarak ikiye ayırdım. Alfa, alış ya da satış eğilimi anlamına gelirken, Beta ise alıcı ya da satıcıların açıkça tanımlanmış bir yoğunluğu olmadan hareketi sürdürme eğilimidir. Son olarak, yatay, başlangıç fiyatına geri dönme eğilimi anlamına gelir.

Trend ve yatay tanımları yatırımcılar arasında büyük farklılıklar gösterir. Ben tüm bu olgulara daha katı bir tanım getirmeye çalışıyorum, çünkü bu kavramların ve nasıl ölçüldüklerinin temel olarak anlaşılması bile daha önce ölü ya da çok basit olarak kabul edilen birçok stratejinin uygulanmasına olanak sağlayabilir. İşte bu denklemler: 

K = Integral(p*|x|)

veya

K = Sum(P[i]*|s[i]|)

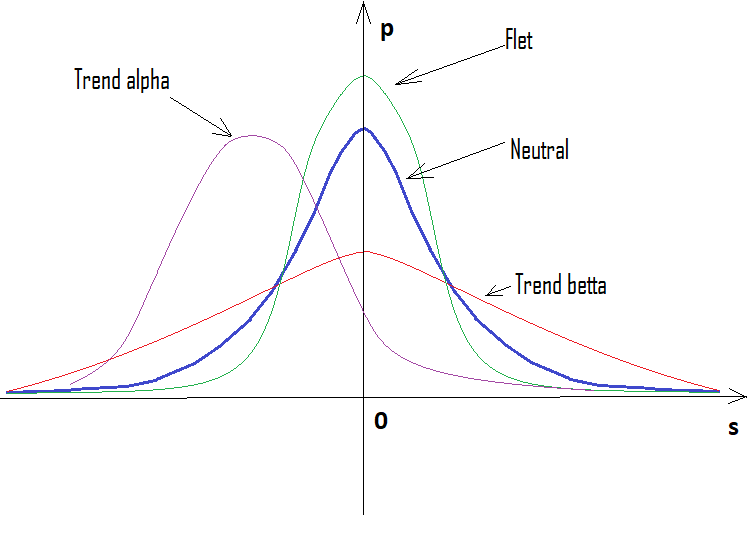
İlk seçenek bir sürekli rastgele değişken için, ikincisi ise bir ayrık değişken içindir. Daha anlaşılır olması adına ayrık değeri sürekli hale getirdim ve böylece ilk denklemi kullandım. İntegral eksi sonsuzdan artı sonsuzadır. Bu denge veya trend katsayısıdır. Bunu rastgele bir değer için hesapladıktan sonra, fiyatların gerçek dağılımını referans olanla karşılaştırmak için kullanılacak bir denge noktası elde ederiz. Eğer Кp > K ise, piyasa trend olarak kabul edilebilir. Eğer Кp < K ise, piyasa yataydır.

Katsayının maksimum değerini hesaplayabiliriz. KMax = 1*Max(|x|) veya KMax = 1*Max(|s[i]|) değerine eşittir. Ayrıca katsayının minimum değerini de hesaplayabiliriz. KMin = 1*Min(|x|) = 0 veya KMin = 1*Min(|s[i]|) = 0'a eşittir. KMid orta noktası, minimum ve maksimum, analiz edilen alanın trend veya yatay yapısını yüzde olarak değerlendirmek için gereken tek şeydir.

if (K >= KMid) KTrendPercent = ((K-KMid)/(KMax-KMid))*100 else KFletPercent = ((KMid-K)/KMid)*100

Ancak bu yine de durumu tam olarak karakterize etmek için yeterli değildir. İşte burada ikinci katsayı T = Integral(p*x), T = Sum(P[i]*s[i]) imdada yetişir. Esasen yukarı adım sayısının beklenen getirisini yansıtır ve aynı zamanda alfa trendin de bir göstergesidir. Tp > 0 alış trendi anlamına gelirken, Tp < 0 satış trendi anlamına gelir, yani T=0 rastgele yürüyüş içindir.

Katsayının maksimum ve minimum değerini bulalım: TMax = 1*Max(x) veya TMax = 1*Max(s[i]); mutlak değer olarak minimum, maksimum olana eşittir, ancak sadece negatiftir TMin = -TMax. Alfa trend yüzdesini 100'den -100'e kadar ölçersek, bir öncekine benzer şekilde bu değeri hesaplamak için denklemler yazabiliriz:

APercent = (T/TMax)*100

Yüzde pozitif ise trend yükseliş, negatif ise düşüş yönündedir. Durumlar karışık olabilir. Alfa yatay ve alfa trend olabilir ancak trend ve yatay aynı anda olamaz. Aşağıda, yukarıdaki ifadelerin grafiksel bir gösterimi ve farklı adım sayıları için oluşturulmuş yoğunluk grafiklerinin örnekleri yer almaktadır:

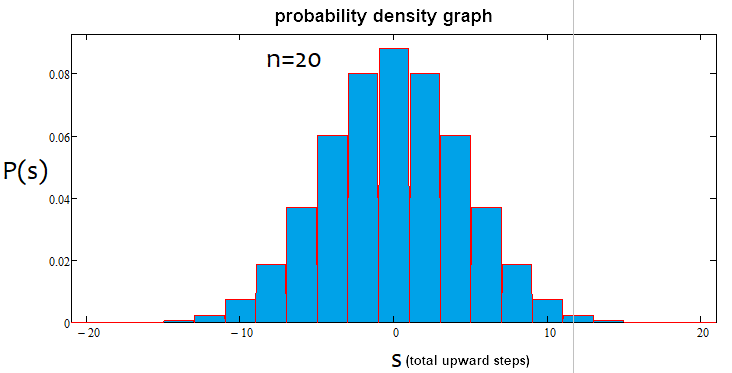
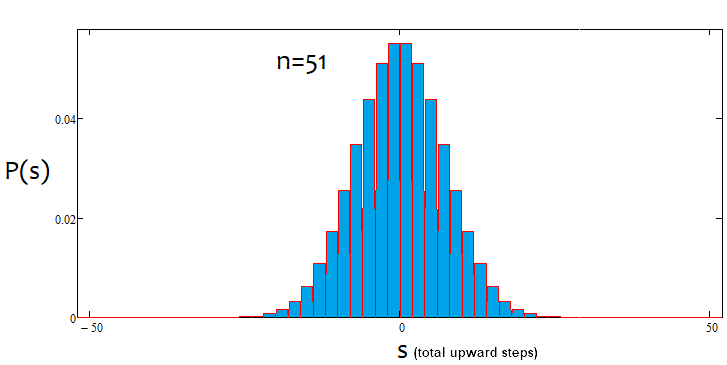
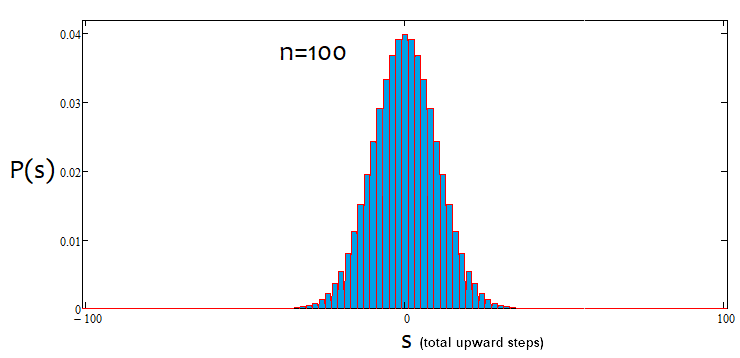
Görülebileceği gibi, adım sayısı arttıkça grafik daralmakta ve yükselmektedir. Her adım sayısı için, karşılık gelen alfa ve beta değerleri, tıpkı dağılımın kendisi gibi farklıdır. Adım sayısı değiştirilirken, referans dağılımı yeniden hesaplanmalıdır.

Tüm bu denklemler otomatik ticaret sistemleri oluşturmak için uygulanabilir. Bu algoritmalar göstergeler geliştirmek için de kullanılabilir. Bazı yatırımcılar onları Uzman Danışmanlarında halihazırda uygulamıştır. Emin olduğum bir şey vardır: bu analizden kaçınmak yerine uygulamak daha iyidir. Matematiğe aşina olanlar, onu nasıl uygulayacaklarına dair hemen yeni fikirler bulacaklardır. Aşina olmayanların ise daha fazla çaba göstermesi gerekecektir.

Basit bir gösterge yazma

Makalenin bu bölümünde basit matematiksel araştırmamızı, piyasaya giriş noktalarını tespit etmede bize yardımcı olacak ve aynı zamanda Uzman Danışmanlar yazmak için bir temel oluşturacak bir göstergeye dönüştüreceğiz. Göstergeyi MQL5'te geliştireceğiz. Ancak, kodu mümkün olan en geniş ölçüde MQL4'e taşınabilecek şekilde uyarlayacağız. Genel olarak, mümkün olan en basit metotları kullanmaya çalışıyorum ve yalnızca kod gereksiz yere hantal ve okunamaz hale gelirse OOP'ye başvuruyorum. Ancak %90 şekilde ondan kaçınmayı başarıyorum. Gereksiz renkli paneller, düğmeler ve çok miktarda veri sadece görsel algıyı engeller. Bunun yerine, her zaman mümkün olduğunca az görsel araç kullanmayı tercih ediyorum.

Göstergenin girdi parametreleriyle başlayalım.

input uint BarsI=990;//Bars TO Analyse ( start calc. & drawing )
input uint StepsMemoryI=2000;//Steps In Memory
input uint StepsI=40;//Formula Steps
input uint StepPoints=30;//Step Value
input bool bDrawE=true;//Draw Steps

Gösterge grafiğe eklendiğinde, belirli miktarda son mumu temel alarak belirli sayıda adımdan oluşan bir başlangıç hesaplaması yapabiliriz. Son adımlarımızla ilgili verileri depolamak için de bir arabelleğe ihtiyacımız olacaktır. Böylece, yeni veriler eskilerinin yerini alacaktır. Büyüklüğü sınırlı olmalıdır. Aynı büyüklük, adımları grafik üzerinde çizmek için de kullanılacaktır. Göstergeye dağılımı kaç adımda oluşturacağımızı söylemeli ve gerekli değerleri hesaplamalıyız. Daha sonra sisteme puan cinsinden adım büyüklüğünü ve adımların görselleştirilmesine ihtiyacımız olup olmadığını söylemeliyiz. Adımlar grafik üzerinde çizilerek görselleştirilecektir.

Nötr dağılımı ve mevcut durumu gösteren ayrı bir pencere şeklinde gösterge stilini seçtim. İki çizgi vardır, ancak grafikte üçüncü bir çizginin olması iyi olurdu. Ne yazık ki, göstergenin yetenekleri ayrı ve ana pencerede çizime izin vermiyor, bu yüzden böyle devam etmek zorunda kaldım.

MQL4'te olduğu gibi çubuk verilerine erişebilmek için her zaman aşağıdaki küçük püf noktasını kullanıyorum:

//variable to be moved in MQL5
double Close[];
double Open[];
double High[];
double Low[];
long Volume[];
datetime Time[];
double Bid;
double Ask;
double Point=_Point;
int Bars=1000;
MqlTick TickAlphaPsi;

void DimensionAllMQL5Values()//set the necessary array size
   {
   ArrayResize(Close,BarsI,0);
   ArrayResize(Open,BarsI,0);   
   ArrayResize(Time,BarsI,0);
   ArrayResize(High,BarsI,0);
   ArrayResize(Low,BarsI,0);
   ArrayResize(Volume,BarsI,0);
   }

void CalcAllMQL5Values()//recalculate all arrays
   {
   ArraySetAsSeries(Close,false);                        
   ArraySetAsSeries(Open,false);                           
   ArraySetAsSeries(High,false);                        
   ArraySetAsSeries(Low,false);                              
   ArraySetAsSeries(Volume,false);
   ArraySetAsSeries(Time,false);                                                            
   if( Bars >= int(BarsI) ) 
      {
      CopyClose(_Symbol,_Period,0,BarsI,Close);
      CopyOpen(_Symbol,_Period,0,BarsI,Open);   
      CopyHigh(_Symbol,_Period,0,BarsI,High);
      CopyLow(_Symbol,_Period,0,BarsI,Low);
      CopyTickVolume(_Symbol,_Period,0,BarsI,Volume); 
      CopyTime(_Symbol,_Period,0,BarsI,Time);      
      }
   ArraySetAsSeries(Close,true);
   ArraySetAsSeries(Open,true);
   ArraySetAsSeries(High,true);                        
   ArraySetAsSeries(Low,true);
   ArraySetAsSeries(Volume,true);                                                                                                
   ArraySetAsSeries(Time,true);
   SymbolInfoTick(Symbol(),TickAlphaPsi);
   Bid=TickAlphaPsi.bid;
   Ask=TickAlphaPsi.ask;
   }
////////////////////////////////////////////////////////////

Artık kod mümkün olduğunca MQL4 ile uyumlu hale geldi. Hızlı ve kolay bir şekilde MQL4 analoğuna dönüştürülebilir.

Devam edelim. Adımları tanımlamak için öncelikle düğümleri tanımlamamız gerekiyor.

struct Target//structure for storing node data
   {
   double Price0;//node price
   datetime Time0;//node price
   bool Direction;//direction of a step ending at the current node
   bool bActive;//whether the node is active
   };
   
double StartTick;//initial tick price
Target Targets[];//destination point ticks (points located from the previous one by StepPoints)

Ek olarak, bir sonraki adımı saymak için bir noktaya ihtiyacımız olacaktır. Düğüm, kendisi ve üzerinde sona eren adım hakkındaki verilerin yanı sıra düğümün aktif olup olmadığını gösteren boolean bileşenini de depolar. Yalnızca düğüm dizisinin tüm belleği gerçek düğümlerle doldurulduğunda gerçek dağılım hesaplanacaktır, çünkü gerçek dağılım adımlarla hesaplanır. Adım yoksa hesaplama da yok demektir.

Ayrıca, her adımda adımların durumunu güncelleme ve göstergeyi başlatırken çubuklara göre yaklaşık bir hesaplama yapma yeteneğine sahip olmamız gerekir.

bool UpdatePoints(double Price00,datetime Time00)//update the node array and return 'true' in case of a new node
   {
   if ( MathAbs(Price00-StartTick)/Point >= StepPoints )//if the step size reaches the required one, write it and 
shift the array back
      {
      for(int i=ArraySize(Targets)-1;i>0;i--)//first move everything back
         {
         Targets[i]=Targets[i-1];
         }
      //after that, generate a new node  
      Targets[0].bActive=true;
      Targets[0].Time0=Time00;
      Targets[0].Price0=Price00;
      Targets[0].Direction= Price00 > StartTick ? true : false;
      //finally, redefine the initial tick to track the next node
      StartTick=Price00;
      return true;
      }
   else return false;
   }

void StartCalculations()//approximate initial calculations (by bar closing prices)
   {
   for(int j=int(BarsI)-2;j>0;j--) 
      {
      UpdatePoints(Close[j],Time[j]);
      }  
   }

Ardından, tüm nötr çizgisi parametrelerini hesaplamak için gerekli olan metotları ve değişkenleri tanımlayalım. Ordinatı, belirli bir kombinasyonun veya sonucun olasılığını temsil eder. Buna normal dağılım demekten hoşlanmıyorum çünkü normal dağılım sürekli bir niceliktir, biz ise burada ayrık bir değerin grafiğini oluşturuyoruz. Ayrıca, normal dağılım, göstergede olduğu gibi bir olasılık yerine bir olasılık yoğunluğudur. Bu durumda, yoğunluğu yerine bir olasılık grafiği oluşturmak daha uygundur.

int S[];//array of final upward steps
int U[];//array of upward steps
int D[];//array of downward steps
double P[];//array of particular outcome probabilities

double KBettaMid;//neutral Betta ratio value
double KBettaMax;//maximum Betta ratio value
//minimum Betta = 0, there is no point in setting it
double KAlphaMax;//maximum Alpha ratio value
double KAlphaMin;//minimum Alpha ratio value
//average Alpha = 0, there is no point in setting it

int CalcNumSteps(int Steps0)//calculate the number of steps
   {
   if ( Steps0/2.0-MathFloor(Steps0/2.0) == 0 ) return int(Steps0/2.0);
   else return int((Steps0-1)/2.0);
   }

void ReadyArrays(int Size0,int Steps0)//prepare the arrays
   {
   int Size=CalcNumSteps(Steps0);
   ArrayResize(S,Size);
   ArrayResize(U,Size);
   ArrayResize(D,Size);
   ArrayResize(P,Size);
   ArrayFill(S,0,ArraySize(S),0);//clear
   ArrayFill(U,0,ArraySize(U),0);
   ArrayFill(D,0,ArraySize(D),0);
   ArrayFill(P,0,ArraySize(P),0.0);
   }

void CalculateAllArrays(int Size0,int Steps0)//calculate all arrays
   {
   ReadyArrays(Size0,Steps0);
   double CT=CombTotal(Steps0);//number of combinations
   for(int i=0;i<ArraySize(S);i++)
      {
      S[i]=Steps0/2.0-MathFloor(Steps0/2.0) == 0 ? i*2 : i*2+1 ;
      U[i]=int((S[i]+Steps0)/2.0);
      D[i]=Steps0-U[i];
      P[i]=C(Steps0,U[i])/CT;
      }
   }

void CalculateBettaNeutral()//calculate all Alpha and Betta ratios
   {
   KBettaMid=0.0;
   if ( S[0]==0 )
      {
      for(int i=0;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(S[i])*P[i];
         }
      for(int i=1;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(-S[i])*P[i];
         }
      }
   else
      {
      for(int i=0;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(S[i])*P[i];
         }
      for(int i=0;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(-S[i])*P[i];
         }
      }
   KBettaMax=S[ArraySize(S)-1];
   KAlphaMax=S[ArraySize(S)-1];
   KAlphaMin=-KAlphaMax;
   }
   
double Factorial(int n)//factorial of n value
   {
   double Rez=1.0;
   for(int i=1;i<=n;i++)
      {
      Rez*=double(i);
      }
   return Rez;
   }
   
double C(int n,int k)//combinations from n by k
   {
   return Factorial(n)/(Factorial(k)*Factorial(n-k));
   }
   
double CombTotal(int n)//number of combinations in total
   {
   return MathPow(2.0,n);
   }

Tüm bu fonksiyonlar doğru yerde çağrılmalıdır. Buradaki tüm fonksiyonlar, ilk ikisi hariç, ya dizilerin değerlerini hesaplamaya yöneliktir ya da bazı yardımcı matematiksel fonksiyonları uygulamak içindir. Nötr dağılımın hesaplanmasıyla birlikte başlatma sırasında çağrılırlar ve dizilerin büyüklüğünü ayarlamak için kullanılırlar.

Devamında, gerçek dağılımı ve ana parametrelerini aynı şekilde hesaplamak için bir kod bloğu oluşturalım.

double AlphaPercent;//alpha trend percentage
double BettaPercent;//betta trend percentage
int ActionsTotal;//total number of unique cases in the Array of steps considering the number of steps for checking the option
int Np[];//number of actual profitable outcomes of a specific case
int Nm[];//number of actual losing outcomes of a specific case
double Pp[];//probability of a specific profitable step
double Pm[];//probability of a specific losing step
int Sm[];//number of losing steps

void ReadyMainArrays()//prepare the main arrays
   {
   if ( S[0]==0 )
      {
      ArrayResize(Np,ArraySize(S));
      ArrayResize(Nm,ArraySize(S)-1);
      ArrayResize(Pp,ArraySize(S));
      ArrayResize(Pm,ArraySize(S)-1);      
      ArrayResize(Sm,ArraySize(S)-1);
      for(int i=0;i<ArraySize(Sm);i++)
         {
         Sm[i]=-S[i+1];
         }
      ArrayFill(Np,0,ArraySize(Np),0);//clear
      ArrayFill(Nm,0,ArraySize(Nm),0);
      ArrayFill(Pp,0,ArraySize(Pp),0);
      ArrayFill(Pm,0,ArraySize(Pm),0);      
      }
   else
      {
      ArrayResize(Np,ArraySize(S));
      ArrayResize(Nm,ArraySize(S));
      ArrayResize(Pp,ArraySize(S));
      ArrayResize(Pm,ArraySize(S));      
      ArrayResize(Sm,ArraySize(S));
      for(int i=0;i<ArraySize(Sm);i++)
         {
         Sm[i]=-S[i];
         }
      ArrayFill(Np,0,ArraySize(Np),0);//clear
      ArrayFill(Nm,0,ArraySize(Nm),0);
      ArrayFill(Pp,0,ArraySize(Pp),0);
      ArrayFill(Pm,0,ArraySize(Pm),0);            
      }   
   }

void CalculateActionsTotal(int Size0,int Steps0)//total number of possible outcomes made up of the array of steps
   {
   ActionsTotal=(Size0-1)-(Steps0-1);
   }

bool CalculateMainArrays(int Steps0)//count the main arrays
   {
   int U0;//upward steps
   int D0;//downward steps
   int S0;//total number of upward steps
   if ( Targets[ArraySize(Targets)-1].bActive )
      {
      ArrayFill(Np,0,ArraySize(Np),0);//clear
      ArrayFill(Nm,0,ArraySize(Nm),0);
      ArrayFill(Pp,0,ArraySize(Pp),0);
      ArrayFill(Pm,0,ArraySize(Pm),0);      
      for(int i=1;i<=ActionsTotal;i++)
         {
         U0=0;
         D0=0;
         S0=0;
         for(int j=0;j<Steps0;j++)
            {
            if ( Targets[ArraySize(Targets)-1-i-j].Direction ) U0++;
            else D0++;
            }
         S0=U0-D0;
         
         for(int k=0;k<ArraySize(S);k++)
            {
            if ( S[k] == S0 )
               {
               Np[k]++;
               break;
               }
            }
         for(int k=0;k<ArraySize(Sm);k++)
            {
            if ( Sm[k] == S0 )
               {
               Nm[k]++;
               break;
               }
            }
         }
         
      for(int k=0;k<ArraySize(S);k++)
         {
         Pp[k]=Np[k]/double(ActionsTotal);
         }
      for(int k=0;k<ArraySize(Sm);k++)
         {
         Pm[k]=Nm[k]/double(ActionsTotal);
         }         
         
      AlphaPercent=0.0;
      BettaPercent=0.0;
      for(int k=0;k<ArraySize(S);k++)
         {
         AlphaPercent+=S[k]*Pp[k];
         BettaPercent+=MathAbs(S[k])*Pp[k];
         }
      for(int k=0;k<ArraySize(Sm);k++)
         {
         AlphaPercent+=Sm[k]*Pm[k];
         BettaPercent+=MathAbs(Sm[k])*Pm[k];
         }
      AlphaPercent= (AlphaPercent/KAlphaMax)*100;
      BettaPercent= (BettaPercent-KBettaMid) >= 0.0 ? ((BettaPercent-KBettaMid)/(KBettaMax-KBettaMid))*100 : ((BettaPercent-KBettaMid)/KBettaMid)*100;
      
      Comment(StringFormat("Alpha = %.f %%\nBetta = %.f %%",AlphaPercent,BettaPercent));//display these numbers on the screen
      return true;
      }
   else return false;
   }

Burada her şey benzerdir ancak grafik her zaman dikey eksene göre yansıtılmayacağından çok daha fazla dizi vardır. Bu amaçla ek dizilere ve değişkenlere ihtiyacımız vardır, ancak genel olarak mantık basittir: belirli olgu sonuçlarının sayısını hesaplayalım ve bunu tüm sonuçların toplam sayısına bölelim. Bu şekilde tüm olasılıkları (ordinatlar) ve bunlara karşılık gelen apsisleri elde ederiz. Her bir döngüye ve değişkene girmeyeceğim. Tüm bu karmaşıklıklar, değerlerin arabelleklere taşınmasıyla ilgili sorunları önlemek için gereklidir. Burada her şey neredeyse aynıdır: dizilerin büyüklüğünü tanımlıyoruz ve onları sayıyoruz. Ardından, alfa ve beta trend yüzdelerini hesaplıyoruz ve onları ekranın sol üst köşesinde görüntülüyoruz.

Geriye neyi nerede çağıracağımızı belirlemek kalıyor.

int OnInit()
  {
   //--- indicator buffers mapping
   SetIndexBuffer(0,NeutralBuffer,INDICATOR_DATA);
   SetIndexBuffer(1,CurrentBuffer,INDICATOR_DATA);
   CleanAll();
   DimensionAllMQL5Values();
   CalcAllMQL5Values();
   StartTick=Close[BarsI-1];
   ArrayResize(Targets,StepsMemoryI);//maximum number of nodes
   CalculateAllArrays(StepsMemoryI,StepsI);
   CalculateBettaNeutral();
   StartCalculations();
   ReadyMainArrays();
   CalculateActionsTotal(StepsMemoryI,StepsI);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  CalcAllMQL5Values();
  
  if ( UpdatePoints(Close[0],TimeCurrent()) )
     {
     if ( CalculateMainArrays(StepsI) )
        {
        if ( bDrawE ) RedrawAll();
        }
     }
      
  int iterator=rates_total-(ArraySize(Sm)+ArraySize(S))-1;
  for(int i=0;i<ArraySize(Sm);i++)
     {
     iterator++;
     NeutralBuffer[iterator]=P[ArraySize(S)-1-i];
     CurrentBuffer[iterator]=Pm[ArraySize(Sm)-1-i];
     }
  for(int i=0;i<ArraySize(S);i++)
     {
     iterator++;
     NeutralBuffer[iterator]=P[i];
     CurrentBuffer[iterator]=Pp[i];
     }

   return(rates_total);
  }

CurrentBuffer ve NeutralBuffer burada arabellek olarak kullanılmaktadır. Daha anlaşılır olması adına, gösterimi piyasaya en yakın mum çubukları üzerinde yaptım. Her olasılık ayrı bir çubuk üzerindedir. Bu da gereksiz komplikasyonlardan kurtulmamızı sağladı. Her şeyi görmek için grafiği yakınlaştırıp uzaklaştırmamız yeterlidir. CleanAll() ve RedrawAll() fonksiyonları burada gösterilmemiştir. Onlar yorum olarak hariç tutulabilir ve her şey render edilmeden sorunsuz çalışacaktır. Ayrıca, çizim bloğunu da buraya dahil etmedim. Ekte bulabilirsiniz. Orada kayda değer bir şey yoktur. Gösterge ayrıca aşağıda iki versiyonda eklenmiştir - MetaTrader 4 ve MetaTrader 5 için.

Aşağıdaki gibi görünecektir:

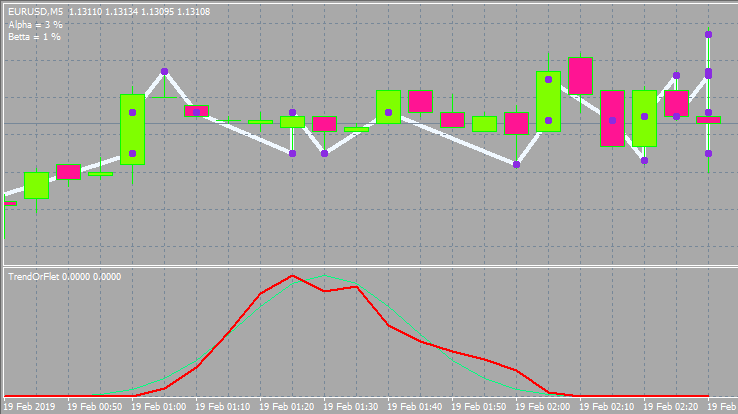
Aşağıda farklı girdiler ve pencere stiliyle bir alternatif bulunmaktadır:

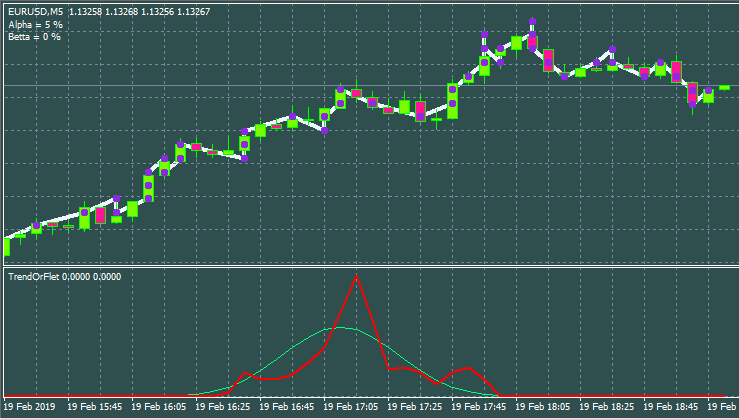
En ilginç stratejilerin gözden geçirilmesi

Pek çok strateji geliştirdim ve gördüm. Naçizane tecrübelerime göre, en göze çarpan şeyler grid veya martingale ya da her ikisi birden kullanıldığında gerçekleşmektedir. Ancak açık konuşmak gerekirse, hem martingale hem de grid'in beklenen getirisi 0'dır. Yukarı doğru giden grafiklere aldanmayın çünkü bir gün büyük bir kayıp yaşayacaksınız. Çalışan gridler vardır ve piyasada bulunabilirler. Oldukça iyi çalışırlar ve hatta 3-6 kâr faktörü gösterirler. Bu oldukça yüksek bir değerdir. Dahası, herhangi bir döviz çiftinde stabil olarak çalışırlar. Ancak kazanmanızı sağlayacak filtreler bulmak kolay değildir. Yukarıda açıklanan yöntem bu sinyalleri ayırmanıza olanak tanır. Grid bir trend gerektirir, ancak yön önemli değildir. 

Martingale ve grid en basit ve popüler strateji örnekleridir. Ancak, herkes onları doğru şekilde uygulayamaz. Kendi kendini uyarlayan Uzman Danışmanlar biraz daha karmaşıktır. Yatay, trend veya başka herhangi bir model olsun, her şeye uyum sağlayabilirler. Genellikle piyasanın belirli bir parçasını alıp modelleri aramayı ve modelin bir süre daha devam edeceği umuduyla kısa bir süre boyunca ticaret yapmayı içerirler.

Ayrı bir grup, piyasanın kaotik doğasından kâr elde etmeye çalışan gizemli, alışılmadık algoritmalara sahip egzotik sistemler tarafından oluşturulmuştur. Bu tür sistemler saf matematiğe dayanır ve herhangi bir enstrüman ve zaman diliminde kâr elde edebilir. Kâr büyük değildir ama istikrarlıdır. Son zamanlarda bu tür sistemlerle uğraşıyorum. Bu grupta brute force’a dayalı robotlar da yer almaktadır. Brute force ek yazılım kullanılarak gerçekleştirilebilir. Bir sonraki makalede, böyle bir programın bir versiyonunu göstereceğim.

En üst sırada sinir ağlarına ve benzer yazılımlara dayalı robotlar yer almaktadır. Bu robotlar çok farklı sonuçlar gösterir ve sinir ağı yapay zekanın bir prototipi olduğu için en üst düzeyde karmaşıklığa sahiptir. Bir sinir ağı uygun şekilde geliştirilir ve eğitilirse, başka hiçbir stratejiyle kıyaslanamayacak kadar yüksek verimlilik gösterebilir.

Değerlendirmeye gelince, bana göre, artık olasılıkları neredeyse sıfıra eşittir. Hiçbir sonuç vermeyen Uzman Danışmanlarım vardır.

Bu zahmete değer mi?

Birisi heyecan duyduğu için piyasalarda ticaret yapar, birisi kolay ve hızlı para arar, birisi ise denklemler ve teoriler yoluyla piyasa süreçlerini incelemek ister. Ayrıca, kendileri için geri dönüş yolu olmadığı için başka seçeneği olmayan yatırımcılar da vardır. Ben çoğunlukla ikinci kategoriye aitim. Tüm bilgi ve deneyimime rağmen, şu anda kârlı ve istikrarlı bir hesabım yok. İyi test çalışmaları gösteren Uzman Danışmanlarım var ama her şey göründüğü kadar kolay değildir.

Hızlı bir şekilde zengin olmaya çalışanlar büyük olasılıkla tam tersi bir sonuçla karşılaşacaklardır. Sonuçta, piyasa sıradan bir yatırımcının kazanması için yaratılmamıştır. Bunun tam tersi bir amacı vardır. Ancak, bu konuya girecek kadar cesursanız, bolca zamanınız ve sabrınız olduğundan emin olun. Sonuç hızlı olmayacaktır. Programlama beceriniz yoksa, neredeyse hiç şansınız yok demektir. 20-30 işlem yaptıktan sonra bazı sonuçlar hakkında övünen birçok sözde yatırımcı gördüm. Benim durumumda, iyi bir Uzman Danışman geliştirdikten sonra, bir veya iki yıl çalışabilmektedir ama sonrasında kaçınılmaz olarak başarısız olmaktadır... Çoğu durumda da başlangıçtan itibaren çalışmamaktadır.

Elbette manuel ticaret diye bir şey vardır ama ben bunun daha çok sanata benzediğine inanıyorum. Sonuç olarak, piyasada para kazanmak mümkündür, ancak çok zaman harcamanız gerekmektedir. Şahsen ben buna değeceğini düşünmüyorum. Matematiksel açıdan bakıldığında, piyasa sadece sıkıcı iki boyutlu bir eğridir. Kesinlikle hayatım boyunca mumlara bakmak istemiyorum.

Kutsal kase var mı ve nerede aranmalı?

Kutsal kasenin mümkün olduğuna inanıyorum. Bunu kanıtlayan nispeten basit Uzman Danışmanlarım vardır. Ne yazık ki, beklenen getirileri makası ancak karşılamaktadır. Neredeyse her geliştiricinin bunu doğrulayan stratejileri olduğunu düşünüyorum. Piyasada her açıdan kutsal kase olarak adlandırılabilecek çok sayıda robot vardır. Ancak bu tür sistemlerle para kazanmak son derece zordur çünkü her pip için mücadele etmeniz, ayrıca makas iadelerini ve ortaklık programlarını etkinleştirmeniz gerekir. Önemli kârlar ve düşük mevduat yükleri içeren kutsal kaseler nadirdir.

Eğer kendi başınıza bir kutsal kase geliştirmek istiyorsanız, o zaman sinir ağlarına bakmanız daha iyi olacaktır. Kâr açısından çok fazla potansiyele sahiplerdir. Elbette, çeşitli egzotik yaklaşımları ve brute force’u kombine etmeyi deneyebilirsiniz, ancak hemen sinir ağlarını araştırmanızı tavsiye ederim.

İşin tuhafı, bir kutsal kasenin var olup olmadığı ve nerede aranacağı sorularının cevabı, geliştirdiğim tonlarca Uzman Danışmandan sonra benim için oldukça basit ve açıktır.

Yatırımcılar için ipuçları

Tüm yatırımcılar şu üç şeyi ister:

• Pozitif beklenen getiri elde etmek
• Kârda olan bir pozisyon durumunda kârı artırmak
• Zararda olan bir pozisyon durumunda zararı azaltmak

İlk madde burada en önemli olanıdır. Kârlı bir stratejiniz varsa (manuel veya algoritmik olmasına bakılmaksızın), her zaman müdahale etmek isteyeceksiniz. Buna izin verilmemelidir. Kârda olan işlemlerin zararda olan işlemlerden daha az sayıda olduğu durumlar, bir ticaret sistemini bozan önemli bir psikolojik etki yaratır. En önemlisi, kırmızıdayken kayıplarınızı geri kazanmak için acele etmeyin. Aksi takdirde, kendinizi daha da fazla kayıpla karşı karşıya bulabilirsiniz. Beklenen getiriyi hatırlayın. Mevcut pozisyonun varlık kaybının ne olduğu önemli değildir. Asıl önemli olan toplam pozisyon sayısı ve kâr/zarar oranıdır.

Bir sonraki önemli konu, ticaretinizde uyguladığınız lot büyüklüğüdür. Şu anda kâr ediyorsanız, lotu kademeli olarak azalttığınızdan emin olun. Tersi durumda ise artırın. Ancak, sadece belirli bir eşik değerine kadar artırılmalıdır. Bu bir ileri ve geri martingale’dir. Dikkatli düşünürseniz, tamamen lot varyasyonlarına dayalı olarak kendi Uzman Danışmanlarınızı geliştirebilirsiniz. Bu artık bir grid veya martingale değil, daha karmaşık ve güvenli bir şey olacaktır. Ayrıca, böyle bir Uzman Danışman, fiyat geçmişi boyunca tüm döviz çiftleri üzerinde çalışabilir. Bu ilke kaotik bir piyasada bile işe yarar ve nereye ve nasıl girdiğiniz önemli değildir. Doğru kullanımla, tüm makasları ve komisyonları kompanse edersiniz ve ustaca kullanımla, piyasaya rastgele bir noktada ve rastgele bir yönde girseniz bile kâr elde edersiniz.

Zararları azaltmak ve kârı artırmak için negatif yarım dalgada alış yapmaya ve pozitif yarım dalgada da satış yapmaya çalışın. Bir yarım dalga genellikle alıcıların veya satıcıların bu alanda aktif olduğunu gösterir, bu da bazılarının halihazırda piyasada olduğu ve açık pozisyonların er ya da geç kapanacağı ve bu da fiyatı ters yönde hareket ettireceği anlamına gelir. Bu yüzden piyasa dalga yapısına sahiptir. Bu dalgaları her yerde görebiliriz. Bir alışı bir satış takip eder ve bunun tersi de geçerlidir. Aynı kriteri kullanarak pozisyonlarınızı da kapatın.

Sonuç

Herkesin bakış açısı özneldir. Sonuçta, öyle ya da böyle, her şey size bağlıdır. Tüm dezavantajlarına ve boşa harcanan zamana rağmen, herkes kendi süper sistemini oluşturmak ve kararlılığın meyvelerini toplamak ister. Aksi takdirde, Forex ticaretine girmenin bir mantığı olduğunu düşünmüyorum. Bu faaliyet bir şekilde ben de dahil olmak üzere birçok yatırımcı için cazibesini korumaktadır. Herkes bu duygunun nasıl adlandırıldığını bilir, ancak kulağa çocukça gelecektir. Bu nedenle, trolü önlemek adına söylemeyeceğim.