Teoria das Categorias (Parte 9): Ações dos monoides

Introdução

No artigo anterior, apresentamos os monoides e vimos como eles podem ser usados no aprendizado supervisionado para classificar e informar decisões de negociação. Para continuar, exploraremos as ações de monoides e como elas também podem ser usadas no aprendizado não supervisionado para reduzir dimensões nos dados de entrada. As saídas dos monoides de suas operações sempre resultam em membros de seu conjunto, o que significa que elas não são transformadoras. Assim, são as ações de monoides que adicionam a capacidade de transformação, uma vez que o conjunto de ações não precisa ser um subconjunto do conjunto monoidal. Por transformação, queremos dizer a capacidade de ter saídas de ação que não são membros do conjunto monoidal.

Formalmente, uma ação monoidal a de um monoide M (e, *) em um conjunto S é definida como:

a: M x S - - > S ;                                (1)

e a s - - > s;                                      (2)

m * (n * s) - - > (m * n) a s                (3)

Onde m, n são membros do monoide M, e s é um membro do conjunto S.

Ilustração e métodos

Compreender a importância relativa de diferentes recursos no processo de tomada de decisão de um modelo é valioso. Em nosso caso, como mencionado no artigo anterior, nossos 'parâmetros' foram:

• Período de análise retrospectiva
• Período
• Preço aplicável
• Indicador
• E a decisão de negociar em uma faixa ou tendência.

Vamos analisar alguns métodos que são aplicáveis para ponderar as funções do nosso modelo e ajudar a identificar o mais sensível à precisão de nossa previsão. Selecionaremos um método e, com base em sua recomendação, procuraremos adicionar uma transformação ao monoide nesse nó, expandindo o conjunto monoidal por meio de ações de monoides, e veremos qual efeito isso tem em nossa capacidade de colocar trailing stops com precisão, conforme a aplicação que consideramos no artigo anterior.

Ao determinar a importância relativa de cada coluna de dados em um conjunto de treinamento, existem várias ferramentas e métodos que podem ser empregados. Esses métodos ajudam a quantificar a contribuição de cada função (coluna de dados) para as previsões do modelo e nos orientam sobre qual coluna de dados talvez precise ser detalhada e qual deve receber menos atenção. Aqui estão alguns métodos comumente usados:

Classificação de importância do parâmetro

Esta abordagem classifica os recursos com base na importância, considerando o impacto no desempenho do modelo. Normalmente, vários algoritmos, como Random Forests, Gradient Boosting Machines ou árvores aditivas, fornecem medidas incorporadas a nível de importância de características que não só ajudam na construção de árvores, mas também podem ser extraídas após o treinamento do modelo.

Para ilustrar isso, vamos considerar um cenário em que, como no artigo anterior, desejamos prever mudanças no intervalo de preços e usar isso para ajustar o trailing stop das posições abertas. Assim sendo, estaremos considerando os pontos de decisão que tínhamos naquele momento (funções ou colunas de dados) como árvores. Se usarmos um classificador floresta aleatória para essa tarefa, considerando cada um dos nossos pontos de decisão como uma árvore, após o treinamento do modelo, podemos extrair a classificação de importância dos parâmetros.

Para esclarecer, nosso conjunto de dados conterá as seguintes árvores:

• Duração do período de análise retrospectiva (dados inteiros)
• Período selecionado para negociação (dados de enumeração: H1, H2, H3, etc.)
• Preço aplicável usado na análise (dados de enumeração: preço de abertura, preço médio, preço típico, preço de fechamento)
• Seleção do indicador usado na análise (dados de enumeração do oscilador RSI ou envelopes de bandas de Bollinger)

Após o treinamento com o classificador de floresta aleatória, podemos extrair a classificação de importância dos parâmetros usando pesos de impureza de Gini (Gini impurity weights). As pontuações de importância dos parâmetros indicam a importância relativa (ponderação) de cada coluna de dados no processo de tomada de decisão do modelo.

Vamos supor que a classificação de importância dos parâmetros resultou no seguinte:

• Seleção do indicador usado na análise: 0,45
• Duração do período de análise retrospectiva: 0.30
• Preço aplicável: 0.20
• Período gráfico: 0.05

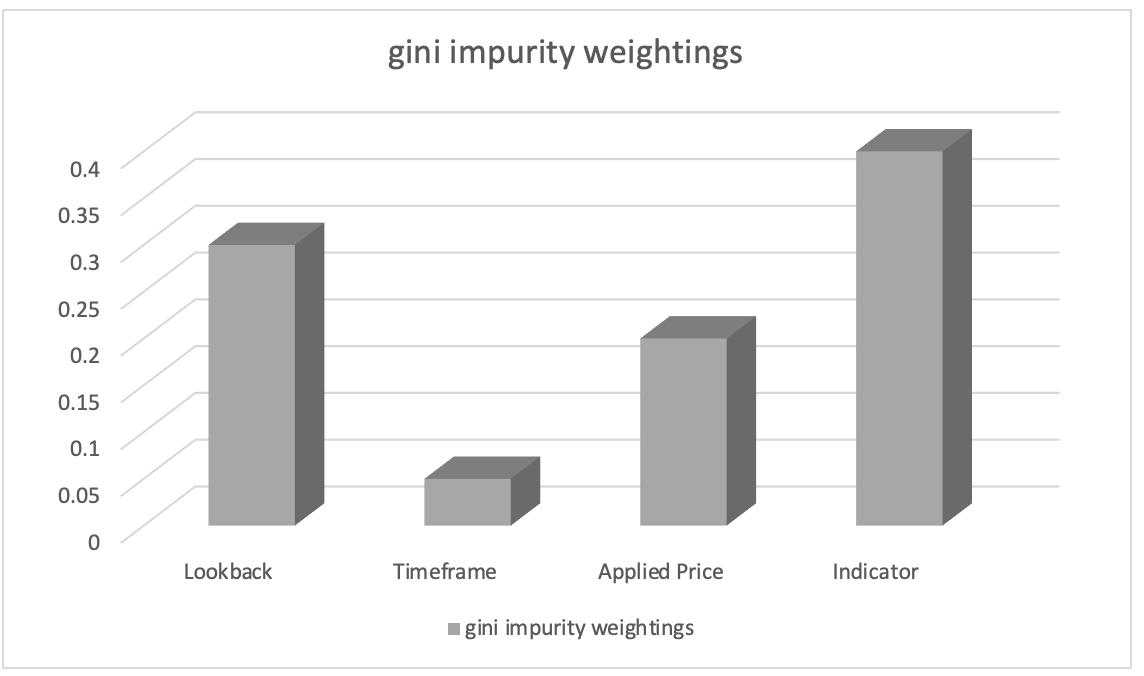
Com base nisso, podemos inferir que o parâmetro "Escolha do indicador usado na análise" tem a maior importância, seguido pelo parâmetro "Período de análise retrospectiva". O parâmetro "Preço aplicado na análise" é classificado em terceiro lugar, enquanto o parâmetro "Prazo escolhido na negociação" tem a menor importância.

Essas informações podem nos orientar a entender quais parâmetros são mais significativos na influência das previsões do modelo e, com esse conhecimento, poderíamos nos concentrar em parâmetros mais importantes durante a engenharia de parâmetros, priorizar a seleção de parâmetros ou explorar informações adicionais específicas do domínio relacionadas a esses parâmetros. Em nosso caso, poderíamos examinar a transformação do conjunto monoidal de indicadores, introduzindo conjuntos de ação monoidais de outros indicadores e examinando como isso influencia nossas previsões. Desse modo, nossos conjuntos de ação adicionariam indicadores alternativos ao oscilador RSI e à Bollinger Bands Envelope. No entanto, qualquer indicador que adicionemos, como foi o caso das Bollinger Bands no artigo anterior, precisaríamos regularizar sua saída e garantir que esteja na faixa de 0 a 100, com 0 indicando uma diminuição no intervalo de barras de preço, enquanto 100 indica um aumento no intervalo.

Importância da permutação

O teste de aleatorização avalia a importância da ordem dos parâmetros (ou colunas de dados) ao permutar aleatoriamente sua ordem e medir a subsequente alteração no desempenho do modelo ao fazer previsões. Lembre-se de que a ordem até agora tem sido o período de análise retrospectiva, o período gráfico, o preço aplicado, o indicador e, finalmente, o tipo de decisão de negociação. O que aconteceria se organizássemos nossas decisões de maneira diferente? Teríamos que fazer isso permutando apenas uma coluna de dados (parâmetro) de cada vez. Uma queda maior na precisão das previsões para uma dessas colunas de dados indicaria maior importância. Este método é independente do modelo e pode ser aplicado a qualquer algoritmo de aprendizado de máquina.

Para ilustrar isso, vamos considerar um cenário com nosso mesmo conjunto de dados de cinco colunas, como mencionado acima e no artigo anterior, e desejamos prever as mudanças no intervalo de barras de preço. Decidimos usar um classificador de aumento de gradiente para essa tarefa. Para avaliar a importância de cada coluna de dados usando teste de aleatorização, essencialmente treinamos nosso modelo. Ao treinar o classificador de aumento de gradiente usando funções de operador monoidal e configurações de identidade que usamos em nosso artigo anterior, nosso conjunto de dados se assemelhará à tabela abaixo:

Para treinar um classificador de aumento de gradiente usando nosso conjunto de dados, podemos seguir este guia passo a passo com 4 etapas:

Pré-processamento de dados:

Esta etapa começa com a conversão de nossos dados discretos (ou seja, enumerações; período do gráfico de preços, preço aplicado, escolha do indicador, decisão de negociação) em representações numéricas usando técnicas como codificação one-hot. Em seguida, dividimos o conjunto de dados em características (colunas de dados 1-5) e previsões do modelo, além de valores reais (colunas de dados 6-7).

Separação de dados: Após o pré-processamento, precisamos dividir o conjunto de dados em linhas para o conjunto de treinamento e linhas para o conjunto de teste. Isso permite avaliar o desempenho do modelo em dados não vistos, enquanto usamos as configurações que funcionaram melhor em seus dados de treinamento. Normalmente, é usada uma divisão de 80-20, mas você pode ajustar a proporção com base no tamanho e nas características das linhas em seu conjunto de dados. Para as colunas de dados usadas neste artigo, eu recomendaria uma divisão de 60-40.

Criação de um classificador de aprimoramento de gradiente: Em seguida, você inclui bibliotecas necessárias ou implementa funções necessárias para a classificação por aumento de gradiente em C/MQL5. Isso significa incluir nas funções de inicialização do expert as instâncias criadas do modelo de classificador por aumento de gradiente, onde você também especifica hiperparâmetros como número de estimadores, taxa de aprendizado e profundidade máxima.

Modelo de treinamento: Ao iterar sobre os dados de treinamento e variar a ordem de cada coluna de dados durante o processo de tomada de decisão, o conjunto de treinamento é usado para treinar o classificador por aumento de gradiente. Os resultados do modelo são então registrados. Para aumentar a precisão das previsões para ajustes no intervalo de barras de preço, você também pode variar os parâmetros do modelo, como o elemento de identidade de cada monoide ou o tipo de operação (a partir da lista de operações usadas no artigo anterior).

Avaliação do sistema: O modelo seria testado nas linhas de dados de teste (40% separadas na divisão) usando as melhores configurações do treinamento. Isso nos permite determinar quão bem as configurações do modelo treinado funcionam com os dados não treinados. Ao fazer isso, você percorreria todas as linhas de dados no conjunto de dados fora da amostra (linhas de dados de teste) para avaliar a capacidade das melhores configurações do modelo de prever mudanças no intervalo de barras de preço-alvo. Os resultados dos testes podem então ser avaliados usando métodos como o F-score, entre outros.

Você também pode ajustar o modelo se o desempenho precisar de melhorias, alterando os hiperparâmetros do classificador de aumento de gradiente. Para descobrir os melhores hiperparâmetros, você precisaria utilizar métodos como busca em grade e validação cruzada. Depois de desenvolver um modelo bem-sucedido, você pode usá-lo para fazer suposições sobre novos dados não previstos, pré-processando e codificando variáveis categóricas nos novos dados para garantir que tenham o mesmo formato que os dados de treinamento. Com isso, você poderia prever as mudanças no intervalo de barras de preço para novos dados usando o modelo treinado.

Observe que a implementação de classificação por aumento de gradiente em MQL5 pode ser difícil e demorada desde o início. Por isso, o uso de bibliotecas de aprendizado de máquina escritas em C, como XGBoost ou LightGBM, que oferecem implementações eficazes de aumento de gradiente com APIs em C, é altamente recomendado.

Vamos imaginar, para ilustração, que, após permutar nossas colunas de dados, obtemos os seguintes resultados:

• Ao alterar o período da análise retrospectiva, a eficácia da previsão diminui em 0,062.
• O intervalo de tempo para permutação leva a uma redução de desempenho de 0,048.
• A aplicação de permutação ao preço utilizado leva a uma diminuição de desempenho de 0,027.
• A performance diminui em 0,014 ao reorganizar a posição das colunas de dados do indicador.
• A perda de desempenho após a alteração da decisão de negociação resulta em 0,009.

Esses resultados nos levam à conclusão de que o "período de retrospectiva" tem a maior importância em sua posição ao prever mudanças no intervalo de barras de preço, pois permutar seus valores causou a maior redução no desempenho do modelo. O segundo parâmetro mais significativo é o "período", seguido pelo "preço aplicado", "indicador" e, por último, a "decisão de negociação".

Ao quantificar o efeito de cada coluna de dados no desempenho do modelo, esse método nos permite determinar sua relevância relativa. Ao avaliar a importância relativa de cada parâmetro (coluna de dados), estamos mais aptos a escolher parâmetros, projetar parâmetros e talvez até destacar áreas em que nosso modelo de previsão precisa de mais pesquisa e desenvolvimento.

Desse modo, podemos propor ações monoides para o conjunto monoidal de retrospectiva que o alteram adicionando períodos de retrospectiva adicionais que não estão presentes no conjunto monoidal, a fim de explicar ainda mais o aprimoramento. Isso nos permite investigar se esses períodos adicionais têm algum impacto na capacidade de nosso modelo de prever mudanças no intervalo de barras de preço. O conjunto de monoides atualmente consiste em valores de 1 a 8, cada um dos quais é um múltiplo de 4. E se nosso múltiplo fosse 3 ou 2? Que impacto (se houver) isso teria no desempenho? Uma vez que agora compreendemos o lugar do período de retrospectiva no processo de decisão e que ele é o mais sensível para o desempenho geral do sistema, esses e problemas comparáveis podem ser resolvidos.

Valores SHAP

Os valores SHAP (SHapley Additive exPlanations) são um framework unificado que atribui valores de importância a cada coluna de dados com base nos princípios da teoria dos jogos. Os valores SHAP proporcionam uma distribuição justa das contribuições dos parâmetros, considerando todas as possibilidades. Eles oferecem uma compreensão abrangente da importância dos parâmetros em modelos complexos, como XGBoost, LightGBM ou modelos de aprendizado profundo.

Eliminação recursiva de características (RFE)

A RFE é um método iterativo de seleção de características que funciona eliminando recursivamente as características menos importantes com base em seus pesos ou pontuações de importância. O processo continua até que o número desejado de características seja alcançado ou um limite de desempenho seja atingido. Para ilustrar isso, podemos usar um cenário semelhante ao acima, onde temos um conjunto de dados de cinco colunas, do período de retrospectiva ao tipo de decisão de negociação, e queremos prever mudanças no intervalo de barras de preço com base em cada uma das 5 características (colunas de dados). Usamos um classificador de máquina de vetores de suporte (SVM) para esta tarefa. Veja como a eliminação recursiva de recursos (RFE) será aplicada:

• Treinamento do modelo usando um classificador SVM, utilizando todas as colunas de dados no conjunto de dados. Inicialmente, usa-se tudo o que está disponível.
• Em seguida, ocorre a classificação de recursos, onde obtemos pesos ou pontuações de importância atribuídos a cada característica pelo classificador SVM. Isso indica a importância relativa de cada um delas na tarefa de classificação.
• Depois, realiza-se a eliminação da característica menos importante, onde descartamos a coluna de dados menos importante com base nos pesos do SVM. Isso pode ser feito removendo o elemento com o peso mais baixo.
• O modelo é então treinado novamente com colunas de dados reduzidas, em que o classificador SVM é aplicado somente aos recursos restantes.
• A avaliação de desempenho sem a coluna de dados excluída é realizada usando uma métrica de avaliação apropriada, como precisão ou F-score.
• O processo é repetido do passo 2 ao 5 até que o número desejado de colunas, excluindo as características menos importantes (ou colunas de dados), seja alcançado.

Por exemplo, vamos supor que começamos com cinco características e aplicamos a RFE e temos um objetivo de 3 características. Na Iteração 1, vamos supor que esta seja a classificação das características com base nas pontuações de importância decrescentes:

• Período de análise retrospectiva
• Período
• Preço aplicável
• Indicador
• Solução de negociação

Eliminação da característica com a menor pontuação de importância, a decisão de negociação, seria feita. Em seguida, seguiríamos para o retratamento do classificador SVM com as características restantes: período de retrospectiva, período, preço aplicado e indicador. Vamos considerar esta a classificação na iteração 2:

• Período de análise retrospectiva
• Indicador
• Período
• Preço aplicável

Eliminamos a característica com a menor pontuação de importância, que seria o preço aplicado. Uma vez que não restam mais características para eliminar, dado que atingimos o número desejado de características, a iteração seria interrompida. O processo iterativo para, uma vez que alcançamos o número desejado de características (ou outro critério de parada predefinido, como um limite de F-score). O modelo final é, portanto, treinado usando as características selecionadas: período de retrospectiva, indicador e período. A RFE ajuda a identificar as características mais importantes para a tarefa de classificação, eliminando iterativamente as características menos relevantes. Ao selecionar um subconjunto de características que contribuem mais para o desempenho do modelo, a RFE pode melhorar a eficiência do modelo, reduzir o overfitting e aumentar a interpretabilidade.

Regularização L1 (Lasso)

A regularização L1 aplica um termo de penalização à função objetivo do modelo, incentivando pesos de características esparsas. Como resultado, características menos importantes tendem a ter pesos zero ou próximos de zero, permitindo a seleção de características com base na magnitude dos pesos. Considere um cenário em que um trader gostaria de avaliar sua exposição a imóveis e REITs (Real Estate Investment Trusts), e temos um conjunto de dados de preços de imóveis que queremos usar para prever a tendência de preços de casas residenciais com base em várias características, como área, número de quartos, número de banheiros, localização e idade. Podemos usar a Regularização L1, especificamente o algoritmo Lasso, para avaliar a importância dessas características. Veja como funciona:

• Começamos treinando um modelo de regressão linear com regularização L1 (Lasso), usando todas as características no conjunto de dados. A regularização L1 adiciona uma penalização à função objetivo do modelo.
• Após o treinamento do modelo Lasso, obtemos os pesos estimados atribuídos a cada característica. Esses pesos refletem a importância de cada característica na previsão dos preços das casas. A regularização L1 promove pesos esparsos para as características, o que significa que características menos importantes geralmente têm pesos zero ou quase zero.
• Classificação de características: Podemos classificar as características com base na magnitude dos pesos. Características com pesos absolutos mais altos são consideradas mais importantes, enquanto características com pesos próximos a zero são consideradas menos importantes.

Por exemplo, se assumirmos que treinamos um modelo Lasso com o conjunto de dados de preços de imóveis e obtemos os seguintes pesos das características:

• Área: 0,23
• Número de quartos: 0,56
• Número de banheiros: 0,00
• Localização: 0.42
• Idade: 0,09

Com base nesses pesos das características, podemos classificar as características em termos de importância para prever os preços das casas:

• Número de quartos: 0,56
• Localização: 0.42
• Área: 0,23
• Idade: 0,09
• Número de banheiros: 0,00

Neste exemplo, o número de quartos tem o peso absoluto mais alto, indicando que sua importância na previsão dos preços das casas é alta. A localização e a área seguem de perto em importância, enquanto a idade tem um peso relativamente menor. O número de banheiros, neste caso, tem um peso zero, sugerindo que é considerado irrelevante e foi efetivamente excluído do modelo.

Ao aplicar a regularização L1 (Lasso), podemos identificar e selecionar as características mais importantes para prever os preços das casas. A penalização de regularização promove a esparcidade nos pesos das características, permitindo a seleção de características com base na magnitude dos pesos. Essa técnica ajuda a entender quais características têm mais influência na variável-alvo (tendência de preço residencial) e pode ser útil para a engenharia de características, interpretação do modelo e potencial melhoria do desempenho do modelo, reduzindo o overfitting.

Análise de componentes principais (PCA)

PCA é uma técnica de redução de dimensionalidade que pode avaliar indiretamente a importância das características ao transformar as características originais em um espaço de menor dimensionalidade. O PCA identifica direções de máxima variância. Componentes principais com maior variância podem ser considerados mais importantes.

Análise de correlação

A análise de correlação examina a relação linear entre características e a variável-alvo. Características com valores de correlação absoluta mais altos são frequentemente consideradas mais importantes para prever a variável-alvo. No entanto, é importante observar que a correlação não captura relações não lineares.

Informação mútua

A informação mútua mede a dependência estatística entre variáveis. Ela quantifica o quanto de informação sobre uma variável pode ser obtida a partir de outra. Valores mais altos de informação mútua indicam um relacionamento mais forte e podem ser usados para avaliar a importância relativa das características.

Para ilustrar, podemos considerar um cenário em que um trader/investidor está procurando abrir uma posição em uma startup de private equity em ascensão com base em um conjunto de dados de informações do cliente, com o objetivo de prever a perda de clientes com base em várias características disponíveis (nossas colunas de dados) como idade, gênero, renda, tipo de assinatura e compras totais. Podemos usar a Informação Mútua para avaliar a importância dessas características. Veja como funcionaria:

• Começamos calculando a informação mútua entre cada característica e a variável-alvo (rotatividade de clientes). A informação mútua mede a quantidade de informações que uma variável contém sobre a outra. Em nosso caso, ela quantifica a quantidade de informações sobre a rotatividade de clientes que pode ser obtida de cada característica em nossas colunas de dados disponíveis.
• Depois de identificarmos os indicadores de informação mútua, nós os classificamos com base em seus valores. Valores mais altos de informação mútua indicam uma relação mais forte entre a característica e a rotatividade de clientes, sugerindo maior importância.

Por exemplo, se assumirmos que as pontuações de informação mútua para as colunas de dados são:

• Idade: 0,08
• Sexo: 0,03
• Renda: 0,12
• Tipo de assinatura: 0,10
• Total de compras: 0,15

Com base nesses resultados, podemos classificar as características em termos de sua importância para prever a perda de clientes:

• Total de compras: 0,15
• Renda: 0,12
• Tipo de assinatura: 0,10
• Idade: 0,08
• Sexo: 0,03

Neste exemplo, compras totais possui a maior pontuação de informação mútua, indicando que contém a maior quantidade de informação sobre a perda de clientes. Renda e tipo de assinatura seguem de perto, enquanto idade e gênero têm pontuações de informação mútua relativamente mais baixos.

Ao usar a informação mútua, somos capazes de ponderar cada coluna de dados e explorar quais colunas podem ser investigadas ainda mais adicionando ações monoides. Este conjunto de dados é completamente novo, diferente do que tínhamos no artigo anterior, então, para ilustrar, é útil primeiro construir monoides de cada coluna de dados definindo conjuntos respectivos. As compras totais da coluna de dados com supostamente maior informação mútua são dados contínuos e não discretos, o que significa que não podemos aumentar o conjunto monoidal facilmente introduzindo enumerações fora do escopo no monoide base. Desse modo, para estudar mais a fundo ou expandir as compras totais no monoide, poderíamos adicionar a dimensão da data de compra. Isso significa que nosso conjunto de ações terá dados contínuos de data e hora. Ao emparelhar (por meio de ação) com o monoide nas compras totais, para cada compra, poderíamos obter a data da compra, o que nos permitiria explorar a importância das datas e valores das compras na perda de clientes. Isso pode melhorar a precisão das previsões.

Métodos específicos do modelo

Alguns algoritmos de aprendizado de máquina têm métodos específicos para determinar a importância das características. Por exemplo, algoritmos baseados em árvores de decisão podem fornecer pontuações de importância das características com base no número de vezes que uma característica é usada para dividir os dados entre diferentes árvores.

Vamos considerar um cenário em que temos um conjunto de dados de informações do cliente e desejamos prever se um cliente comprará um produto com base em várias características, como idade, gênero, renda e histórico de navegação. Decidimos usar um classificador floresta aleatória para esta tarefa, que é um algoritmo baseado em árvore de decisão. Veja como podemos determinar a importância das características usando este classificador:

• Começamos treinando o classificador floresta aleatória usando todass as características do conjunto de dados. Uma floresta aleatória é um algoritmo de conjunto que combina várias árvores de decisão.
• Após o treinamento do modelo de floresta aleatória, podemos extrair as pontuações de importância do recurso específicas desse algoritmo. As pontuações de importância dos recursos indicam a importância relativa de cada característica em uma tarefa de classificação.
• Em seguida, classificamos as características com base em sua pontuação de importância. As características com pontuações mais altas são consideradas mais importantes porque têm um impacto maior no desempenho do modelo.

Por exemplo, após treinar o classificador floresta aleatória, obtemos os seguintes pontuações de importância das características:

• Idade: 0,28
• Sexo: 0,12
• Renda: 0,34
• Histórico de navegação: 0,46

Com base nesses pontuações de importância das características, podemos classificar as características em termos de sua importância para prever as compras dos clientes:

• Histórico de navegação: 0,46
• Renda: 0,34
• Idade: 0,28
• Sexo: 0,12

Neste exemplo, o histórico de navegação possui a pontuação de importância mais alta, indicando que é a característica mais influente na previsão das compras dos clientes. A renda segue de perto, enquanto a idade e o sexo têm pontuações de importância relativamente mais baixas. Ao aproveitar métodos específicos do algoritmo floresta aleatória, podemos obter pontuações de importância das características com base no número de vezes que cada característica é usada para dividir os dados em diferentes árvores no conjunto. Essas informações nos permitem identificar as características-chave que contribuem de forma mais significativa para a tarefa de previsão. Isso ajuda na seleção de características, na compreensão de padrões subjacentes nos dados e potencialmente na melhoria do desempenho do modelo.

Conhecimento e compreensão da área de estudo

Além de métodos quantitativos, incorporar conhecimento especializado e compreensão da área de estudo é crucial para avaliar a importância das características. Especialistas no assunto podem sempre fornecer insights sobre a relevância e a significância de características específicas com base em sua experiência e conhecimento. Também é importante observar que diferentes métodos podem produzir resultados ligeiramente diferentes, e a escolha da técnica pode depender das características específicas do conjunto de dados e do algoritmo de aprendizado de máquina em uso. Geralmente, é recomendável usar várias técnicas para obter uma compreensão abrangente da importância das características.

Implementação

Para implementar a ponderação de nossas colunas de dados/características, usaremos a correlação. Como estamos mantendo as mesmas características que tínhamos no artigo anterior, estaremos comparando a correlação dos valores do conjunto monoidal com as mudanças no intervalo de barras de preços para obter a ponderação de cada coluna de dados. Lembre-se de que cada coluna de dados é um monoide com um conjunto no qual os valores do conjunto são os valores da coluna. Como estamos testando, no início não sabemos se a coluna mais correlacionada deve ser expandida (transformada por ações monoides) ou se deve ser a coluna de dados com menos correlação. Para isso, adicionaremos um parâmetro adicional que ajudará na tomada dessa decisão em várias execuções de teste. Além disso, introduzimos parâmetros globais adicionais para atender às ações monoides.

//+------------------------------------------------------------------+
//|                                                   TrailingCT.mqh |
//|                   Copyright 2009-2013, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Math\Stat\Math.mqh>
#include <Expert\ExpertTrailing.mqh>
#include <ct_9.mqh>
// wizard description start
//+------------------------------------------------------------------+
//| Description of the class                                         |
//| Title=Trailing Stop based on 'Category Theory' monoid-action concepts  |
//| Type=Trailing                                                    |
//| Name=CategoryTheory                                              |
//| ShortName=CT                                                     |
//| Class=CTrailingCT                                                |
//| Page=trailing_ct                                                 |
//|....	
//| Parameter=IndicatorIdentity,int,0, Indicator Identity            |
//| Parameter=DecisionOperation,int,0, Decision Operation            |
//| Parameter=DecisionIdentity,int,0, Decision Identity              |
//| Parameter=CorrelationInverted,bool,false, Correlation Inverted   |
//+------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//| Class CTrailingCT.                                               |
//| Appointment: Class traling stops with 'Category Theory'          |
//|               monoid-action concepts.                            |
//| Derives from class CExpertTrailing.                              |
//+------------------------------------------------------------------+
int                        __LOOKBACKS[8] = {1,2,3,4,5,6,7,8};
ENUM_TIMEFRAMES            __TIMEFRAMES[8] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES[4] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE };
string                     __INDICATORS[2] = { "RSI", "BOLLINGER_BANDS" };
string                     __DECISIONS[2] = { "TREND", "RANGE" };

#define                    __CORR 5
int                        __LOOKBACKS_A[10] = {1,2,3,4,5,6,7,8,9,10};
ENUM_TIMEFRAMES            __TIMEFRAMES_A[10] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES_A[5] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE, PRICE_WEIGHTED };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CTrailingCT : public CExpertTrailing
  {
protected:
   //--- adjusted parameters
   double m_step;                // trailing step
   
   ...
   
   //
   
   CMonoidAction<double,double>  m_lookback_act;
   CMonoidAction<double,double>  m_timeframe_act;
   CMonoidAction<double,double>  m_appliedprice_act;
   
   bool                          m_correlation_inverted;
   
   int                           m_lookback_identity_act;
   int                           m_timeframe_identity_act;
   int                           m_appliedprice_identity_act;
   
   int                           m_source_size;       // Source Size

public:
   //--- methods of setting adjustable parameters
   
   
   
   
... 
   
   void                 CorrelationInverted(bool value)     { m_correlation_inverted=value;                 }
   
   
... 
   
  };

Além disso, as funções 'Operate_X' foram simplificadas para apenas uma função chamada 'Operate'. Além disso, as funções 'Get' para as colunas de dados foram expandidas para acomodar ações monoides e uma sobrecarga para cada uma delas foi adicionada para ajudar na indexação dos respectivos arrays de variáveis globais.

Isso é como estamos desenvolvendo nossa classe de trailing (trailing stop).

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate(CMonoid<double> &M,EOperations &O,int &OutputIndex)
   {
      OutputIndex=-1;
      //
      double _values[];
      ArrayResize(_values,M.Cardinality());ArrayInitialize(_values,0.0);
      //

      
... 
      
      //
      
      if(O==OP_LEAST)
      {
         OutputIndex=0;
         double _least=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_least>_values[i]){ _least=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_MOST)
      {
         OutputIndex=0;
         double _most=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_most<_values[i]){ _most=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_CLOSEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _closest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_closest>fabs(_values[i]-_mean)){ _closest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
      else if(O==OP_FURTHEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _furthest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_furthest<fabs(_values[i]-_mean)){ _furthest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback(CMonoid<double> &M,int &L[])
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      
... 
   
      int _i_out=-1;
      //
      Operate(M,m_lookback_operation,_i_out);
      
      if(_i_out==-1){ return(4); }
      
      return(4*L[_i_out]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(CMonoid<double> &M, ENUM_TIMEFRAMES &T[])
   {
      
... 
      
      int _i_out=-1;
      //
      Operate(M,m_timeframe_operation,_i_out);
      
      if(_i_out==-1){ return(INVALID_HANDLE); }
      
      return(T[_i_out]);
   }

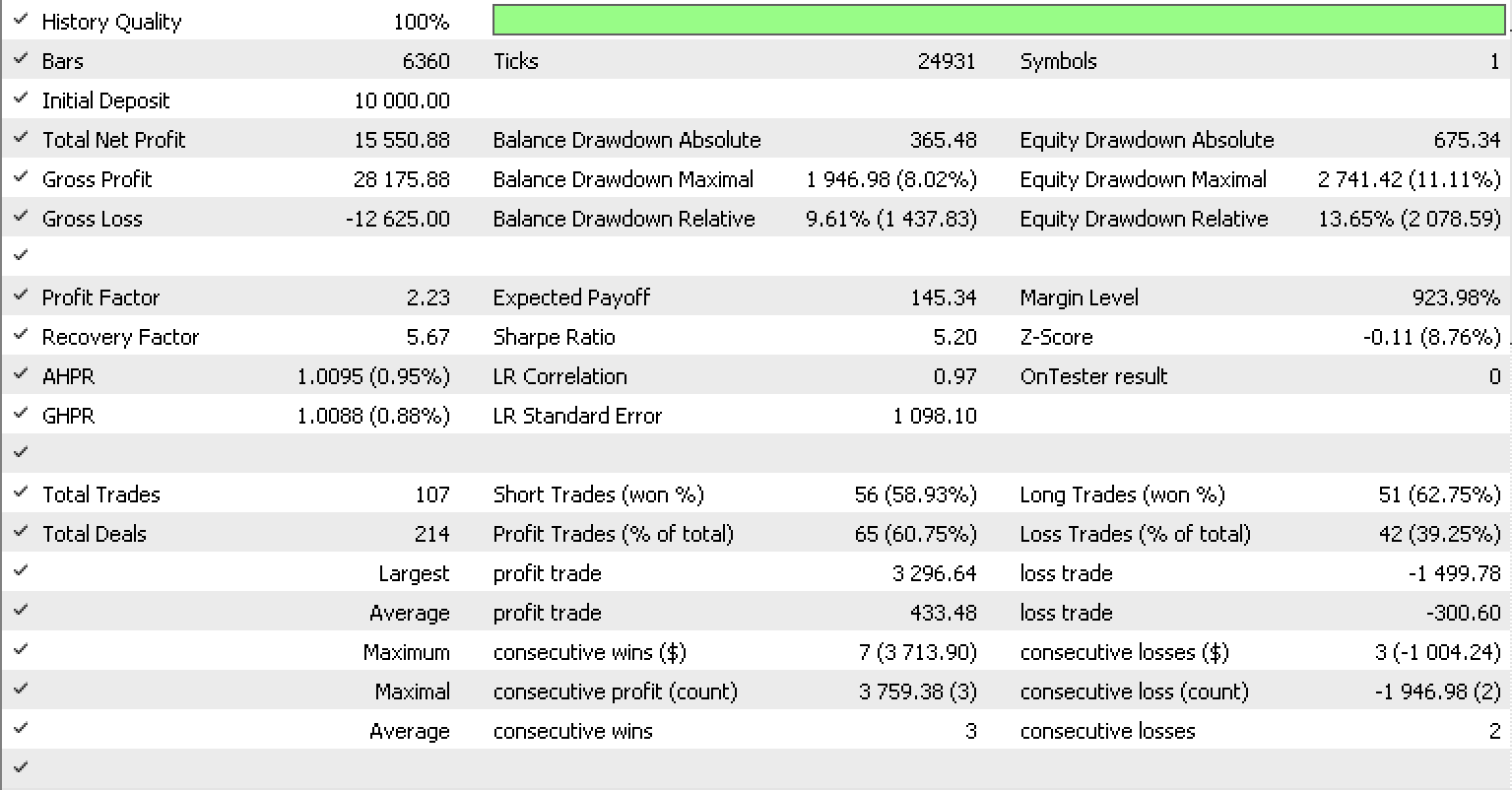
Se executarmos testes como fizemos no artigo anterior para EURUSD no período de uma hora de 01.05.2022 a 15.05.2023, usando a classe de sinal RSI incorporada na biblioteca, este é o nosso relatório de teste.

Conclusão

Em resumo, analisamos como monoides transformados, também conhecidos como ações monoides, podem ajustar ainda mais um sistema de trailing stop que faz previsões sobre volatilidade para ajustar com mais precisão o stop loss de posições abertas. Isso foi analisado em conjunto com vários métodos que são normalmente usados para ponderar as características do modelo (colunas de dados em nosso caso), a fim de entender melhor o modelo, suas sensibilidades e quais características, se houver, precisam ser expandidas para melhorar a precisão do modelo. Obrigado por sua atenção!